基于改进型蚁群算法的输电线路故障测距模型研究

高秉曈，张晨曦，李 红，田怡山，杨 俊

(国网甘肃省电力公司武威供电公司，甘肃 武威 733000)

0 引言

随着我国电力需求的不断增大，电力系统压力与日俱增。输电线路是电力系统的重要组成部分，是发电端与负荷端的连接载体。但是输电线路在运行过程中容易受到外部环境等多种因素的影响，因此已成为电力系统中故障率较高的元件[1-3]。近年来，我国电力系统建设规模不断扩大，因输电线路故障造成的大规模停电事故逐渐增多，对人们正常的生产与生活已经造成了严重干扰。因此，对于输电线路故障测距的研究已经受到了社会各界的广泛关注[4-5]。

随着相关研究工作的不断推进，该问题也取得了一定的研究成果。但是传统故障测距方法精度不高，工作难度大。随着信息与科学技术的不断进步，越来越多的新技术已经广泛应用于输电线路故障测距中，例如各类遗传算法[6]、免疫算法[7]、神经网络算法[8]和蚁群算法[9]等。这些算法能够有效解决故障测距过程中的非线性问题，为故障测距问题的解决提供了新思路。在这些算法中，蚁群算法以其优异的性能脱颖而出。该算法能够将输电线路问题转换为多目标非线性最小化问题，以提升故障测距效果。利用蚁群算法构建不同影响因素约束下的输电线路测距问题的多目标优化模型，可获取精准的故障测距结果。因此，该算法在输电线路故障测距领域的应用具有可行性[10-11]。但由于蚁群算法在计算过程中容易出现停滞的问题，导致算法极容易陷入局部最优，致使故障测距精度有所下降。

为了进一步提高蚁群算法在输电线路故障测距的精度，通过构建改进型蚁群算法的故障测距模型，并利用该模型进行输电线路故障测距，以期获取精度更高的测距结果，使其满足输电线路故障测距的应用要求。

1 改进型蚁群算法

蚂蚁会在爬行路径上留下信息素，使后续蚂蚁以遗留下来的信息素为基础，并通过伪随机比例来选择其移动路径。蚁群算法通过结合精英机制进行信息素更新与传递，以构建一种正反馈机制。利用此方式可获取非线性问题的最优解。在该算法执行过程中，状态行为数据的存储是依靠具备记忆的人工蚂蚁实现的。这些蚂蚁会在特定时刻释放信息素，并在此基础上通过遍历所有路径，以获取最优的移动线路。

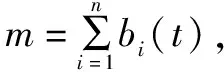
(1)

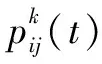
当蚂蚁完成一个路径遍历任务后，将会对信息素进行更新，如式(2)所示：

(2)

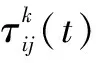
2 故障测距模型

在输电线路运行过程中，三相线路会存在一种互感作用。这种互感作用会对输电线路故障测量精度造成一定的不利影响，因此需要对其进行解耦处理。由于输电线路的各个参数具有非线性，需要针对模型参数的阻抗矩阵和采纳矩阵获得输电线路系统的相模矩阵S。其中，相模矩阵变化与反变化如式(3)所示。

(3)

式中：S为相模矩阵；Q为反变换后的相模矩阵，S-1=QT；a、b、c为输电线路所代表的三相；m1、m2、m3为输电线路发生故障时，电力系统存在的1模、2模、3模分量；U为电压；I为电流。

因此，对电力系统参数进行模变处理后，可以获取电力系统任意一个分量值，表示为式(4)和式(5)：

Ux=U1cosh(γx)-ZcI1sinh(γx)

(4)

(5)

式中：γ为输电线路传播参数；Ux为距离始端x处的电压；Ix为距离始端x处的电流；Zc为波阻抗；U1为1模分量电压；I1为1模分量电流。

在输电线路发生任意故障时，电力系统会存在1模分量。在实际工况中，输电线路发电端m与负荷端n的数据是异步的，但是这两端的电压幅值相等，如式(6)所示。

(6)

式中：UFm1、UFn1分别为m、n端计算得到的故障点过渡电阻的电压。

在利用蚁群算法构建输电线路故障测距模型的过程中，输电线路会存在较多的谐波。谐波分量会导致测距精度下降。因此，本文采用傅氏补偿滤波法对谐波进行滤波处理。滤波处理后，式(6)可以转换为式(7)：

(7)

式中：Um1、Un1分别为m、n端计算得到的1模分量电压；Im1、In1分别为m、n端计算得到的1模分量电流。

对Dmf参数进行归一化处理，将改值控制在[0,1]区间范围内，则线路的总长为1。在此基础上，将故障测距问题转换为多目标非线性最小化问题，以此获得测量模型的最优解，如式(8)所示：

(8)

式中：a=real[Z1(x)]；b=imag[Z1(x)]；c=real[Z2(x)]；d=imag[Z2(x)]。

3 试验分析

以雷电常发环境下的750 kV超高压输电线路为研究对象，进行仿真试验。该试验运用交替顺态程序-电磁暂态程序(alternative transients program-electromagnetic transients program,ATP-EMTP)构建输电线路模型，并采用MATLAB软件进行算法编程。

3.1 模型构建和波形选择

试验所选择的输电线路总长为500 km，单位正序阻抗值为(0.012 7+j0.268)Ω/km，线路正序阻抗为(0.012 7+j0.268)Ω/km，零序阻抗值为(0.272 9+j0.84)Ω/km，正序分布电容为(-81.367 ×10)F/km；发电端m的正序阻抗为(0.725+j40.24)Ω，负荷端n的正序阻抗为(2.341+j134.13)Ω，发电端m与负荷端n的电压幅角相位角相差30°。

在发电端m和负荷端n均布置电流测量装置，通过装设路线开关以便进行输电线路相间短路的故障模拟，并对故障参数进行收集和分析。ATP-EMTP故障仿真模型如图1所示。

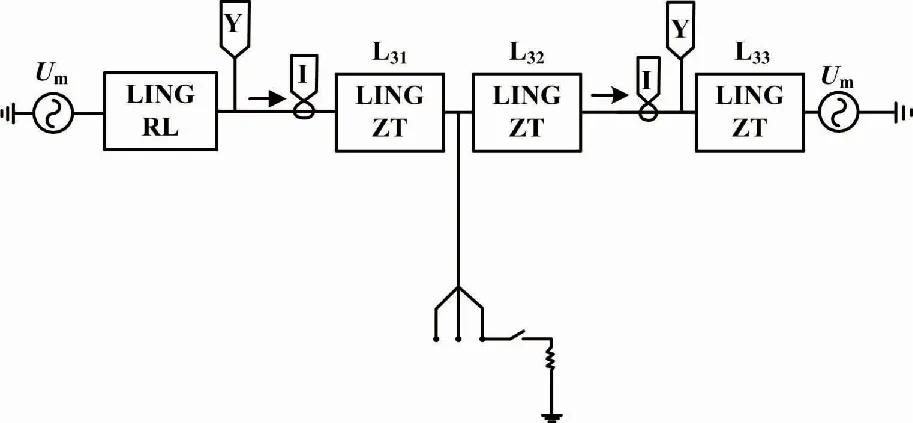
图1 ATP-EMTP故障仿真模型

在该模型中，分别对输电线路各种典型故障进行了设计，如单相短路、两相接地、相间短路、三相短路。

3.2 算法的仿真分析

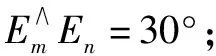
3.2.1 过渡电阻的影响

设定超高压输电线路的故障距离为220 km，获得不同故障电阻下故障距离的相对误差。不同故障电阻下的仿真结果如表1所示。表1中的过渡电阻主要是指相接地电阻或短路过渡电阻。分析表1可知，本文模型的输电电路故障距离测算的相对误差均在0.1%以内，说明该模型的计算误差低，能够得到更为精准的超高压输电线路故障测距结果。

表1 不同故障电阻下的仿真结果

在上述试验的基础上，对本文所设计模型进行不同故障点下的故障测距。不同故障点下的仿真结果如表2所示。

表2 不同故障点下的仿真结果

分析表2可知，在不同故障点下，超高压输电线路短路距离对试验结果精度的影响不大，表明该模型基本不受短路距离的影响。

3.2.2 不同步角的影响

不同步角是指线路两端数据不以相同参考相量为基础。A-G故障下不同步角的仿真结果如表3所示。

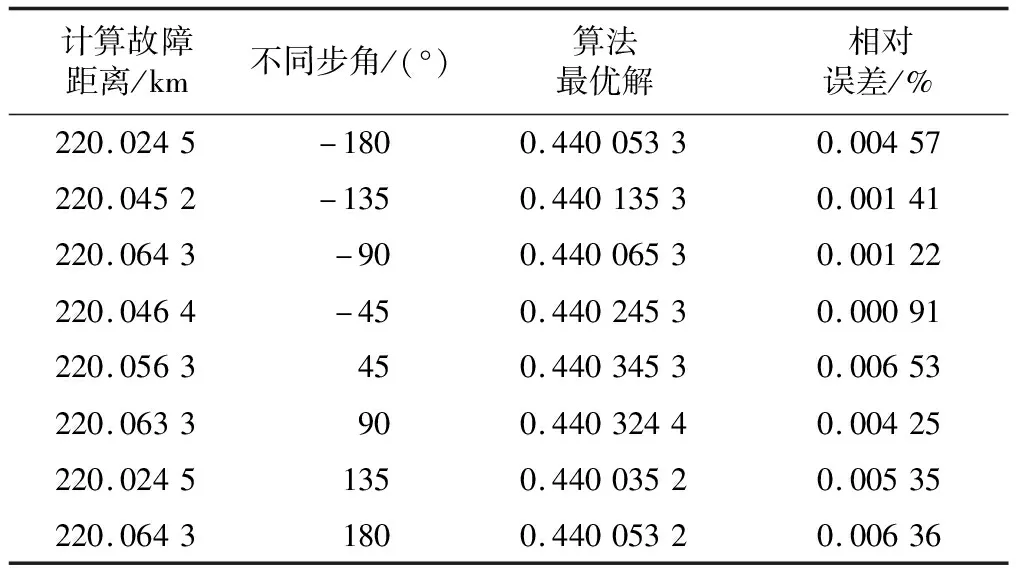
表3 A-G故障下不同步角的仿真结果

在步角不断变化情况下，输电线路测距的相对误差也存在较大变化。当步角为45°时，相对误差达到最高值0.006 53%，之后逐步下降；当步角达到90°后，相对误差逐渐上升，说明步角对超高压输电线路测距结果具有较大影响。

3.2.3 不同模型下的仿真结果

为了进一步验证本文模型故障测距精度，采用文献[2]模型和文献[3]模型与本文模型进行对比分析。不同模型下的仿真结果如表4所示。由表4可知：文献[2]模型下的超高压输电线路故障测距的最高相对误差为0.211%；文献[3]模型下的最高相对误差为0.388%；本文模型的最高相对误差为0.051%。结果表明，本文模型的故障测距相对误差最小，验证了本文模型的优越性。这是由于基于改进型蚁群算法的本文模型能够更为真实地反映故障位置情况。因此，本文模型具有较低的故障测距误差与较高的测距精度。

表4 不同模型下的仿真结果

4 结论

随着社会用电需求的逐步扩大，超高压输电线路故障事件数量逐渐升高，因此需要利用相关的输电线路测距技术，及时进行故障位置定位、提升线路的维修与维护效率、降低巡检难度，以保证电力系统的安全稳定运行。因此，本文通过引入改进型蚁群算法，构建输电线路故障测距模型，将故障测距问题转换为非线性目标函数求解问题，并利用改进型蚁群算法进行模型求解，以获取故障测距结果的最优解。本文结论如下。

①本文通过构建一种基于改进型蚁群算法的输电线路故障测距模型，并采用相模变换和傅氏补偿算法相结合的方法减少其他因素对测距结果的影响，以降低测距结果的相对误差、提升测距精度。

②本文采用MATLAB 软件对该模型进行了仿真分析。仿真测试结果表明，该模型受到的外界因素影响较小，对不同类型的故障测距都可以获得高精度的测距结果，可以在电力系统中进行大力推广与应用，从而保证供电安全与电力系统的安全、稳定运行。