基于有偏卡尔曼的多传感器数据融合研究

2022-02-25岳元龙陈亚南

仪表技术与传感器 2022年1期

岳元龙，陈亚南，孙钦，左信

(1.中国石油大学(北京)自动化系，北京 102249；2.中海石油(中国)有限公司北京研究中心，北京 100028)

0 引言

随着电子信息技术的发展，各种面向复杂应用系统的多传感器数据融合系统大量出现，需要对多种传感器和不同信息源进行更有效的集成，以提高数据处理的自动化程度[1]。单传感器测量的数据往往具有不完整性和不确定性，因此多传感器数据融合逐渐成为国内外专家研究的焦点[2]，并在目标识别、图像处理、故障诊断等方面得到广泛的应用。近些年各种数据融合算法得到广泛研究，其中最具代表的是卡尔曼滤波算法。卡尔曼是一种线性无偏最小均方误差估计，它只能保证在整个线性无偏估计类中是最优的，但并不能保证在整个线性估计中仍是最优的[3]。有偏卡尔曼可以通过引入偏差进一步降低卡尔曼的估计均方误差[4-5]。目前关于有偏卡尔曼滤波算法的研究比较少，虽然文献[6]给出了有偏卡尔曼的构造思想，或者只给出了某一时刻卡尔曼的有偏算法而没考虑有偏卡尔曼滤波的迭代过程[7]。本文基于统一有偏估计思想，推导出完整的有偏卡尔曼滤波过程，然后将有偏卡尔曼分别与扩维融合和序贯融合相结合，提出扩维有偏卡尔曼滤波和序贯有偏卡尔曼滤波，进一步提高多传感器数据融合精度。

1 卡尔曼滤波算法

考虑单传感器状态方程和测量方程为：

xk=Fkxk-1+wk

(1)

zk=Hkxk+vk

(2)

式中：k为离散时间变量，k≥0；xk为状态向量，xk∈Rnx×1；Hk为观测矩阵，Hk∈Rp×nx；wk为系统噪声，wk∈Rnx×1，满足wk∈N(0,Qk)；Qk为系统噪声的协方差矩阵，Qk∈Rnx×nx；vk为观测噪声，vk∈Rp×1，满足vk∈N(0,Rk)；Rk为观测噪声的协方差矩阵，Rk∈Rp×p。

传统的卡尔曼滤波模型为[8]：

(3)

(4)

(5)

(6)

(7)

2 有偏卡尔曼滤波算法

通过偏置最小无偏均方误差估计卡尔曼滤波的输出结果，便可得到在均方误差条件下优于传统卡尔曼的有偏卡尔曼滤波[8]。有偏卡尔曼滤波的定义如下：

(8)

式中γ称为偏参数。

文献[7]推导出了偏参数是单变量形式的BKF，本文把偏参数扩展到矩阵范围，推导出偏参数是矩阵形式的BKF。矩阵形式的有偏卡尔曼定义为

(9)

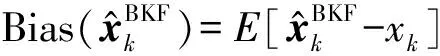
=(Mk-I)xk

(10)

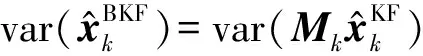
(11)

那么偏参数为矩阵形式的BKF的均方误差(MSE)可以表示为

(12)

(13)

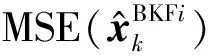
(14)

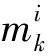
(15)

将式(15)代入式(13)得：

(16)

即偏参数取最优时，在均方误差条件下BKF要优于KF。偏参数为矩阵形式的BKF完整公式为：

3 扩维和序贯有偏卡尔曼滤波算法

3.1 扩维有偏卡尔曼滤波

考虑N个传感器以相同的采样速率对系统进行观测。系统的测量方程为

(17)

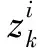
扩维融合的基本思路是将各传感器的观测值经过扩维处理组成一个新的观测量[10]。扩维有偏卡尔曼滤波算法流程如图1所示。

图1 扩维有偏卡尔曼滤波

将所有的传感器的量测写成扩维向量的形式，即：

(18)

(19)

(20)

扩维后的测量噪声方差为

(21)

新的观测方程为

zk=Hkxk+wk

(22)

因此，式(1)和式(22)组成了一个新的系统，再利用BKF算法便可得到扩维BKF融合估计器。扩维BKF的计算过程中涉及到矩阵求逆运算，该类运算的时间复杂度随着矩阵维数增加而呈指数增长，当融合中心传感器数量较多时，时间复杂度会急剧增大，影响了中心处理器的的执行速度，降低了算法的实用性。

3.2 序贯有偏卡尔曼滤波

图2 序贯有偏卡尔曼滤波示意图

(23)

(24)

再用N个传感器进行循环更新处理，其中，第j个传感器的估计值和方差矩阵为：

j=1,2,…,N

(25)

(26)

完整的序贯BKF算法为：

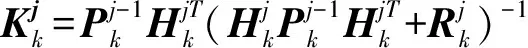
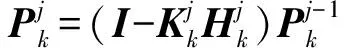
j=1,2，…，N

3.3 扩维BKF和序贯BKF的精度比较

KF扩维融合估计均方误差矩阵的Fisher信息形式可以写为

(27)

同理BKF扩维融合估计误差协方差矩阵的Fisher信息形式可以写为：

(28)

可以用归纳法得到序贯BKF融合k+1时刻的状态估计及其均方误差矩阵为：

(29)

(30)

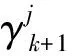
4 算例与分析

算例1是以单传感器为例验证有偏卡尔曼在均方误差条件下优于传统的卡尔曼滤波，假设线性系统状态转移矩阵为

(31)

观测矩阵为

Hk=[1 1 1 1 1]

(32)

图3 BKF和KF的均方误差比较

表1 2种算法的均方误差表

由图3可以看出，在均方误差条件下BKF要优于KF。由表1可以看出，随着观测噪声增大，BKF与KF的NMSE相差越大，也即BKF的优势越突出。

算例2中，为方便描述，选择状态转移矩阵为

(33)

5个观测器的观测矩阵分别为：

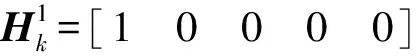
(34)

观测量为

(35)

图4 4种估计的均方误差比较

表2 仿真运行时间和均方误差表

观察图4和表2可以得出以下结论：

(1)从图4可以看出扩维KF和序贯KF的均方误差要大于扩维BKF和序贯BKF，说明前两者的滤波结果与真实值相比有较大偏差，受系统测量误差影响较大，后两者均方误差较小，滤波结果与真实值较为接近，即扩维BKF和序贯BKF能够有效消除系统误差，提高融合精度。

(2)从表2中各算法NMSE的标准差可以看出，扩维BKF和序贯BKF的NMSE的标准差比较小，即滤波结果的NMSE波动比较小，误差表现比较平稳。而扩维KF和序贯KF的NMSE的标准差比较大。相比之下，在多传感器的情况下，扩维BKF和序贯BKF能够获得更高的状态估计精度，能够消除未知系统误差对其造成的影响。

(3)从图4可以看出，序贯BKF的均方误差要优于扩维BKF的均方误差，即对于多传感器来说，序贯BKF要优于扩维BKF。

(4)从表2中各种算法的平均运行时间可以看出，时间复杂度从高到低分别是序贯BKF、序贯KF、扩维BKF、扩维KF，由于滤波算法中存在矩阵求逆，所以随着系统维数增加，扩维融合和序贯融合算法之间的时间复杂度关系会发生变化。