国外某桥梁工程坐标系建立的过程分析
2022-02-25陈军
陈 军
(天津市政工程设计研究总院有限公司,天津市 300201)
0 引 言
随着“一带一路”相关工程项目的迅猛推进,沿线许多大型基建项目已开工建设,特别是南亚地区的基建项目已遍地开花,给当地人民带来福祉。在许多这些项目所处的国家都使用了UTM投影作为本国基础地形图的投影方式,但对于建设精度要求较高、线路较长的大型工程,若后续所有建设的坐标基准仍采用UTM投影方式建立,则能否满足我国《公路勘测规范》(以下简称《规范》)中对坐标系投影长度变形的要求,从而影响到整个工程的建设精度,是测量任务实施前必须要考虑的问题。因此,按照工程所处的地理位置,选取合理的地图投影方式建立工程坐标系统,已成为此类工程建设的关键一环。
1 国外某桥梁工程介绍
南亚某国新建大型高架公路工程,全线均采用高架桥设计,路线全长约35km,东西方向长约23km,工程所处区域中部经度为90°17’,平均海拔约8m,属冲积平原。工程可行性研究阶段的地形图资料显示,其使用的是WGS84椭球下的UTM46N投影坐标系,中央子午线为93°。本工程属于大型连续多跨桥梁,按照《规范》要求,工程所采用的平面控制测量坐标系投影长度变形值不应大于10mm/km,因此,必须根据工程的实际情况分析原有坐标系的适用性。
2 UTM投影变形分析
UTM(UniversalTransverseMercator)投影由美国军事测绘局于20世纪40年代提出,是等角横轴割圆柱投影,椭圆柱分别割地球于南纬80°和北纬84°,投影后两条割线不产生变形,它们距离6°带的中央子午线约180km;投影后两条割线以内长度缩小,以外长度变大,中央子午线的投影长度比为0.9996。
根据投影变形值计算公式:
式中:S为椭球上大地线长度;m为长度比;yU为大地线两端点横坐标平均值;R为大地线所处位置的平均曲率半径。
式(1)中设定S为1000m,m为0.9996,即可计算UTM投影的变形曲线,见图1。
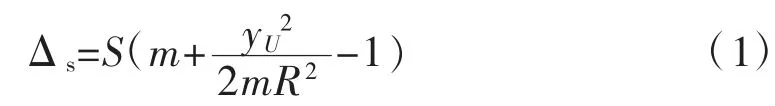

图1 UTM投影变形曲线图
由图1可以看出,采用UTM投影,椭球面上距中央子午线180km范围内投影后长度缩短,180km以外投影后长度增大,且增大的速率逐渐加快。
本工程所在区域中部距UTM46N投影带中央子午线约275km,结合图1的UTM投影变形曲线图可以看出,若工程采用UTM46N投影,则其产生的投影变形值将达到520mm/km,这已远远超过了《规范》的允许值。因此,为保证此工程在测量、设计和施工期间所采用的坐标系投影变形值最小,满足工程建设的精度要求,必须建立适合工程需求的工程坐标系。
3 工程坐标系的建立
横轴墨卡托(TransverseMercator)投影是等角横轴切圆柱投影,圆柱面与经线相切,其投影后中央子午线不产生变形,投影长度比为1,距中央子午线越远投影变形越大,是我国工程中普遍采用的投影方式。将式(1)中的m设定为1,则得到横轴墨卡托投影变形值计算公式(2)。

式中:S为椭球上大地线长度;yT为大地线两端点横坐标平均值;R为大地线所处位置的平均曲率半径。同样,设定S为1000m,则可以得到横轴墨卡托投影的变形值,见图2。

图2 横轴墨卡托投影变形曲线图
从图2可以看出,距横轴墨卡托投影中央子午线东西方向共57km范围内,其投影变形值小于10mm/km,在90km范围内,其投影变形值小于25mm/km。本工程东西方向长23km,若采用横轴墨卡托投影,将工程中部位置经线设定为中央子午线,则在工程范围内的横轴墨卡托投影变形值在《规范》的允许值内。
此外,还要考虑地面水平距离投影到椭球面的长度变形,此变形值可根据式(3)进行计算。

式中:S0为地面水平距离;Hm为地面边长两端的平均高程;hm为投影面高程;Rm为大地线所处位置的平均曲率半径。
综合考虑上述两种投影变形的影响,设定工程坐标系的中央子午线为工程中部的90°17’,投影面高程为零,工程沿线高程值在6~11m之间,则经过计算后,在工程区域内的综合投影长度变形值完全小于10mm/km(见表3),满足《规范》中对大型构造物平面控制测量坐标系投影长度变形值的限差要求。

表3 综合投影长度变形值计算表
4 坐标系间的转换

建立工程坐标系后,还应考虑与UTM投影坐标系的坐标转换,以便将工程相关图纸转换到UTM坐标系后,移交当地土地管理或规划部门使用。因为两种坐标系的参考椭球都为WGS84椭球,所以坐标转换的实质为坐标系A到WGS84椭球下的大地坐标,再由WGS84椭球下的大地坐标到坐标系B的转换,即等角横轴圆柱投影的坐标正反算,其公式分别为正算公式(4)和反算公式(5):
式(4)和式(5)中:(x,y)为投影后的平面坐标;(B,L)为WGS84椭球下的大地坐标;m为长度比;函数F1和F2为坐标正算的投影函数;函数F3和F4为坐标反算的投影函数。
由工程坐标转换为UTM投影坐标时,先利用式(5),将m设定为1,将横轴墨卡托投影下的平面坐标(xT,yT)转换为大地坐标(B,L);然后再利用式(4),将m设定为0.9996,将大地坐标(B,L)转换为UTM投影坐标(xU,yU)。同理,如果由UTM坐标转换为工程坐标,则式(5)中的m设定为0.9996,式(4)中的m设定为1,投影函数不变。
上述转换过程可以利用专业的坐标转换软件进行,但是每次转换时都需要输入相应的转换参数,且转换时需要过渡到大地坐标才能进行,操作极为不便。因此,可以根据上述转换公式和过程,把两种坐标相互转换的参数固定,利用C#等编程语言将转换过程程序化,生成方便实用的坐标转换界面(见图3),提高转换效率。
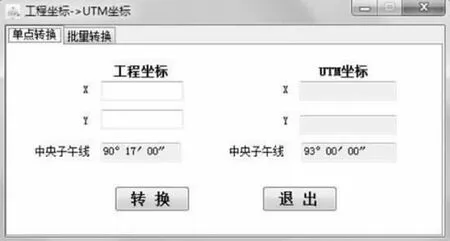
图3 坐标转换软件界面
5 结语
根据国外工程建设情况和工程所处的地理位置,考虑所在地区基础测绘所采用的坐标系统,因地制宜,建立满足工程精度要求的坐标系统,是工程测量实施前必须考虑的重要内容。只有综合考虑工程所处区域情况以及所采用坐标系统的投影长度变形值大小,选择最优的参考椭球和投影方式,建立满足规范要求的工程坐标系统,才能保证工程在测绘、设计和施工等各个阶段的工作顺利开展,为工程的高质量建设打下良好基础。
