高墩大跨曲线连续刚构桥的概念设计

何文杰

（中交公路规划设计院有限公司，北京市 100088）

0 引 言

结构设计和结构分析是2种概念，应区别看待。随着计算机硬件的飞速发展和大型有限元分析程序的普及应用，许多桥梁工程师过多依赖于计算机程序进行结构计算，而忽视了专业设计的能力。而概念设计是设计理论研究和应用实践相结合的第一步。

桥梁概念设计是指结合工程经验，从宏观层面上综合考虑人文、地理、美学、功能、交通、经济、结构性能、材料性能、防灾和耐久性等因素，初步确定相对合理的结构设计方案，基本满足预定的设计原则[1]。

本文结合新疆维吾尔自治区乌鲁木齐市郊外某高速公路上1座高墩大跨曲线预应力混凝土连续刚构桥的设计，从多个角度阐述了概念设计的关键理念和实用方法。

1 工程概况

本项目道路等级为一级公路，路基宽度19m，双向4车道，设计车速100km/h。桥址位于宽阔峡谷地带，属严寒气候地区，环境类别为Ⅱ类（冻融环境），基本风速37.3m/s。抗震设防烈度为Ⅷ度，动峰值加速度0.2g（地震安评报告取0.3g），特征周期0.4s，Ⅱ类场地。地质岩土主要为全、中风化泥质砂岩。

拟设计1座桥梁跨越山谷，一端连接既有城市主干道，另一端连接主线区互通，实现城区道路与环线高速衔接的交通功能。

2 平面线形

路线线位应根据现场自然条件及地物、人为因素障碍情况来优化确定，并选择相应技术标准。

本地区上跨宽阔峡谷，被连接的两端直线距离约2.3km，路线中段约500m范围内高程变化较小，两侧高程变化较大。地面控制因素有河流、水渠、厂房、燃气管道、高压线和混凝土道路等。经过与地方负责单位沟通，为有效避让厂房并尽量使设计路线与被交道路、河流、水渠、管道和高压线正交，最终将路线平面设计为曲线形，平曲线半径为1600m，总长约2.4km。

路线平面及地形示意图见图1。

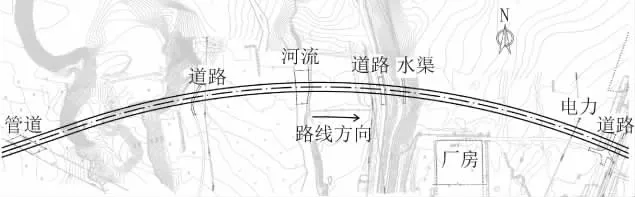
图1 路线平面及地形示意

3 桥梁结构类型

根据路线平面及纵断高程，路线中段约500m范围内地形较为平坦，桥梁高度约85~130m，之外的桥高约5~85m。因此，初步确定主桥主跨范围总长不小于500m，主桥两侧均为引桥。根据工程经验，主桥范围的桥跨应大于100m，否则下部造价占比高，综合经济性差。高墩大跨曲线桥对上部梁体抗扭能力有较高要求，适合此条件的桥型有上承式拱桥、斜拉桥和连续刚构桥。

（1）拱桥。拱桥是力与美的结合体。上承式拱桥适用于桥下空间充足的区域，通过腹杆将桥面荷载传递至拱肋，由于拱脚推力的存在，大大降低了拱肋的弯矩。但平面曲线桥的倾覆力矩限制了拱桥的跨径，且拱桥基础存在较大水平推力，对地质条件要求高。本桥桩基持力层的岩饱和单轴抗压强度5MPa，岩层埋置较深。因此，拱桥不作佳选。

（2）斜拉桥。斜拉桥通过倾斜的拉索将桥面荷载及主梁自重传递至桥塔上，最终由受压的塔身、受拉的拉索、受压弯的主梁和桥墩组成结构受力体系。本桥为曲线桥，斜拉桥的拉索力会对主梁产生较大的轴力和曲线向心力，为提高主梁刚度，需设计较大的截面尺寸。主梁若采用钢梁则造价过高，超出投资方限制，若采用混凝土梁则梁体自重会产生较大的地震效应力。因此，斜拉桥不作佳选。

（3）刚构桥。刚构桥是指梁和桥墩固结形成刚性连接，承重采用刚架结构的桥梁。刚构桥桥墩能承担竖向压力、弯矩和水平推力，从而减小了主梁弯矩，其跨越能力大于普通梁桥。墩梁固结增强了刚构桥的整体稳定性和抗震能力，与其他高强材料对比，混凝土和钢筋的材料单价低，经济性好。

因此，本项目主桥结构优选预应力混凝土连续刚构桥。

4 跨径及美观

一座优雅美观的桥梁，备受人们喜爱，不可低估其艺术价值对社会价值的影响。在概念设计阶段，桥梁设计应兼顾结构和美观的需求[2]。

（1）视觉美。电影是一种视觉艺术，它通过银幕展现给观众美丽的画面和感性氛围。标准的屏幕比例一般有4∶3和16∶9两种，抛开数码技术不谈，后者称为宽屏。接近黄金分割比例的宽屏已占领主要市场，因为人的眼睛更喜欢宽屏带来的视觉体验。本桥处于空旷较宽峡谷内，视野通透性好，高墩长联桥的总体景观性可参考以上所述的画面比例法设计。主跨区的桥梁高度约85~130m，减去主梁高度，墩高约80~120m。将单跨的两侧桥墩视为屏幕短边，上部主梁视为屏幕长边，按16∶9的比例计算，对应单跨跨径为142~213m。

（2）功能。桥址处的地面控制性因素有河流、水渠、被交路和管线等，桥梁布跨时，桥墩及承台需满足相关障碍物的水平净距要求。结合地面实测数据，在满足净距要求前提下，主跨区可采用2跨300m、3跨200m、4跨150m和5跨120m4种跨径方案。

（3）安全经济。本桥平面曲线半径1600m，以单跨为研究对象，跨径两侧的梁端截面中心之间的弦线与实际平面曲线之间的偏心距，由梁端向跨中逐渐增大。同时，随着跨径的增加，梁体自重产生的面外倾覆弯矩也逐步增大，从而影响桥梁的整体稳定安全性。根据估算结果，跨径大于150m时，倾覆弯矩过大，这将增加下部结构负担和造价比例。各种跨径的主梁轴线最大偏心距及面外倾覆弯矩估算值见表1。

表1 主梁轴线最大偏心距及面外倾覆弯矩

根据以上分析结论，主桥桥跨布置采用82m+4×150m+82m，基本满足视觉美观、功能和安全性。跨径立面示意图见图2。

图2 跨径立面示意图（单位：m）

5 上部结构

5.1 梁高

公路桥的变截面梁高可根据高跨比h/L来拟定，最小梁高hmin取（1/30~1/50）L，最大梁高hmax取（1/16~1/25）L，最大梁高与最小梁高比值hmax/hmin取2.0~3.0。按此原则，本桥最小梁高取3.5m，最大梁高取9.0m。

5.2 梁截面

本桥整幅宽19m，由以上第3节结论，主梁优选箱型断面（有利于抗扭）。初拟采用直腹板箱梁，箱梁翼缘板悬臂长4m，梁底宽11m，采用单箱双室型断面。单箱双室直腹梁断面示意图见图3。

图3 单箱双室直腹梁断面示意图（单位：cm）

参考全国桥梁抗风风险区划图，桥址位于R1区，重现期100a的基本风速是37.3m/s。由工程经验可知，此风速可能控制下部结构静力验算，因此，应采取措施减小由上部箱梁引起的风荷载效应。根据《公路桥梁抗风设计规范》（JTG/T3360-01—2018），主梁风荷载Fg计算公式为：

式中：ρ为空气密度；Ug为等效静阵风风速；CH为横向力系数；D为主梁特征高度，ηc为腹板倾角角度折减系数；βd为斜腹板倾角[3]。

当主梁截面带有斜腹板时，横向力系数可根据腹板倾角角度折减，采用CH·ηc。

由式（1）、式（2）可知，将箱梁的直腹板改为斜腹板设计，可减小风荷载效应值，减小的幅度与斜腹板倾角相关。

单箱双室斜腹板箱梁断面示意图见图4。

图4 单箱双室斜腹梁断面示意图（单位：cm）

相对于直腹梁而言，采用斜腹梁方案除能减小风荷载效应外，也能减小由箱梁自重引起的水平地震作用效应，并节省约2000m3混凝土。但对于斜腹梁方案，纵桥向的梁高呈2次抛物线变化，横桥向的底板宽呈线形变化，且桥型平面位于平曲线上。高空施工作业时，三维空间定位难度大，施工质量难以保证。因此，在满足结构计算要求的前提下，优先考虑直腹梁截面方案。

5.3 梁段划分

采用挂篮悬浇法施工时，需要将梁体划分成多个节段，此时应综合考虑设计和施工因素。

从设计角度看，每个梁段长度取2.5~5.0m，能满足计算要求。靠近主墩的梁高较大，梁段长度取小值，远离主墩的梁高较小，梁段长度取大值，使得每个梁段重量相对均衡，避免悬臂阶段钢束应力相差较大，减少了预应力型号。

从施工角度看，应考虑挂篮承载吨位和施工周期的影响。本桥位于严寒气候地区，一年之中，仅4月至10月（约210d）期间的气温宜施工，施工连续作业周期短。因此，应尽量加大单梁段长度，减少梁段数量，在1a内完成主梁合拢，避免主梁大悬臂状态过冬带来的施工风险。本桥按整幅设计，梁段每延米的自重大，单个梁段的重量应同时考虑施工设备的限制条件。

经过对比分析，本桥最终采用单个长度为3.5m、4.0m和5.0m的梁段组合方案，主墩单侧悬臂共划分成16个梁段，最大块段质量310t，满足施工设备要求。按12d/段的悬臂施工速度计算，悬臂梁段总工期为16×12=192d，满足施工期要求。

6 下部结构

高墩大跨连续刚构桥的下部结构往往成为结构设计难点，如何在设计初期阶段确定墩身的相关计算参数及截面形状和基本尺寸，对整个桥梁后续设计至关重要。

6.1 二阶效应

结构的二阶效应包括整体层面的重力二阶效应（P-Δ效应）和构件层面的受压构件挠曲效应（P-δ效应）两部分，其示意图见图5、图6。

图5 P-Δ效应

图6 P-δ效应

当偏心受压构件的P-Δ效应使作用显著增大而不可忽略时（一般认为结构在水平荷载作用下的重力附加弯矩大于初始弯矩的10%时），在分析中应考虑其不利影响，计算中可不考虑杆件的扭曲变形。实际工程中，可采用有限元分析法或按采用弯矩增大系数的简化方法来实现。在设计操作层面，根据总体计算模型查询重力附加弯矩占比来判断是否考虑其影响，或在输入程序参数时勾选考虑P-Δ效应并关联对应的竖向荷载工况。

偏心受压构件在竖向荷载作用下由P-δ效应引起的二阶弯矩，可采用偏心距增大系数η与构件计算长度L0相结合的方法进行简化计算。

当偏心受压构件的长细比17.5＜L0/r＜70（r为截面绕计算轴的回转半径），其正截面承载力计算应考虑构件挠曲二阶效应引起的附加内力（当L0/r＞70时，破坏形态为弹性失稳）。计算时，可将轴力对截面形心的初始偏心距ei乘以偏心距增大系数η。初始偏心距ei=e0+ea，其中：e0为轴向力设计值Nd对截面重心轴的偏心距，e0=Md/Nd，Md为对应于轴向力设计值Nd且考虑了重力二阶效应（如需考虑）后的截面弯矩设计值；ea为由施工误差或材料缺陷等产生的附加偏心距。

公路桥规在计算偏心受压构件的正截面抗压承载力时，未考虑ea值影响。但在计算偏心距增大系数η时，规定e0不小于20mm和偏压方向截面最大尺寸的1/30，其实质是指e0的下限值不小于ea值。η计算式[4]为：

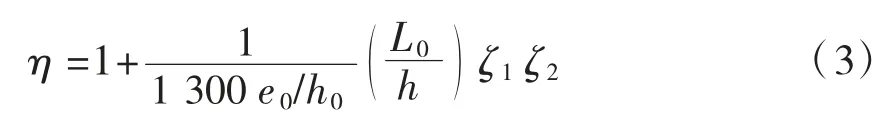
图7 二阶弯矩叠加示意图

6.2 墩身的计算长度

由上述可知，在进行构件的P-δ效应分析时，无论是构件的长细比还是偏心距增大系数，均与构件的计算长度密切相关，且其直接影响构件的截面验算结果。而构件的计算长度L0需根据工程经验或参照相关理论来确定，本文采用经验法、规范法、基于欧拉公式的屈曲分析法。

6.2.1 经验法

受压构件的计算长度L0=μL，其中：L为构件自由长度；μ为计算长度系数。当构件两端均为固定时，μ取0.5；当两端均铰接时，μ取1.0；当一端固定另一端自由时，μ取2.0；当一端固定另一端铰接时，μ取0.7。

本桥的主墩墩底与承台固结，由于承台下接群桩基础且埋入地面，墩底端可视为固定。主墩墩顶与箱梁固结，当梁的线刚度（变截面梁可取跨中最小截面）与墩线刚度之比大于3时，可认为梁刚度无穷大，墩顶可视为固定端，此时，顺桥向主墩墩身计算长度系数μ可取0.5。本桥顺桥向主梁线刚度与墩身线刚度之比=（3.6×104×28.41/150）/（3.45×104×13.62/110）=1.6＜3.0，墩顶约束处于欠固结状态，即为固结与微移动铰接之间的状态，顺桥向的墩身计算长度系数取值范围为0.5～0.85（0.85＞0.7）。

横桥向主墩墩底约束固结，墩顶约束处于自由与铰接之间的状态，横桥向墩身计算长度系数按0.85～2.0范围取值。

6.2.2 规范法

对于一端固定、一端有转动和水平弹性约束的构件，计算长度系数μ为：

式中：kθ、Kθ、kF、KF分别表示构件转动和水平弹性约束端的相对转动约束刚度系数、转动约束刚度、相对水平约束刚度系数、水平约束刚度；L为构件支点间长度；EI为构件截面抗弯刚度。

2016年河北省城镇居民的可支配收入为28 249元，2017年为30 548元；农村居民人均可支配收入2016年为11 919元，2017年为12 881元。2016年城镇居民人均消费支出19 106元，2017年为20 600元；2016年农村居民人均消费支出9 798元,2017年为10 536元。由统计数字可以看到，城乡居民年收入虽然增长较快，但是农村居民收入增长幅度小于城镇居民，且不同地域农村居民收入差距较大[2]。截至2017年底，河北省依然有39个国家级贫困县，195.67万人享受居民最低生活保障，其中，农村居民160.2万人，占81.87%，反映出城乡收入差距较大的现实问题。

通过查询计算模型中的转动角度和水平位移及其各自对应的内力，便可求出Kθ和KF，根据墩高和墩身截面刚度即可求出式（5）的kθ和式（6）的kF。将这些数值代入式（4），即可求出墩身计算长度系数。

以本桥3号墩为例，求得顺桥向墩身计算长度系数为0.61，计算时的基本参数见表2。

表2 基本参数表

6.2.3 基于欧拉公式的屈曲分析法

压杆的欧拉临界力Fcr计算式为：

显然，已知构件的临界压力Fcr，由式（7）可求出计算长度系数μ为：

利用有限元程序对本桥进行三向屈曲模态分析。结果显示，第1模态为顺桥向屈曲，特征值系数为21；第2模态为横桥向屈曲，特征值系数为24.8。进而求出顺桥向墩身临界压力值为2607801kN；横桥向墩身临界压力值为3079689kN。分别代入式（8），求得顺桥向墩身计算长度系数μ=0.82；横桥向墩身计算长度系数μ=1.54。

由上可知，经验法能够快速有效地确定墩身计算长度系数的取值范围，规范法和屈曲分析法能够进一步量化取值。综合对比3种方法的计算结果，本桥顺桥向墩身计算长度系数取0.75，横桥向计算长度系数取1.5。

6.3 墩身截面尺寸

本文按照顺、横向等稳定的原则来设计墩身截面尺寸，使得桥墩在顺桥向和横桥向的长细比大约相等，从而达到顺桥向和横桥向具有相同稳定承载力的目的，充分发挥构件的材料性能。

刚构桥的主墩墩身顺向计算长度小于横向值，墩身截面设计时，截面顺向尺寸应小于横向尺寸，从而使得顺向回转半径小于横向值，达到相同长细比的目的。同时，这也有利于抵抗较大的横向风荷载。

为减小上部主梁的负弯矩且增大桥墩顺桥向的抗弯刚度，本桥采用双肢矩形墩。为加强双肢墩之间的联系和提高墩身稳定性，沿墩高每隔一定距离设置1道墩间系梁，形成格构式墩柱。

双肢墩身截面示意图见图8。

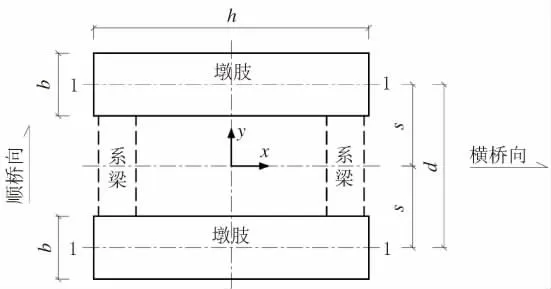
图8 双肢墩身截面示意图

6.3.1 横桥向墩身长细比

绕y轴，双肢墩的横桥向回转半径ry计算式为：

式中：Iy为双肢截面绕y轴的惯性矩；b为单肢墩身截面顺向尺寸；h为墩身截面横向尺寸；A为双肢总截面面积；A1为单肢截面面积；ry1为单肢截面绕y轴的回转半径。

整体双肢墩的横桥向长细比计算式为：

式中：λy为横桥向墩身长细比；L0y为横桥向墩身计算长度。

可见，整体双肢墩的横向回转半径等于单肢墩的横向回转半径；整体双肢墩的横向长细比等于单肢墩的横向长细比。墩身横向长细比计算时，只需通过调节单肢墩的截面尺寸即可完成。

本桥取3号墩为研究对象，墩高120m；墩身截面横向尺寸h值取箱梁底宽度，由图3可得h=11m；单肢墩身截面顺向尺寸b取2.5m。由式（9）得ry=ry1=3.175m；由6.2节结论得横桥向墩身计算长度L0y=1.5×120=180m；由式（10）得横桥向墩身长细比λy=56.7。

6.3.2 顺桥向墩身长细比

绕x轴，整体双肢墩的顺桥向回转半径rx计算式为：

式中：Ix为双肢截面绕x轴的惯性矩；I1为单肢截面绕自身对称轴1-1的惯性矩；s为单肢截面形心距x轴的距离；r1为单肢截面绕自身对称轴1-1的回转半径。

整体双肢墩的顺桥向长细比应取换算长细比，结合式（11），换算长细比计算式为：

式中：λox为顺桥向双肢墩的换算长细比；λx为顺桥向双肢墩理论长细比；λ1为顺桥向分肢墩的长细比；L0x为顺桥向整体墩身计算长度；L1为顺桥向分肢墩的计算长度，取相邻2道系梁的竖向间距。

可见，影响整体双肢墩的顺桥向长细比的因素包括：顺桥向墩身计算长度、沿墩高方向的系梁间距、分肢墩身截面绕自身对称轴的回转半径（与截面尺寸有关）、两分肢墩的中心距。

本桥取3号墩为研究对象，墩高120m；墩肢中心距d取6.5m；沿墩高每隔40m设置1道系梁。由6.2节结论得L0y=0.75×120=90m，由式（11）得rx=3.329m，由式（12）得λox=61.7。

由以上参数可得，横桥向墩身长细比λy=56.7。该数值与顺桥向墩身长细比（λox=61.7）比较接近，基本满足等稳原则的设计要求。

6.4 验算要点

验算墩身时，除在平面内按偏压构件验算外，还需在平面外按轴心受压构件验算，此时需要考虑稳定系数，而稳定系数与墩身截面尺寸有关（矩形截面时为短边边长b）。当墩身为变截面柱时，b值可采用墩柱中间段尺寸（墩顶、底截面的平均值）。

7 抗震

关于地震的产生及破坏规律，人类一直处在探索阶段，实际地震的破坏机理及效应与结构理论计算的各种假定及结果总是存在不确定因素。作为抗震计算的各种方法，仅能作为对地震效应的粗略估算，但从震害程度来看，抗震计算结果对工程抗震具有明显效果，不可轻视。

特大桥梁应注重抗震概念设计，优选结构体系和规则性布置，加强构造措施，强化结构的整体抗震性能。

7.1 超越概率与重现期

非规则桥梁的地震参数应结合公路桥规和地震安评报告取值，而地震安评报告往往按照超越概率和重现期来提供地震参数（如反应谱峰值加速度），与公路桥规参数的对应性不直观。因此，掌握其推导公式或原理，可提高桥梁设计师对规范参数的理解和选用，避免出现原则性错误。

超越概率是指在给定的时间段内，工程场地发生不小于指定的地震烈度值或动参数值的概率。重现期是指地震重复发生一次的时间间隔（年数）。

描述地震活动的随机过程可采用泊松分布模型模拟，其计算式为：

式中：λ为发生概率；n为重现期；T为设计年限；P为超越概率。

本桥按A类抗震设防类别设计，地震安评报告按照设计年限和超越概率共提供6类反应谱参数，分别为3个50a超越概率值（2.5%、10%、63%）和3个100a超越概率值（2%、10%、63%）。根据式（15）计算以上6类情况，对应的地震重现期分别为1975a、475a、50a和4950a、949a、101a。

最终，E1水准选用50a超越概率值为10%的地震参数（对应重现期475a）；E2水准选用50a超越概率值为2.5%的地震参数（对应重现期约2000a）。

7.2 减重

地震作用效应的本质是质量产生的惯性力。因此，优化结构构件的尺寸和材料，减轻桥梁结构的自身重量，可有效减小地震作用效应力。本桥箱梁采用C60型混凝土，墩身采用C50型混凝土。

上部结构若采用斜腹梁截面可减少约2000m3混凝土，但综合考虑施工作业困难，最终采用直腹梁方案；箱梁梁高变化曲线采用2次抛物线，相对于1.8次抛物线，一方面能减小底板钢束的径向张力，另一方面也能减小混凝土体积，减小梁体自重；桥墩采用空心薄壁墩，可大量减小墩身自重，有利于抗震计算。

7.3 刚度

对于连续刚构桥而言，桥墩是其主要的抗侧力构件。本桥墩高80~120m，若墩身采用相同截面，则水平地震力与墩高成非线性反比关系，刚度大的矮墩承受较大水平地震力，刚度小的高墩承受较小水平地震力；同时，高墩将会有较大的墩顶位移，使上部结构产生偏转并导致墩柱承受扭矩，从而严重影响结构的整体抗震能力。

为减小由墩高差异引起的墩身侧向刚度影响，可采取2种处理方式：（1）在矮墩墩顶设置减隔震支座代替墩梁固结，以减小矮墩承受的水平地震力；（2）加大高墩的墩身截面尺寸，增大其刚度，使得各墩刚度接近，均匀分摊水平地震力。

7.3.1 减隔震支座

采用减隔震支座应考虑支座后期养护及更换问题，虽然一些支座的使用寿命在理论上接近桥梁设计使用年限，但本桥所处地理环境难以保证其全寿命，而高空作业又使支座更换难度大。因此，减隔震支座不作为本桥佳选方案。

7.3.2 增大墩底截面

出于美观、造价和施工模板方面考虑，本桥高墩和矮墩的墩顶采用相同断面。墩身截面尺寸由上向下逐渐变大，各墩身竖向斜率一致，在矮墩（墩高80m）墩底的高程水平面内，各墩身截面尺寸相同。因此，若在矮墩底水平面以下范围内将高墩（高度大于80m的墩）墩身刚度做到足够大，便能均衡各墩的侧向抗推刚度。

方法一：将高墩墩底部分的双肢墩合并为整体式墩身，采用相同配筋。经计算，E1地震作用下，各主墩墩身强度验算安全系数相差不大，比值为0.8~1.0，材料强度得到充分利用。

方法二：保持双肢墩不变，矮墩底水平面以下范围的墩身按既有斜率延伸至承台（即墩高越高，墩底截面越大），采用相同配筋。经计算，E1地震作用下，各主墩墩身强度验算安全系数相差明显，比值为0.6~1.0，材料强度未得到充分利用。

方法一的计算效果最佳，但整体式墩身耗费材料多且自重大，经济性差。因此，本桥最终方案采用方法二的分离式双肢墩，且在矮墩底水平面上的所有高墩处增设加强系梁，以达到增强高墩刚度的目的。经计算，E1地震作用下，各主墩墩身强度验算安全系数相差基本合理，比值为0.7~1.0，材料强度基本得到充分利用。分离式双肢墩的桥型立面示意图见图9。

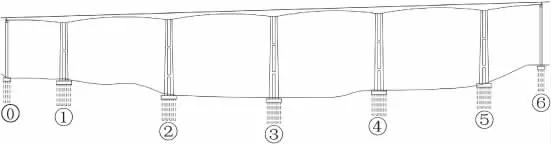
图9 分离式双肢墩桥型立面示意图

7.4 抗震分析方法

7.4.1 反应谱分析法

规范中的地震反应谱通常指加速度反应谱（另外有速度反应谱和位移反应谱），是指在单自由度体系内，地震最大绝对加速度与其自振周期的函数关系。

反应谱法属于线弹性分析方法，其谱值仅采用结构各振型反应的最大值，计算结果偏保守[5]。但由于其计算过程简单直接，桥梁设计初期阶段可采用此方法。由于SRSS法无法考虑振型耦合，计算时，振型组合方式优先选择CQC法。

7.4.2 动力时程分析法

根据每个时间点对应的加速度值，由初始状态逐步积分求解运动方程，求得结构相关计算参数，从而记录结构在整个地震时间过程中的地震反应（速度、位移和加速度），称为动力时程分析。其计算式为：

式中：[M]为结构的质量矩阵；[c]为结构的阻尼矩阵；[k]为结构的刚度矩阵；｛u"｝、｛u'｝、｛u｝分别为加速度、速度和位移向量；｛ug｝为输入的地震波加速度向量。

当结构保持弹性状态时，刚度矩阵不变，称为弹性时程分析；当结构进入弹塑性阶段时，构件的刚度要按照恢复力特征曲线上的位置取值不断变化，此时称为弹塑性时程分析。

相比反应谱法，动力时程分析法更能模拟结构的实际受力状态，对于特殊桥梁的抗震设计，应采用此方法进行精细计算或作为补充计算。

8 高强材料

为了提高主墩墩身承载力、减小墩身截面尺寸和降低构件自重，墩身受力控制截面的主筋可采用高强度钢筋。但选用钢筋牌号时不能盲目，应该有充分的理论依据。

钢筋混凝土受弯、受压构件设计时，应使得钢筋屈服和混凝土压碎（即达到极限压应变）同时发生。

钢筋、混凝土破坏示意图见图10。图中：Nc、ΔL分别为应力、应变。

图10 钢筋、混凝土破坏示意图

对于轴心受压构件，当采用C50强度等级的混凝土时，正截面混凝土极限压应变εcu=ε0=0.002+0.5（fcu，k-50）×10-5=0.002。其中：εcu为正截面混凝土极限压应变；εo为混凝土应力达到混凝土轴心抗压强度设计值时的混凝土压应变；fcu，k为混凝土立方体抗压强度标准值。

由于混凝土和钢筋之间存在胶结力、摩擦力及机械咬合效应，假设此时钢筋的应变同样为0.002，则钢筋应力σ=εcuEs=0.002×206000=412.7MPa（其中Es为钢筋的弹性模量）。可见，对于轴心受压构件（C50混凝土），若采用HRB400钢筋（屈服强度400＜412.7MPa），当混凝土压碎时，钢筋已屈服，钢筋强度得到充分利用；若采用HRB500钢筋（屈服强度500＞412.7MPa），混凝土压碎时，钢筋仍未屈服，钢筋强度未能充分利用。

对于偏心受压构件，混凝土正截面极限压应变εcu=0.0033-（fcu，k-50）×10-5=0.0033，假设此时钢筋的应变也为0.0033，则钢筋应力σ=εcuEs=0.0033×206000=679.8MPa。可见，对于C50混凝土的偏心受压构件，若采用HRB500钢筋（屈服强度500＜679.8MPa），当混凝土压碎时，钢筋已屈服，钢筋强度能得到充分利用。

公路桥规的裂缝宽度Wcr计算式为：

式中：C1、C2、C3分别为钢筋表面形状系数、长期效应影响系数、构件受力相关系数；σss为钢筋应力；c为最外排纵向受拉钢筋的混凝土保护层厚度；ρte为纵向受拉钢筋的有效配筋率[4]；d为钢筋直径。

由于高强钢筋能承受较大的钢筋应力，当式（17）中的钢筋直径d不变时，钢筋应力值σss的增加会加大裂缝宽度值Wcr。因此，采用高强钢筋时，应关注构件的裂缝宽度。

本桥墩身采用C50混凝土，属于偏心受压构件，在墩身顶、底截面一定范围内，墩身纵向受力主筋采用HRB500牌号的高强度钢筋，其余位置采用HRB400钢筋，可满足设计及计算要求。

9 其他

（1）体外预应力。为减小桥梁后期挠度，可预留体外预应力束的转向块设计，以备后期养护增设体外预应力筋。

（2）边跨预应力。由于弯折角度会影响预应力损失，箱梁边跨预应力束沿竖向多排布置时，弯折角度大则匹配短束，弯折角度小则匹配长束。

（3）节点。双肢空心墩的墩梁连接节点处，应考虑墩身主筋的延伸锚固空间。主墩与箱梁连接处，箱梁横隔板中心线与墩中心线宜重合，可沿墩壁中心线设置多道箱梁横隔板。当双肢空心薄壁墩之间设置空心截面系梁时，应考虑系梁主筋的延伸锚固长度及其与墩身主筋的空间冲突。系梁腹板厚可小于墩身壁厚，系梁腹板中心线与墩身壁厚中心线重合，使得系梁主筋延伸于墩身主筋中间位置，避免各自主筋的空间冲突。

（4）铺装。采用悬臂浇筑法施工的箱梁，梁段连接处的连续平整性难以保证。成桥时，施工单位通过在桥面不连续处加铺混凝土层来保证平整度，增加了桥面荷载负担。因此，在桥梁设计阶段应预先考虑一定厚度（一般不小于6cm）的混凝土调平层荷载，增大计算安全储备。

10 结语

一座桥梁的设计过程，不是对同类桥梁的简单复制和模仿，应在满足业主需求的前提下，最大化实现桥梁本身的综合价值。桥梁设计中，应重视概念设计的作用和意义。