基于传热学机理对回流焊炉温度场优化控制问题的研究

童孝雯 汪春龙 燕少朋

摘要：针对回流焊炉温度场优化控制问题，该研究通过传热学机理分析，运用导热微分方程、牛顿冷却定理建立了炉温曲线模型，并以高温回焊炉的制程界限为约束，基于遍历搜索算法针对炉温曲线进行了多目标优化，得出了炉温优化曲线对应的炉温设置参数和传送带速度参数。结果表明：小温区1～5、6、7、8～9的设置温度分别为185℃、205℃、232℃、265℃，传送带运动速度为72cm/min，并可绘制出满足条件的最优炉温曲线。本文的分析思路与求解方法能够为回流焊炉的实际工程应用提供最优炉温曲线的方案设计。

关键词：炉温曲线;导热微分方程;牛顿冷却;遍历搜索;优化模型

中图分类号：TB文献标识码：Adoi：10.19311/j.cnki.1672-3198.2022.01.064

0引言

回流焊炉系统的温度场状态控制，一直是研究的热点。其可在不同的目的和角度下建立温度控制系统模型，从而研究工业炉的生产过程，对实际工程应用有较大的指导意义。

从热交换机理出发建立工业炉温度场，到基于多元统计投影原理的偏最小二乘法来研究冶金加热炉的温度分布状态;再到Patisson F等人在工业炉传热过程基础上综合考虑炉内物理、化学反应，建立了一维温度分布。为了完善工业炉热工理论，需借鉴计算流体力学和数值分析传热学等方法，实时采样，结合计算机技术实时分析方法。对于现阶段电子工业的发展，可进一步对回焊炉中炉温进行分析研究。对于现今电子电路的发展，可分析回焊炉中各种机制之间的机理关系，如炉温曲线优化，还可以从金属含量不同的焊膏，PCB板的材质、厚度，加热的温度分布区间和传送带的变化速率等角度去考虑问题;再者，如Lee分析了炉温与焊点失效模式的关系，如赵俊伟等从钎焊机理入手，由金相分析指出在流区峰值温度一般应该在220℃左右，峰值温度低于200会形成不良焊接。

本研究主要针对回流焊炉温度场优化控制问题，基于传热学机理，建立了回流焊炉的温度场分布模型，并针对制程界限的约束条件和最优炉温曲线进行了优化，为实际工程应用提供了解决方案和优化算法。

1数据来源与假设

1.1数据来源

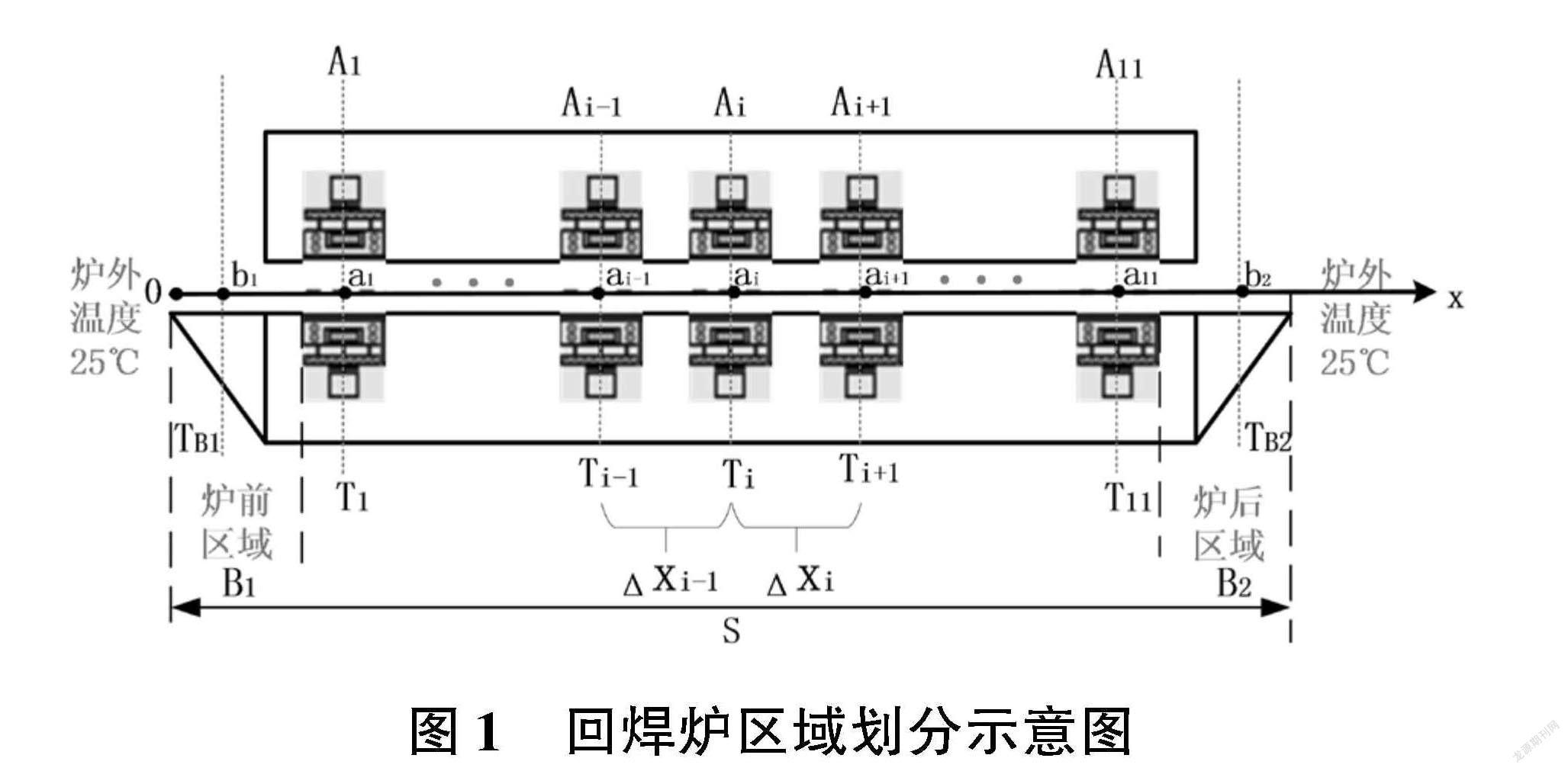
该研究数据来源于2020年全国大学生数学建模大赛A题。标记第i个小温区为Ai（k=1，2，…，11），A1～A5小温区的温度为T15，A6小温区的温度为T6，A7小温区的温度为T7，A8～A9小温区的温度为T89，A10～A11小温区的温度为T1011，炉前区域为B1，炉后区域为B2，其中虚线位置表示每区域的中心位置，具体标记示意图如图1所示。

1.2假设说明

为了便于解决问题，提出以下假设：（1）假设电路板的焊接区域在各方向上热通量相同;（2）假设炉内热空气向电路板传导的热量全部用于焊接区域上的升温;（3）忽略因传送带运动使炉内空气流动对温度场分布所产生的影响。

2基于传热学机理的炉温曲线模型建立与求解

2.1炉温曲线模型的建立

焊炉内温度场分布：

θs（x）=1-xLθ1+xLθ2θs（0）=θ1d2θsu2=0θs（L）=θ2（1）

其中，L为两小温区之间的温度;θ为各温区边界的温度值。故一维稳态热传导的温度場是呈线性分布的。

假设各小温区的中心温度稳定于对应加热炉的温度，炉前、炉后中心温度为室温。故均匀的一维热传导温度场，在不同温区的中心线间的温度场是线性分布的。针对一般情况：相邻温区间，即ai≤x≤

ai+1，若Ti+1=Ti，则该区间内温度呈现均等分布;若Ti+1≠Ti，则温度呈现线性变化分布，对各温区定量计算可得：

Tf（x）=T1-25a1-b1+25  ，  b1≤x<a1Ti+1-Tiai+1-ai+Ti  ，  ai≤x<ai+1，i=1，2，…，1025-T11b2-a11+T11  ，  a11SymbolcB@x<b2（2）

可通过热传导微分方程求解炉前炉后区域的温度场分布：

Tt=D2Tx2T（x，0）=25oCT（0，t）=Ti，（i=15，89）T（x-0，t）=T（x+0，t）（3）

运用热传导方程有限差分法、追赶法可求解出炉前炉后区域的温度场分布。

因为炉内热空气与电路板上焊接区域的热交换以热对流方式进行，所以电路板上焊接区域内的温度变化可用牛顿冷却公式求解：

Q=αF（Tf-Tw）（4）

α=ku（5）

其中，α为热交换系数，Tf为炉内流体热空气温度，Tw为电路板焊接区域处温度，u为流体温度的相对速度。

焊接区域吸收热量为：

Q=cmΔTw（6）

ΔTw=Tw（k+1）-Tw（k）（7）

假设炉内热空气向电路板传导的热量全部用于焊接区域上的升温，忽略热交换过程中热量的损失：

dQchdx=αF（Tf（x）-Tw（x））dQindx=cmΔTw（x）ΔTw（x）=Tw（x+Δx）-TwxdQchdx=dQindx（8）

Tw（x+Δx）=Twx+αFcm（Tfx-Twx）（9）

其中，Qin为进入温度场的热量，Qch为电路板从环境中吸收的热量，c，m分别是电路板的热容和质量，ΔTw为电路板焊接区域处的温度差，Tf1为炉内的初始温度。

构建有限元函数关系式的求解：初始状态下Tw0与室内温度相同，即Tw0为25℃：

Q=αF（Tf0-Tw0）=cm（Tw1-Tw0）（10）

由上式可得电路板上焊接区域处的温度随位移的变化关系式：

Tw1=Tw0+αFcm（Tf0-Tw0）（11）

可解得电路板上焊接区域处温度以位移为参数的通式：

Tw（k+1）=Twk+αFcm（Tfk-Twk）k=0，1，2…n（12）

L=SNk（13）

平均对流换热系数α的研究：在本文中对流换热系数主要研究的是对流换热的强弱，其影响因素有：热风速度v，基板长度L，气体粘度μ，气体运动粘度系数λ，普朗特数Pr。α的函数关系式如下所示：

α=f（v，L，μ，λ，Pγ）f（v，L，μ，λ，P）=0.664v12Pγ13λ/μL12β=Pγ13λ/μL12（14）

求解得β的相关函数值。综上所述，可得：

Tw（k+1）=Twk+0.664v12βFcm（Tfk-Twk） k=0，1，2，…nTw（x+Δx）=Twx+0.664v12βFcm（Tfk-Twk）

（15）

通过上述关系式通过有限差分法可得出炉温曲线。

2.2炉温曲线优化模型的建立

优化目标：在上述的研究基础上，满足制程界限的条件，使炉温曲线超过217℃到峰值温度所覆盖的面积最小，同时还需保证以峰值温度为中心线的两侧超过217℃的炉温曲线尽量对称。

2.2.1曲线对称系数模型的建立

在满足温度曲线超过217℃到峰值温度所覆盖的面积最小目标基础上，要求以峰值温度为中心线的两侧超过217℃的炉温曲线尽量对称。对于炉温曲线对称要求，以峰值为中心线为y轴，峰值区域时间为x轴建立坐标，如图2所示。

对超出217℃到峰值的整体温度曲线区域取对称时间点作温度切线，如上图右侧图片所示，Li表示为作切割划分的各点切线，ni、n'i表示对称轴两侧等值划分的各对称点。对于上述，任意i（i∈[1，n]）直线斜率为k1，k2，…，ki。

求解关于对称轴对应的各切线的斜率ki、k'i，使其满足：

ki+ki'=0（16）

记γ为满足对称的曲线对称系数，满足下述公式：

γ=∑ni=1ki+ki'（17）

当两边对称度越高时，在误差允许的范围内，γ值约趋于0。

2.2.2优化判别系数

设定δ为求解阴影面积最小和满足对称条件的优化判别系数，使其满足：

δ=mA+ny，其中m，n为各自权重，设定其为：

δ=mA+nym=n=1orδ=mA+nγm=n=1（18）

2.2.3优化搜索模型

通过遍历搜索算法，以制程界限条件为主要约束，通过Matlab编程遍历搜索算法进行多目标优化求解，求解思路如下：

步骤一：进行遍历搜索过程中速度区间和各个温度区间的划分。

步骤二：明确遍历搜索过程中制程界限的约束条件。

步骤三：进行曲线对称系數、优化判别系数的求解。

步骤四：进行曲线对称系数、优化判别系数的判别与挑选。

3模型的结果与讨论

3.1模型的结果

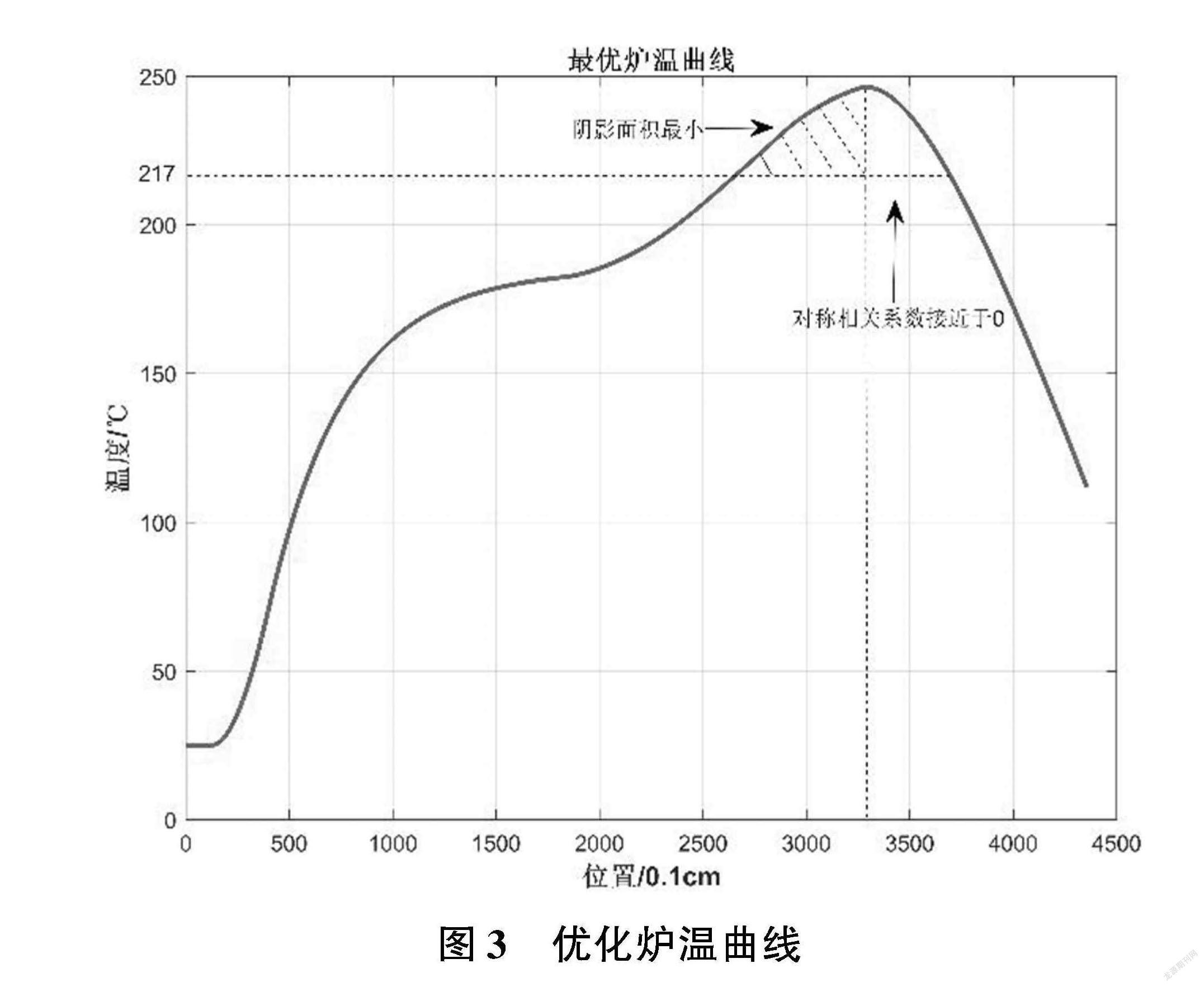
考虑算法的运行速度，遍历优化算法编程中可取速度的步长为5cm/min，温度步长均为5℃进行优化搜寻，得到在制程界限约束条件下的若干条炉温曲线，选取满足其中超过217℃到峰值温度所覆盖的面积最小并且以峰值温度为中心线的两侧超过217℃的炉温曲线应尽量对称这些要求的炉温曲线如图3所示。

通过这条优化的炉温曲线即可求得对应各个温区的温度，传送带的运动速度和相应的指标值分别为：T15=185℃，T6=205℃，T7=232℃，T89=265℃，v=72cm/min，δ=1086.4。

3.2模型的检验与分析

3.2.1可视化定性验证

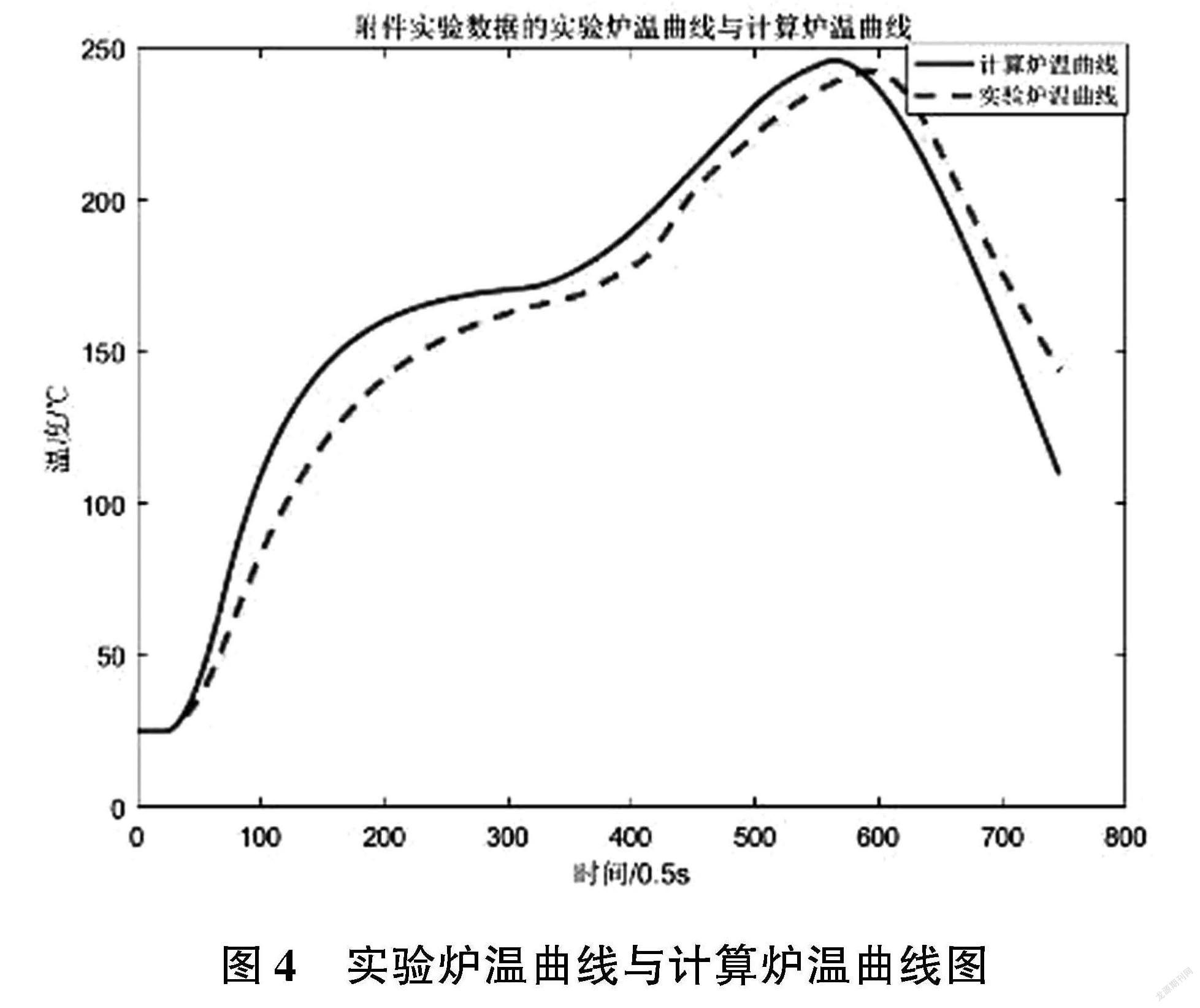
炉温曲线模型的检验，主要针对附件中的实验数据，运用建立的炉温曲线机理模型，对已知的各小温区数据、传送带运动速度数据进行求解，得出计算炉温曲线。最后，对实验炉温曲线与计算炉温曲线可视化处理，直观地通过曲线图像比较、分析实验炉温曲线与计算炉温曲线，进而检验模型的合理性。

由实验炉温曲线与计算炉温曲线的变化趋势、分布状况，可得在一定程度上实验炉温曲线与计算炉温曲线具有较高的相似性，即可说明在一定程度上所建立的炉温曲线具有较高的合理性。

3.2.2判别因子定量验证

不妨将制程界限作为判别因子，将实验炉温曲线视为客观上的准确值，进而针对制程界限判别因子进行定量计算，并对比选定的准确值进行相对误差计算，进而讨论模型的合理性与准确性。通过编程求解可得具体相对误差如表所示。

由上表可得，温度上升斜率与温度下降斜率的相对误差相对较大，可能是因为温度的变化速率对焊炉内温度场分布较为敏感造成的。相对而言，温度上升过程中在150℃～190℃的时间、温度大于217℃的时间、峰值温度得相对误差相对较小，故可以认为该机理模型求解的值具有一定的准确性与可靠性。

3.2.3模型的误差分析

为了便于模型的建立，本文忽略了传送带运动、热量密度集中、热辐射等因素对焊炉内温度分布的影响。事实上，焊炉内温度场的分布将受到以上所列因素的影响，故产生了必然的误差。同时，温度的变化速率受温度场分布的影响是敏感的，故可认为表2中的较大误差是由此产生的。

4结论

通过建立回流焊炉温曲线模型，针对回流焊炉的工作目标，运用炉温曲线优化模型，基于遍历算法进行炉温曲线优化参数的求解，以能够为实际工程应用提供可参考的参数方案。对于实际工程项目产生的相关问题，可以从机理分析出发，应用本文中的思路与求解方法，通过现场测试的实验数据，对理论值进行一定的修正后，能够找到符合实际情况的各工作参数的方案，在参数方案下对机器进行控制，可以更加有效地实现想要达到炉温优化曲线的结果，以指导实践。

参考文献

[1]Fabrice， Patisson， Etienne，等. Coal pyrolysis in a rotary kiln： Part I. Model of the pyrolysis of a single grain[J]. Metallurgical & Materials Transactions B， 2000.

[2]王宁.回流焊温度控制系统的建模与实现[D].咸都：西南交通大学，2011.

[3]Lee N C. Optimizing the reflow profile via defect mechanism analysis[J]. Soldering Surface Mount Technology，1999.

[4]赵俊伟，聂延平，赵志平，等.再流区工艺参数对焊接可靠性的影响[J].电子工艺技术，2001，（2）：60-63.

[5]龚雨兵.再流焊炉温曲线优化研究[J].热加工工艺，2013，42（015）：187-190.

[6]史策.热传导方程有限差分法的MATLAB实现[J].咸阳师范学院学报，2009，24（4）：27-29，36. DOI：10.3969/j.issn.1672-2914.2009.04.009.

[7]张兴中，黄文，刘庆国，等.传热学[M].北京：国防工业出版社，2011.