一种具有多对称同质吸引子的四维混沌系统的超级多稳定性研究
2022-02-24黄丽莲姚文举项建弘王霖郁
黄丽莲 姚文举 项建弘 王霖郁
(哈尔滨工程大学信息与通信工程学院 哈尔滨 150001)
(哈尔滨工程大学先进船舶通信与信息技术重点实验室 哈尔滨 150001)
1 引 言
混沌是非线性动力学系统所具有的一类复杂动力学行为,它表现出确定性非线性系统的内在随机性[1]。混沌由于其初始值敏感性和伪随机性[2],已广泛用于电子工程[3]、信息工程[4]、加密算法[5,6]、安全通信[7,8]和其他领域[9—11]。1963年,美国气象学家洛伦兹[12]提出了第1个混沌系统模型,它引起了科学界的广泛关注,之后又不断有新的混沌系统被发现。1986年,蔡少棠提出了著名的蔡氏电路[13,14],首次实现了混沌与电路之间的结合,是最简单的混沌振荡电路之一。2002年Lü等人[15]提出了一种将Lorenz和Chen的系统连接起来的过渡混沌系统。
2008年,惠普实验室第1次制备出忆阻器[16],这引起了忆阻器研究和应用的热潮。由于忆阻器的非线性,它被用于构造新型的混沌系统。2008 年,Itoh 和 Chua[17]共同提出了基于忆阻器的蔡氏混沌电路,其动力学分析结果表明替换之后的电路的动力学行为与典型的蔡氏电路相比更加复杂。2010年,Bao等人[18]采用光滑磁控忆阻和一个负电导的组合替换蔡氏二极管,提出了基于忆阻的蔡氏混沌电路,重点研究了电路参数和初始条件对忆阻混沌电路动力学特性的影响。2016年,闵富红等人[19]提出一种基于双曲正弦函数的新型磁控忆阻器模型,将其用于构造新型忆阻混沌系统,并利用新系统混沌序列对图像进行加密。
最近几年,多稳定性[20—25]与超级多稳定性[26—33]成为人们的研究热点。多稳定性是许多非线性系统中一种常见的现象,它是指在相同的系统参数设置下,多种吸引子共存的现象。当在相同的系统参数设置下,无限多吸引子共存的现象就称为超级多稳定性。2019年,Wu等人[23]通过将两个正弦非线性引入简单的3维线性动力系统中,提出了一种新颖而简单的3维混沌系统。新系统具有9个平衡点,可以产生多种不同类型的共存吸引子,也称为多稳定性。2020年,文献[24]提出一个没有线性项的3维混沌系统,并对该系统进行了动力学分析,发现该系统可以产生周期轨、混沌振荡、周期窗和共存吸引子等现象。2019年,Ahmadi等人[31]提出了一种具有超级多稳定性的5维混沌系统。该系统具有曲线型的线平衡点,可以产生无限多共存吸引子。2020年,Gong等人[32]在Sprott C系统中引入线性状态反馈控制器,提出了一种具有无限多个平衡点的4维混沌系统。尽管新的4D混沌系统只有两个非线性项,但是它具有丰富的动力学特性,例如隐藏吸引子和共存吸引子。同年,文献[33]将忆阻器引入一个3维混沌系统中,设计了一个具有离散分岔图的4维忆阻混沌系统。该系统不仅具有异质多稳定性,也具有同质多稳定性,同时还具有超级多稳定性。一般使用忆阻器设计的混沌系统都会具有线平衡点,但是本文没有使用忆阻器也使得设计的混沌系统同样具有线平衡点,达到了和使用忆阻器进行设计一样的效果。
异质多稳定性是指混沌系统产生不同形状的吸引子,而同质多稳定性是指系统可以产生幅度、频率或空间位置不同,但形状相同的吸引子。现有的研究混沌系统多稳定性的文献几乎都是讨论混沌系统的异质多稳定性,而同质多稳定性却鲜有报道。在此基础上,本文提出一种具有无限多对称的同质吸引子的4维混沌系统。该系统具有很大的初值变化范围和除零点外恒定的Lyapunov指数谱,不同于文献[33],该系统还具有中心对称的离散分岔图。
本文的其余部分安排如下。在第2节,介绍新系统的无量纲方程,并对系统进行基本的动力学分析,包括对称性、耗散性、平衡点和稳定性。在第3节,利用相轨图、Lyapunov指数和庞加莱截面分析了该系统混沌吸引子的动力学行为。在第4节,通过分岔图和Lyapunov指数谱研究了混沌系统的超级多稳定性,分析结果表明该系统具有无限多对称的同质吸引子和中心对称的离散分岔图。在第5节,对新系统进行电路仿真实现并给出仿真结果,其验证了数值仿真的正确性。最后,对本文进行了总结。
2 4维混沌系统模型
2003 年,Liu等人[34]提出了一个具有5个平衡点的3维混沌系统,可以产生一个4翼混沌吸引子。然而,在 2004 年,Liu 等人[35]证明了它产生的仅仅是两个共存的位置排列十分紧密的2翼吸引子,即上述 Liu系统是个伪4翼混沌系统。它属于广义Lorenz 系统,其无量纲方程如式(1)所示。

2.1 对称性
对称性广泛存在于具有偶数个吸引子的混沌系统中。如果进行变换(x,y,z,w)↔(-x,-y,z,-w),忆阻混沌系统式(2)是不变的,这表明系统式(2)在状态空间中关于z轴对称。
2.2 平衡点和稳定性

2.3 耗散性
3 混沌系统的动力学行为分析
3.1 相轨图和Lyapunov指数
在这一节通过Lyapunov指数和相轨图的方法对系统式(2)进行进一步的研究。当参数a=4.8,b=5,c=21.3,d=5,e=0.01,f=0.1时,系统式(2)可以产生如图1所示的混沌吸引子。

图1 混沌吸引子的相轨图
Lyapunov指数描述了被扰动的初始条件的指数发散率,是判断混沌的有效工具。本文采用龙格库塔(RK45)方法求解ODEs,同时,Lyapunov指数的计算采用著名的 wolf 算法。绝对误差和相对误差都设置为10-4,初始条件为(1,1,0,0)。在以上设置条件下,系统式(2)的Lyapunov指数分别为0.6790, 0.0063, —0.0327和—22.1846。其中最大的Lyapunov指数大于零,此时的系统式(2)是混沌的。
同时,计算系统式(2)的维数如式(7)所示。

3.2 庞加莱截面
庞加莱截面是在系统相空间中截取一个截面。通过仔细观察截面上截点的分布状况,可以判断系统所处的状态。分别取截面z=8和w=1.5,可以得到系统的庞加莱截面如图2所示。在这些图片中可以观察到成片的点,这表明系统具有混沌行为。
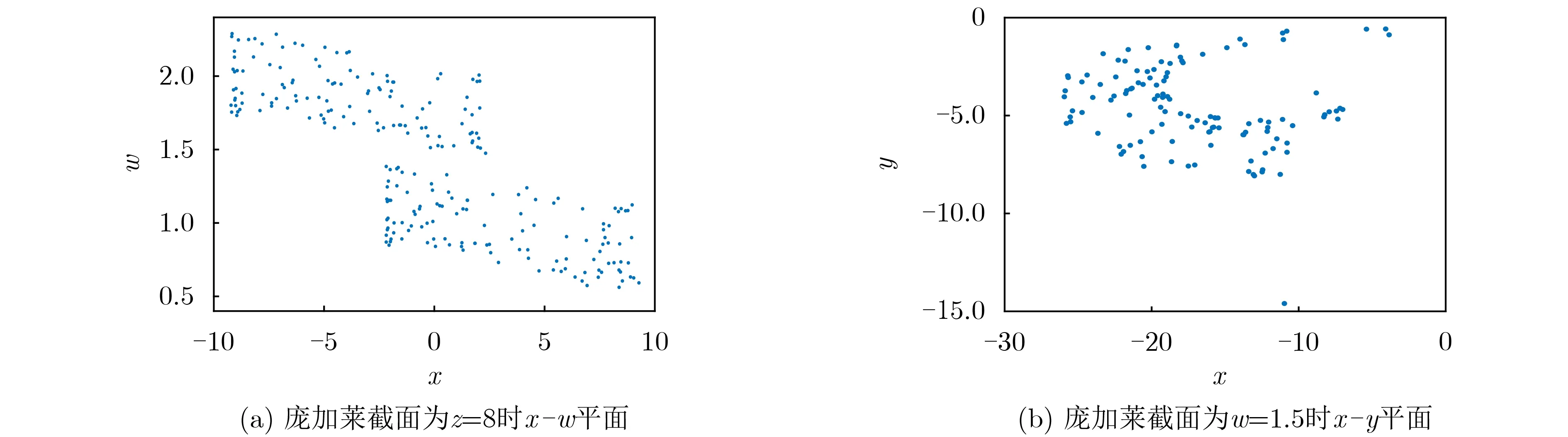
图2 混沌吸引子的庞加莱截面
4 混沌系统的超级多稳定性分析
4.1 异质多稳定性的动力学分析
混沌系统的多稳定性是指,当系统参数固定,取不同的初值时,系统可以产生不同共存吸引子的现象。当产生的共存吸引子的数目趋向于无限多时,这种现象称为超级多稳定性。当系统参数a=4.8,b=5,c=21.3,d=5,e=0.01,f=0.1时,设置初值为(0,0,1,w(0)),给出w(0)在区间[-200,200]内的分岔图和Lyapunov指数谱如图3所示。
图3(a)给出了系统状态变量w随初值w(0)变化的分岔图,可以看出该分岔图由许多离散的小线段组成,且近似呈一条直线排列。在[-35,35]区间之外,状态变量w出现较大范围的变化,表明系统在该区间内产生的混沌吸引子的幅度较大。从图3的相轨图中可以看出,在w(0)位于[-35,35]区间内时,系统产生双涡卷共存吸引子,而w(0)位于该区间之外时,系统产生四涡卷吸引子。图3(a)的分岔图中的状态变量w呈现无限多的稳定的混沌状态,表明该系统可以产生无限多共存吸引子,即该系统具有超级多稳定性。图3(b)给出了系统随初值w(0)变化的Lyapunov指数谱,可以看出,除了w(0)=0外,在区间[-200,200]内的Lyapunov指数谱几乎是恒定的,系统的最大的Lyapunov指数大于零,第2个Lyapunov指数等于零,4个Lyapunov指数之和小于零,所以该系统在该范围处于混沌状态。

图3 初值w(0)在[-200,200]区间内变化的分岔图和Lyapunov指数谱
当系统参数设置为a=4.8,b=5,c=21.3,d=5,e=0.01,f=0.1时,设置初值为(0,0,1,w(0)),w(0)分别取±30,±90时,该系统产生两个双涡卷和两个四涡卷混沌吸引子如图4所示。取30, —30, 90,—90时,分别对应相轨图中蓝、红、粉、青吸引子。通过观察可以发现,这些混沌吸引子是沿着w轴呈现出线性分布的,这与前文系统分岔图的分析结果相一致。通过上述分析可以发现,该系统可以产生结构不同的双涡卷和四涡卷混沌吸引子,因此该系统具有异质多稳定性。
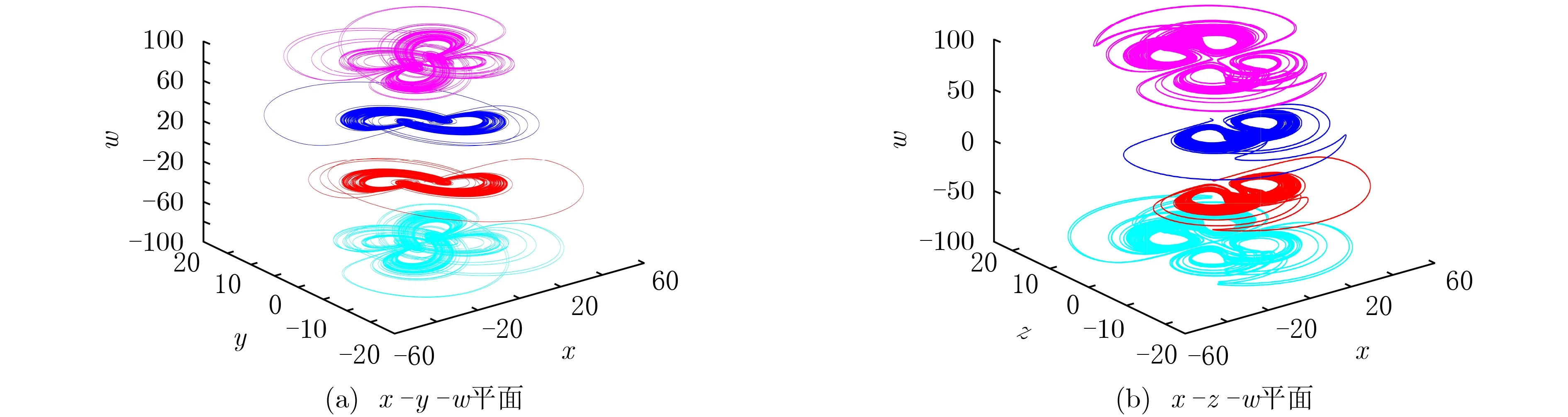
图4 无限多共存吸引子的相图
4.2 同质多稳定性的动力学分析
当系统参数设置为a=4.8,b=5,c=21.3,d=5,e=0.01,f=0.1,初值设置为(x(0),0,1,0)时,给出x(0)在[-103,103]区间内的状态变量w的分岔图和Lyapunov指数谱如图5所示。
从图5(a)可以看出,系统的状态变量w随初值x(0)变化的分岔图不同于一般混沌系统的分岔图,呈现出许多离散的小线段,且集中分布在倾斜的带状区域内。小线段表明系统处于混沌状态,但是其离散的位置分布表明随初值的变化,吸引子的空间位置是不连续的。状态变量w呈现出无限多种稳定的混沌状态,这意味着该系统具有超级多稳定性。通过观察可以发现,该离散分岔图是中心对称的,这可以用吸引子空间位置的对称性来解释。从图5(b)可以看出,该系统在初值x(0)不等于零时,其Lyapunov指数谱保持恒定,且最大Lyapunov指数大于零,表明该系统处于混沌状态。该初值下产生的混沌吸引子的形状与图4所示吸引子类似。可以发现,该系统具有很多形状和大小一样,但是空间位置不同的共存吸引子,因此该系统具有同质多稳定性。
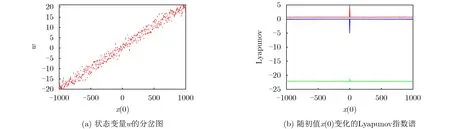
图5 初值x(0)在[-103,103]区间内变化的分岔图和Lyapunov指数谱
基于本系统的特殊性,初值(0,0,1,0)对系统的影响须单独讨论。当系统初值为(0,0,1,0)时,系统的Lyapunov 指数分别为4.8003, —0.0278, —5.0005和—21.3091。包伯成教授在文献[36]中提出,若混沌系统具有混沌吸引子,则必须同时存在以下条件:(1)至少存在一个正的Lyapunov指数;(2)至少存在某一Lyapunov指数等于零;(3)Lyapunov指数谱之和为负。而该系统第1个Lyapunov指数为4.8003, 4个Lyapunov指数之和为负,但是第2个Lyapunov指数为—0.0278,不足够接近零,故此时系统不处于混沌状态。并且通过相轨图观察了此时系统所处的状态,发现系统在该初始条件下确实不处于混沌状态。
接下来讨论一下系统取其他初值的情况。当系统初值设置为(0,y(0),1,0),给出y(0)在[-103,103]区间内变化时的分岔图和Lyapunov指数谱如图6所示。由图6(a)可以看出,系统随初值y(0)在[-103,103]区间内变化时,状态变量w的分岔图也呈现出许多离散的小线段的形式,表明状态变量w具有无限多种稳定的混沌状态,且该离散分岔图也是中心对称的。从图6(b)可以看出,在y(0)不等于零时,该系统的Lyapunov指数谱保持恒定,且最大Lyapunov指数大于零,表明系统在该范围内始终处于混沌状态。通过上述分析可以得到,该系统具有中心对称的离散分岔图以及除零点外恒定的Lyapunov指数谱。
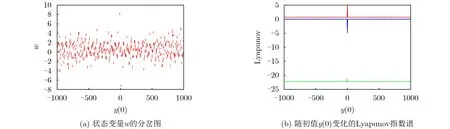
图6 初值y(0)在[-103,103]区间内变化的分岔图和Lyapunov指数谱
初值分别设置为(0,±10,1,0), (0,±60,1,0),(0,±80,1,0)时,系统式(2)可以产生多个同质吸引子,如图7所示。其中,蓝色和红色分别对应初值(0,10,1,0), (0,-10,1,0),粉色和青色分别对应初值(0,60,1,0), (0,-60,1,0),黄色和黑色分别对应初值(0,80,1,0), (0,-80,1,0)。从图中可以看出,这些共存吸引子有两种不同的结构,空间位置有所不同,但是它们都是沿着w轴平行分布。其吸引子沿着w轴平行分布的空间位置正好与图6(a)分岔图中的许多离散的小线段相对应。

图7 无限多同质吸引子的相图
当系统设置初值为(0,1,z(0),0),给出z(0)在[-103,103]区间内的分岔图和Lyapunov指数谱如图8所示。
从图8(a)可以看出,初值设置为(0,1,z(0),0),初值z(0)在[-103,103]区间内变化时,状态变量w的分岔图也呈现出许多离散的小线段的形式,同样表明了该系统具有超级多稳定性。但是该离散分岔图不是中心对称的。图8(b)与图6(b)相似,在z(0)不等于零时,该系统的Lyapunov指数谱保持恒定,且最大Lyapunov指数大于零,表明系统在该范围内始终处于混沌状态。

图8 初值z(0)在[-103,103]区间内变化的分岔图和Lyapunov指数谱
4.3 无限多同质吸引子的对称性
显然,如果进行变换(x,y,z,w)↔(-x,-y,z,-w)系统式(2)是不变的,这意味着(x,y,z,w)和 (-x,-y,z,-w)都是系统方程的解。系统式(2)的这种对称性质可以用来解释状态空间中对称共存吸引子的存在。如果将系统参数设置为a=4.8,b=5,c=21.3,d=5,e=0.01,f=0.1,初值分别设置为(x(0),y(0),z(0),w(0)) 和(-x(0),-y(0),z(0),-w(0)),系统可以产生成对关于z轴对称的共存吸引子。如图9所示,蓝色和红色是一对吸引子,粉色和青色是另一对吸引子,蓝色对应初始条件,红色对应初始条件,粉色对应初始条件,青色对应初始条件。该对称性同样适用于该系统参数下的其他的混沌吸引子。
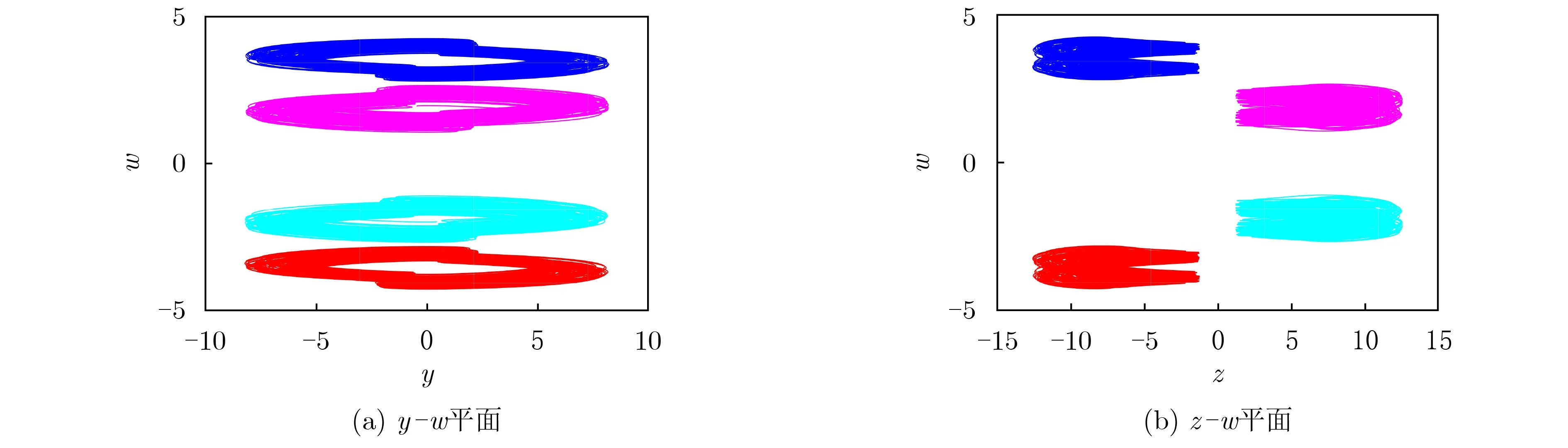
图9 对称的同质吸引子的相图
当系统参数设置如上,系统初值分别设置为(1,1,1,1)和(-1,-1,1,-1)时,分别给出状态变量z和w在时间t=30s内的时域波形图如图10所示。其中蓝色对应初始值(1,1,1,1),红色对应初始值(-1,-1,1,-1)。从时域波形图中可以看出,两个混沌吸引子的状态变量w分别关于x=0,y=0和w=0对称,而状态变量z是完全重合的。由此也可以验证上述结论,即初值分别设置为(x(0),y(0),z(0),w(0))和(-x(0),-y(0),z(0),-w(0))时,系统可以产生成对的关于z轴对称的同质吸引子。
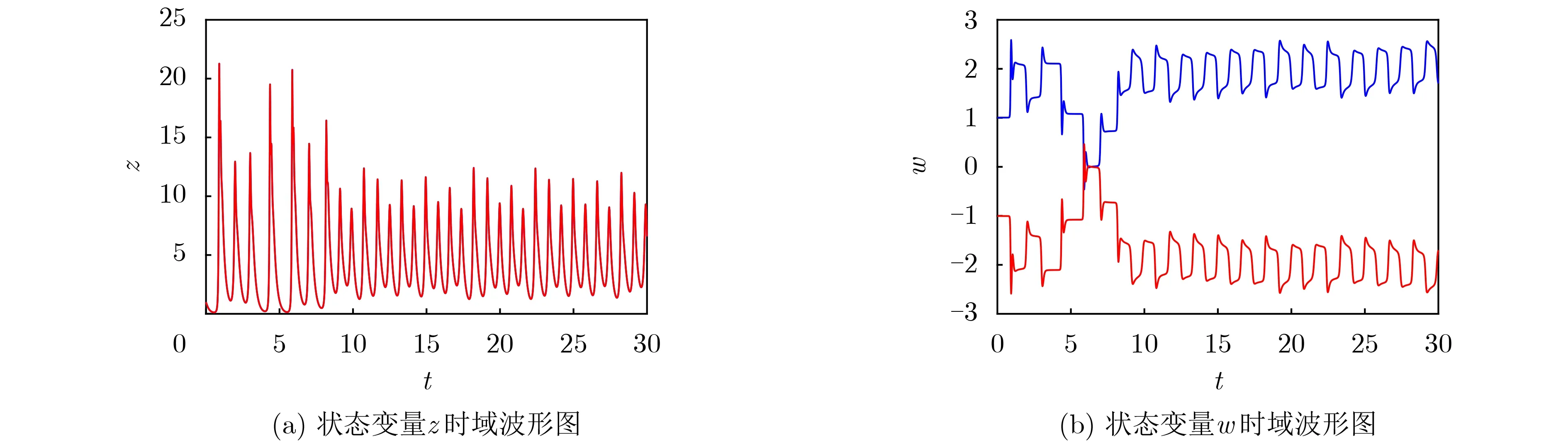
图10 对称吸引子在t=30 s 内的时域波形图
5 电路仿真实现
在本节中,可以通过模拟电路仿真观察所提出的混沌系统的复杂动力学行为。通过使用集成运算放大器、乘法器和其他一些元器件来构建混沌电路,产生混沌吸引子。运算放大器的电源电压为E=±15 V,参考电压是±15 V。所有乘法器的输入和输出范围在—15~15 V。但是,状态变量的值超出了此范围。因此,原系统无量纲方程式(2)必须首先进行尺度变化。所以将状态变量x,y,z和w压缩到原来的1/10,将其限制在运算放大器和乘法器参考电压的范围内。同时考虑时间比例因子 RC,经过尺度变换和时间比例变换后系统式(2)的无量纲方程可以表示为

系统式(2)的模拟电路如图11所示。电路方程式为

图11 系统式(2)的模拟电路图


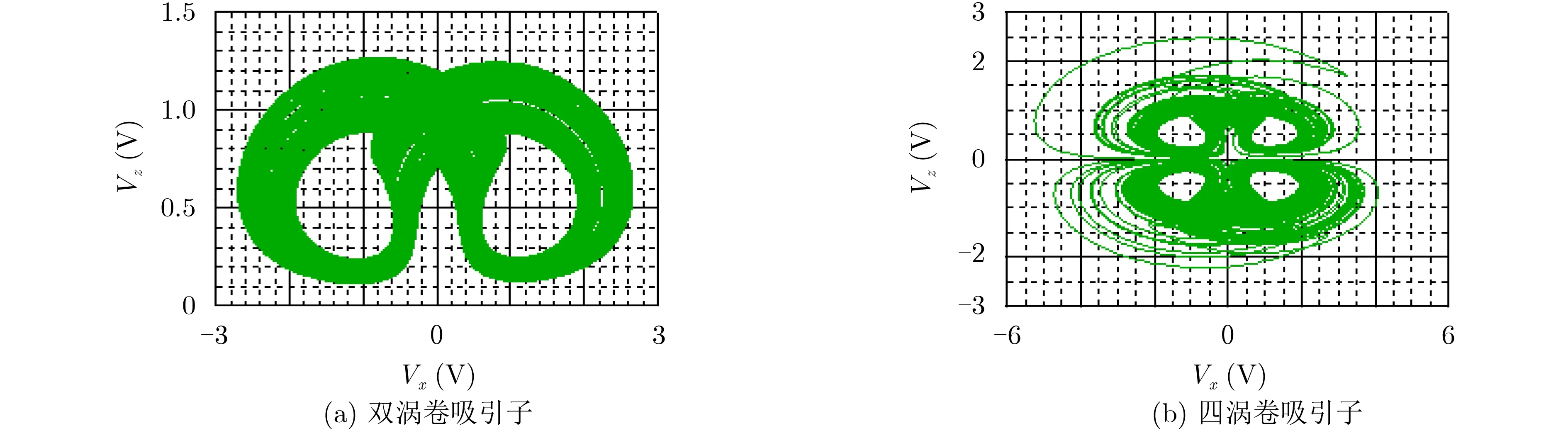
图12 混沌吸引子的Vx—Vz平面电路仿真结果
6 结束语
本文在一个经典3维混沌系统的基础上提出一个新的具有超级多稳定性的4维混沌系统。新系统具有一个线平衡点,可以产生无限多空间位置不同,但大小形状基本相同的同质吸引子。重点利用相轨图、分岔图和Lyapunov指数谱等方法研究了系统初始条件对系统同质吸引子的影响,结果表明该系统具有很大的初值变化范围,除零点外恒定的Lyapunov指数谱以及离散分岔图。不同于现有文献中提及的混沌系统,该系统具有中心对称的离散分岔图,这可以用系统的对称性来解释。进一步地,我们研究了系统初值对称性与吸引子对称性的关系,发现该系统可以产生无限多对称的同质吸引子。最后,利用电路仿真软件搭建模拟电路捕捉该系统的混沌吸引子,其结果验证了数值仿真的正确性。新系统具有复杂的动力学特性,其在基于混沌的信息加密和保密通信领域有着潜在的应用价值。
