面向多路源信号的单通道盲去卷积算法研究

刘 婷 尹甜甜 龚真颖 郭一娜

(太原科技大学电子信息工程学院 太原 030024)

1 引言

单通道盲源分离(Single-Channel Blind Source Separation， SCBSS)是指仅凭借单个传感器就能将所采集到的单路混合信号分离为多路源信号，按照混合方式主要分为线性瞬时混合模型和卷积混合模型[1]。研究最早的用于单通道盲源分离的方法主要是针对线性瞬时混合模型，如设计最优滤波器，但单一滤波器并不能满足实际要求。以总体经验模态分解(Ensemble Empirical Mode Decomposition， EEMD)为基础的非负矩阵分解(Non-negative Matrix Factorization， NMF)[2，3]和独立成分分析(Independent Component correlation Analysis，ICA)[4]等方法，它们假定源信号可以用一组线性组合表示，主要解决线性混合的单通道盲源分离问题，效果较好。但在实际情况下，传播环境很复杂，并且观察到的许多信号是信道衰落和延迟的结果，信号大多数是以卷积的方式进行混合的，这些方法在针对卷积的混合信号分离问题上效果并不理想，不能用来解决更实际的卷积信号的分离问题。

单通道盲去卷积是针对卷积混合模型的单通道盲源分离问题，因其更适用于从一路卷积混合信号中分离和解卷积出源信号，在生物医药工程[5]、语音信号处理[6]、图像复原[7]、地震勘测及自动控制等[8]领域中都有广泛的应用。但由于缺乏混合信息，源信号和混合矩阵都是未知的，因此，这是一个极具挑战但又不得不面对的问题。

较早的盲去卷积算法主要有：Sato[9]和 Godard[10]算法，用来解决源信号的恢复问题。Yellin等人[11]提出基于高阶谱的盲去卷积算法，但需要计算高阶谱，运算量太大，效果欠佳。近年来，神经网络变得越来越流行，许多研究者应用卷积神经网络(Convolutional Neural Networks， CNN)[12]和全连接神经网络[13]来解决源信号的分离和去卷积问题，使用递归神经网络(Recurrent Neural Networks，RNN)[14]从混合的杂音中产生清晰的声音，利用自动编码器(Auto-Encoders， AE)[15]来分离监督的源信号。随后，Subakan等人[16]提出利用生成对抗网络(Generative Adversarial Networks， GAN)解决单通道盲去卷积的问题，将生成对抗网络应用于语音分离，目的是产生清晰的人声。然而，这些方法中混合矩阵是已知的，而且需要混合矩阵和与源信号满足相同的分布以便于进行训练。针对这个问题，Kong等人[17]提出一种基于深度卷积生成对抗网络(Deep Convolutional Generative Adversarial Networks， DCGAN)的合成分解(Synthesizing-Decomposition， S-D)方法，在源信号和混合矩阵未知的情况下，结合生成对抗网络来解决单通道混合信号的分离和去卷积的问题，但仅针对2路源信号的解混问题， 并不适用于分离多路源信号。

在汉字验证码的认证、数字水印、汉字图标中，经常出现汉字被遮挡或无法识别的现象，容易造成干扰。针对以上问题，本文提出了一种单通道盲去卷积的算法，以解决多路源信号的分离和去卷积问题。实验中将汉字和遮挡图像作为源信号，随机选择4路源信号进行卷积混合并分离出汉字图像和遮挡图像以证明该方法的有效性。本文的贡献主要有：

(1)提出一种单通道盲去卷积模型，适用于从单路混合信号中进行源分离和去卷积。该模型根据信号卷积的特点，将多路相互独立的源信号通过卷积方式进行混合(噪声可作为源信号)。

(2)提出一种新的单通道盲去卷积的算法，用于解决多路源信号的分离和去卷积问题。该算法基于优化的深度卷积生成对抗网络(Optimized Deep Convolutional Generative Adversarial Network，ODCGAN)，并将多路源信号的分离和去卷积的问题转成贝叶斯最大后验估计(Maximum A Posteriori estimation， MAP)问题，通过重构混合物的最小误差可以同时估计出多个源和混合矩阵。不断进行初始化选择出最优的结果，并结合l1范数与l2范数对源和混合矩阵进行优化来改善不确定混合信号的分离和去卷积的性能。

(3)提出一种多源信号计算均方误差(Mean Squared Error， MSE)损失的方法。该方法考虑每一种可能的信号分离的排列方式。4路源信号的排列方式共 24 种(两路源信号时仅有两种排列方式)，比较最小的MSE 损失并记录对应的分离出的源信号的顺序。

2 单通道盲去卷积模型

单通道盲去卷积过程中只有1路观测信号可用，从中解卷积出独立源信号和混合矩阵。先前的模型只针对2路信号，但对于2路以上信号的分离和去卷积问题未曾涉猎，本文要解决的问题就是通过单通道盲去卷积算法分离和解卷积出多路源信号。

卷积混合信号考虑了源信号的延迟，在不单独考虑噪声的情况下(噪声可作为源信号处理)，假设单个接收传感器接收到的混合信号X(t)是源信号s(t)和混合矩阵F(t)通过卷积混合得到的，则单通道盲源分离的卷积模型可表示为

3 SCBDC算法

3.1 最大后验估计

在本文的图像盲去卷积中，主要做了两步工作：第1步：将式(1)中的问题转化为贝叶斯参数估计问题。首先利用优化的深度卷积生成对抗网络对图像进行预训练；第2步：在汉字与遮挡图像的单通道盲去卷积过程中，不断进行不同的初始化选择出最优的结果，并利用adam优化器对源和混合矩阵进行优化选择最小误差来获得目标源和混合矩阵。将U设置为si和Fi的集合，即U= {s1，s2， ··· ，sM，F1，F2， ···，FM} 表示为需要估计的一组源和混合矩阵。可以通过最大后验估计MAP法来获取估计的源和混合矩阵U¯

3.2 ODCGAN原理

生成对抗网络基于对抗训练的原理，使用随机噪声生成图片，包含两个模型：一个生成模型，一个判别模型。生成模型的目的是利用生成器(Generator， G)生成假的图片，判别模型(Discriminator，D)是用判别器判断给定的图片是真实的图片还是生成器生成的图片，这两个模型一起对抗训练，最终达到一个稳定状态。ODCGAN的原理和GAN是一样的，只是把 GAN的生成器和判别器换成两个CNN，CNN具有很强的特征提取功能，将CNN引入到GAN的生成模型中做无监督训练可以提高生成模型的学习效果。并且，ODCGAN对CNN的结构做了一些改变，以提高图片的质量和收敛的速度，主要改变有：

(1)取消了原有CNN中的特征提取层即池化层，生成器中使用转置卷积层，判别器中使用卷积层，并在最后一层中加入全连接层；

(2)网络中使用归一化(Batch Normalization，BN)，可以稳定地学习，有助于解决初始化不合理导致的训练问题；

(3)生成器中激活函数用ReLU，最后一层用sigmoid，判别器中的激活函数用LeakyReLU，最后一层也用sigmoid。

其损失函数可表示为

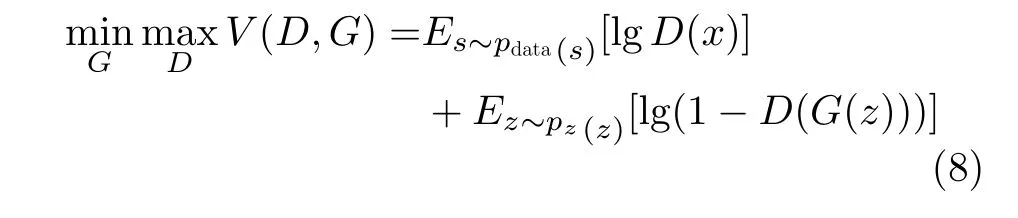
pdata是真实数据的分布，pz是生成数据的分布。

将网络训练的迭代次数设置为15000，生成器和判别器将进行迭代训练，并通过降低生成器的梯度，升高判别器的梯度来优化网络，如果训练成功，则生成的源信号的分布将收敛到pdata。ODCGAN的训练在表1中显示。

表1 SCBDC算法

3.3 优化估计

使用表1中的算法对源信号和混合矩阵进行优化，并重复m次，以解决局部极小值的问题，并选择具有最小重构误差的结果进行源信号的分离和去卷积。

4 实验

在本节中，将通过基于优化的深度卷积生成对抗网络的单通道盲去卷积(SCBDC)算法来解决不确定的源分离和解卷积问题。本文在由不同字体不同形态组成的汉字与遮挡图像数据集实验上进行了测试，随机选择4路信号进行混合。并从混合物中分离出目标源和混合矩阵， 以测试所提方法的有效性。图1为部分汉字与遮挡图像数据集样本。

图1 部分汉字及遮挡数据集

4.1 ODCGAN预训练

本文实验中利用优化的深度卷积生成对抗网络建立了生成模型，训练数据共20150张图片，测试数据共5650张，训练与测试数据中的图像具有相同尺寸大小为28 × 28。选择来自高斯分布的噪声输入样本，高斯分布的区间为[0， 1]，维数为100。生成器由4个转置卷积层组成并具有512， 256， 128和1的特征图，转置卷积层之后，应用归一化和ReLU非线性激活函数进行处理，ReLU激活函数的功能是防止梯度消失，最后一层使用sigmoid激活函数。判别器中最后一层加入了完全连接层，其他层使用LeakyReLU激活函数，最后使用sigmoid激活函数，并通过adam优化器对信号源和混合矩阵进行优化，这里将优化器的学习率设置为0.01。

本文在训练过程中进行了15000次迭代预处理，并保存结果和图片路径，为下一步的源分离和去卷积做准备。

4.2 图像盲去卷积

在本文的基于ODCGAN的汉字与遮挡图像的单通道盲去卷积实验中，研究的是4路信号的混合和分离，混合矩阵和单独的源信号都可以估计出来。从汉字数据集与遮挡数据集中随机选择数据，每组数据由4路单独的随机信号和混合矩阵混合成1路信号，图2随机显示了6组SCBDC算法进行单通道盲去卷积的结果，其中X表示混合信号，s1，s2，s3，s4表示初始的4路源信号，s¯1，s¯2，s¯3，s¯4表示对应估计的信号。F1，F2，F3，F4表示初始的4路混合矩阵，F¯1，F¯2，F¯3，F¯4表示对应估计的混合矩阵。从图中可以看出，针对4路信号的分离和去卷积问题，本文所提出的单通道盲去卷积算法在很大程度上都可以较好地估计出源信号和混合矩阵，证明了该方法的有效性。

图2 SCBDC 方法进行图像盲去卷积的结果

图3展示了本文所提算法与S-D算法[17]进行盲去卷积的结果(以两路信号为例)。

图3 S-D算法与SCBDC 算法进行图像盲去卷积的对比结果

4.3 评价

为了验证本文提出的基于ODCGAN的单通道盲去卷积算法的有效性，使用峰值信噪比(Peak Signal to Noise Ratio， PSNR)进行评估，PSNR越高，表示信号分离和去卷积的效果越好，跟真实信号越接近。并结合信号相关性来衡量分离出的信号与源信号的相似程度。

4.3.1 峰值信噪比

两张尺寸为a × b的图像之间的均方误差MSE可表示为

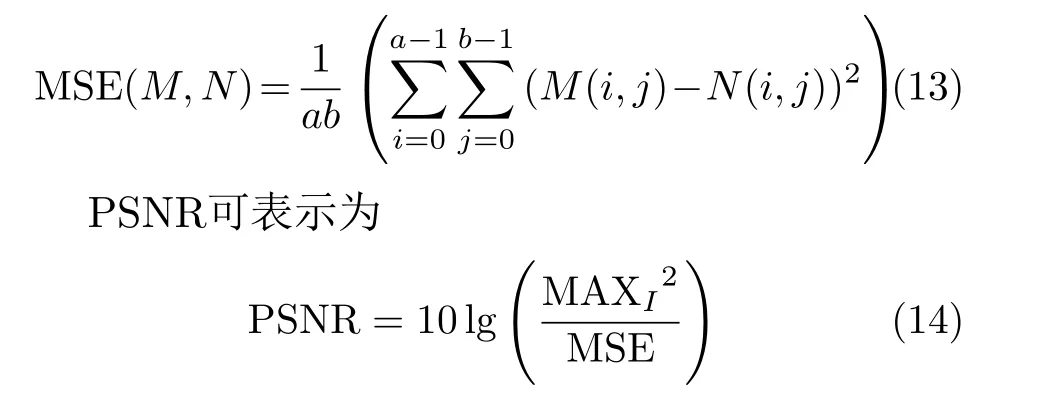
其中，MAXI代表无噪图像的最大值。

表2显示了本文中SCBDC算法进行4路源信号的盲去卷积过程中在不同初始化次数下所得到的PSNR值，可以看出50次初始化的 SCBDC方法具有比15次初始化和1次初始化获得更高的PSNR，并达到稳定。

表2 不同初始化的PSNR值(dB)

本文实验用相同的数据集，将SCBDC算法进行2路源信号盲去卷积所获得的PSNR与非负矩阵分解法NMF[18]和S-D[17]算法所获得的PSNR进行对比，结果如表3所示，本文所提的算法比NMF和SD算法具有更高的PSNR值。因此，针对2路源信号的盲去卷积问题，本文算法相比已有算法效果更好，而且可以处理多路源信号的盲去卷积问题。

表3 不同算法的PSNR值(dB)

4.3.2 信号相关性

信号的互相关是用来描述两个信号间的相似程度，信号x和y的互相关函数可以表示为

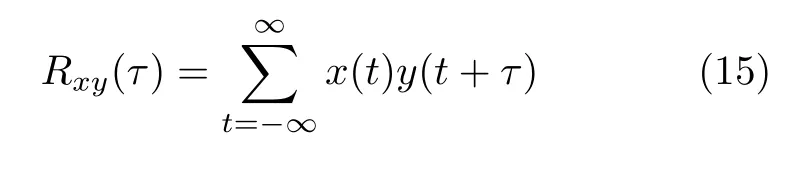
按照图2分离出的6组信号，表4显示了本文算法分离出的目标信号与源信号的互相关性取值，R的值越高，表示目标信号与源信号的相似度越高，则分离的源信号的质量越好。从表4可以看出本文算法在4路源信号的分离上所获得的目标信号与源信号的平均互相关性在整体上都较高。

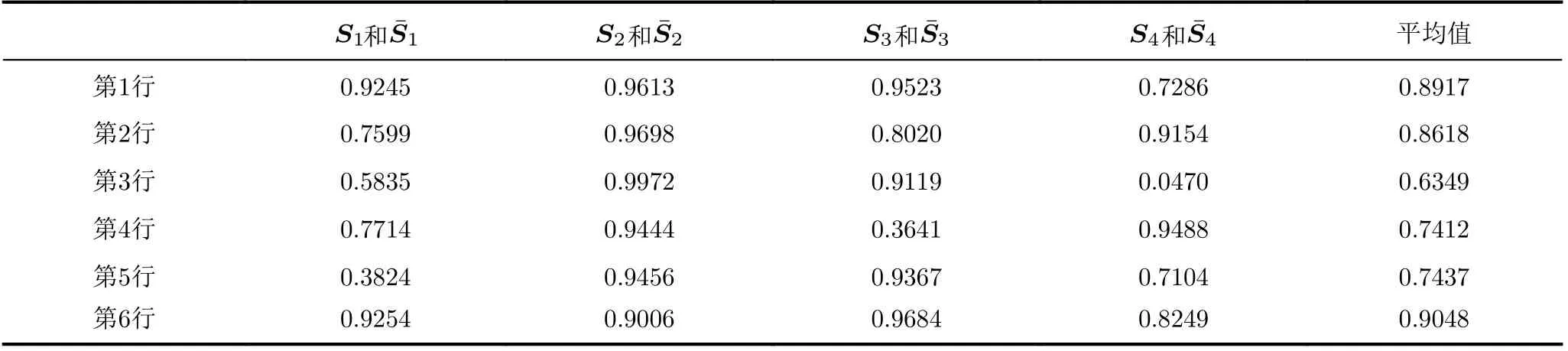
表4 目标信号与源信号的互相关性值

本文根据2路源信号的分离结果，对比了S-D算法与NMF算法所获得的目标信号与源信号的平均互相关性值，结果如表5所示。很明显，本文算法所获得的信号的总平均互相关性更高。

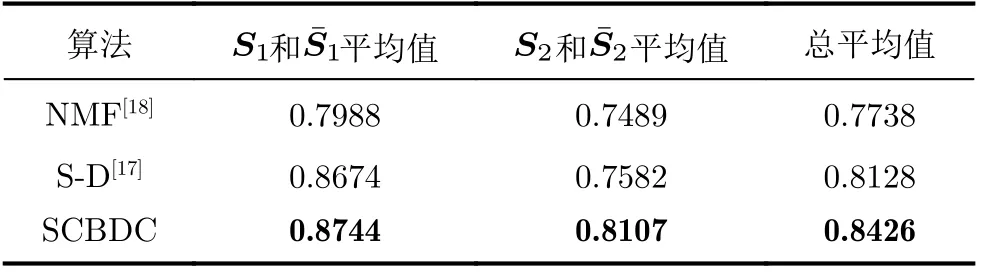
表5 不同算法的源信号与目标信号的平均互相关性值

5 结束语

本文提出了一种基于ODCGAN的单通道盲去卷积算法来解决多路源信号的分离和去卷积问题，利用优化的深度卷积生成对抗网络建立源信号的模型，对汉字与遮挡图像数据集进行训练，并将源信号的分离和去卷积问题转化为贝叶斯估计问题。在进行信号的分离和去卷积过程中，将混合物重构误差降到最小，并多次进行初始化选择最优的结果，提高不确定混合信号的分离和去卷积的性能。实验中随机选择4路信号进行混合，利用该算法分离出独立的源信号和混合矩阵，实现了10.4 dB的峰值信噪比，并结合相关度指标衡量信号分离的整体效果，体现了SCBDC算法在混合信号的分离和去卷积上的有效性。将来，我们将更多地考虑加入噪声，尤其是增卷积噪声以及考虑采用更好的方法提高单通道混合信号的分离去卷积的性能。