水流作用下斜桩局部冲刷及流场变化试验研究❋

王晓光, 程永舟,2❋❋, 罗 巍, 黄筱云,2， 吕 行

(1. 长沙理工大学水利工程学院， 湖南 长沙 410114； 2. 水沙科学与水灾害防治湖南省重点实验室， 湖南 长沙 410114)

桩基础形式中，垂直桩、斜桩、叉桩、复合桩基础是最为常见的结构形式[1]。斜桩水平承载力高、可充分发挥垂直承载力的特点，使其广泛应用于码头、桥墩等结构物建设中[2]。同时，植被密集的河口与岸滩中，倾斜的植物也可以用斜桩进行概化分析[3]。因此针对斜桩及其概化模型，开展相关研究对丰富水流-结构相互作用理论与工程实践都具有重要意义。

关于垂直桩的局部冲刷问题，早期学者进行了深入广泛的研究[4-7]。但是，对于斜桩冲刷及流场分析的研究开展较少。如图1所示，定义倾斜角度α为桩轴线与铅垂线的夹角。当桩向上游倾斜时为反斜桩，α<0；当α=0时为垂直桩；当桩向下游倾斜时为正斜桩，α>0。Breusers和Raudkivi[8]通过对变直径锥形桩的研究，认为桩轴线与垂线的夹角是影响冲刷的重要因素。Bozkus等[9-10]通过正斜桩试验，建立起α≤15°条件下倾角与相对冲刷深度之间的关系。Euler等[11]研究了孤立木本植物倾斜角度和渗透性对局部冲刷和泥沙沉积的影响。Vaghefi等[12]通过试验研究了桩径对于正斜桩冲刷的影响，并建立起倾角与最大冲深度减小率之间的关系。Zhao等[13]通过DNS三维模拟，分析了倾角对正斜桩尾涡流动、拖曳力系数、尾涡脱落频率的影响。Najaf等[14]利用PIV将正斜桩流场可视化，观察到相对于垂直桩完全不同的流动模式。Majd等[15]进行定床模型试验，分析了倾角与马蹄涡、尾涡、桩截面形态、上游分离点之间的关系。Kitsikoudis[3]采用动床与定床相结合的试验方法，建立起正斜桩冲刷特性与尾涡特性的关系。Du等[16]借助FLOW-3D软件搭建数值水槽，通过对正斜、反斜、侧斜桩的冲刷模拟和桩前水流分析，得出了桩前冲刷深度的排序。Liu等[17]使用OpenFoam开展低雷诺数下并列正斜桩的尾涡特性、间隙流动特性研究，进一步扩展了斜桩的研究范围和深度。

由上不难看出，学者们对正斜桩冲刷特性、力学系数、尾涡特性已进行了初步的研究。然而，与反斜桩相关的研究及报道较少。尤其是对反斜桩局部冲刷特性与垂直桩、正斜桩的差异比较缺乏深度讨论。本试验在水流作用下开展多种倾角斜桩的局部冲刷研究，初步分析了清水条件下反斜桩、正斜桩冲刷历时、最大冲刷深度、床面形态、桩后沿程流速分布与倾角的关系，重点探讨反斜桩、垂直桩、正斜桩冲刷及流场的差异，为相关工程设计提供理论依据。

1 试验布置及试验工况

1.1 试验布置

试验在长沙理工大学水利实验中心波流水槽中进行，试验布置如图1所示。水槽长45 m，宽0.8 m，高1 m，工作水深0.2～0.7 m。水槽设有循环造流系统并配备有沉淀池。试验沙槽位于水槽中部，长3 m，宽0.8 m，高0.6 m，内部铺满中值粒径d50=0.403 mm的无黏性沙。Chiew和Melville[18]指出，当桩径小于0.1倍水槽宽度时，水槽边壁效应可以忽略。因此，本试验斜桩模型采用直径D=5 cm的不锈钢圆管，埋置在沙槽中部，水流到达斜桩前可形成稳定的流速剖面。试验水深H=0.4 m，大于3～4倍桩径D，此时可忽略水深对于冲刷的影响[19]。试验中设置α为-30°、-20°、-10°、0°、10°、20°、30°共7种不同倾角的斜桩。试验断面平均流速V=0.21、0.23、0.26 m/s。采用Nortek公司生产的三维剖面流速仪(ADV)监测试验流速。采用加拿大2G Robotics公司生产的ULS-100型水下激光扫描仪，精准测量床面形态。

图1 试验布置图

1.2 试验方案

试验中倾角α=-30°、-20°、-10°的桩为反斜桩，倾角α=+10°、+20°、+30°的桩为正斜桩，0°垂直桩为对照组，试验共计7组21种工况。试验所采用的断面平均流速均小于泥沙临界起动流速，不发生上游输沙，所有工况在清水条件下进行。每次试验前先将沙床表面抹平，然后打开阀门往水槽中注水至试验水深0.4 m。随后启动造流水泵以计算机伺服系统控制电机加速过程，并以ADV流速仪实时观测，使流速稳步增加到试验流速。试验工况如表1所示。

表1 试验工况

计算公式如下[20]：

(1)

式中：V*c为剪切流速，由希尔兹曲线求得；Vc为泥沙临界起动流速，本次试验中Vc=0.347 m/s;d50为泥沙的中值粒径；H为水深。

2 试验结果与分析

2.1 冲刷历时及冲刷坑地形

图2为V=0.23 m/s时，-20°反斜桩、0°垂直桩、+20°正斜桩试验中桩前相对局部冲刷深度的历时曲线，曲线中的数据通过斜桩上的刻度尺读取。根据图2曲线特征，可将试验分为三个阶段，试验前期曲线斜率较大，相对局部冲刷深度发展迅速，100 min时能达到准平衡局部冲刷深度的70%以上。试验中期，曲线趋于平缓，冲刷速率逐渐减小，400 min时能达到准平衡局部冲刷深度的90%以上。进入试验后期，曲线接近水平，相对局部冲刷深度发展缓慢，可认为此时局部冲刷达到准平衡状态。在相同流速条件下，垂直桩局部冲刷速率及准平衡局部冲刷深度最大，反斜桩次之，正斜桩最小。所有试验工况进行至600 min，并记录600 min时斜桩桩前局部冲刷深度作为实测冲刷深度。

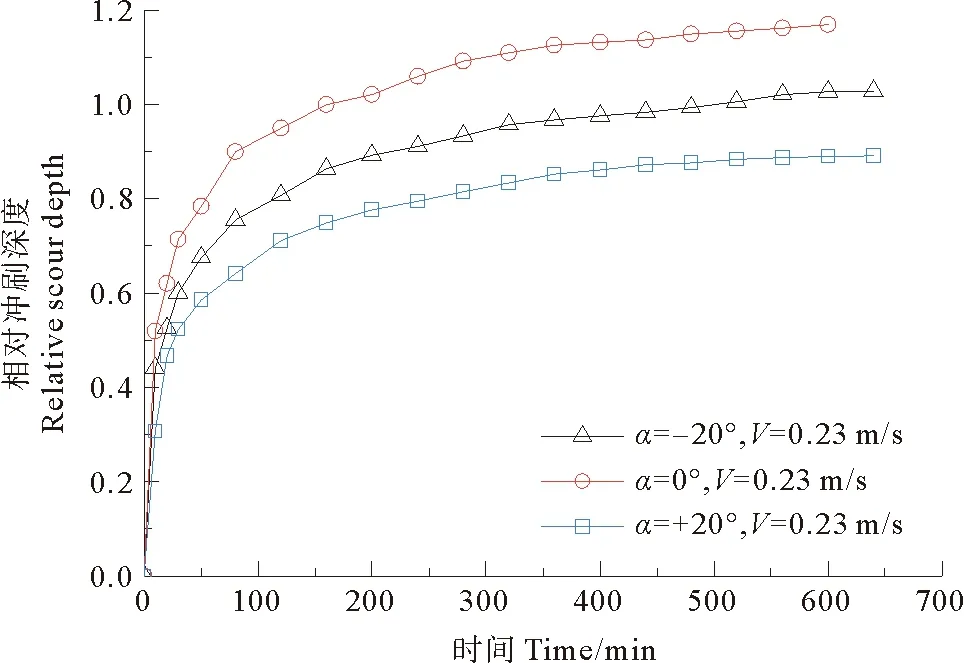
图2 桩前相对冲刷深度历时曲线

图3为V=0.23 m/s时，-20°反斜桩、0°垂直桩、+20°正斜桩的准平衡状态冲刷坑地形照片。将图3(a)、(c)与图3(b)对比可得，清水条件下斜桩附近的冲刷坑形态与垂直桩类似，呈现出规则的对称分布，主要由围绕桩前后连通的环状冲刷坑、桩后“马鞍状”沙丘、沿冲刷坑中轴线的沙脊组成，且最大冲刷深度的位置均在桩前。但斜桩的冲淤尺度均小于垂直桩。反斜桩与正斜桩的冲刷坑地形也有所差异。如图3(a)、(c)所示，反斜桩周围的沙丘和冲刷坑尺度更大，桩前角区空间较小，沙脊线陡峭且呈“S”形，桩后最大冲刷深度点距离后桩面更远。而正斜桩周围的沙丘和冲刷坑尺度较小，但床面形态更平滑，沙脊线更平缓。

图3 不同倾角下的冲刷坑地形

2.2 倾斜角度对冲刷坑剖面的影响

图4为V=0.21 m/s时不同倾角斜桩冲刷坑的特征剖面图。两个特征剖面的位置分别为平行于水流方向过桩中心点的纵剖面、垂直于水流方向过桩前最大冲刷深度点的横剖面。冲刷坑特征剖面的测量采用水下激光扫描仪，测量全过程在水下进行。

对于反斜桩，由图4(a、b)可以观察到在相同水流条件下，随着倾角的增加，冲刷坑的深度、宽度及沙丘高度均逐渐减小，沙丘位置逐渐向来流方向移动。而图4(a)显示各倾角反斜桩冲刷坑侧壁面之间位置相对较远，冲刷坑横向宽度变化较大，倾角主要影响的是反斜桩冲刷坑横向宽度的变化。图4(b)显示，各倾角反斜桩的冲刷坑前壁面形态一致且位置较近，桩前冲刷坑长度基本不变。说明冲刷坑侧壁面是反斜桩局部冲刷泥沙的主要来源。由图4(c、d)可以观察到，正斜桩冲刷坑及沙丘的尺度随着倾角的增加明显减小，逐渐表现出与垂直桩不同的形态特征。主要体现在桩后沙丘高度逐渐递减，沙丘坡度变缓且位置向来流方向移动，沙丘形态如图3(c)所示呈“流线型”。不同倾角的正斜桩冲刷坑大小相差较大，说明倾角的变化显著影响了正斜桩前壁面与侧壁面的冲刷程度，冲刷下来的泥沙在水流的作用下，搬运到桩后堆积成沙丘[12]。因此正斜桩同垂直桩一致，前壁面和侧壁面是局部冲刷泥沙的主要来源。

图4 倾斜角度对冲刷坑剖面形态的影响

相对于垂直桩，随倾角的增加，正斜桩、反斜桩的局部冲刷坑深度及冲刷坑大小均有不同程度的减小，对应的桩后沙丘高度也随之减小，即斜桩局部冲刷较垂直桩明显减弱，且正斜桩局部冲刷的减弱程度大于反斜桩。

2.3 倾角对床面附近沿程流速分布及湍流的影响

定义当斜桩床面附近的回流区纵向长度达到最大值时所对应的倾斜角度为临界角。由图5可以观察到从α=-30°至α=+30°沿程水平流速分布呈现逐步发展的趋势，桩前沿程流速梯度逐渐减小，曲线趋于平缓。而桩后流速分布则较为复杂。由于回流区的影响，桩后有明显的负向流速。对于垂直桩，在X/D=-1.65处流速由负变为正，随后流速逐渐增大。对于反斜桩，当α=-10°时桩后流场紊动较为剧烈，在反斜桩中达到最大，且水平流速需要较长的距离才能恢复正值。随着反向倾角继续增大，桩后沿程流速分布趋向稳定且负向流速区长度也更大，说明回流区在床面附近(Z/D=1)的纵向长度也随之增大。α=-30°时其回流区长度达到1.4D，但是负向流速较小回流减弱。而正斜桩则呈现出与反斜桩不同的变化趋势，α=+10°时桩后沿程流速相对于垂直桩紊动更大，速度恢复到正值所需的距离也更大。随着正向倾角的继续增大，桩后流速紊动减弱，流速由负变正所需的距离减小。因为正向倾斜角度越大，回流区范围越小，速度耗散越小，在近床面附近流速恢复到正向所需的距离越小[3]。但倾斜角度对于减弱回流区纵向长度及强度的现象必须达到临界角后才表现出来，这与Majd等[15]和Kitsikoudis等[3]所观察到的现象一致，对于临界角的具体值有待进一步深入研究。

为了进一步确定该现象的正确性，选取图5中受倾角影响较大的点(X/D=-1)作为参考点，得到该点湍流强度随倾角变化,如图6所示。可以明显观察到urms和wrms变化趋势一致，且极值点所对应的倾斜角度也相同。而vrms与urms、wrms变化趋势则较为不同，当urms和wrms达到极大值时，vrms为极小值，当urms、wrms达到极小值的时候，vrms为极大值。同时还可以观察到当α=±10°时，urms、wrms取得极值，且值大于垂直桩结果；当α>+10°或α<-10°时反斜桩与正斜桩水平和垂向的湍流强度均小于α=±10°时所对应的湍流强度值，这与水平时均流速分布所呈现的规律一致。

图5 沿程流速分布与倾斜角度的关系(Z=5 cm)

图6 湍流强度与倾斜角度的关系(Z=5 cm)

2.4 倾角及流速对冲刷深度的影响

由表2可知，正斜桩与反斜桩的桩前局部冲刷深度均较垂直桩有明显减小。当V=0.23 m/s、α=30°时，正斜桩冲刷深度相对于垂直桩减小36.8%，反斜桩减小20.5%。当V=0.26 m/s、α=30°时，正斜桩冲刷深度相对于垂直桩减小39.1%，反斜桩减小15.2%。在同为V=0.21 m/s、α=30°的条件下，正斜桩比反斜桩冲刷深度多减小27.8%。因此在斜桩的工程设计中，考虑桩的倾斜方向与水流方向一致时趋于安全。

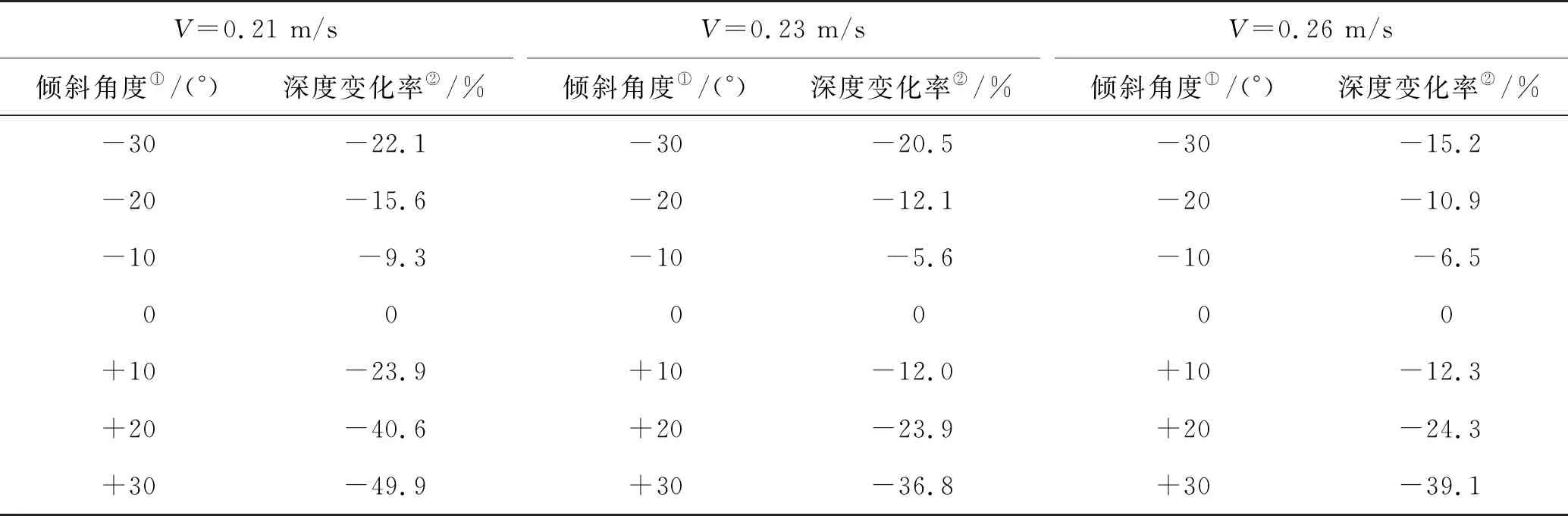
表2 最大冲刷深度变化率

图7(a)为三种不同流速条件下，桩前相对冲刷深度随倾角变化的曲线。图7(b)为不同流速条件下，桩后沙丘相对堆积高度随倾角变化的曲线。由图7(a)、(b)对比可知，桩前相对冲刷深度和桩后沙丘相对堆积高度随倾角的变化有类似趋势。这是因为所有试验工况中V/Vc<1，即冲刷处于清水冲刷状态，桩柱上游不发生泥沙的起动与输移，桩周的泥沙在马蹄涡及下降水流的作用下被水流挟带到桩后堆积形成沙丘。于是当冲刷深度大时，沙丘高度对应也较大。这种规律对于清水冲刷条件下的反斜桩、垂直桩和正斜桩均适用。

图7 冲刷深度及沙丘堆积高度相对值随倾角变化图

2.5 倾角与相对冲刷深度之间的关系

图8为本试验与Bozkus等[10]、Du等[16]、Kitsikoudis等[3]的数据对比图。为了分析倾角α与相对冲刷深度S/D之间的关系，将相对冲刷深度S/D与倾角α进行线性回归分析得到斜率和相关指数R2。反斜桩数据的回归曲线斜率为0.007 28±0.000 62，相关指数R2≥0.869 9，线性回归效果良好。这表明倾角和反斜桩相对冲刷深度之间存在较好的线性关系。正斜桩各回归曲线的斜率差别相对较大，但相对冲刷深度随倾角的增加而减小的趋势保持一致，且相关指数R2≥0.891 2，线性回归效果更好。因此，倾角和斜桩的桩前相对冲刷深度之间具有较好的线性关系，但不同试验的线性系数存在差异。并且，相同试验条件下反斜桩斜率的绝对值总小于正斜桩，即随着倾角的增加，正斜桩相对冲刷深度减小更快，与本试验结果保持一致。

图8 桩前相对冲刷深度数据对比

2.6 斜桩冲刷深度经验公式拟合

之前有学者已经提出了正斜桩冲刷深度的预测公式，但大多是针对于水深较小(H/D<4)的情况，且未给出反斜桩的预测公式，因此针对倾斜角度与相对冲刷深度之间较强的线性关系，提出折减系数K0对Melville等[20]纯流条件下垂直桩的预测公式进行修正，从而得到预测反斜桩与正斜桩冲刷深度的经验公式：

(2)

式中：KI为水流强度；Ky为水深桩径比；Kd为桩径泥沙粒径比；Kσ为泥沙级配；Ks为形态系数；Kα为校正系数，具体计算方法见Melville等[20]所给定的方法。倾斜角度与斜桩冲刷深度之间具有较好的线性关系，但在不同流速条件下斜率又有所差异，因此确定折减系数为相对流速和倾斜角度的函数。首先对V/Vc和α进行求对数和求正弦值预处理，随后进行拟合得到折减系数K0的计算公式如下：

(3)

式中：a、b、c、d、e为拟合参数，具体取值见表3；V/Vc为相对流速;α为倾斜角度。

表3 拟合参数

图9为本试验和Du等[16]的反斜桩、正斜桩数据与预测公式(2)计算值的对比图，可以观察到经验公式可以对反斜桩、正斜桩的冲刷深度进行很好的预测，误差在±20%以内。

3 结论

本试验研究了恒定水流作用下，倾角、流速对于反斜桩、正斜桩冲淤及流场的影响，并重点与垂直桩特性进行对比，分析了倾角与相对冲刷深度、桩后回流区特性之间的关系，可以得到如下主要结论：

(1)在相同水流条件下，斜桩桩前最大冲刷深度随着倾斜角度的增加逐渐减小，且正斜桩减小速率大于反斜桩减小速率。

(2)随着倾角的增加，斜桩冲刷坑形态逐渐展现出与垂直桩不同的特征。正斜桩沙丘高度逐渐递减，坡度趋于平缓且位置向来流方向移动，而反斜桩该现象不明显。相对于反斜桩和垂直桩，正斜桩更符合“流线型”结构，桩前冲刷深度衰减更明显。

(3)在0～±30°范围内，斜桩桩后流场相对于垂直桩明显不同。对于反斜桩，当倾斜角度达到临界角后，倾角的继续增大会使得床面附近回流区的纵向长度变大，紊动减弱。而对于正斜桩，倾角的继续增大会使近床面附近回流区纵向长度减小。

(4)斜桩桩前相对冲刷深度与倾斜角度之间具有较好的线性关系，但不同试验的线性系数存在差异。根据试验数据拟合出预测斜桩冲刷深度的经验公式。