基于IOWA算子的我国居民消费水平组合预测研究

李 颖， 庄科俊

(安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)

0 引 言

目前，对于非负变权重组合预测模型在理论与应用两方面的研究比较丰富。在组合预测模型的非负权重研究方面，由Bates和Granger[1]首次提出组合预测模型的概念，通常将他们所提出的最小方差组合预测模型简称为B-G组合预测模型。但是，根据B-G组合预测模型所选取的最优权重可能会产生具有负分量的权系数向量，负的权重分量可能是由组合预测模型存在的多重共线性导致的，又由于对负权重经济含义的解释存在争议，因此，很多学者建议加上非负权重约束条件。如孔庆凯、唐小我[2-4]等一批学者在组合预测模型规避负权重方面提出了简单平均加权法、均方差倒数加权法和二项式组合预测方法等，推动了组合预测模型在非负权重领域的迅速发展。组合预测模型在变权重领域的研究方面，由于传统的组合预测模型赋予单个预测模型在所有观察期内都相同的权重，可能会出现单个模型在某一观察期预测精度高却在另一观察期预测精度低，从而导致预测精度不一致的问题。显然，如果给单项模型赋予固定权重，就会导致预测精度不高、预测误差较大等。自21世纪以来，很多学者开展了对变权重组合预测模型的深入研究。陈华友等[5]发现有序加权平均(OWA)算子组合预测模型有很大的缺点，因此他引出诱导有序加权平均(IOWA)算子的概念，并将此概念应用于预测企业所得税，调查结果显示诱导有序加权平均(IOWA)算子能够增加组合预测的精度。在预测我国居民消费水平的研究方面，宋峰等[6]以GM(1,1)模型、线性回归模型以及时间序列模型为基础，构建组合预测模型，预测2010—2012年安徽省城镇居民人均消费；侯甜甜等[7]通过建立ARIMA模型预测我国CPI的变化趋势，并且以主成分分析法所确定的影响我国CPI的主要因素作为解释变量建立多元线性回归模型;张甜瑞[8]通过对2000-01—2019-08的月度数据建立ARIMA(2,1,2)×(1,1,1)模型，预测未来一年陕西省的CPI，并且把最后8期数据作为参照用于检验模型的预测精度，得出陕西省的居民价格指数不会存在剧烈波动。

综上所述，对IOWA算子组合预测模型的理论与应用研究较为成熟，但是关于预测我国居民消费水平的论文大多采用一种预测模型，或是采用赋予单个模型固定权重的组合预测模型，大多使用单项预测模型的论文都无法对预测模型的有效性进行检验。因此，本文根据ARIMA(2,1,1)模型、Holt-Winters无季节模型和多元回归模型，主要是利用有序加权算术平均IOWA算子组合预测模型，预测中国在接下来的4年内(2020—2023年)居民消费水平，并构建模型的有效性评价体系。在新发展格局下，以内循环与外循环为依据寻找“双循环”的解释变量构建多元线性模型，使得对未来几年的居民消费水平预测具有更大的参考价值与实际意义。

1 模型简介

1.1 IOWA算子

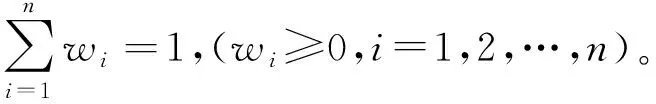
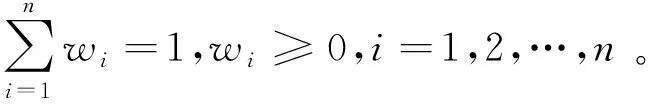
显然，IOWA算子是对(α1,α2,…,αn)诱导因子按照降序排序后所对应的(β1,β2,…,βn)值进行有顺序的加权平均，因此赋予各单项模型在每一时点上的权重与诱导值的大小无关，而与诱导值的相对大小即排序有关。

1.2 IOWA组合预测模型

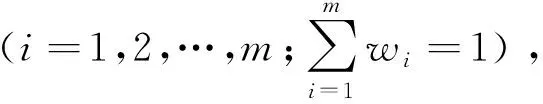
本文采用预测精度作为诱导因子，如果诱导因子αit(i=1,2,…,m；t=1,2,…,T)选择第t期用第i种预测方法的预测精度，则αit的表达式为

对诱导因子所生成的m个二维数组(<α1t,x1t>,<α2t,x2t>,…,<αmt,xmt>)按照诱导因子的降序排列，根据误差平方和最小准则求得各精度的权重系数向量为

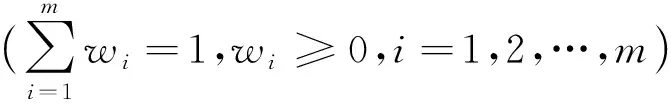
由预测精度α1t,α2t,…,αmt所生成的x1t,x2t,…,xmt，(t=1,2,…,T) IOWA算子组合预测模型预测诱导预测误差：eα-index(it)=xt-xα-index(it)(i=1,2,…,m；t=1,2,…,T)。

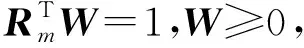
模型的总预测误差平方和为

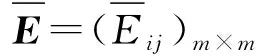
1.3 模型评价体系

建立IOWA算子组合预测模型评价体系所使用的误差和平均精度如表1所示。

表1 误差评价体系Table 1 Error evaluation system

2 实证分析

2.1 数据选择与数据来源

用人均消费支出(const，元)衡量被解释变量。选取2002—2019年我国人均消费衡量我国居民消费水平，变化趋势如图1所示。根据贾康与刘薇[9]在加快形成新发展格局的政策建议中所提到的把握新发展格局的要领，把解释变量分为内循环变量与外循环变量，分别选择人均可支配收入(dpit，元)和实际利用外商直接投资金额(fdit，万美元)。根据于佳茹[10]对我国居民消费水平的研究中所采取的变量，选取控制变量分别是国内消费税(taxt，亿元)、恩格尔系数(egct，%)。对于数据缺失值采用邻近值填充法。数据均来源于中国统计年鉴。

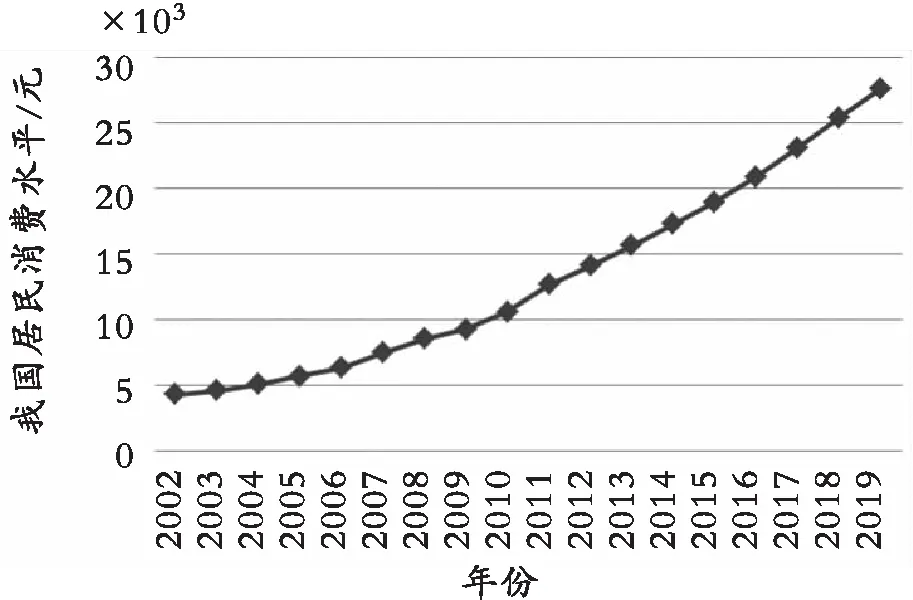
图1 居民消费水平的变化趋势Fig. 1 The variation trend of resident consumption level

2.2 变量的定义与描述性统计

对非平稳数列进行取对数以及取差分得到平稳数列(表2)。

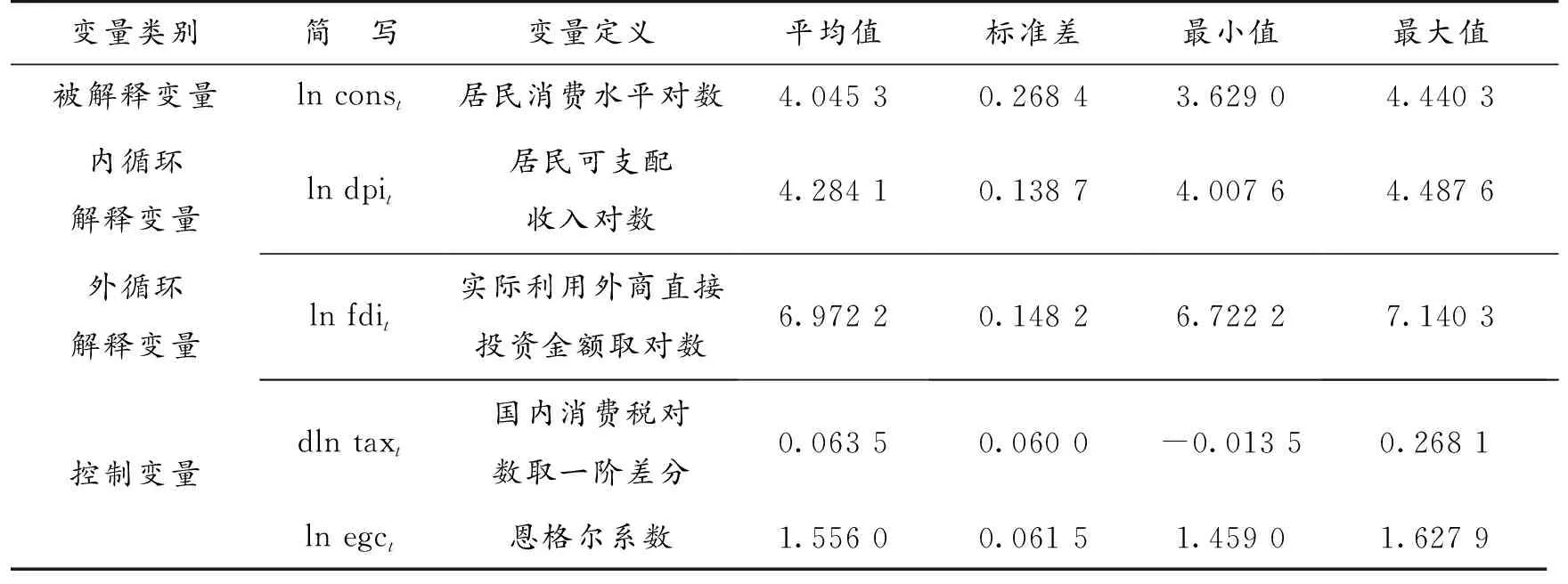
表2 变量的选取与基本特征Table 2 Variables and their basic characteristics

2.3 单项预测模型

2.3.1 ARIMA预测模型

将1990年到2019年间我国居民消费水平的年度数据作为样本，采用ARIMA模型对未来4年的人均消费进行预测，对ln cons做ADF检验，如表3所示，得到1阶差分时P值为0.034 3,小于0.05,所以ARIMA(p,d,q)中的d取1。对ln cons做自相关与偏自相关分析可得：由偏自相关图知此模型的滑动平均项的项数为2，由自相关图可知该模型的自回归项数为1,故ARIMA(p,d,q)中的p值选2，q值选1。而伴随概率P<0.05的 Q统计量可以判断此序列不是白噪声序列。最终确定选择ARIMA(2,1,1)模型，用ln cons对AR(1),AR(2)，MA(1)进行回归可知，该ARIMA(2,1,1)模型为

ln const=3.704 7+1.887 5ln const-1-0.894 1ln const-2+

(6.946 5) (22.296 67)

εt+0.458 9εt-1

(-10.801) (2.401 56)

D.W.=1.993 487F=3 965.054

由ARIMA(2,1,1)模型的残差序列白噪声检验可知该序列是较为稳定的序列。而伴随概率P>0.05的最右侧的Q统计量可以表明是白噪声序列。查表得在1%的上下界中，dL=1.01,dU=1.42，dU=1.42≤D.W.=1.993≤4-dU=2.58，故该模型不存在自相关。根据该模型的t值、P值都显著，拟合优度较高以及残差序列为白噪声可知该模型拟合得很好。

2.3.2 Holt-Winters无季节指数平滑模型

该模型是能够预测无四季变化但是有时间趋势的一种时间序列数据，Holt-Winters无季节指数平滑模型如下：

at=αyt+(1-α)(at-1+bt-1)
bt=β(at-at-1)+(1-β)bt-1

2.3.3 多元回归模型

考虑我国居民消费水平和居民人均可支配收入、实际利用外商直接投资以及国内消费税和恩格尔系数都是时间序列，对非平稳数列取自然对数以及差分得到平稳数列，因此最终得到如下模型：

经检验：该模型的R2=0.994 4，表明模型拟合得较好，杜宾值为2.352 8，查表得在1%的上下界中，dL=0.71,dU=1.42，dU=1.42≤D.W.=2.35≤4-dU=2.59。

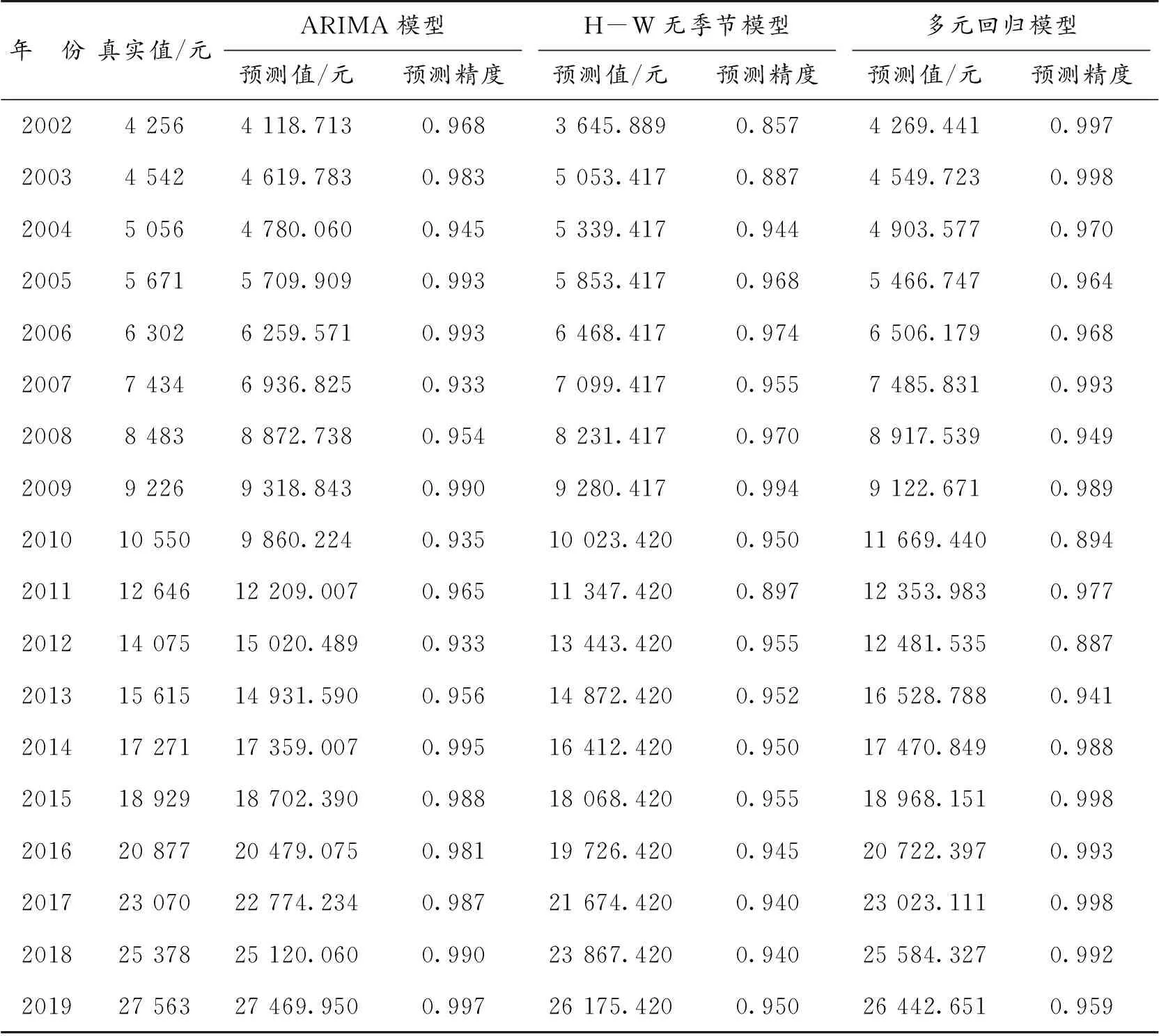
表3 单项模型的预测值与预测精度Table 3 Predicted values and prediction accuracies of single model

根据上述杜宾值，可以排除自相关对该模型的影响，由该模型的White Test的p值为0.614 9，大于0.05，可知该模型通过异方差检验，可以排除异方差对该模型的影响。因为大多数的VIF都大于1小于10，不存在全大于10或者小于1的情况，故该模型不存在多重共线性。内生性检验的P=0.618 3，且P>0.05,故可以排除内生性的影响。综上可知该模型拟合得较好。对该模型的ln dpi，ln fdi，ln egc 分别建立时间序列模型，运用静态预测的方法得到2020年至2023年的预测值，对dln tax进行Holt-Winters预测，得到2020年至2023年的预测值，在此基础上预测我国居民消费水平未来4年(2020—2023年)的值。

2.4 组合预测模型

2.4.1 模型的构建

构造的IOWA算子组合预测模型偏差平方和最低，具体思路如下：首先，按照预测精度的高低将各单项预测模型在每一时期的预测值进行重新排列，求出预测精度从高到低的误差大小；其次，构建误差分布表，求得模型的信息矩阵；最后，根据误差信息矩阵求得各精度预测值所占有的权重，并构建组合预测模型。

先按照预测精度的高低重新排列各单项预测模型在每一时期的预测值(表4)。

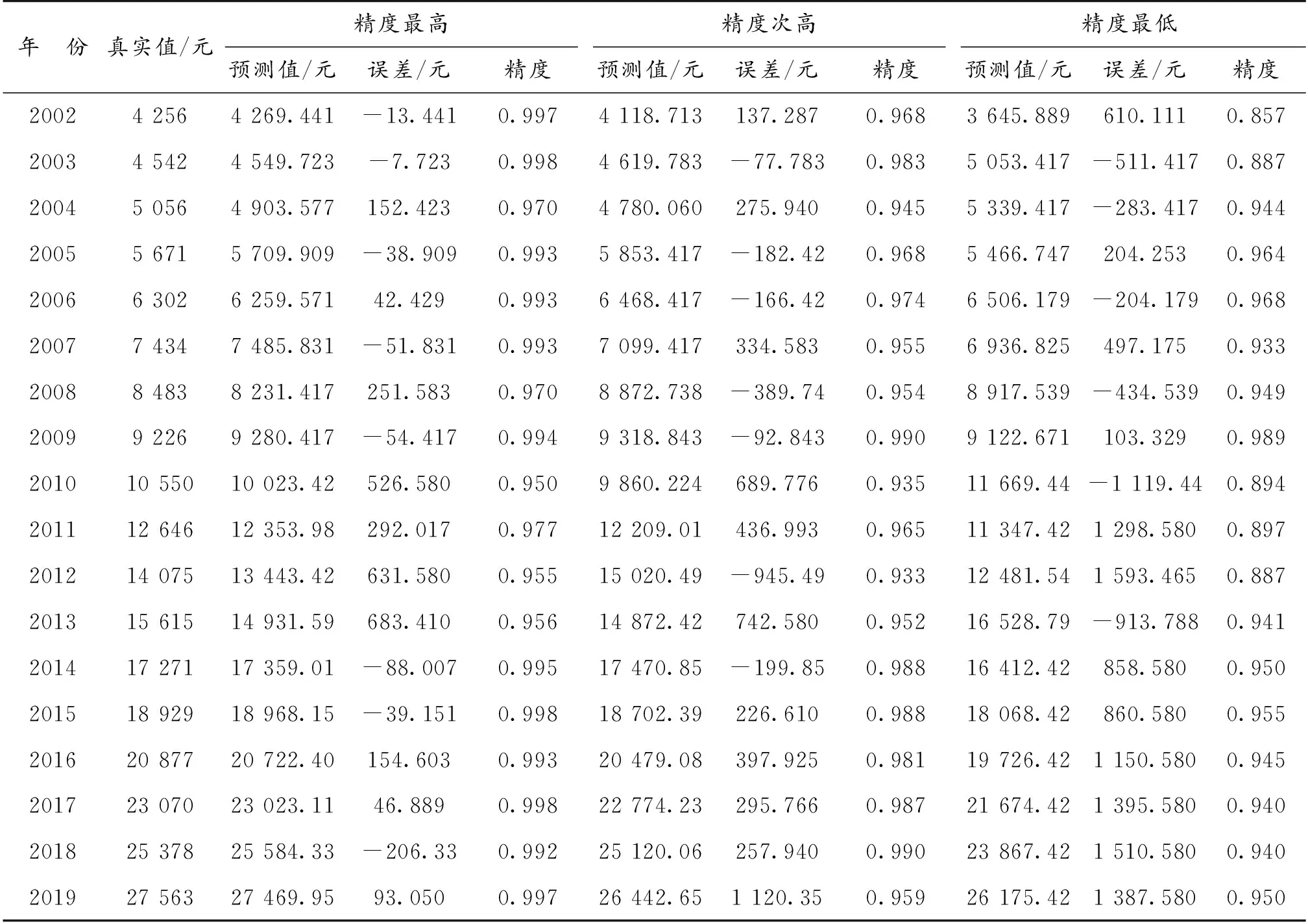
表4 按照精度由大到小排序的预测值与精度Table 4 The predicted values and precision are sorted from most to least in order of precision

其次，构建误差分布表，求得模型的误差信息矩阵为

E=

以误差平方和最小为目标建立(IOWA)算子组合预测模型为

即组合优化模型：

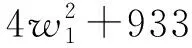
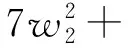
利用LINGO求解可得：

w1=0.759,w2=0.176,w3=0.065,U=1 148 140

最后，根据误差信息矩阵求得各精度预测值所占有的权重，并构建组合预测模型。根据该预测模型算出2002年到2019年我国居民消费水平(表5)。求得IOWA组合预测模型为

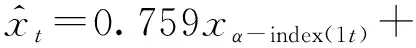
0.065xα-index(3t)(t=1,2,…,18)

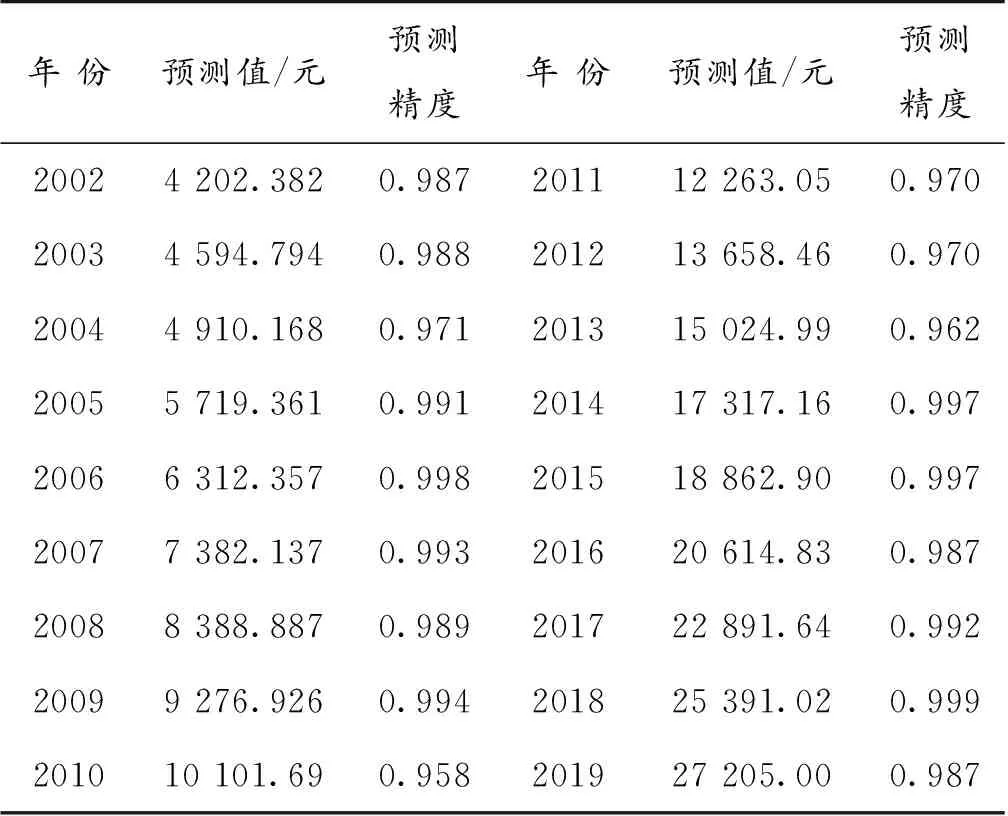
表5 组合预测模型的预测值Table 5 The predicted values of the combined prediction model

2.4.2 模型评价

用误差平方和最小的IOWA组合预测模型分别计算各项误差并进行归一化处理(与各种误差最大值进行比较，表6)。由表6可知，该组合预测模型的平方和误差只有Holt-Winters无季节模型的8.95%，平均绝对误差只有Holt-Winters无季节模型的25.63%，平均相对误差只有Holt-Winters无季节模型的26.25%，均方根误差只有Holt-Winters无季节模型的29.92%，均方根相对误差和均方百分比误差都只有ARIMA(2,1,1)模型的1.97%，平均精度高达98.5%。因此，用此组合预测模型对未来4年我国居民消费水平进行预测会具有较高的预测精度。

2.4.3 预测结果

IOWA组合模型对历史时期的预测是根据由实际值与预测值计算得出的预测精度进行诱导排序的，但未来的实际值并没有数据，故不能使用上文中求得的权重来预测未来4年我国居民的消费水平，故下面依据每一时期各单项预测模型在组合预测模型中所做出的贡献分配权重。对每一单项预测模型各期分配到的权重进行求和，用求得的各单项模型的权重之和除以18得到各单项预测模型对组合预测模型所做出的贡献。赋予ARIMA模型、Holt-Winters模型以及多元回归模型的权重分别为W1=0.332,W2=0.244,W3=0.424来预测未来4年我国居民消费水平(表7)。计算公式为

0.424xt-多元(t=19,20，…,22)

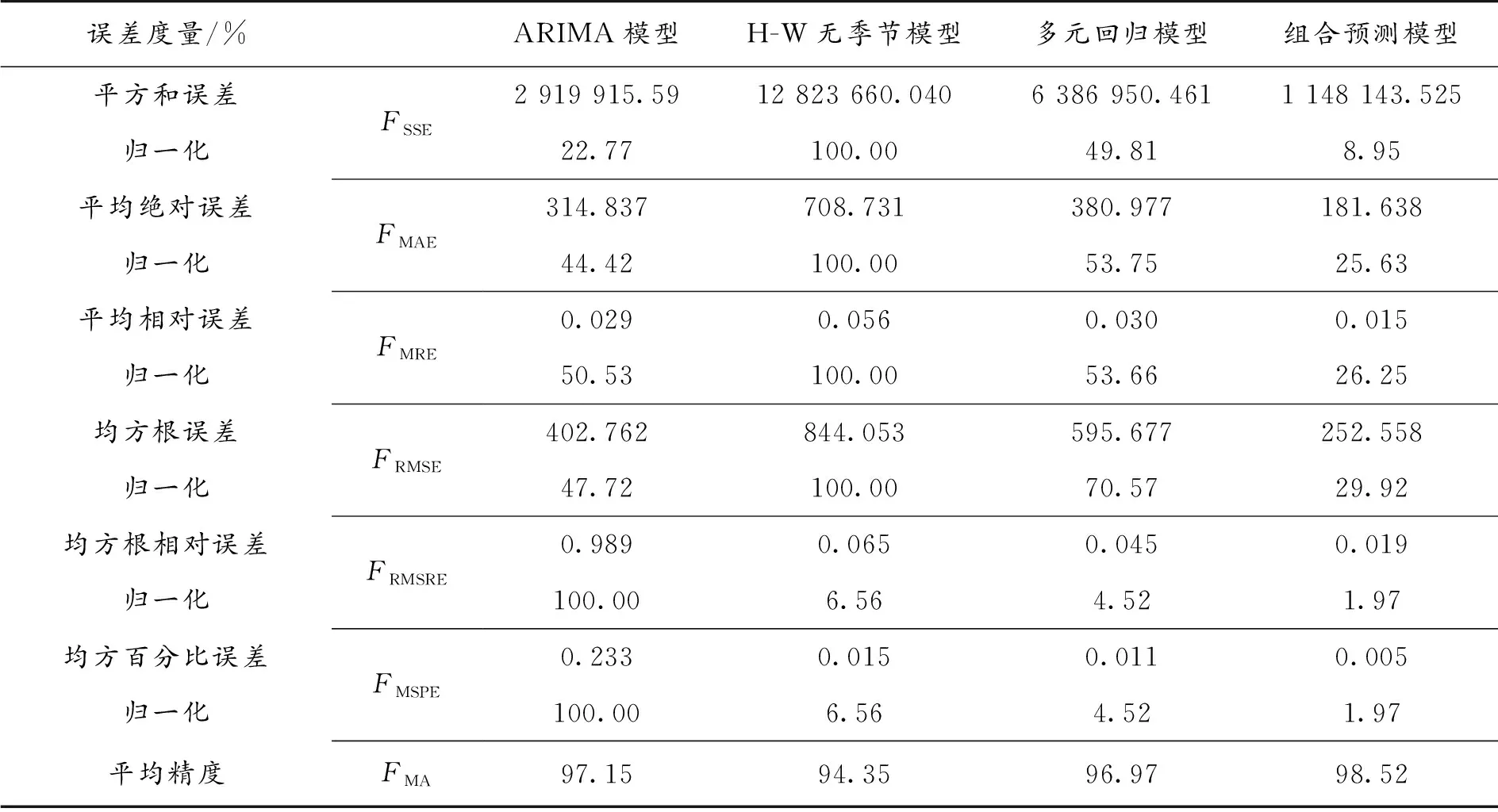
表6 各项模型误差比较Table 6 Error comparison of each model

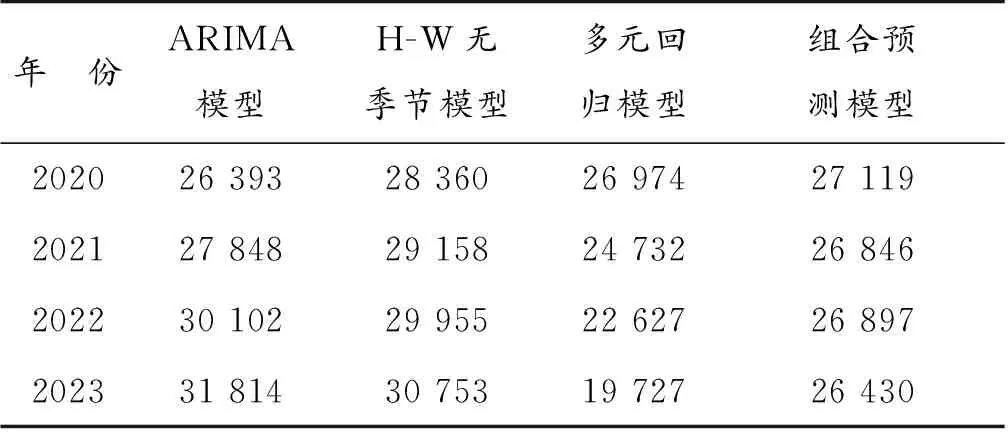
表7 各模型未来4年的预测值Table 7 The predicted values of each model in the next four years 单位：元

从预测结果来看，未来4年我国居民消费水平不会有大幅度的波动，将维持在26 000～27 000元的水平。

3 结 语

文章在开始处介绍了构建计算有序加权平均IOWA算子组合预测模型的相关理论内容，接着采用ARIMA(2,1,1)模型、Holt-Winters无季节模型和多元线性模型构建(IOWA)组合预测模型对未来4年的居民消费水平进行预测。其中多元线性回归模型把解释变量分为内循环变量与外循环变量，分别选择人均可支配收入和实际利用外商直接投资金额，控制变量选取的是国内消费税和恩格尔系数，用这4个变量来预测内循环与外循环对我国居民消费水平的冲击程度。

所构建的IOWA算子组合预测模型的步骤：首先，以各单个模型在每一年中的预测精度作为诱导因子，按照每年各单个模型的预测精度由大到小的顺序进行排序；其次，依据每一时期各单项预测模型在组合预测模型中的贡献分配权重，对每一单项预测模型各期分配到的权重进行求和，用上面求得的各单项模型的权重之和简单平均得到各单项预测模型对组合预测模型的贡献；最后，基于上一步中求得的权重建立组合预测模型，并对该模型进行评价。

最后研究结果表明：IOWA算子组合预测模型是文章提出的4种预测模型中具有最高精度、最低误差的模型。未来4年我国居民消费水平不会有大幅度波动，但有小幅度下降的趋势。未来4年我国居民消费的预测值分别是27119.279，26 846.191，26 896.611，26 430.128(单位：元)，变化幅度分别为-1.610%，-1.007%，0.188%，-1.734%。我国居民人均消费有微微下降的趋势，造成这种现象的原因可能是逆全球化的趋势，也可能是受到全球新冠疫情的影响。具体造成我国居民消费水平不增反而微微下降的原因有待进一步的深入研究。消费是推动经济发展的重要力量，应积极推进消费的正常增长，完善经济持续发展计划。