基于蜗壳损失模型的离心压缩机性能预测研究

张 波， 赛庆毅， 李 斌

(上海理工大学 能源与动力工程学院，上海 200093)

0 引 言

离心压缩机在国民经济各部门中占有重要的地位，特别在冶金、石油化工、天然气输送、制冷以及动力等工业部门获得广泛应用[1]。离心式压缩机设计的一个重要部分是在初步设计阶段能够准确地预测其性能。在初步设计阶段，性能预测可以模拟尚未制造的离心压缩机的性能，然后知道其性能参数是否满足设计指标的要求。性能预测还提供了多种选择的可能性，可以帮助设计人员优化机器性能，是设计高性能离心压缩机必不可少的工具。因此，在叶轮机械的初步设计阶段，性能预测可以缩短设计周期、降低设计成本、提高设计效率。

Galvas[2]率先利用叶轮和扩压器损失模型，针对离心压缩机叶轮入口段到扩压器出口段，进行了不同工况下的性能预测，结果表明效率和压比性能曲线的变化趋势与实验结果较吻合。损失模型在性能预测中非常重要，它决定了结果的准确性[3]，许多学者对离心压缩机的损失模型进行了大量研究，Jansen[4]、Aungier[5]、Coppage[6]、Daily[7]等对叶轮损失模型进行了研究，并提出损失模型；Aungier[5]、Stanitz[8]、李燕生[9]等提出扩压器损失模型。

对于同一个损失有多个损失模型，其适用范围也不尽相同。许多学者对损失模型的应用做了研究。Oh[10]针对4款不同的离心压缩机叶轮，对损失模型的选取进行了大量排列组合，通过与实验数据对比，提出了一种损失模型组合，用于预测离心压缩机的性能，同时还提出了一种改进的再循环损失模型。Elkin[11]通过4种损失的计算模型：3个间隙损失模型、4个轮阻摩擦损失、2个再循环损失模型和2个漏气损失模型，为预测设计条件下的单级离心压缩机等熵效率提出了合适的损失模型组合，但是在非设计条件下，不能很好地发挥作用。Zhang等[12]提出了一种通过根据叶轮进口叶顶相对马赫数和比转速，选择损失组合的方法。但是，以上研究均不包含蜗壳损失。

吴宝海等[13]基于损失模型，对离心压缩机进行了整机性能预测，通过与实验结果对比分析，以运行工况流量系数和设计工况流量系数比值作为修正因子，对叶轮尾流损失、叶轮分离损失和叶片扩压器进口冲击损失模型进行了首次修正，然后再对体积流量进行二次修正，修正后的预测结果能够比较准确地反映离心压缩机的性能。该修正方法的普及性有待验证，且文中的蜗壳损失模型系数需要从图上选取。闫雪等[14]针对带可调导叶的离心压缩机，同样以运行工况流量系数和设计工况流量系数比值作为修正因子，对叶轮摩擦损失模型、叶片载荷损失模型、尾迹混合损失模型和叶片扩压器损失模型进行修正，从叶轮入口到扩压器出口段进行了性能预测，修正损失模型后的预测结果更准确。相同地，滕庚等[15]针对超临界CO2离心压缩机，采用同样的修正因子，对叶片表面摩擦损失模型、叶顶间隙损失模型、尾迹混合损失模型、进口冲击损失模型、叶片载荷损失模型、回流损失模型、漏气损失模型和扩压器损失模型进行修正。发现修正后的损失模型能够有效提高预测精度，更好地预测压缩机的运行性能。通过对比发现，对于不同的离心压缩机，需要进行修正的损失模型不同，说明采用流量系数比值作为修正因子，修正损失模型的性能预测方法存在一定的局限性。

然而，以上讨论的性能预测方法并不包括蜗壳损失，并且对叶轮理论功也较少关注。蜗壳可能是离心压缩机级中容易被忽视的组件，但是为了收集扩散器或叶轮后面的气流并将其引导到压缩机后面的管道或冷却器，蜗壳是一个不可缺少的元件。蜗壳损失通常是根据传统的半经验损失模型来计算的，其缺点是计算结果有一个范围，使结果不准确，所以迫切需要一个能够比较准确计算蜗壳损失的模型。当谈及叶轮理论功时，滑移系数有着至关重要的作用，因此，有必要对滑移系数进行进一步讨论。

基于新的蜗壳损失模型和叶轮出口能量平均法，提出了一种新的单级离心压缩机性能预测方法，研究对象如图1所示。主要进行了以下工作：蜗壳损失模型的推导；采用能量平均法修正叶轮出口速度；实验和数值模拟验证、分析。

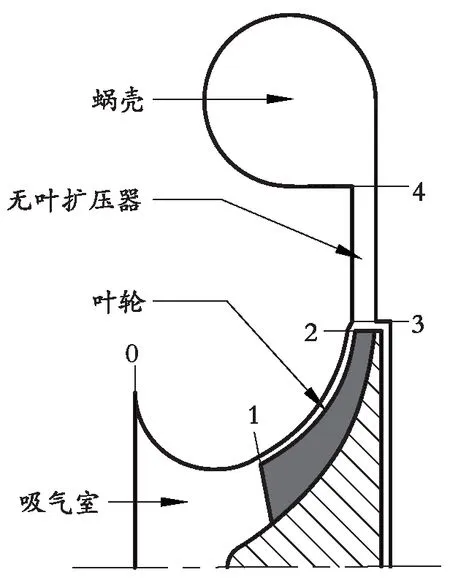
图1 离心压缩机示意图Fig. 1 Schematic diagram of centrifugal compressor

1 性能预测方法

性能预测是在无详细的叶片造型、流道尺寸的情况下，仅需要简单的一元设计参数，从理论功中扣除各通流元件的流动损失并忽略各元件间的相互影响，借助损失模型对机器进行性能数值模拟[16]。

将离心式压缩机按组成元件分为4个部分，以预测整个机器的性能，如图1和图2所示，包括吸气室、叶轮、无叶扩压器和蜗壳。相应地，离心压缩机的总损失可分为吸气室损失、叶轮损失、无叶片扩压器损失和蜗壳损失。如图1所示，定义了6个特征截面，截面0位于吸气室的入口；吸气室的出口即为是叶轮入口，截面1位于吸气室出口或叶轮入口；截面2位于叶轮的出口，截面3位于无叶扩压器的入口；无叶片扩压器出口和蜗壳入口的条件相同，因此，截面4位于无叶扩压器出口或蜗壳的入口；截面5位于蜗壳的出口。

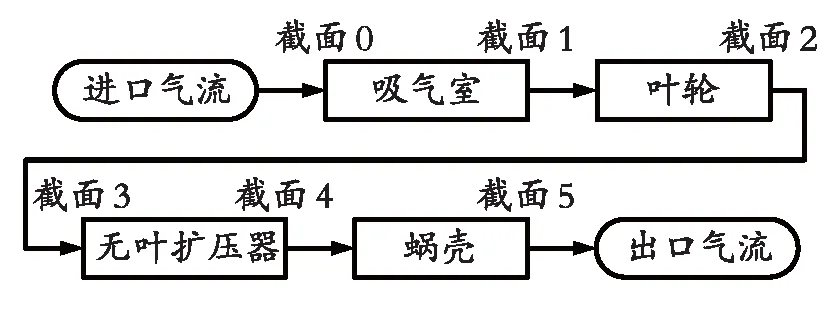
图2 特征截面划分示意图Fig. 2 Schematic diagram of feature section division

1.1 蜗壳损失模型的推导

为了收集扩压器后面或叶轮后面气体，并将其引导压缩机后面的输气管道或冷却器中，蜗壳是一个必要的元件。对蜗壳损失的计算，通常按式(1)计算[1]，如此计算得到的结果存在一个范围，偏差较大。将蜗壳损失进行划分，推导出各部分损失的计算公式：

(1)

其中，C4为无叶扩压器出口速度(m/s)；ζvol为蜗壳损失系数，取0.18～0.22。

对蜗壳内的流动做出假设：蜗壳内气流作一元不可压缩流动，忽略横截面上的二次流。将蜗壳损失划分为3个部分：径向冲击损失、周向冲击损失和壁面摩擦损失。

图3为蜗壳示意图，将蜗壳流道沿周向展开成如图4所示的扩压管道，沿扩压器出口有流体不断加入。

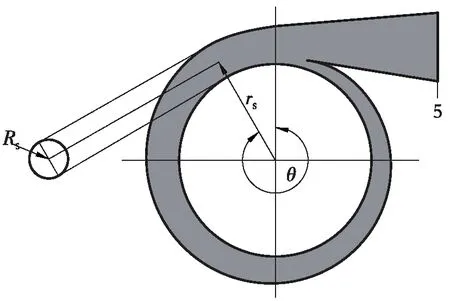
图3 蜗壳示意图Fig. 3 Schematic diagram of the volute

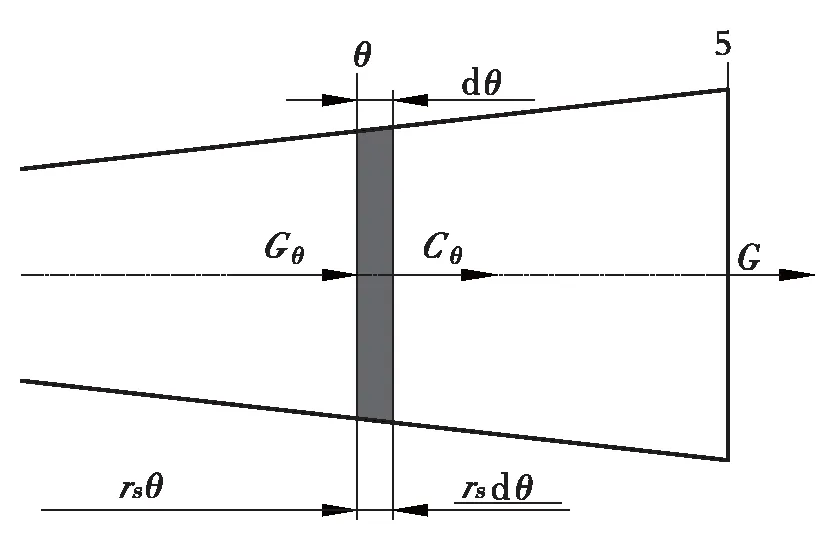
图4 蜗壳周向展开示意图Fig. 4 Schematic diagram of the circumferential expansion of the volute

1.1.1 径向冲击损失

因为在蜗壳流道内主要是周向运动，所以认为蜗壳入口绝对速度径向分量几乎全部损失，则径向冲击损失计算公式为

(2)

其中，Cr4为蜗壳进口气流速度径向分量(m/s)。

1.1.2 周向冲击损失

如果圆周方向无外力，则微元部分的周向速度应为

(3)

其中，Cu4为蜗壳进口气流速度周向分量(m/s)；r4为无叶扩压器出口半径(m)；rs为微元处至轴线半径(m)。但实际上其速度为

(4)

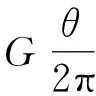
由于Cuθ≠Cθ，因此形成了损失，对微元部分来说，由于其质量流量占总质量流量的θ/2π，故微元部分的损失为

(5)

所以，整个蜗壳里的周向冲击损失：

(6)

1.1.3 壁面摩擦损失

将蜗壳沿周向展开，参照圆管沿程摩擦阻力计算方法计算蜗壳壁面摩擦损失。

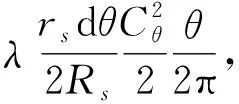
(7)

其中，沿程摩擦阻力系数：

(8)

其中，δ为表面粗糙度(mm)。

综上，蜗壳中的总损失为

Δhvol′=Δhr+Δhu+Δhf

(9)

1.2 理论功的计算

对于理论理论功的计算，叶轮出口速度分布修正系数及滑移系数有着重要作用。由于在叶轮出口处，气流速度的分布沿轴向和周向都是不均匀的，如采用通常的流量平均速度的径向分量来计算理论功，则所得之值将偏高很多，考虑到这种出口速度径向分量的不均匀性，应采用能量平均速度计算理论功，得到准确的数值，计算公式如下：

(10)

其中，Cr2为叶轮出口绝对速度的径向分量，单位m/s；ε2为速度分布不均匀修正系数。

如假设叶轮出口气流绝对速度的径向分量沿轴向及周向均作正弦变化，Wislicenus[17]得到ε2=(π2/8)2。三元叶轮出口速度分布比较均匀呈平坦形状，因此其ε2小于(π2/8)2，约为1.1～1.2。至于常规叶轮，出口速度分布不均匀性大，此值也就较大。根据相关离心压缩机实验结果得到ε2计算公式：

ε2=1.233 3-0.1φr2-10b2

(11)

其中，b2为叶轮出口宽度(m)；φr2为叶轮出口流量系数。

式(11)表明ε2与流量系数φr2及叶轮出口宽度b2有关，叶轮出口越宽，流量越大，则速度分布越均匀，而ε2也就越接近1。

由于叶片数量有限，叶轮出口相对气流角不同于叶片安装角，对于离心压缩机，可以使用滑移系数评估该偏差。Wiesner[18]、Qiu[19]等提出了滑移系数计算方法。由于一维初步设计中的叶片旋转参数未知，Qiu的模型不适用于预测初步设计中离心压缩机的性能。选用Wiesner经验公式：

(12)

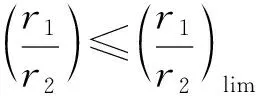
(13)

否则，

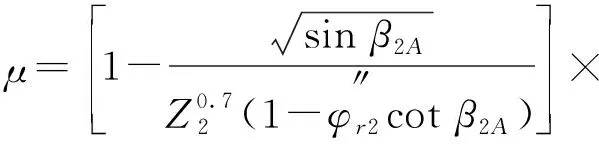
(14)

其中，能量平均流量系数为

(15)

其中，r1、r2分别为叶轮进、出口半径(m)；β2A为叶轮出口安装角(°)；Z2为叶轮出口叶片数。

叶轮理论功为

Δhth=U2Cu2-U1Cu1

(16)

其中，Cu1、Cu2分别为叶轮进、出口绝对速度周向分量，单位m/s；U1、U2分别为叶轮进、出口圆周速度(m/s)。

(17)

其中，U1、U2为叶轮进、出口圆周速度(m/s)；Cu1、Cu2为叶轮进、出口绝对速度周向分量(m/s)。

1.3 损失模型的选择

进气室损失模型参考文献[1]，叶轮损失和无叶扩压器损失模型依据文献[12]进行选用。其中，叶轮损失可分为叶片摩擦损失、冲角损失、叶片载荷损失、叶顶间隙损失、尾迹混流损失、轮阻摩擦损失、漏气损失和再循环损失。损失模型列于表1中。

1.4 整机性能预测

压缩机系统的整机效率和压比计算如下：

(18)

(19)

其中，η、τ分别为离心压缩机效率和压比；p00、p05分别为压缩机进、出口全压；叶轮内部损失为

Δhin=Δhinc+Δhsf+Δhbl+Δhcl+Δhmix

(20)

叶轮外部损失为

Δhpar=Δhdf+Δhre+Δhlk

(21)

2 实验对比

2.1 压缩机结构参数

研究对象为一台单级离心压缩机，其设计流量为1.33 kg/s,转速为12 000 rpm，压比为1.36。叶轮三维模型如图5所示，压缩机基本结构参数列于表2 和表3。

表1 选用损失模型汇总Table 1 Summary of selected loss models

图5 叶轮模型Fig. 5 Impeller model

2.2 压缩机试验台

按JB/T 3165-1999测试标准对离心压缩机进行测试。压缩机试验台为开式出气装置试验台，如图6所示，由实验管路、流量测量管路及节流装置等组成，进气口端面开向大气，而出气口端面与实验管路相连接。测量设备包括流量测量仪器、压力测量仪器、温度测量仪器、转速测量仪器及功率测量仪器，其测量精度分别为±0.5%、±0.5%、±0.5%、±0.2%和±1%。

表2 压缩机结构参数Table 2 Compressor structure parameters

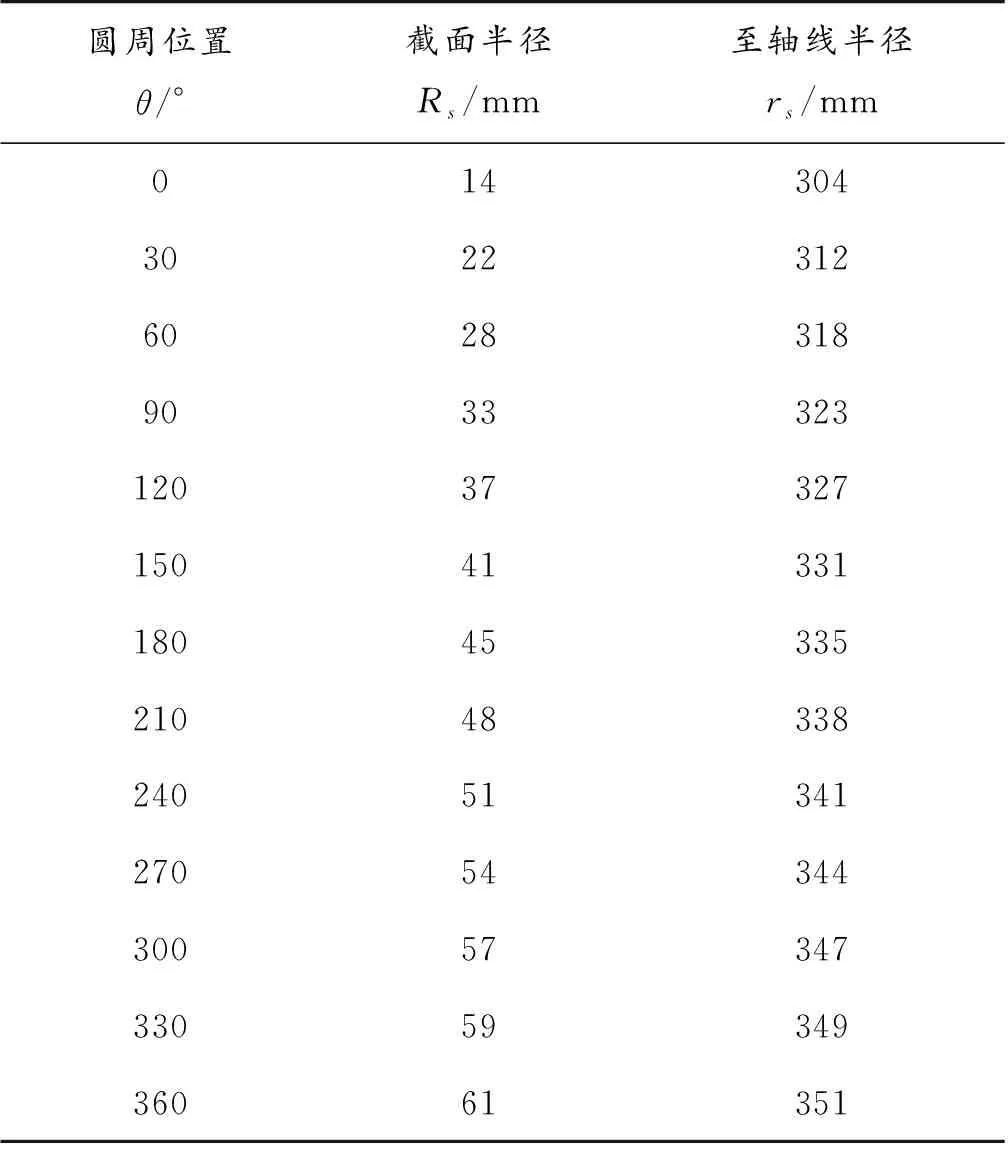
表3 蜗壳结构参数Table 3 Volute structure parameters

压缩机性能试验之前应将其调整到设计工况附近运行，经检查机械运转和全部仪表工作正常，且进出口气流温度、压力和管道壁面温度稳定后，再进行测量。测量时应从大流量到小流量测量，电动调节阀全开时为最大流量，测量到小流量范围时应对电动调节阀进行微调。当有振动和噪声突然变大的现象发生，表明当前工况处于喘振边缘。由于喘振流量点的流动极不稳定，给压缩机运行带来一定的危险性，在真正发生喘振的流量点进行测量是不允许的，故规定将最小流量工况视为喘振工况。

图6 离心压缩机实验台Fig. 6 Test rig of centrifugal compressor

2.3 预测结果与实验结果对比

预测结果偏差如表4所示，预测结果和实验结果对比如图7和图8所示。其中，A方法为修正理论功、采用新蜗壳损失模型；B方法为未修正理论功、采用新蜗壳损失模型；C方法为修正理论功、未采用新蜗壳损失模型；D方法为未修正理论功、未采用新蜗壳损失模型。

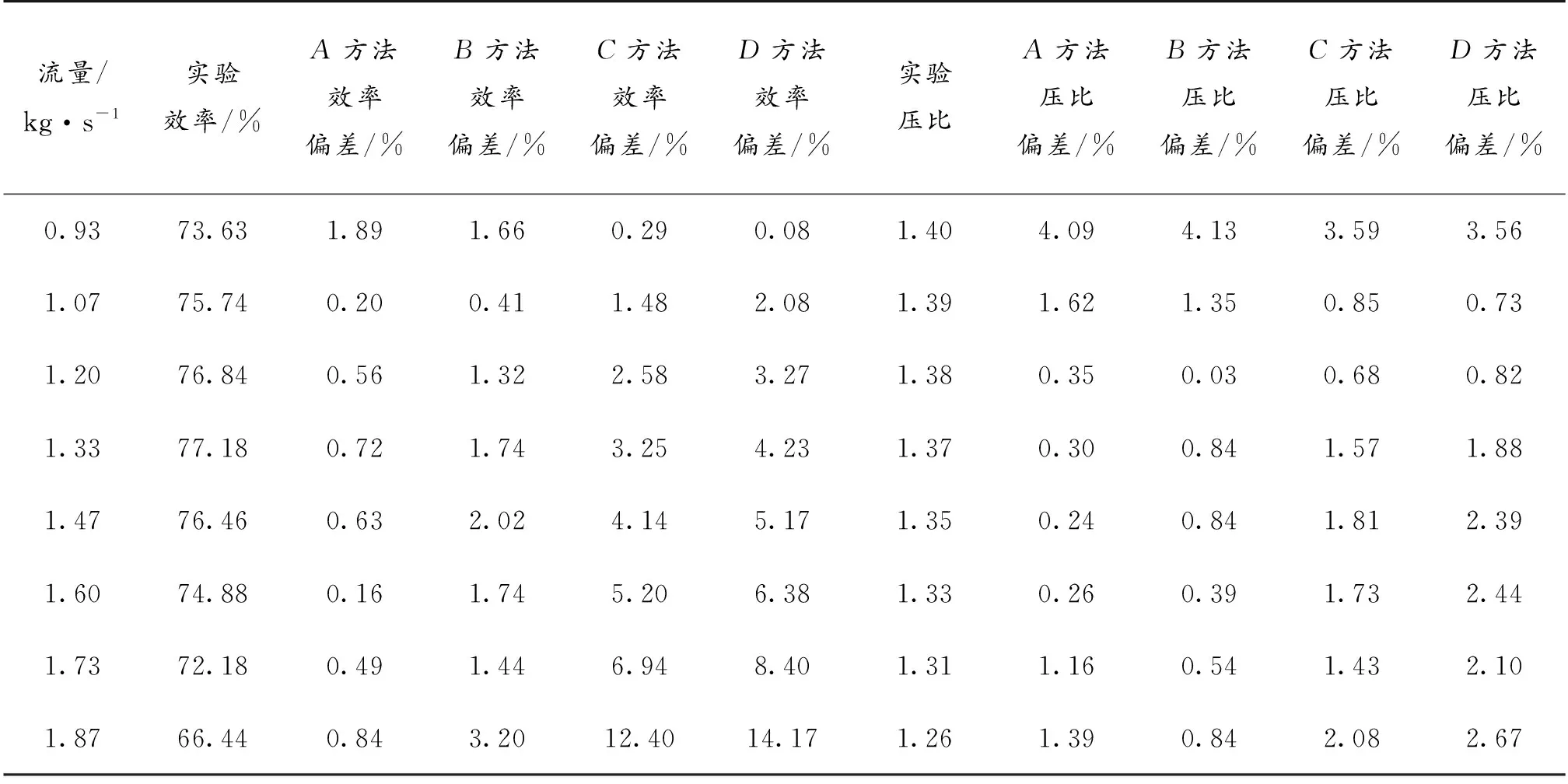
表4 预测结果偏差Table 4 Deviation of prediction results

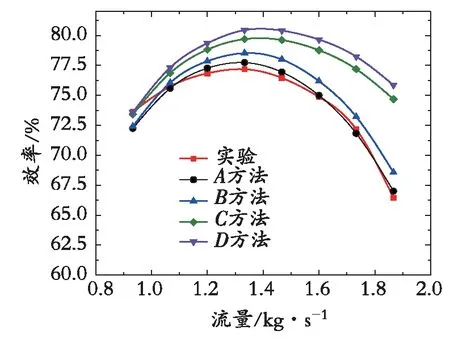
图7 效率曲线对比Fig. 7 Comparison of efficiency curve

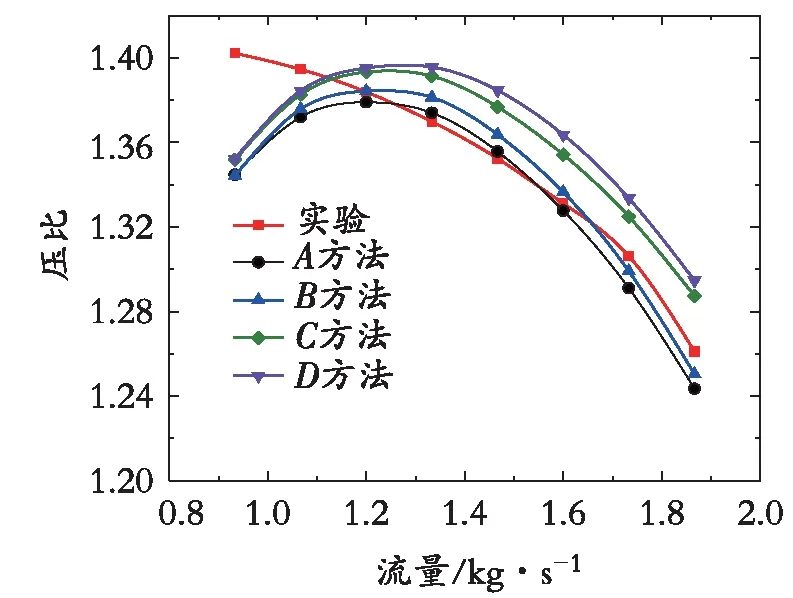
图8 压比曲线对比Fig. 8 Comparison of pressure ratio curve

由图7和图8可知，通过修正理论功或采用新的蜗壳损失模型均能减小预测偏差，其中采用新蜗壳损失模型效果更明显。同时修正理论功和采用新蜗壳损失模型预测效果最佳，效率预测偏差在设计点为0.72%，最大偏差小于2%；压比预测偏差在设计点为0.3%，最大偏差小于4%。

由图7和图8可知，远离设计工况时，预测偏差将增大，尤其是低流量区域，偏差将明显增大。损失模型是在某些离心压缩机实验数据的基础上总结、拟合得来，而在实际变工况中，流量的改变带来速度和冲角变化[1]，同时流场随之发生复杂变化，损失偏离了损失模型计算值；其次，计算损失时忽略了各种损失及各元件的相互影响，通过单独计算，叠加得到；而且有些损失模型在拟合时进行了假设，这些因素导致了偏差叠加和放大。

3 数值模拟分析

由于具有快速、准确、低成本的特点，数值模拟方法被广泛应用于叶轮机械的研究。利用ANSYS软件对压缩机经行数值模拟，对性能预测结果进行验证。

计算区域分为吸气室、叶轮、无叶扩压器和蜗壳，计算域进出口适当延长。网格采用ICEM-CFD软件生成，叶轮段生成六面体网格[20]，其余段生成四面体网格，并进行局部细化，如图9、图10所示。湍流模型选择SST模型，边界条件进口给定总压、总温，出口给定质量流量，所有固体壁面均设置为无滑移壁面[21]。数值模拟的结果和实验结果对比如图11所示，效率的变化趋势与实验结果吻合，最大偏差在4%以内。

图9 叶轮单流道网格Fig. 9 Impeller single channel grid

图10 压缩机整体网格Fig. 10 Compressor grid

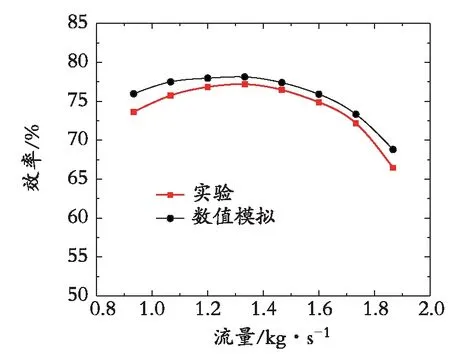
图11 数值模拟结果与实验结果对比Fig. 11 Comparison of the experiment result and the numerical result

3.1 蜗壳损失模型验证

将新蜗壳损失模型和传统损失模型预测结果与数值模拟结果对比，由图12所示。新蜗壳损失模型和传统损失模型的预测结果增减性均与数值模拟结果一致，即随着流量的增加，蜗壳损失随之增加。但是，传统蜗壳损失模型预测结果随着流量的增大逐渐偏离数值模拟结果，而新蜗壳损失模型预测结果的变化趋势始终与数值模拟结果相吻合，与离心压缩机在非设计工况下性能变化剧烈的情况相符。而且，新蜗壳损失模型预测结果偏差明显小于传统模型，能够更准确地预测蜗壳损失。

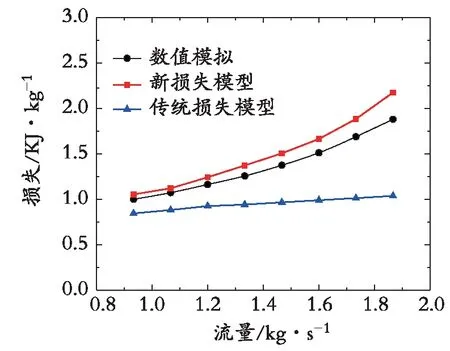
图12 蜗壳损失模型对比Fig. 12 Comparison of volute loss models

3.2 蜗壳损失分析

绘制蜗壳损失的各组成损失随着质量流量的变化趋势如图13所示，可得径向冲击损失和壁面摩擦损失都随着流量的增大而增大。而周向冲击损失随着流量的增大先减小后增大，在设计工况附近周向冲击损失最小。随着流量的增大，压缩机中气流主流速度增大，导致蜗壳径向冲击损失增大；主流速度增大，边界层中速度梯度增大，导致壁面摩擦损失随之增大。而随着流量的改变，离心压缩机的运行工况偏离设计工况，蜗壳内理论周向速度与实际周向速度差值变大，导致周向冲击损失随之增大。

蜗壳损失组成径向冲击损失、周向冲击损失和壁面摩擦损失在变工况下的占比如图14所示。由图14可知，随着工况的改变，径向速度损失占蜗壳总损失的15%～30%，周向冲击损失占21%～52%，壁摩擦损失占32%～48%。

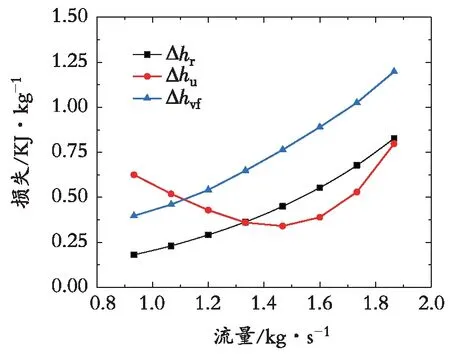
图13 蜗壳组成损失变化趋势Fig. 13 Variation trend of volute composition loss

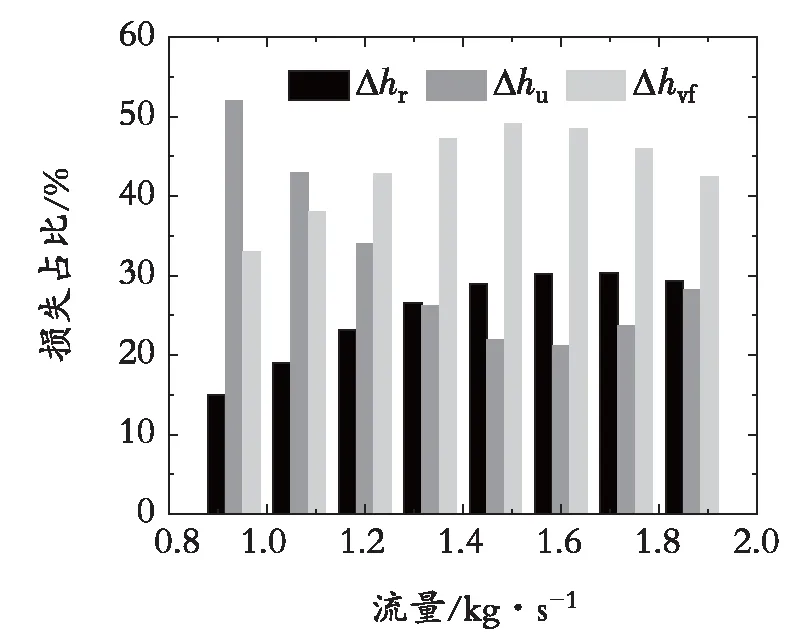
图14 蜗壳损失组成占比Fig. 14 Percentage of volute losses

变工况下，各组成元件损失在整个压缩机系统总损失中的占比如图15所示。由图15可知，随着工况的改变，进气室损失仅占压缩机总损失的1%，叶轮内部损失占25%～42%，叶轮外部损失占5%～11%，无叶扩压器损失占25%～50%，蜗壳损失占10%～26%。

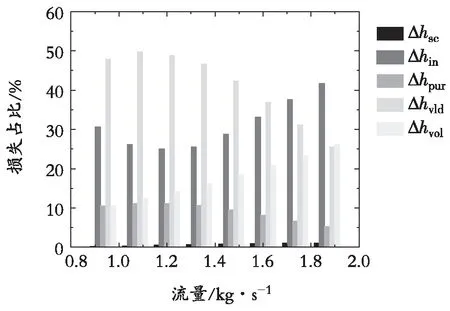
图15 离心压缩机损失占比Fig. 15 Percentage of centrifugal compressor losses

4 结束语

提出新的蜗壳损失计算模型，将蜗壳损失分为径向冲击损失、周向冲击损失和摩擦损失三部分进行计算，针对叶轮出口速度分布不均匀特性，利用能量平均的方法对叶轮出口速度和滑移系数进行修正，建立离心压缩机整机性能预测方法，通过与实验和数值模拟结果对比得到如下结论：预测方法能够准确预测单级离心压缩机整机性能，设计工况预测偏差在1%以内，变工况偏差在4%以内；提出的蜗壳损失模型能够更准确地预测蜗壳损失。蜗壳损失在压缩机总损失中占有不可忽视的比重，并且随着工况的变化而变化，采用合适的蜗壳损失模型能够减小离心压缩机性能预测结果的偏差。