空间薄膜结构刚柔耦合非线性动力学分析

邵琦，陆一凡，史创，岳洪浩，刘荣强

哈尔滨工业大学 机器人技术与系统国家重点实验室，哈尔滨 150001

1 引言

空间薄膜结构凭借大柔性、低刚度等特点成为极具前景的航天器结构，但同时也表现出极强的非线性，这使得结构动力学特性复杂且极易受到扰动。星体与附件的机动刚体运动是对空间薄膜结构产生扰动的主要因素之一，刚柔耦合效应下的结构动态响应将对空间薄膜天线等薄膜结构的正常工作产生极大影响。

目前大部分研究针对的是柔性杆、梁与薄板结构的刚柔耦合动力学问题。对于柔性梁结构，张广芸构造了包含非线性耦合关系的形函数，对降阶刚柔耦合连杆系统动力学方程进行运动与受力分析[1]；文献[2-4]建立了空间曲梁刚柔耦合有限元模型，考虑了“刚”与“柔”之间的相互影响；李铁寿对其柔性附件轻质梁耦合系统的五自由度动力学进行研究[5]。对于板结构，Yoo研究了在常规线性建模方法中忽略的运动诱导刚度变化项对板动力响应的影响[6]；沈超明针对中心刚体与柔性板系统，对比了零次近似模型与一次耦合模型的差异[7]；Yuan等人分析了太阳能板平移与转动的耦合效应[8]；陆栋宁等人对高分七号卫星板状天线的捕获运动对卫星姿态的影响进行研究[9]。

对于空间薄膜结构的刚柔耦合动力学，部分研究将薄膜结构简化等效为柔性梁或薄板结构，如：蒋建平将太阳翼等效为柔性梁，通过Lagrange方程建立了一次近似动力学模型[10]；而后，将其等效为薄板结构[11]，基于Kane方程建立一次近似动力学模型。其他研究则主要着眼于空间薄膜结构动态响应对卫星及其他附件的影响，如：Li基于虚功原理建立了太阳帆的刚柔耦合动力学模型，计算了不同机动过程下结构的动态响应情况[12]；Jin通过刚柔耦合模型分析了太阳帆振动对轨道、姿态及其控制力矩的影响[13]；Liu考虑薄膜帆的Von Karman非线性应变-位移关系，研究了其刚柔耦合响应对俯仰运动的影响[14]。

然而，少有文献针对完整的空间薄膜结构考虑其动态响应在刚柔耦合效应下的变化。由于天线的电气性能很大程度上依赖于薄膜反射面的面型精度，故面型响应精度对于空间薄膜天线结构而言十分重要。因此，分析刚体运动对空间薄膜结构的弹性动态响应的影响成为本文所关注的主要问题。

本文首先从理论模型的角度分析了几何非线性与刚柔耦合效应对结构动力学响应特性的作用，为后续薄膜结构面型动态控制奠定理论基础；而后，分析了刚体运动规律、结构基频与阻尼对大范围刚体运动下柔性结构的动态响应的影响，以指导卫星或附件调姿机动设计，可实现从扰动源头规避机动操作对空间薄膜结构动态响应激励。

2 空间薄膜天线刚柔耦合非线性动力学建模

由于空间薄膜天线型面精度要求较高，因此，以空间平面张拉薄膜天线为研究对象，针对由机动操作引起的动态响应进行研究。在轨卫星及其空间薄膜天线附件(展开后)如图1(a)所示。其中，薄膜花边的主要作用是使薄膜面内应力分布均匀，从而避免产生褶皱，而对结构的模态、基频等动力学特性影响较小[15]，但引入了复杂的边界条件。因此，本文采用如图1(b)所示的无花边张拉薄膜天线，在简化边界条件的同时，认为继承花边薄膜表面的平整性与应力分布的均匀性。本节将从空间薄膜天线几何非线性描述与刚柔耦合效应表达方面分别阐述。

图1 在轨卫星及其空间薄膜天线示意Fig.1 Schematic diagram of the in-orbit satellite with a membrane antenna

2.1 空间薄膜天线的几何非线性描述

本文应用有限元对空间薄膜结构大位移响应的几何非线性进行建模，认为柔性单元是经历大位移的构件，但单元内部的相对变形仍局限于小变形，即大位移、小变形问题。将框架、绳索和薄膜分别等效为空间梁单元、预紧的空间杆单元以及三角形薄膜单元，通过几何方程、物理方程以及单元势能来描述结构的几何非线性。

2.1.1 框架单元的非线性描述

框架每个节点具有三轴位移u,v,w以及三轴转动θx,θy,θz共6个空间自由度。其位移场δb可用单元形函数Nb与单元节点位移qb表达：

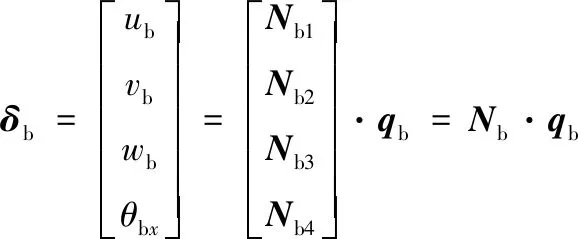
(1)

式中：ub,vb,wb分别为x,y,z三向的位移；θbx为绕x轴扭转的角度；下标b表示框架梁单元。考虑大位移和有限转动，将式(1)的位移场代入应变场与位移场的关系中，并用′与″分别表示变量对x的一阶导数与二阶导数，则框架梁单元应变场写为：

式中：

I4=[1 0 0 0]

考虑结构材料为线弹性与各向同性，根据广义Hooke定律，则梁单元的本构关系为：

式中：σb为单元应力场；Eb为材料的杨氏模量；Gb为材料的剪切模量。

空间薄膜结构在空间环境中不考虑重力，框架的单元势能即单元应变能，则单元势能可以表示为：

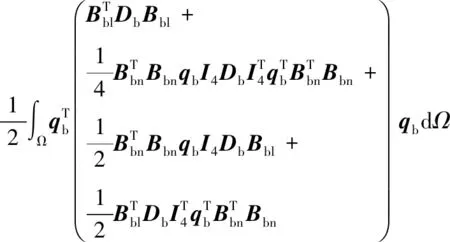
(2)

式中：Kbl与Kbn分别为梁单元刚度矩阵的线性部分与由考虑二阶效应产生的非线性部分，分别为：

2.1.2 绳索单元的非线性描述

张拉绳索每个节点具有u,v,w共三个空间自由度。其位移场δc可用单元形函数Nc与单元节点位移qc描述：

式中：uc,vc,wc分别为节点在x,y,z三向的位移；下标c表示绳索单元。由于绳索只有轴向伸长的变形，所以其应变场只考虑轴向应变。在大位移非线性情况下，绳索轴向应变与位移场的关系和框架梁单元相似，表示为：

式中：

考虑结构材料为线弹性与各向同性，根据广义Hooke定律，则绳索单元的本构关系为：

σcx=Ecεcs

式中：Ec为材料的杨氏模量。

由于绳索受到预张拉力，绳索的势能包括轴向伸长的应变能以及克服张紧力所做的功，则绳索的单元势能为：

对单元势能进行变分与时间上积分，则：

(3)

式中：Kcl与Kcn分别为绳索单元刚度矩阵的线性部分与由于二阶效应产生的非线性部分；Kc0为单元预张力等效刚度矩阵；QcΠ为单元预张力等效载荷列阵。四者分别为：

2.1.3 薄膜单元的非线性描述

张拉薄膜每个节点具有u,v,w共3个空间自由度，每个单元有3个节点。其位移场δm可用单元形函数Nm与单元节点位移qm描述：

式中：um,vm,wm分别为节点在x,y,z三向的位移；下标m表示薄膜单元。基于Kirchhoff薄板假设与Von Karman薄板大挠度非线性理论，将式(1)的位移场代入应变场与位移场的关系中，并用x′与y′分别表示变量对x与y的一阶导数，则薄膜单元各个方向应变与位移场的关系表示为：

εm=[εmxεmyγmxy]T=

式中：

薄膜结构属于平面应力问题，考虑结构材料为线弹性与各向同性，根据广义Hooke定律，则薄膜单元的本构关系为：

式中：Dm为薄膜的弹性矩阵；Em与μ分别为材料的杨氏模量与泊松比。

设薄膜单元的预张拉应力为：

σm0=[σmx0σmy0τmxy0]T

与绳索单元相似，薄膜的单元势能为：

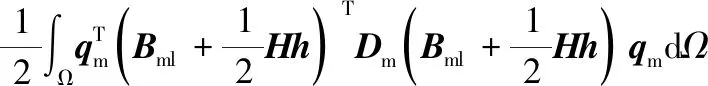
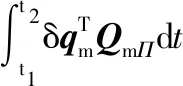
(4)

式中：Kml与Kmn分别为薄膜单元刚度矩阵的线性部分与考虑二阶效应产生的非线性部分；Km0为单元预张力等效刚度矩阵；QmΠ为单元预张力等效载荷列阵。四者分别为：

2.2 空间薄膜天线的刚柔耦合效应表达

空间薄膜天线在轨时姿态的调整以反射面与地面夹角的调整为主，即绕图1中x轴转动的刚体运动[16]。因此，本文考虑空间薄膜天线绕x轴转过一定角度的刚体运动。

柔性结构的典型特性之一即其结构的非线性，何泽青等人详细描述了考虑二阶非线性应变时结构的动力学特性[17]。对于大范围刚体运动引发的刚柔耦合效应，Kane指出，考虑二阶非线性变形位移场进行刚柔耦合分析时，可以捕捉到刚体运动对弹性运动动力学特性的耦合项[18]。本节将基于这一原理，对空间薄膜天线结构的刚柔耦合效应进行捕捉与描述。

图2 空间薄膜天线坐标系示意Fig.2 The coordinate systems of space membrane antenna

本节将先通过对结构动能的描述，建立刚体运动对结构弹性运动响应的耦合效应表达；然后基于哈密顿原理，建立空间薄膜天线的刚柔耦合非线性动力学模型。

2.2.1 单元的动能描述与刚柔耦合动力学方程表达

结构上任意一点p在全局坐标系下的位置矢量Rp表示为：

Rp=r0+A(rp+Nq)

式中：rp为p点在浮动坐标系下未发生弹性变形前的位置矢量；Nq为p点在浮动坐标系下的弹性变形。进而，p点在全局坐标系下的速度与加速度矢量分别为：

单元动能可表示为：

对单元动能进行变分，并在时间上进行积分，利用分部积分法，考虑等时变分在起始于终止时刻坐标的变分为零，可得：

(5)

式中：M为单元质量矩阵；G与KT为刚柔耦合引起的附加质量矩阵，分别表现为阻尼特性与刚度特性；QT为刚性运动加速度引起的外载荷。当不考虑刚柔耦合效应时，上式退化为仅包含质量矩阵M与惯性力矩阵QT的刚体动力学方程。以上各项具体分别表述为：

2.2.2 单元刚柔耦合非线性动力学方程及其组装

哈密顿原理通过寻找动势的时间积分的驻值来确定真实运动路线，表述为：

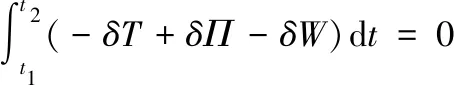
(6)

式中：T为动能；Π为势能；W为外力对系统所作的功。在2.1节中，空间薄膜天线的框架、绳索、薄膜三类结构各自的单元势能在时间上的积分已经得到，分别如式(2)、(3)、(4)所示；在2.2.1节中，结构各单元的动能在时间上的积分表达已由混合坐标法推出，如式(5)所示。将上述所得到的单元势能与单元动能均带入式(6)中，可得框架梁单元、绳索单元与薄膜单元的刚柔耦合动力学方程分别为：

(Kbl+Kbn+KbT)qb+QbT=Fb

(7)

(Kcl+Kc0+Kcn+KcT)qc+QcΠ+QcT=Fc

(8)

(Kml+Km0+Kmn+KmT)qm+QmΠ+QmT=Fm

(9)

式中：Mb、Mc、Mm分别为三种单元的质量矩阵；Fb、Fc、Fm分别为三种单元所受的外载荷列阵；Cb、Cc、Cm分别为三种单元的阻尼矩阵；Kbl、Kcl、Kml分别为三种单元的线性刚度矩阵；Kbn、Kcn、Kmn分别为三种单元的非线性刚度矩阵；下标0、Π、T分别表示由于预紧力、应变能、刚柔耦合效应产生的动力学成分，如Kc0、Km0分别为绳索单元与薄膜单元由于预紧力产生的刚度矩阵，QcΠ、QmΠ分别表示绳索单元与薄膜单元由于预应变产生的载荷列阵，KbT、KcT、KmT分别为三种单元由刚柔耦合效应引起的动刚度矩阵。将空间薄膜天线所有单元的各个矩阵按节点及其自由度的关系对应组装，可以得到形如式(7)～(9)的空间薄膜天线刚柔耦合非线性动力学模型，即：

(Kl+K0+Kn+KT)q+QΠ+QT=F

本章从理论上描述了几何非线性与刚柔耦合效应对结构动力学带来的影响，相比于商业软件黑匣子式的操作与数值结果，理论模型的表达有助于理解并提炼空间薄膜结构系统最本质的非线性与耦合动力学行为，以更全面地指导结构的动力学设计优化以及结构响应控制研究。

3 刚柔耦合非线性响应的预测与验证

上一节中所得到的空间薄膜天线动力学模型为二阶变系数微分方程组，是一种强耦合、时变、强非线性的方程组，本文将利用Wilson-θ法进行计算与求解，从而实现对空间薄膜天线结构刚柔耦合动态响应的预测。考虑空间薄膜天线的刚体运动自某一转速减速至停止，对结构在停止过程中及停止后的动态响应问题进行研究。选取薄膜工作区域内A点作为响应分析参考点，通过与文献[16]的结果进行对比，以验证本文建模方法的正确性。本节所研究的空间薄膜天线如图1 (b)所示，四周边框固定，材料与几何参数如表1所示[16]。

表1 空间薄膜天线材料与几何参数Table 1 Material properties and geometry parameters of the membrane antenna model

空间薄膜天线某些模态的频率如表2所示。本算例中，考虑空间薄膜天线初始转速为36°/s，分别计算经过0.000 1s和1 s将速度减至0时的结构动态响应。前一种情况接近瞬时停止，与文献[16]相对应。考虑结构受比例阻尼C=αM+βK，其中α与β均为0.001。取薄膜面上坐标(-0.703 6,0.426 7)为A点，其面外位移响应曲线如图3所示，其中，实线与虚线分别对应瞬时与1 s停止的情况，前者与文献[16]相应结果的对比如表3所示。

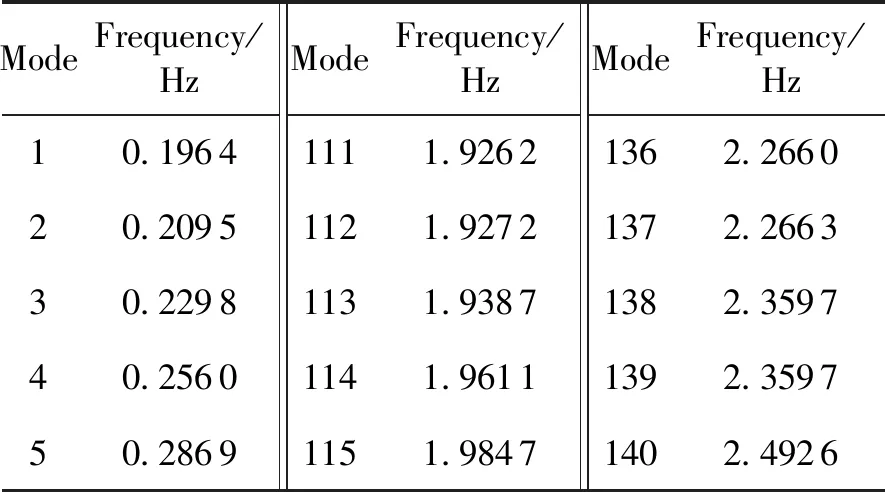
表2 空间薄膜天线算例模态频率Table 2 Natural frequencies of the membrane antenna

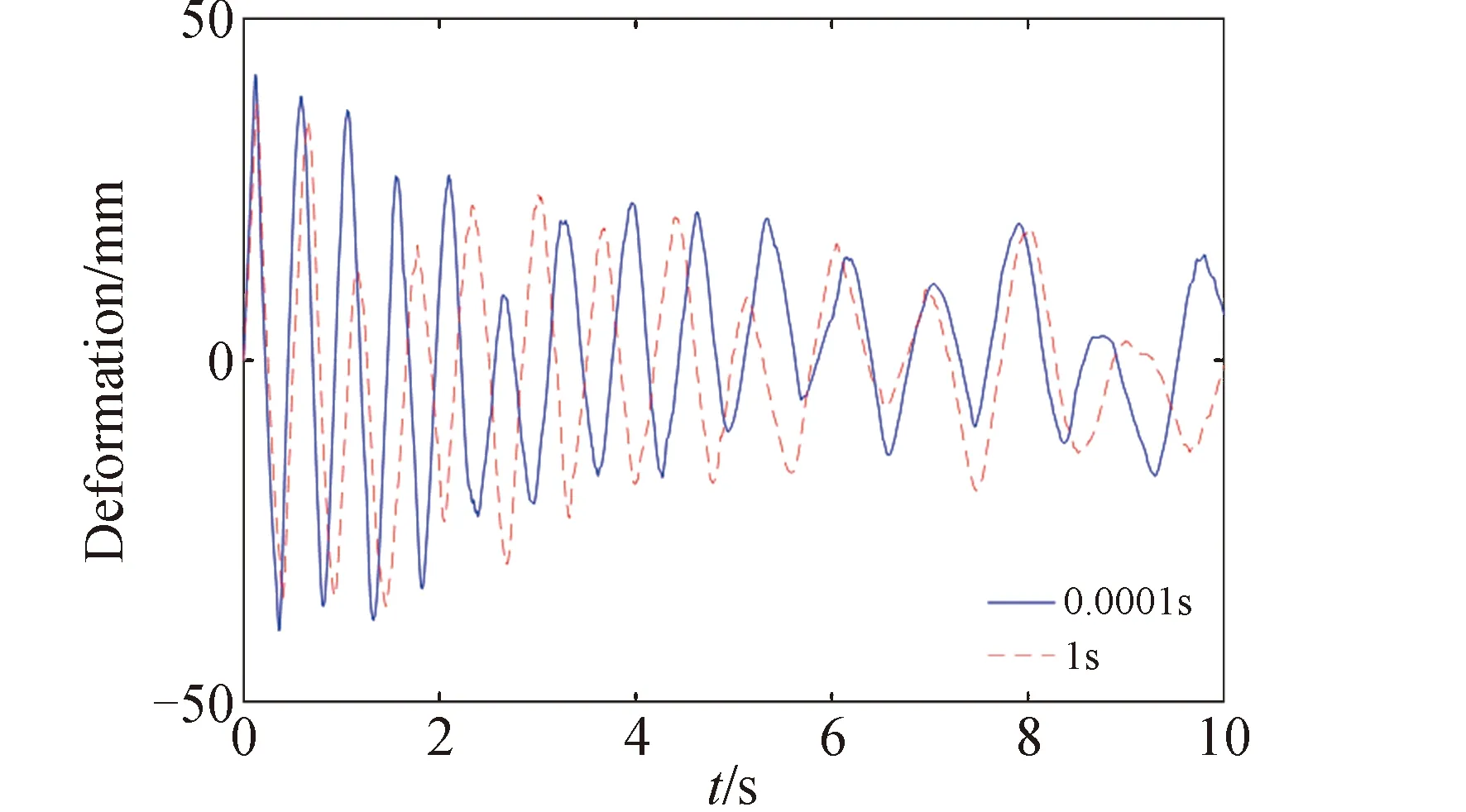
图3 A点的位移响应曲线Fig.3 The deformation response of A

表3 位移响应动力学特性比较Table 3 Dynamic characteristics compared with literature

本文模型响应频率与文献[16]相比，前10 s内相差较大，而前2 s内偏差较小，这是由于本文设置的阻尼使振幅衰减，进而非线性响应频率减小。因此，本文计算的响应结果在一定程度与文献结果相一致，可以验证所建立的刚柔耦合非线性动力学模型正确性。

4 刚体运动对动态响应的影响与分析

上一节中，A点相应频率并不表现为结构基频，且在两种情况下的响应频率有明显不同，瞬时停止的响应更快。因此，结构刚柔耦合响应频率与刚体运动规律有关。本节将针对空间薄膜天线在不同刚体运动规律下的响应进行分析。空间薄膜天线模型如图1(b)所示，各项材料与几何参数如表4所示，框架未注明参数与上一节相同。

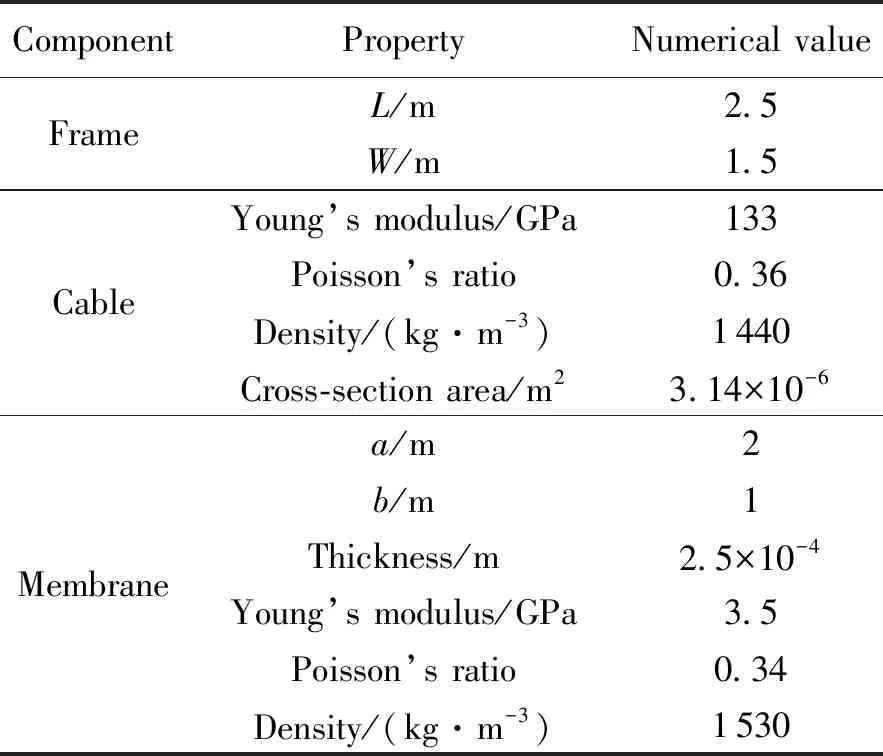
表4 绳索、框架与薄膜的各项参数Table 4 Properties of cable，frame and membrane

本节中，通过调整绳索张拉力得到不同基频的模型1、模型2、模型3，讨论初始转速、减速历时及对应加速度对三种结构响应的影响，并对其响应结果进行时域与频域的分析，各算例涉及的模型相关参数及其运动规律分别如表5与表6所示。绳索张紧力与薄膜结构频率关系并非本文重点关注的内容，相关分析可参考文献[19]。为简化表达，以下表述中“模型1/2/3”均表述为“M1/M2/M3”。

表5 算例模型相关参数Table 5 Properties of different models

表6 刚体运动规律Table 6 Rigid motion laws in different cases

首先，讨论模型从一定初始转速经历不同时长至停止时的动态响应情况。M1从π/5 rad/s分别经历0.1 s、1 s、2 s停止，A的面外变形响应曲线如图4所示，其时域与频域分析如表7所示。可以看出，动态响应的频率与振幅均会随着停止历时的增长而降低。这表明结构响应频率会随着历时的增加而减小。

图4 M1中A点在不同历时情况下的z向变形响应曲线Fig.4 Deformation responses in z direction of A in model 1 with different durations

表7 M1中A点在不同历时情况下动态响应特性Table 7 Dynamic characteristics of A in model 1 with different durations

其次，分析了模型自不同初始转速经历相同时间停止时的动态响应情况。M1分别以π/2、π/5、π/100的初始角速度，经过0.1 s后停止刚体转动，三种情况下A点的面外变形与动态响应特性分别如图5、表8所示。显然，动态响应的频率随着初始速度的减小而降低；最大变形峰值受初始转速影响很大，初始转速降低时最大变形峰值也显著减小。上述结果表明：动态响应的频率受刚体运动加速度影响，即对于同一结构，加速度越大，激励的响应频率越高；而振动的能量取决于初始动能的大小，即变形峰值与转速正相关。

图5 M1中A点在不同初始转速下的z向变形响应曲线Fig.5 Deformation responses in z direction of A in model 1 with different initial velocities

表8 M1中A点在不同初始转速下动态响应特性Table 8 Dynamic characteristics of A in model 1 with different initial velocities

最后，分析了不同模型在相同刚体运动规律作用时的动态响应情况。M1、M2、M3初始转速均为π/100 (rad·s-1)，经过0.1 s速度减为0，三种模型中A点的z向变形时域曲线和动态响应特性分别如图6与表9所示。可以看出，在相同运动规律下，动态响应的特性主要取决结构的动力学特性：变形响应频率与结构基频正相关，而最大变形峰值与结构基频负相关。

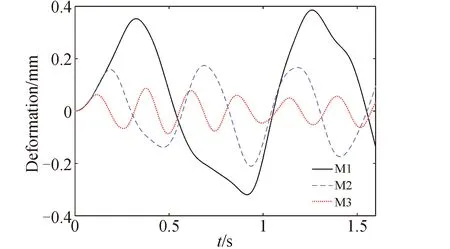
图6 不同模型A点在同种运动规律下的z向变形响应曲线Fig.6 Deformation responses in z direction of A in different models

表9 M1、M2、M3中A点在同种运动规律下动态响应特性Table 9 Dynamic characteristics of A in different models

综上所述，刚体运动加速度可以等效为一种谐激励，可以激起结构特定范围频率的响应；而结构的动能则对应输入动力学系统的能量，决定了结构所能达到的最大变形。因此，为防止机动操纵激起结构的剧烈振动，需要结合结构动力学特性合理设计刚体运动规律。

5 结论

考虑结构的几何非线性与大范围运动时的刚柔耦合效应，建立了空间薄膜天线刚柔耦合非线性动力学有限元模型，并基于数值计算讨论分析了刚体运动规律与结构动力学特性对薄膜弹性动态响应的影响，结论如下：

1)所建立的动力学模型极大程度地保留了平面薄膜天线的结构组成及其动力学特性，从理论角度分析了非线性与刚柔耦合效应对结构动力学特性影响；

2)由空间薄膜结构动态响应数值分析可知，刚体运动规律对空间薄膜结构的动态响应特性有显著影响，且其效应还与结构基频和阻尼有关；

3)空间薄膜结构刚柔耦合动态响应的频率随着刚体运动的初速度与加速度以及结构基频的增大而增大，但在阻尼作用下衰减加快；

4)空间薄膜结构刚柔耦合动态响应的变形幅值随着刚体运动的初速度与加速度的增大而增大，但随着结构基频与阻尼的增大而减小。

本文所建立模型可为空间薄膜结构的面型预测与控制提供理论基础，而刚体运动与动态响应特性间的规律将为特定结构的机动操纵设计提供指导。