基于响应面法的饲喂机器人螺旋输送轴结构优化*

□ 强 铎 □ 李海军 □ 尤福顺 □ 李 峤 □ 郝文博

内蒙古农业大学 机电工程学院 呼和浩特 010018

1 优化背景

内蒙古自治区地缘辽阔,草资源丰富,适合牛羊生存。随着我国科技的快速发展,当地大多数羊只饲养厂已经引进各式各样的饲喂机器代替人工饲喂,这直接带动了我国饲喂机器的发展[1]。考虑到经济效益,对于中小型饲养厂而言,价格实惠、操作简单的小型可移动式羊只饲喂类机器更适宜应用,但是这类设备大多存在易故障、饲料输送慢等问题[2]。为了满足内蒙古地区中小型羊只饲养厂的需求,提高饲喂工作效率,增加收益,笔者以羊只饲喂机器人为研究对象,采用响应面法对其螺旋输送轴进行结构优化,从而提高饲料输送的效率。

2 羊只饲喂机器人简介

羊只饲喂机器人主要用于饲喂羊只,可将存于料仓中的饲料通过螺旋输送机构输送至动物的料槽中,输送的饲料为玉米类颗粒饲料。羊只饲喂机器人内部结构如图1所示。

▲图1 羊只饲喂机器人内部结构

羊只饲喂机器人的料仓起存料下料作用,底部长800 mm,宽130 mm,侧壁倾角为45°,整体由2 mm厚的Q235钢板焊接而成,载质量为230.85 kg。饲料通过料仓最底部的条形广口排料口进入螺旋输送机构的U形槽。

螺旋输送机构是羊只饲喂机器人完成下料作业的主要机构。螺旋输送轴作为螺旋输送机构的主要构件,一般由螺旋叶片与转轴焊接而成。笔者研究所用的螺旋叶片为满面式正螺旋面叶片,直径为130 mm,厚为3 mm,螺距为150 mm,由3 mm厚的Q235钢制成。转轴选用轴类常用材料Q235钢,直径为60 mm。螺旋输送轴长度为1 200 mm,水平放置,采用右螺旋单口进料单口出料形式,输送量为5.76 t/h。螺旋输送轴质量为29.72 kg,体积为3 786 cm3,U形槽与车架通过螺栓连接。

螺旋输送轴实物如图2所示。

▲图2 螺旋输送轴实物

3 螺旋输送轴受力分析

螺旋输送轴受力分析如图3所示。转轴左端为全约束支撑,受到轴向力Fa和法向力FN共同作用。转轴右端可绕轴心自由旋转,约束位置位于轴承圆柱支撑表面,只受到法向力FN的作用。在饲料输送过程中,运动状态的饲料沿轴向和周向做复合运动[3],因此饲料对螺旋输送轴有一定的作用力。对螺旋叶片上的任意一点进行受力分析,物料在输送时会对叶片产生挤压力F。F与叶面垂直,运用空间正交分解法将F分解为平行于转轴的轴向力FZ、垂直于转轴的法向力FN,以及切向力FT。

▲图3 螺旋输送轴受力分析

在饲料运输过程中,轴向力FZ作用于螺旋叶片,对转轴的影响较小[4],所以直接采用安全余量内的尺寸进行设计计算。在转轴转动时,饲料挤压产生的切向力FT与电机作用于转轴的扭矩M达到平衡。对于法向力FN,饲料在运输过程中的不均匀性及饲料堆积对螺旋输送轴产生方向向下的压力,这两个力共同作用于螺旋输送轴。

4 螺旋输送轴三维建模

依据螺旋输送轴原始尺寸,应用SolidWorks软件建立螺旋输送轴的三维模型,如图4所示。

▲图4 螺旋输送轴三维模型

5 响应面法应用

5.1 优化变量确定

在确定优化的设计变量时,一般根据研究对象的形状尺寸和特征进行选择[5]。

笔者的优化目标是减小螺旋输送轴的体积和质量。对于螺旋输送轴而言,转轴的各项尺寸参数影响最大,综合考虑之后,选择转轴直径、螺距、叶片厚度作为优化的设计变量,优化范围取各变量的±10%,详细取值见表1。选择螺旋输送轴的体积、质量作为优化目标函数。

表1 设计变量取值

5.2 响应面模型构建

在选取所需样本点时,需要使用最少且最全面的样本点对设计空间进行填充,选取的点需要尽量满足均匀性和对称性要求。采用试验设计方法选择拟合响应面[6]试验的样本点,采用ANSYS DX软件中的OSF(Optimal Space-Filling)样本填充法自动生成所需的样本点,再对各项变量的不同数值进行不重复组合,具体见表2。

对螺旋输送轴结构优化最终是为了提高羊只饲喂机器人的下料速度,因此减小螺旋输送轴体积,增大单位时间内的输送量是主要手段。笔者在保证正常输送物料的条件下,决定将螺旋输送轴的体积作为第一优先级,其次是转轴质量。

应用OSF生成试验所需的样本点,建立响应面模型,如图5所示。

表2 样本点

▲图5 响应面模型

由响应面可以看出,随着螺距的减小和转轴直径的增大,螺旋输送轴的体积增大。

5.3 模型拟合精度验证

建立响应面模型之后,需要验证其拟合精度,以确定是否可以预测各个设计变量的响应值。响应面模型拟合数值界面如图6所示。由图6可知,目标函数的测定因数为1,均方根误差、相对最大绝对误差、相对平均绝对误差三项均接近于零,由此可以证明响应面模型的拟合精度相对较高,能够预测各设计变量的响应值[7]。

▲图6 响应面模型拟合数值界面

6 优化计算

6.1 多目标遗传算法

计算响应面模型的算法采用可以解决多个数值目标达到全局最优化的问题的多目标遗传算法[8-9]。在进行计算时,优化模块系统中默认从响应面模型中先取100个设计点进行计算。如果在这些点内出现最优解,系统会自动显示结果并结束计算。如果没有出现最优解,系统会在之前计算的基础上再增加100个点接着计算,依次类推,直到出现最优解时系统自动停止计算。转轴直径、螺距、叶片厚度三个设计变量在计算中的数值变化情况如图7所示。由图7可以看到,随着计算点数的增多,三个设计变量的数值在各自的取值范围内改变。

目标函数螺旋输送轴体积、质量随计算点数增多的变化情况如图8所示。

多目标遗传算法最终迭代结果如图9所示。图9中五条竖线从左至右依次表示转轴直径、螺距、叶片厚度、螺旋输送轴体积、螺旋输送轴质量,竖线两端点处数值为设计变量的取值范围,折线最终趋近于横轴,表示算法结果已经收敛,在这一情况下再继续迭代,之后的数值也不会有明显的变化,说明得到最优值。图9中折线与竖线的交点为设计变量的遗传算法优化计算结果,交点处的坐标为设计变量在取值范围内的最优数值。

▲图7 设计变量变化情况

6.2 帕累托解

螺旋输送轴的设计变量有三个,目标函数有两个,为防止出现在计算其中一个设计变量达到最优时导致其余设计变量不能达到最优的情况,选择帕累托解进行最后的优化计算,找出螺旋输送轴目标函数最优解的集合,即帕累托最优解集[10]。多目标函数的帕累托最优解集在空间上会形成帕累托解前沿面[11-12],螺旋输送轴的各个设计变量经过优化计算后的帕累托解前沿面如图10所示。最终生成的样本点曲线如图11所示。

▲图8 目标函数变化情况▲图9 多目标遗传算法迭代结果

6.3 优化结果分析

采用多目标优化计算方法,在一定的约束条件下得到转轴直径为50.06 mm,螺距为140.35 mm,叶片厚度为2.7 mm。对优化后的参数取整,转轴直径为50 mm,螺距为140 mm,叶片厚度为2.7 mm。优化前后设计变量对比见表3。

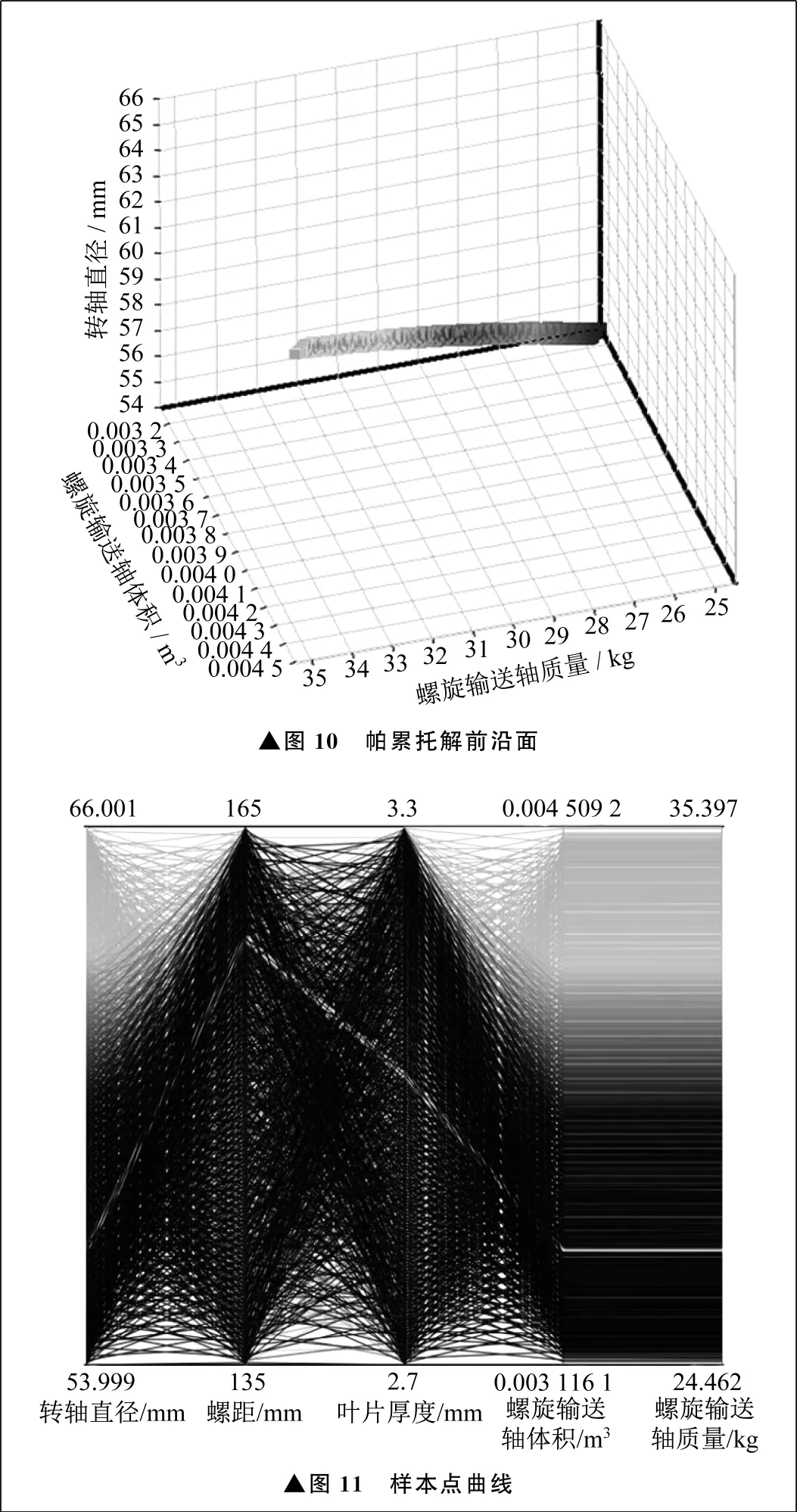
▲图10 帕累托解前沿面▲图11 样本点曲线

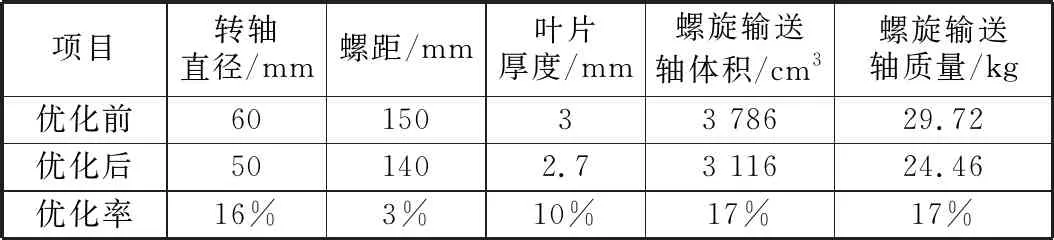
表3 设计变量对比

由表3可以明显看出,各个设计变量与优化前比较都有所减小,螺旋输送轴体积的减小使羊只饲喂机器人螺旋输送机构的输送空间增大了670 cm3。

对优化后的螺旋输送轴进行加工制造,并将羊只饲喂机器人组装完成,进行饲料输送,结果证明优化后饲料输送的效率明显提高,达到了预期目标。

7 结束语

笔者通过响应面法和多目标遗传算法对羊只饲喂机器人螺旋输送轴进行优化设计,最终减小了螺旋输送轴的体积和质量,使羊只饲喂机器人螺旋输送机构的输送空间增大了670 cm3,增大了螺旋输送轴在单位时间内的输送量,提高了羊只饲喂机器人的饲料输送效率。羊只饲喂机器人适用于内蒙古地区中小型羊只饲喂厂,效率提高可以使饲喂羊只的工作更加高效、准时,节省大量时间,进而提高羊只饲喂厂的经济效益。