膨胀土边坡的水平膨胀力及桩板结构内力分析
2022-02-23林宇亮张震罗桂军肖洪波杨果林鲁立段君义
林宇亮,张震,罗桂军,肖洪波,杨果林,鲁立,段君义
(1.中南大学土木工程学院,湖南长沙,410075;2.中南大学轨道交通工程结构防灾减灾湖南省重点实验室,湖南长沙,410075;3.中建五局土木工程有限公司,湖南长沙,410004)
膨胀土是一种工程性质复杂的黏性土体,具有遇水膨胀、失水收缩的特点[1]。膨胀土的特殊性质导致对膨胀土边坡的治理难度非常大。目前,对膨胀土边坡治理的主要理念为“刚柔相济、以柔治胀、防渗保湿”。其中,桩板结构可结合墙后砂垫层或减胀层,达到“刚柔相济”的目的,在膨胀土边坡支挡工程中得到了广泛应用。对于膨胀土边坡桩板结构,在设计过程中除了应考虑土压力作用外,还应考虑由于膨胀土自身性质而产生的膨胀力对桩板结构服役稳定性的影响。对于膨胀土而言,当土体含水率不发生变化时,其力学性质与常规土体的力学性质几乎没有差异。但在自然状态下,当环境水分侵入土体后,膨胀土会产生膨胀效应,因桩板结构的约束作用,会在墙后产生水平膨胀力,从而影响桩板结构的稳定性和服役性能。因此,在桩板结构设计过程中,需要明确水平膨胀力的大小和分布特点,从而指导膨胀土地区桩板墙结构的合理设计。关于膨胀土边坡桩板结构的分析和计算,国内外学者主要集中于水平膨胀力的大小和分布规律方面。汪鹏福[2]以膨胀土路堑边坡桩板墙结构为研究对象,基于现场实测数据研究了桩、板后土压力分布与土壤湿度变化规律,并分析了水平膨胀力沿深度的分布情况。张颖钧[3]通过对不同地区膨胀土进行水平膨胀力测试,给出了不同地区水平膨胀力的分布形式,并据此对膨胀土地区挡土墙结构进行了设计计算。RICHARDS[4]以澳大利亚阿德莱德混凝土挡土墙为研究对象,通过长周期观测,获得了自然条件下膨胀土水平膨胀力的分布形式。MOHAMED 等[5]基于现场实测方法,对侧向约束条件下水平膨胀力的分布形式进行了研究,得到了给定密度和含水率条件下水平膨胀力的分布结果。KHATTAB 等[6]通过室内试验,测试了侧向约束条件下水平膨胀力的分布形式,设计了试验装置使土体充分膨胀,并对水平膨胀力分布规律进行了长期监测。KASSIFF等[7]开展现场试验和室内试验分析了膨胀土的水平膨胀力,探究了理论假设条件下的结果与实际观测结果之间的相关关系,研究结果表明两者具有良好的相关性,有助于对水平膨胀力的预测。杨果林等[8]采用室内试验与现场试验相结合的方式,研究了水分浸入膨胀土时桩板墙的水平膨胀力分布形式,认为水平膨胀力沿深度方向呈梯形分布规律。ZHANG 等[9-10]通过改进的膨胀力测量装置,测试了侧向约束条件下水平膨胀力的分布形式,讨论了含水率、干密度和浸没竖向压力等因素对水平膨胀力分布形式的影响,并选取实际工程案例进行了验证。LLU等[11]建立了竖向膨胀力与水平膨胀力之间的计算关系式,并将这个关系式应用到挡土墙结构的水平土压力计算中,最后开展大型离心机试验,验证了所提出计算方法的可行性。于琳茗[12]通过现场实测和室内离心试验,对基坑工程中膨胀土水平膨胀力分布形式进行了测试,结果表明基坑侧壁水平膨胀力沿深度方向先增加后减小。已有研究成果促进了人们对膨胀土水平膨胀力分布形式的认识,但既有研究成果存在一定的差异性,尚未形成统一的膨胀土水平膨胀力分布结果,也没有考虑膨胀力影响的桩板结构标准化设计。为此,本文以膨胀土边坡桩板结构为研究对象,结合既有研究成果和室内模型试验,探讨水平膨胀力的计算方法,基于水平膨胀力分布形式推导桩板结构的桩身内力计算公式,并结合现场监测结果进行对比验证。
1 水平膨胀力计算公式的推演
1.1 膨胀土中含水率变化规律
自然状态下土体含水率分布是影响膨胀力分布形式的重要因素,其中,含水率变化是诱发膨胀力大小和分布发生变化的主要原因。在工程实践中,膨胀土地区的支挡结构损坏主要是膨胀土中含水率变化而诱发的膨胀力所致,因此,有必要分析膨胀土含水率的变化规律。对膨胀土含水率进行现场监测发现,旱季时,自然状态下土体含水率沿着深度方向逐渐增大,并趋于一个定值,而在雨季时,土体在一定深度内趋于饱和,含水率则沿深度相对保持稳定,如图1所示。对土体含水率进行处理,将雨季与旱季的土体含水率相减,作为季节交替时土体内部含水率的变化,如图2所示。为获得土体含水率变化量沿深度变化规律的定量结果,对图2所示结果进行拟合分析,拟合结果表明,土体含水率变化量沿深度呈负指数分布,其数学表达式为
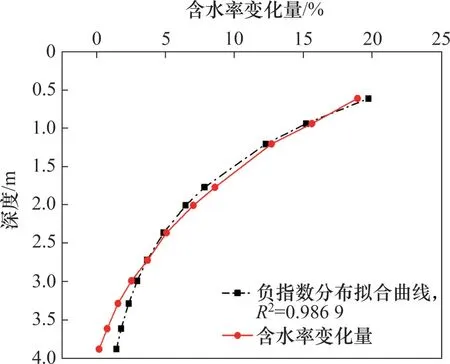
图2 含水率变化量沿深度分布情况Fig.2 Distribution of water content variation along depth

式中:Δw为不同深度处的含水率变化量;Δwmax为含水率变化量最大值;b为含水率变化量分布系数(b<0),需结合现场测试和分析确定;z为深度。
1.2 膨胀土的竖向膨胀力
膨胀土的竖向膨胀力直接影响着水平膨胀力的发挥。在自然状态下,膨胀土的含水率变化量沿深度方向的分布可按负指数分布考虑。含水率变化对竖向膨胀力的影响显著,需通过试验进一步分析竖向膨胀力与含水率变化量之间的相关关系。在试验过程中,保持土样干密度不变,通过改变初始含水率来分析含水率变化量与竖向膨胀力之间的关系[13]。试验均在WG-5轻便固结仪中进行,采用平衡法测量竖向膨胀力,可得到含水率变化量与竖向膨胀力之间的关系,如图3所示。由于试验中限制了膨胀土的水平和垂直向变形,给出结果的竖向膨胀力可认为是无膨胀变形的竖向膨胀力Pv。不同初始含水率土样的竖向膨胀力Pv与含水率变化量Δw大致呈线性关系,即
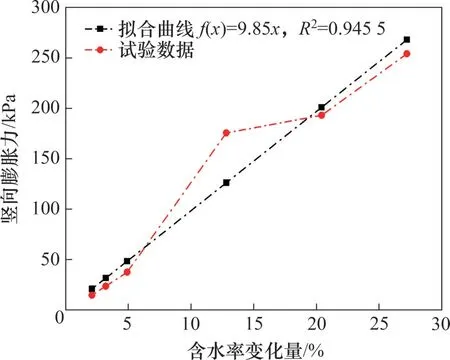
图3 竖向膨胀力与含水率变化量的关系曲线Fig.3 Relation curves of vertical swelling pressure and water content increment

其中:Pv为只考虑含水率影响的竖向膨胀力;A为竖向膨胀力与含水率变化量关系曲线的斜率;Δw为含水率变化量。
联立式(1)和式(2),土体的竖向膨胀力Pv可表示为
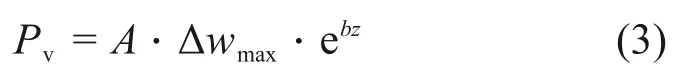
由式(3)可知,当深度z=0时,Pv取最大值,即Pvmax=A·Δwmax,此时,Pvmax可理解为膨胀土在约束条件下因含水率变化而引起的最大竖向膨胀力。
上述结果仅考虑了含水率变化量对竖向膨胀力的影响。对于自然状态下的膨胀土,除了应考虑土体含水率变化外,还需考虑上覆荷载作用时膨胀土可能产生的竖向变形以及由此对竖向膨胀力的影响。当不考虑附加荷载时,在自然状态下,不同深度的膨胀土承受不同的上覆荷载,从而影响竖向膨胀力的产生。为了明确自然状态下膨胀土竖向膨胀力的分布特点,应分析竖向膨胀力与膨胀变形(或膨胀率)、上覆荷载之间的关系。
本文拟结合室内试验结果分析土体膨胀率与上覆荷载的相关关系。采用膨胀力试验中的加压膨胀法可以分析土体膨胀率与上覆荷载的相关关系,即对侧限状态下的土样施加不同大小的上覆荷载p,然后注水使土体发生膨胀,测得不同上覆荷载作用下土体的膨胀变形率,从而分析两者之间的相关关系。已有结果表明[14],土体膨胀率εep、无膨胀变形的竖向膨胀力Pv与上覆荷载p之间大致可拟合为如下数学关系:
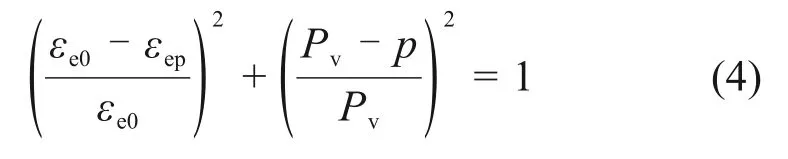
式中:εe0为上覆荷载为0 kPa 时的膨胀率,此时,εe0接近最大膨胀率;εep为上覆荷载为p时的土体膨胀率。上覆荷载p与土体膨胀率εep之间关系曲线如图4所示。从图4可以看出:不同含水率的土样呈现出不同的分布曲线特征;土体膨胀率与上覆荷载之间相关关系主要由土体自身性质以及初始含水率所决定。在相同条件下,土体初始含水率越小,含水率变化量越大,膨胀率越大。
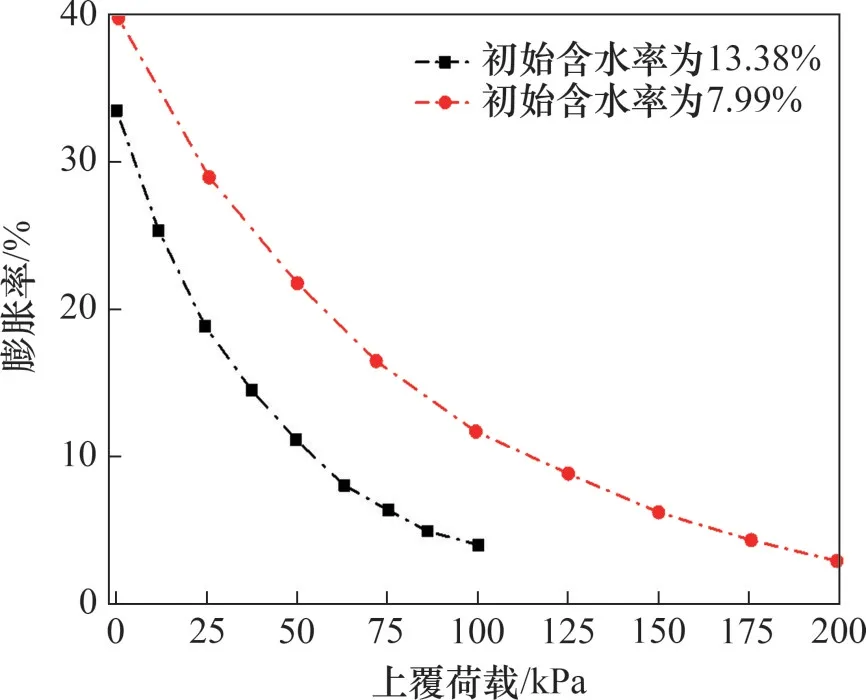
图4 上覆荷载p与膨胀率εep之间的关系Fig.4 Relationship between overburden load p and expansion rate εep
通过室内试验可以得到不同上覆荷载作用下膨胀土的变形规律,以及膨胀率为0时膨胀土的竖向膨胀力Pv。但在自然状态下,膨胀土难以被完全约束变形,更多的是膨胀土既存在一定的膨胀变形,也存在一定大小的竖向膨胀力。因此,尚需获得竖向膨胀力Pvε与土体膨胀变形εep之间的相关关系。目前,多采用侧限压缩试验来获得竖向膨胀力与土体膨胀变形的相关关系。在试验过程中,土样处于完全水平侧限状态,水平膨胀变形受到限制,土体膨胀率体现为土体的竖向膨胀变形。通过配制不同初始含水率的膨胀土试样,可以得到竖向膨胀力Pvε随土体竖向膨胀率εep的变化曲线[15],如图5所示。从图5可以看出竖向膨胀力Pvε随土体膨胀率增大而不断减小。对这种变化曲线进行数据拟合,可以得到竖向膨胀力Pvε与膨胀率εep之间的线性相关关系,即
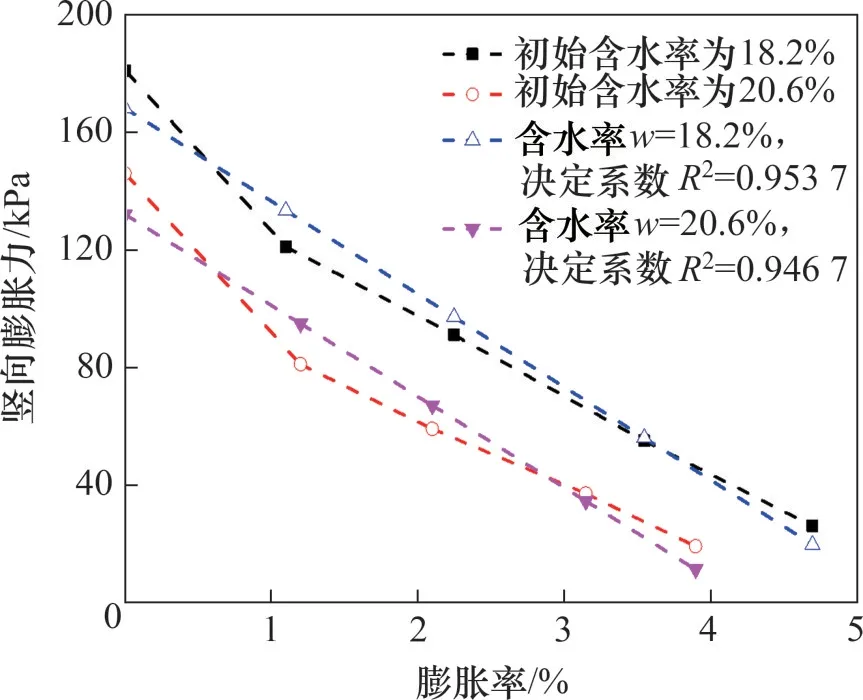
图5 竖向膨胀力Pvε与膨胀率εep之间的关系Fig.5 Relationship between vertical swelling pressure Pvε and expansion ratio εep

式中:Pvε为膨胀率为εep时的竖向膨胀力;k为斜率。斜率k与截距a均与土体自身性质和初始含水率有关。当土体的膨胀率εep≈0时,竖向膨胀力Pvε=Pv,因此,a=Pv,式(5)也可写成

由式(6)可知,当εep=εe0时,上覆荷载p=0,土体膨胀率将达到较大值,竖向膨胀力Pvε≈0,因此,有

且
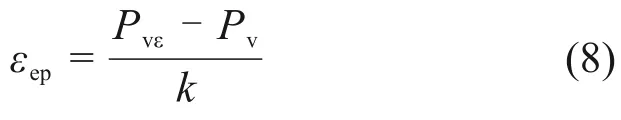
联立式(7)和式(8)可得
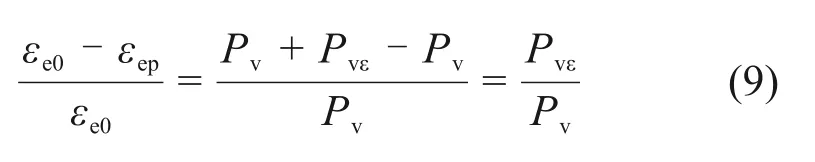
将式(9)代入式(4)可得
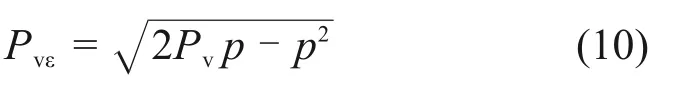
将式(3)代入式(10)可得
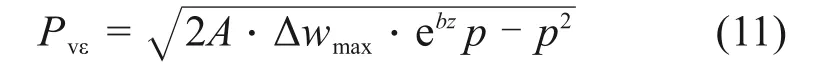
当土体可视为半无限弹性空间体时,上覆荷载p可按p=γ·z计算。
1.3 水平膨胀力的计算方法
膨胀土因胀缩作用会同时产生水平和竖向膨胀力。水平膨胀力与竖向膨胀力之间存在明显的正相关性[16-18]。竖向膨胀力的计算应同时考虑含水率变化和土体上覆荷载,并由此建立竖向膨胀力计算公式,因此,只需明确竖向膨胀力与水平膨胀力之间的相关关系,便可得到水平膨胀力的计算方法。在侧限条件下,水平膨胀力与竖向膨胀力之间的数学关系可按弹性理论进行推导,即

式中:μ为膨胀土的泊松比;Phε为水平膨胀力。
膨胀土的泊松比μ通常由土工试验来确定[19-20]。一般而言,膨胀土泊松比μ并非固定不变,而与膨胀土的初始含水率呈现出一定的线性相关关系,如图6所示。当无试验数据时,膨胀土泊松比μ可按经验取值,如王年香等[14]推荐膨胀土泊松比取值为μ=0.4。
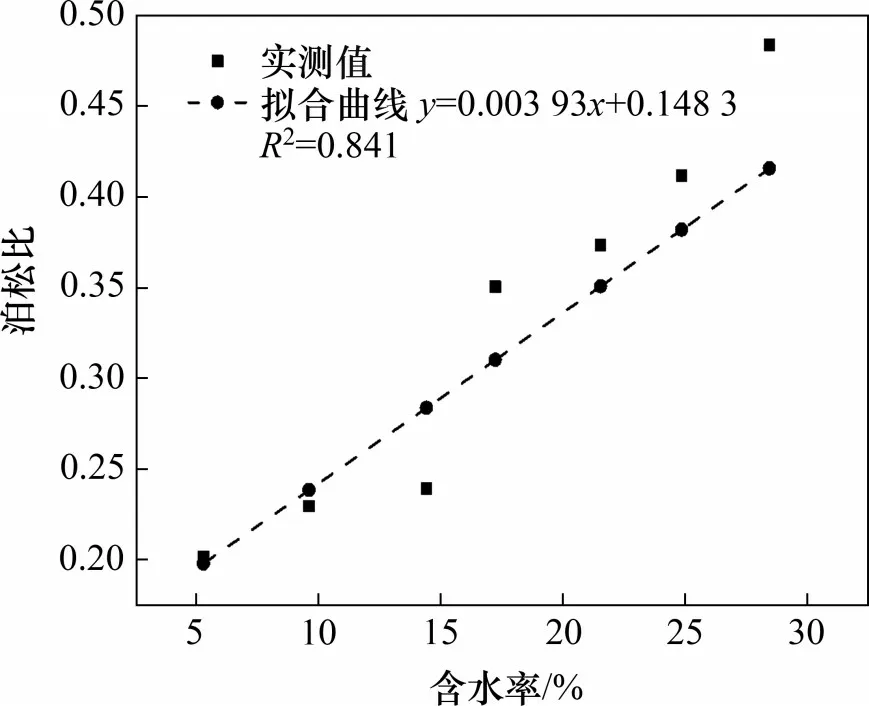
图6 泊松比与膨胀土含水率的相关关系Fig.6 Correlation between Poisson's ratio and water content of expansive soil
将式(11)代入式(12)可得
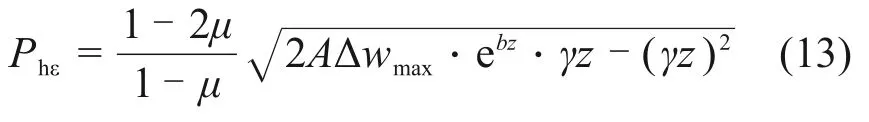
式(13)即为考虑含水率变化量和上覆荷载影响的水平膨胀力Phε的计算公式。将式(3)代入式(13),水平膨胀力Phε也可写成如下形式:
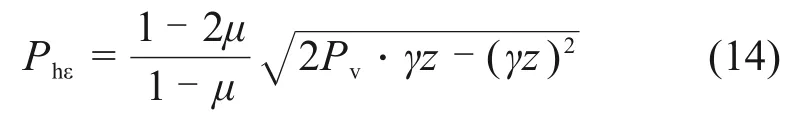
1.4 桩板结构水平膨胀力分布形式
对于桩板结构支护膨胀土边坡,桩板结构将约束膨胀土的侧向膨胀变形,膨胀土会因膨胀反应而产生水平膨胀力。确定水平膨胀力大小及其分布形状是对桩板结构支护膨胀土边坡进行工程设计的首要内容。
水平膨胀力沿深度方向呈非线性分布,且计算公式比较繁琐。为验证水平膨胀力计算公式的合理性,并据此对水平膨胀力计算方法进一步提炼和简化,以获得适用于桩板结构支护膨胀土边坡工程设计的实用计算方法。通过室内模型试验对桩板结构的水平膨胀力进行测试,并据此分析桩板结构的水平膨胀力分布特点。
1.4.1 室内模型试验简介
模型试验以南昆高速铁路那百段膨胀土为填料,模拟外界雨水浸入桩板结构墙后膨胀土的工况,并测试膨胀土的水平膨胀力。模型长×高×宽为4 m×2.1m×1.5m,膨胀土的主要物理力学指标如表1所示,根据GB 50112—2013“膨胀土地区建筑技术规范”的相关条文要求,可确定其为中等膨胀土。

表1 南昆铁路膨胀土基本物理指标Table 1 Basic physical indexes of expansive soil in Nanning-Kunming Railway
试验采用南昆高速铁路那百段膨胀土进行室内模型填筑,在填筑过程中预留若干砂井以便于外部雨水渗入。沿不同垂直深度埋设土压力盒,测试膨胀土在桩板结构后产生的水平膨胀力。
1.4.2 试验结果与分析
桩板结构后不同深度处的水平膨胀力测试结果如表2所示。将深度以最大深度170 cm 为分母进行归一化处理,水平膨胀力以最大水平膨胀力27 kPa为分母进行归一化处理,可得到归一化后的水平膨胀力沿深度的分布规律。为便于分析,本文将张颖钧等[3-6]提出的方法一并列入对比,如图7所示。不同方法得到的水平膨胀力沿深度分布结果与试验测试结果均存在一定偏差。但总体而言,本文给出的水平膨胀力分布理论结果与试验测试结果具有良好的一致性,验证了水平膨胀力理论方法的合理性。
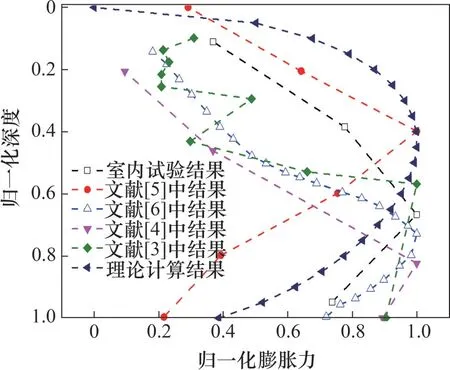
图7 归一化处理后的水平膨胀力分布Fig.7 Normalized distribution of lateral swelling pressure
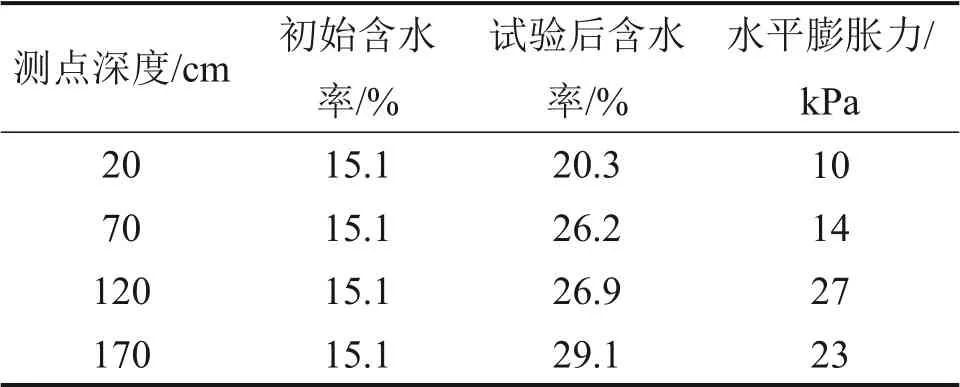
表2 膨胀土水平膨胀力模型试验结果Table 2 Model test results of lateral swelling pressure of expansive soil
对桩板结构支护膨胀土边坡进行工程设计时,应提炼简化形成一个便于设计计算的实用方法。在进行工程设计时,主要考虑大气影响深度范围内的水平膨胀力作用。结合桩板结构水平膨胀力的试验结果和理论方法,可将水平膨胀力沿深度的分布规律进行相应简化,如图8所示。其中,h为水平膨胀力分布形状拐点的深度,H为大气影响深度,L为抗滑桩悬臂段高度。水平膨胀力沿深度逐渐递增,当达到某一拐点后,水平膨胀力沿深度递减。这种分布形式可称为“反K形”分布。
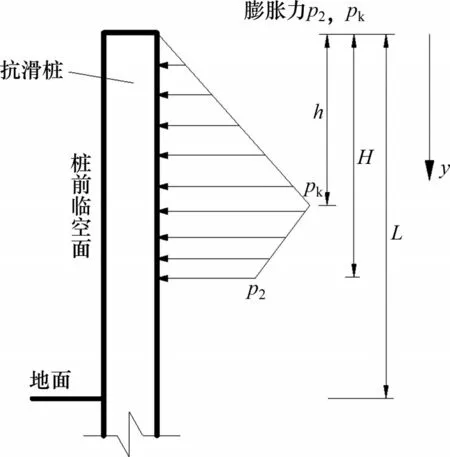
图8 水平膨胀力“反K形”分布Fig.8 Inverse K-type distribution of lateral swelling pressure
对水平膨胀力的“反K 形”分布可结合桩板结构支护膨胀土边坡的实际工作性状进行说明。桩板结构后填土面顶部若没有上覆荷载,则土体能够比较充分地发生垂直方向的膨胀变形,竖向膨胀力能得到释放,相应地,水平膨胀力将趋于0 kPa,因此,对于“反K形”分布,当深度z=0 m时,水平膨胀力也为0 kPa。“反K形”分布存在1个拐点,即对应于式(13)所示函数的1 个极值点。假设拐点的深度为h,可通过对式(13)进行极值求解来获得h的具体数值。在分布拐点以下深度,为便于桩板结构水平膨胀力计算,可假定水平膨胀力沿深度方向呈线性递减。该假定的合理性将通过现场实例验证。
确定图8所示的水平膨胀力沿深度“反K 形”分布规律的关键在于确定拐点深度h、拐点处的水平膨胀力Pk以及大气影响深度H处的水平膨胀力P2。通过对式(13)求极值,可得到拐点深度h的计算方程:
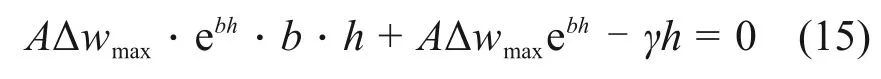
将式(3)代入式(15)可得:

由式(16)可知,h受膨胀率为0 时的竖向膨胀力Pv、土体重度γ和含水率变化量分布系数b等参数的影响。各个参数的具体数值可结合试验或现场监测结果确定。将深度z=h代入式(14),可以得到拐点处的水平膨胀力Pk。对于大气影响深度H处的水平膨胀力P2,同样可令z=H代入式(14)进行求解。因此,该理论方法具备良好的可操作性。
本课题组提出采用矩形分布、三角形分布和倒三角形分布等形式来表征水平膨胀力沿深度的分布规律。实际上,矩形分布、三角形分布和倒三角形分布均可统一表征为梯形分布的形式。水平膨胀力梯形分布的分析模型如图9所示。在梯形分布中,顶部水平膨胀力P1和底部水平膨胀力P2是需要确定的主要参数。当P1=0 且P2≠0 时,梯形分布可转化为三角形分布;当P1=P2时,梯形分布转化为矩形分布;当P1≠0,P2=0 时,梯形分布则转化为倒三角形分布。
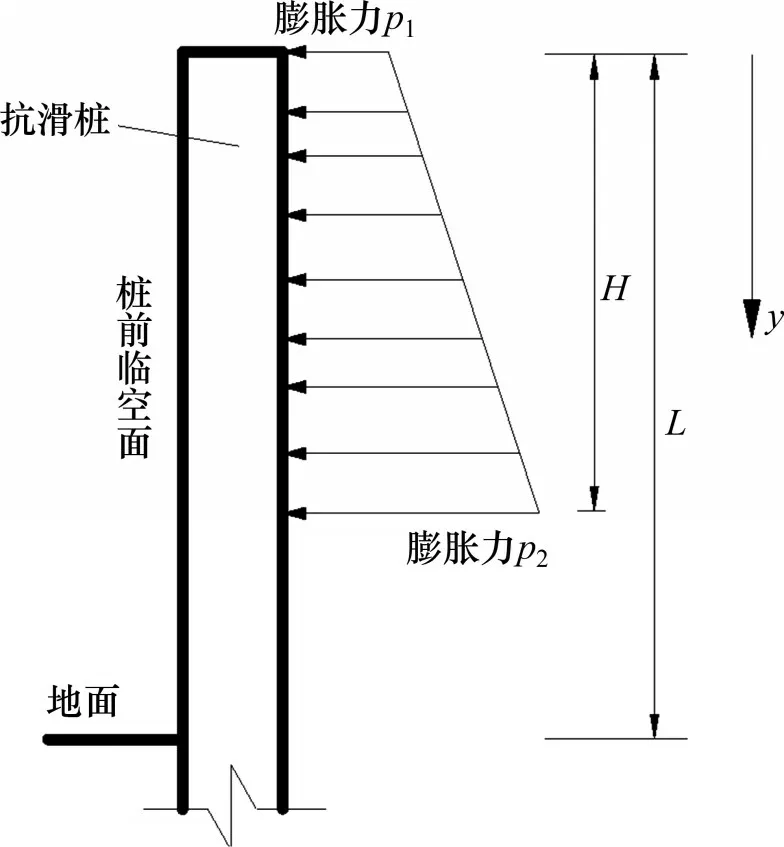
图9 水平膨胀力的梯形分布Fig.9 Trapezoidal distribution of lateral swelling pressure
本文基于水平膨胀力的“反K 形分布”和梯形分布等假定,推导膨胀力作用下桩板结构的桩身内力计算公式,并通过工程实例的实测结果进行对比和分析。
2 水平膨胀力作用下桩板内力计算
2.1 水平膨胀力“反K形”分布
对于桩板结构支护膨胀土边坡,进行桩板结构内力计算时需考虑膨胀土的水平膨胀力作用效果,可在传统计算公式的基础上,将水平膨胀力作为一种外荷载进行修正。大量观测结果表明,膨胀土膨胀反应引起的膨胀力影响范围主要在大气影响深度0~H范围内,因此,只需考虑大气影响深度0~H范围内的水平膨胀力作用。对于桩板结构而言,桩身悬臂段长度L的合理确定是工程设计考虑的主要因素。长度L主要由桩板结构的桩身内力控制。
当水平膨胀力沿深度分布形式按“反K 形”考虑时,桩板结构的桩身内力计算图式如图8所示,由此可计算桩身剪力和桩身弯矩。设y为桩身计算截面所在的深度(自桩顶算起),Qp为桩身计算截面剪力,Mp为桩身计算截面弯矩。
当0≤y≤h时,
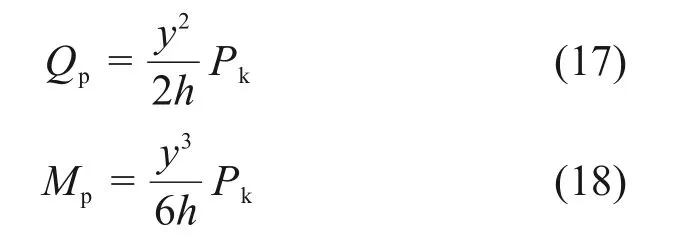
当h<y≤H时,
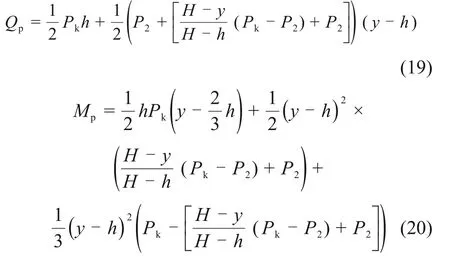
当H<y≤L时,
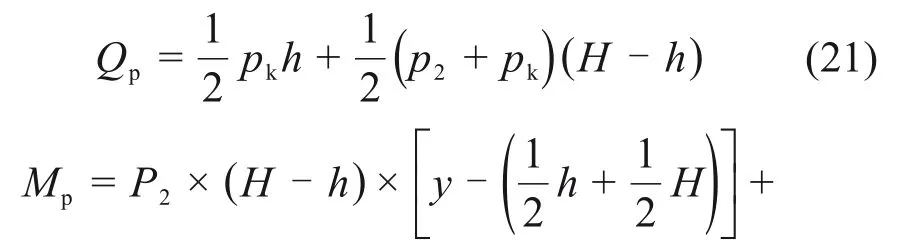
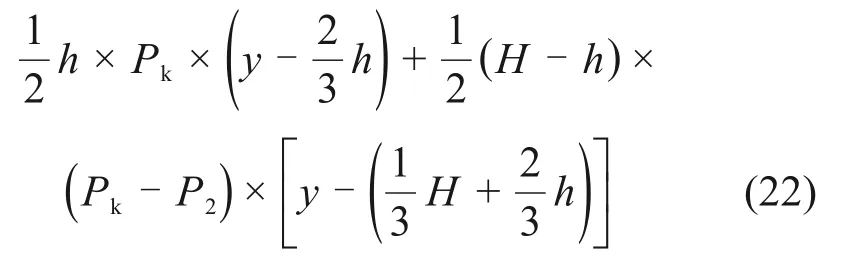
2.2 水平膨胀力梯形分布
当水平膨胀力沿深度分布形式按梯形分布考虑时,桩板结构的桩身内力计算图式如图9所示,由此可得到桩身剪力Qp和桩身弯矩Mp的计算公式。
当0≤y≤H时,
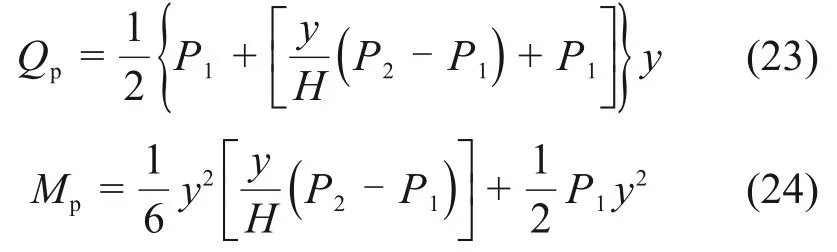
当H<y≤L时,
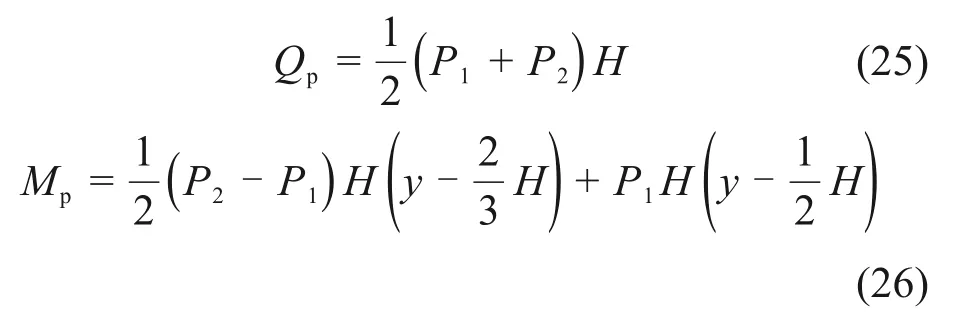
3 工程实例分析与对比
3.1 工程背景
南昆铁路广西百色市火车站附近,表层以下厚度为3~9 m的土为中等膨胀土。铁路线路右侧为膨胀土高边坡桩板支挡结构工程,如图10所示。根据现场资料可知,土体重度γ=19 kN/m3,大气影响深度H=4 m,桩体悬臂段长度L=4 m。选取膨胀土边坡桩板结构的典型桩体进行现场监测,监测时间为2020-04-30—2020-08-14。在桩后填土内埋设若干土压力盒测试桩身结构在长期服役过程中的土压力变化;在桩后填土大气影响深度0~4 m范围内埋设土壤湿度计,以监测土体含水率的变化情况;沿桩身等间距布置应变计,以监测桩身应变情况,并据此推算桩身的弯矩分布规律。

图10 南昆铁路百色段右侧膨胀土高边坡桩板结构Fig.10 Pile-sheet structure supporting high expansive soil slope on the right side of Baise Section in Nanning-Kunming Railway
3.2 对比分析
现场测试中对膨胀土水平膨胀力的监测通常有2种处理方法。
第一种方法为监测桩板结构服役期间的桩后土压力,然后将实测土压力减去由库仑主动土压力公式等方法得到的理论值,由此推算水平膨胀力。考虑到实际工程中土压力测试结果往往误差偏大,加之影响因素甚多,且土压力理论公式又进行了很多简化,得到的水平膨胀力结果偏差往往较大。
第二种方法认为,工程实践中桩板结构的损伤主要是膨胀土中含水率增大而引起的水平膨胀力所致,因此,对桩板结构后的侧向压力进行长期监测,并假定因土体自重引起的土压力基本保持不变,水平膨胀力则主要由膨胀土含水率变化而产生。为简化计算,可采用雨季(土体趋于饱和)的侧向压力实测值减去旱季(土体相对干燥)的侧向压力实测值,作为含水率变化引起的水平膨胀力最大值。
本文采用第2 种方法分析膨胀土的水平膨胀力。结合现场监测期间的气候条件、土壤湿度和土压力测试结果,可推算膨胀土的最大竖向膨胀力为225 kPa。关于膨胀土含水率变化量分布系数b,可根据桩后大气影响深度范围内(0~4 m)膨胀土含水率变化量沿深度分布情况进行推算,如图11所示。基于膨胀土含水率变化量沿深度呈负指数分布的基本假设,可以确定含水率变化量系数b为-0.407 4。
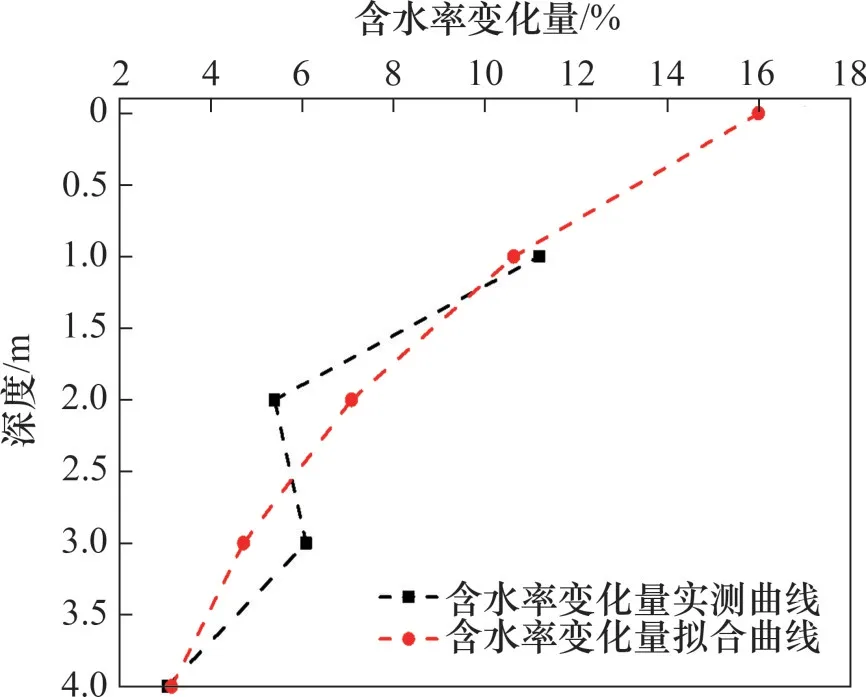
图11 膨胀土含水率变化量沿深度分布情况Fig.11 Distribution of water content variation of expansive soil along depth
根据现场测试结果,土体重度γ=19 kN/m3,大气影响深度H=4.0 m。令Pvmax=225 kPa,代入式(15)可得拐点深度h=1.73 m。分别令z=h和z=H,并代入式(14)可得Pk=26.29 kPa,P2=10.15 kPa。由此可基于水平膨胀力“反K形”分布的基本假设,计算桩身的剪力或弯矩。
为便于比较,将水平膨胀力矩形分布、三角形分布和倒三角形分布等假定的弯矩计算结果一起进行对比[21],如图12所示。从图12可以看出:水平膨胀力的4种分布假定的弯矩计算结果与弯矩实测值的变化规律大体一致,且弯矩实测值均位于水平膨胀力的4种不同分布假定的弯矩计算结果包线以内。由此表明,水平膨胀力的4种分布形式假定均能较好地反映桩板结构的桩身实际受力情况。相比而言,基于水平膨胀力沿深度“反K形”分布假定的弯矩计算结果更接近桩身弯矩的实测结果。因此,本文提出的水平膨胀力“反K 形”分布的分析方法具有合理性和有效性。基于水平膨胀力“反K 形”分布的桩板结构分析方法可为工程设计提供借鉴和参考。
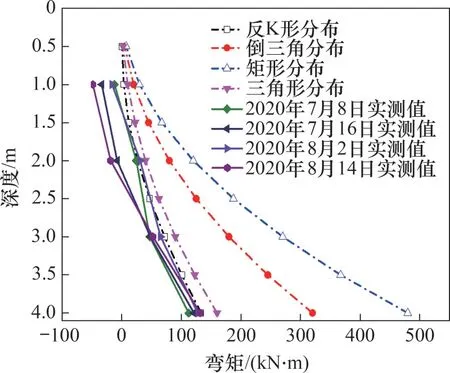
图12 不同水平膨胀力分布形式引起的弯矩计算值与实测值对比Fig.12 Comparison of calculated and measured bending moment caused by different lateral swelling pressure distributions
4 结论
1)通过分析膨胀土竖向膨胀力与含水率变化量、上覆荷载和膨胀率的相互关系,探讨水平膨胀力的计算方法。开展桩板结构水平膨胀力的室内模型试验,结合试验结果提出膨胀土边坡桩板结构水平膨胀力沿深度“反K形”的分布模式。
2)基于膨胀土水平膨胀力沿深度“反K 形”分布、三角形分布、倒三角形分布和矩形分布等基本假定,推导了桩板结构的桩身剪力、桩身弯矩计算公式。
3)结合膨胀土边坡桩板结构的现场测试结果,对水平膨胀力沿深度“反K 形”分布、三角形分布、倒三角形分布和矩形分布的计算结果进行了对比分析,验证了水平膨胀力“反K 形”分布假定的合理性和有效性。
