高动态跳频载波跟踪技术

刘 艺, 周晓雄, 程广俊

(北京遥感设备研究所, 北京 100854)

0 引 言

复杂的战场环境下,无人机、导弹等高速飞行体在高动态环境下的通信问题已日益成为研究热点。为了保障战场作战与指挥,无线电通信日益成为了战场上通信的重要手段。但无线电通信容易受到不同类型的干扰,尤其对于短波通信领域,不但会遭到雷电、工业等自然干扰,而且敌方人为的跟踪、阻塞、多径干扰等各种通信干扰也会影响其正常通信,所以提高短波通信抗干扰能力和通信性能,成为了无线电通信技术的首要任务,扩频通信中的跳频通信技术由于具有很强的抗搜索、抗截获、抗干扰能力,成为了无线通信中重要的抗干扰手段。在无线电通信中,高动态环境是指收发双方具有较高相对运动速度的应用场景。在高动态的环境中,无人机或导弹之间存在着较大的相对速度、加速度和加加速度,这将会产生较大的多普勒频移及其高阶量,使得高动态下的载波跟踪成为系统的关键技术难点之一。

国内外针对于高动态下的载波跟踪技术已取得了一定的技术进展。同理，载波跟踪是载波同步中的关键。载波跟踪的锁相环结构就是利用窄带跟踪滤波器跟踪输入信号载波的频率与相位的变化,窄带跟踪滤波器的输出就是需要提取的放大的载波信号。载波跟踪技术结构中最广泛使用的是科斯塔斯锁相环,但由于环路在高动态环境下会发生抖动、频率周期滑动,从而导致跟踪相位的不连续,同时噪声也会增大环路抖动,故而涌现了一些载波跟踪锁相环环路的改进方法。然而，这些方法需增大环路带宽来提高动态性能。此外,更多的噪声会通过环路滤波器降低跟踪精度,尤其是在低载噪比的情况下,大的噪声功率会使载波跟踪环失锁。纵观前人的研究,可知解决这一矛盾的方式即在传统结构中嵌入算法或改进环路结构提高环路对动态环境的容忍度。目前流行的一种最优的估计方法是卡尔曼滤波,它利用实时状态估计减少噪声的影响,不断地递推、修正估计过程,得到关于状态变量的一个最优估计。该方法运算过程中数据量小,可用于动态实时场景。

传统跳频系统的载波跟踪利用收发双方预先知道的跳频图案和当前运动载体速度测量值估计出下一个跳频驻留时间开始时刻引入的多普勒捷变量,并把它及时补偿到跟踪环路的数字控制振荡器(numerically controlled oscillator,NCO)调整误差量中,极少涉及结合卡尔曼滤波算法的高动态环境下的载波跟踪。本文首先简要介绍了目前广泛应用的跳频系统载波跟踪结构;针对跳频的突发传输、高动态环境等特点提出开环估计协同闭环扩展卡尔曼滤波的载波跟踪方法,能够快速锁定载波频率,适应高动态环境能力强,不易失锁、无需增大环路带宽,从而使得进入滤波器的噪声变小。同时,基于最大似然估计(maximum likelihood estimation， MLE)的开环估计对精确锁定载波有着重要作用。

1 跳频系统载波跟踪简介

战场环境中为了保证通信不被干扰,常采用跳频系统进行抗干扰。跳频通信系统广泛使用时分多址(time division multiple access, TDMA)技术,突发模式传输是其主要的技术特点,但以突发模式传输,接收到的信号只持续有限的一段时间,这就要求载波的同步捕获跟踪必须在有限的时间内处理完。传统科斯塔斯锁相环路由于其较高的锁频稳定性得到了广泛的应用,考虑到战场环境的高动态,引起载波环多普勒频移的因素有:① 导弹、无人机等载体自身运动和不规则的振动带来的多普勒频率偏移和多普勒变化率;② 跳频跳变可能带来的多普勒频偏的异常大值。这两方面因素致使载波环路变得难以锁定甚至失锁。为了解决这一难题,有学者提出了基于跳频图案辅助的科斯塔斯锁相环,它根据当前跳频点的弹体速度和对应时刻的载波频率,预测出下一个跳频点处的多普勒变化值,当切换到下一个跳频点时,在环路中累加预测出的多普勒变化值,从而避免由于载频高阶变化量带来的环路瞬变,使环路始终处于稳态。捕获模块提供的弹体初始速度可用于跳频图案辅助,即当多普勒变化量不超过系统跟踪带宽,用当前多普勒变化量预测下一帧变化,并用于跟踪捕获时的多普勒变化量补偿,以此提高跟踪补偿算法在高动态下的容忍能力,环路的原理如图1所示。

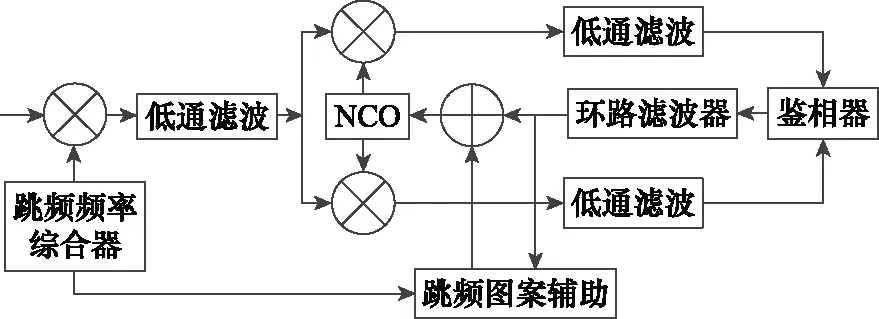
图1 基于跳频图案辅助的载波跟踪环路Fig.1 Carrier tracking loop based on frequency hopping pattern

这种改进措施只适用于载体机动能力差、多普勒频移较小且不存在高阶频率变化的情况。由于无人机、导弹间有着相对高的运动速度及其一阶、二阶变化量,会导致在载频上引起很大的多普勒频移甚至更高阶的频移变量。此时，若继续采用传统的科斯塔斯锁相环路,则必须增大载波跟踪环的噪声带宽以适应高动态环境,但环路噪声带宽的增加必然导致环路滤波器进入更多的信号带外噪声,使载波跟踪精度大大降低,若环路接收低载噪比信号时,噪声平均幅值大于所设门限从而导致频率检测精度下降、测频误差大。为此,本文提出了有效解决上述问题的改进跳频系统高动态载波跟踪算法,不但保证了跟踪精度,而且可以快速锁定频率。

2 改进的跳频系统高动态载波跟踪

第1节提及的传统载波跟踪环路只适用于较低动态环境,对实时性和精度的要求较低,虽然采用跳频图案辅助对载波频率进行辅助估计,但是在高动态环境下,这种估计的精度较低,误差也相对较大。本文介绍一种基于开环MLE估计和闭环扩展卡尔曼滤波器的高动态载波跟踪算法,在高动态、低载噪比下,实时性和精度有着大幅度的提升。依托传统的科斯塔斯环路结构设计,设计出一种开环MLE估计和闭环扩展卡尔曼结构相结合的跟踪环路结构。扩展卡尔曼滤波器具备滤波器和鉴相器的双重功能,但扩展卡尔曼算法对非线性有一定适应性,提高了跟踪算法二阶或三阶动态适应性和载波相位跟踪精度,从一定程度上弥补了传统环路带宽限制的影响,且能够在低载噪比时精确估计出高动态信号的多普勒变化,从而对高动态信号实现高精度稳定跟踪。环路的结构如图2所示。

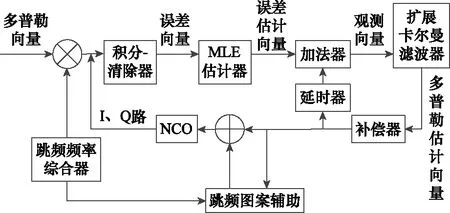
图2 改进的跳频系统高动态载波跟踪环路Fig.2 Modified high dynamic carrier tracking loop for frequency hopping system

如图2所示,I、Q两路由于其表达式相似,故而统一用同一个表达式来表示,下面各式均依此处理。设环路的输入信号可表示为含有加性高斯白噪声的两路正交数字中频载波信号

()=cos[2π(+)/f+]+()

(1)

式中:为幅度;为离散时间;为采样率;为初始相位;()为单边功率谱密度为、噪声方差为2的零均值高斯白噪声，表示下变频后的中频信号；表示高动态环境下无人机、导弹间的运动在接收信号载波频率上引起的时变多普勒频移,将它以向量参数表示为

=[]

(2)

式中：为多普勒向量;、、分别表示多普勒频偏及其一阶变化率、二阶变化率,单位分别为Hz、Hz/s、Hz/s。

两路正交的本地数字载波信号由NCO产生,可表示为(设初相为0)

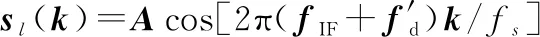
(3)

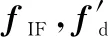
(4)

输入中频信号、本振频率信号和跳频频率综合器产生的信号，经过积分运算处理后,得到两路正交的跟踪误差信号,可表示为

()=cos[2πΔT+]+()

(5)

式中:为采样时间;为积分时间;为初始相位;()表示噪声方差为2的热噪声；Δ表示频偏跟踪误差,将它以向量参数表示为

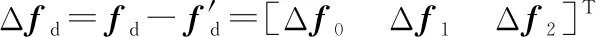
(6)

我们将Δ称为误差向量。将两路正交的跟踪误差信号采样合成复采样误差信号,接着采样误差信号向量被送入MLE估计器,其输出信号即为误差估计向量:

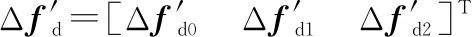
(7)

加法器的功能是将误差估计向量与前一个跳频驻留时间内补偿器输出的多普勒频偏累加,得到当前时刻对多普勒频偏的观测向量。环路的频率跟踪设计中不可或缺的部分就是积分过程,而此处的加法运算即完成对频偏跟踪误差量的积分。

卡尔曼滤波器的作用是将观测向量中的热噪声降到最低,实现最佳的状态估计。滤波的输出是多普勒估计向量,是对多普勒频率参数向量的状态估计,此时的卡尔曼滤波器的模型可表示为

(+1)=()+()

(8)

()=()+()

(9)

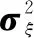
(10)

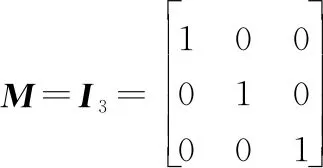
(11)

卡尔曼滤波的状态参数估计(即多普勒估计向量″)和误差估计量可由下列公式组计算：

″(+1|)=″(|)

(12)

(+1|)=(|)+

(13)

(+1)=(+1|)((+1|)+)

(14)

″(+1|+1)=″(+1|)+(+1)[-″(+1|)]

(15)

(+1|+1)=[-(+1)](+1|)

(16)

式中:为单位矩阵；噪声过程()和()的方差阵和可分别表示为

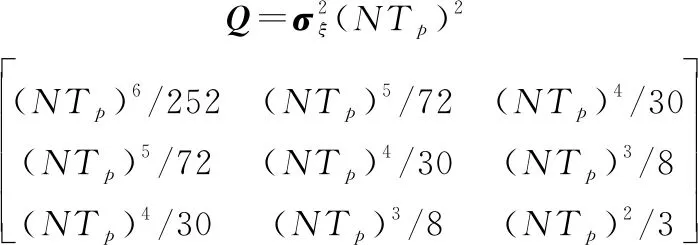
(17)

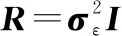
(18)

而采用扩展卡尔曼滤波器最低化热噪声的影响,同时其增益表达式中的雅克比矩阵包含了滤波器系数的权重,使得输入测量值和预测测量值的差值达到最优化。

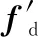
(19)

3 性能仿真结果与分析

针对高动态环境下的跳频系统,分别采用传统的科斯塔斯环路跟踪及本文所提改进的开环MLE估计和闭环扩展卡尔曼结构环路进行载波跟踪。仿真条件如下:初速度=300 m/s,初速度的一阶变化量初值=15,初速度的二阶变化量初值=60s,=98 m/s,高动态模型如图3所示。

图3 高动态模型Fig.3 High dynamic model

图4给出了采用开环MLE估计和传统科斯塔斯环路结合跳频图案对跳频信号在高动态下载波频率估计的绝对偏差,可以看出采用开环MLE估计可以更准确地估计出多普勒频率,使得实际载波频率和估计的载波频率绝对误差进一步减少,从而确保环路能够快速锁定频率。

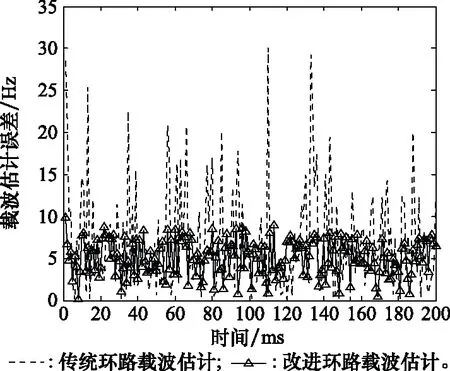
图4 高动态下载波频率估计的绝对偏差对比Fig.4 Absolute deviation comparison of carrier frequency estimation for high dynamic scene

下面将分别在高载噪比50 dB-Hz和低载噪比23 dB-Hz这两种情况下,比较上述两种跟踪环路对载波的跟踪结果。

3.1 载噪比为50 dB-Hz

图5是传统环路在高载噪比50 dB-Hz的条件下载波多普勒频率的跟踪结果,从仿真结果可以看出科斯塔斯环路可快速收敛跟踪并能同步稳定跟踪,图6是本文改进设计新环路在高载噪比50 dB-Hz的条件下载波多普勒频率的跟踪结果,从仿真结果可以看出与传统环路在高载噪比下跟踪性能相差不大。在高载噪比的条件下,不同环路在跟踪性能上的差距不大。从本次仿真选取了如表1所示的10组典型数据,通过比较可以看出改进新环路的跟踪误差更小、性能稍佳。

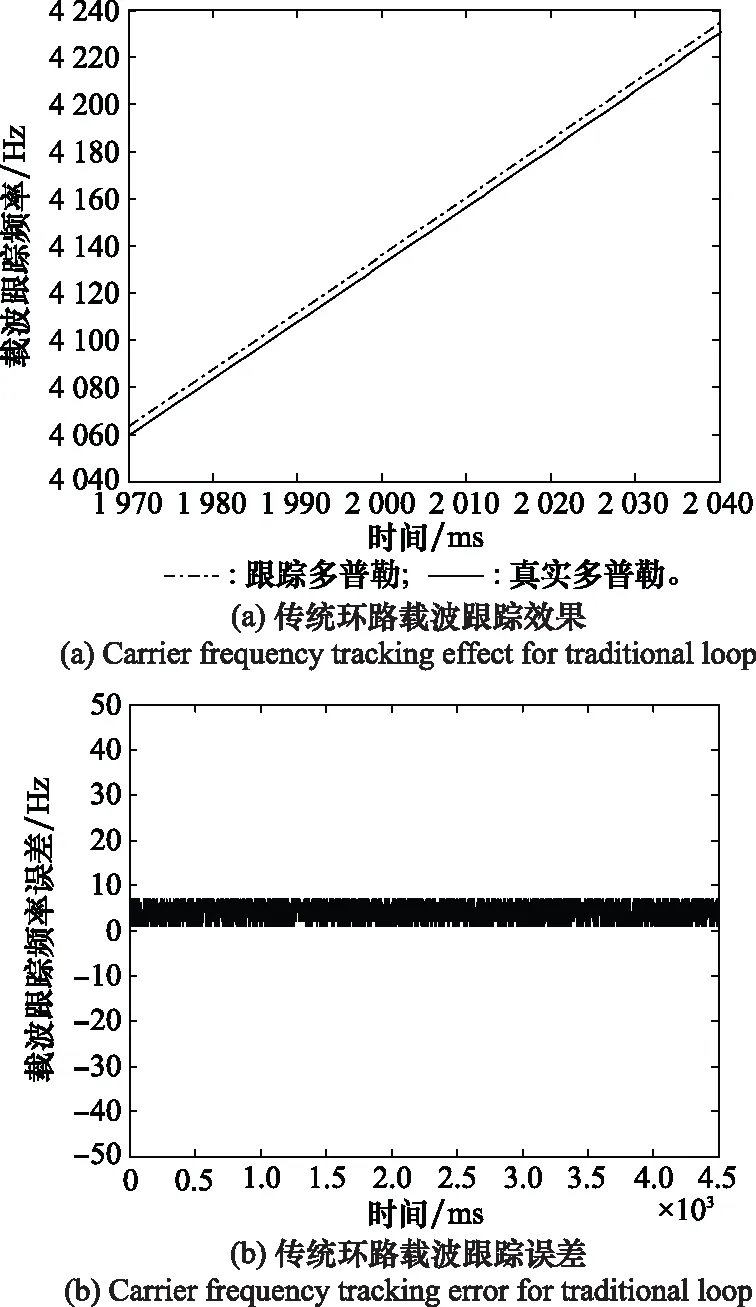
图5 传统环路跟踪效果和跟踪误差Fig.5 Tracking effect and tracking error for traditional loop

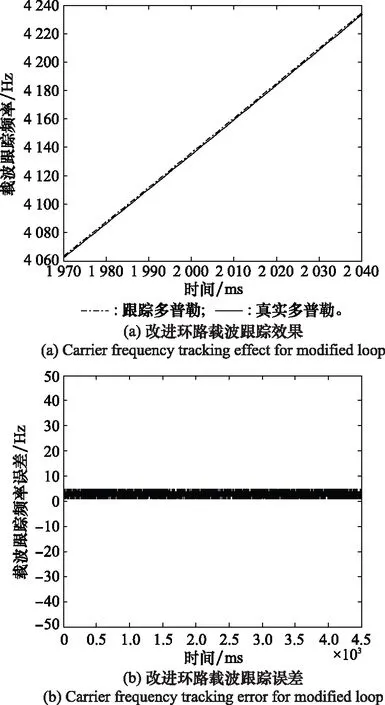
图6 改进环路跟踪效果和跟踪误差Fig.6 Tracking effect and tracking error for modified loop

表1 载噪比为50 dB-Hz时多普勒频率跟踪误差绝对值

3.2 载噪比为23 dB-Hz

图7是传统环路在低载噪比23 dB-Hz的条件下载波多普勒频率的跟踪结果,从仿真结果可以看出科斯塔斯环路随着时间渐渐失稳,跟踪误差越来越大,可以看出传统环路在低载噪比下跟踪失效。图8是本文改进设计新环路在低载噪比23 dB-Hz的条件下载波多普勒频率的跟踪结果,从仿真结果可以看出在低载噪比下跟踪性能良好、精度较高且具有优良的收敛跟踪时间,本次仿真选取了如表2所示的10组典型数据,通过比较可以看出改进新环路具有较低的跟踪误差、极短的跟踪响应,因此本文所设计的基于扩展卡尔曼滤波算法环路具有更高的适应能力和扩展能力。

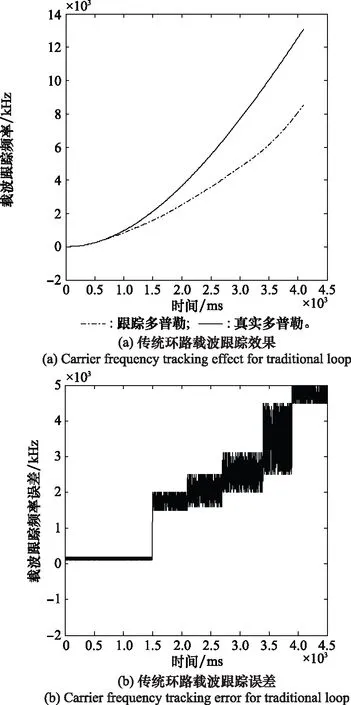
图7 传统环路跟踪效果和跟踪误差Fig.7 Tracking effect and tracking error for traditional loop

图8 改进环路跟踪效果和跟踪误差Fig.8 Tracking effect and tracking error for modified loop

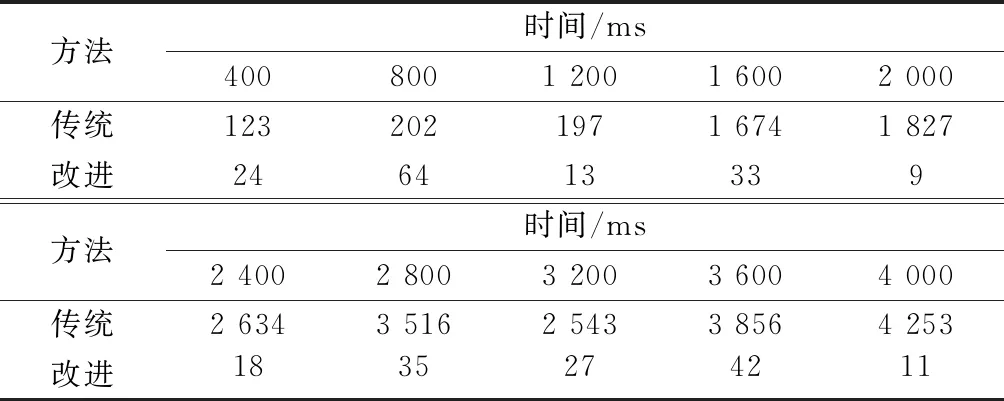
表2 载噪比为23 dB-Hz时多普勒频率跟踪误差绝对值

最后图9给出了载噪比为35 dB-Hz时锁定跳频频率为3.563 MHz的载波曲线图,可以看出采用改进的载波环路在同等条件下可以迅速地锁定载波频率。

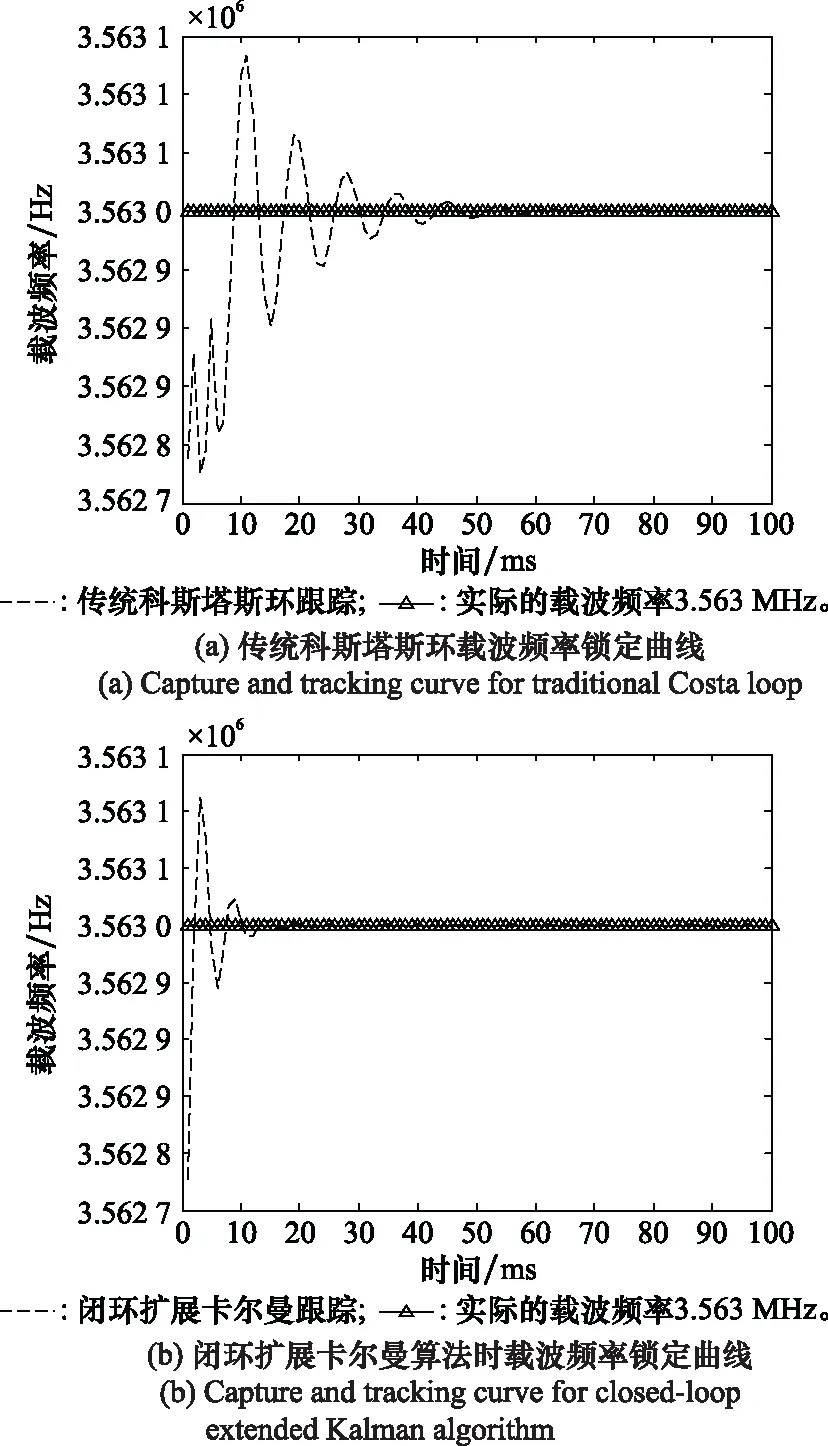
图9 载噪比35 dB-Hz载波频率锁定曲线Fig.9 Capture and tracking curve of carrier frequency as carrier noise ratio is 35 dB-Hz

4 结 论

本文在查阅国内外高动态载波跟踪技术的基础上针对通信抗干扰的跳频系统突发传输的特点,提出了开环MLE估计和闭环扩展卡尔曼滤波的跟踪环路结构,克服了传统环路的缺点,经仿真和分析得出结论:改进的环路能够快速稳定地跟踪高动态下的跳频载波信号且跟踪精度较高,除此之外,在相同条件下跟踪误差要小于传统科斯塔斯环路,尤其是在低载噪比下,优势更加明显。因此,新设计的环路可以更加适应高动态环境下的载波跟踪。