基于视差范围估计和改进代价的半全局匹配

彭 妍, 郭君斌,*, 于传强, 李静波

(1. 火箭军工程大学导弹工程学院,陕西 西安 710025; 2. 中国人民解放军96873部队,陕西 宝鸡 721000)

0 引 言

立体匹配通过寻找左右图像中的同名点,计算视差,从而获取物体的深度信息。近年来,随着立体匹配技术的发展,立体匹配已被广泛应用在三维重建、目标检测、自动驾驶、虚拟现实等领域。Scharstein等人在总结之前的立体匹配方法后提出了立体匹配的常规基本框架。在该框架中,立体匹配被划分为匹配代价计算、代价聚合、视差计算和视差优化4个步骤。根据计算策略的不同,传统立体匹配方法又可被分为局部、全局和半全局3类算法。其中,半全局匹配算法(semi-global matching, SGM)综合考虑了速度和精度对匹配的影响,应用最为广泛。

视差范围作为立体匹配中的一个重要概念,用来确定匹配点的候选范围,却没有得到传统SGM算法的重视。在实际场景中,立体图像对的视差范围通常不能预知,一般解决方法是人为地设定一个视差范围,但是这种方法比较主观,没有理论依据,得到的视差范围往往并不准确。若视差范围过大,导致计算资源浪费;若视差范围过小,容易导致视差计算错误。因此有效的视差范围估计在立体匹配中就显得尤为重要。

匹配代价计算作为立体匹配的第一步,为后续优化得到准确的视差值提供了基础。传统SGM算法通常采用Census变换进行代价计算,而传统Census变换仅考虑图像的亮度信息做Hamming距离计算匹配代价,在图像的重复纹理区域,计算结果具有模糊性,容易导致误匹配,进而影响视差计算精度。

针对视差范围通常不能预知的问题,毛苗等人提出了一种基于图像细分的快速视差范围估计算法;董本志等人在毛苗的基础上,提出了一种基于前向搜索的图像迭代细分方法来估计视差范围,得到更精确的视差范围;李海超等人利用特征点拟合空间平面,根据平面估计视差范围,有效提高了匹配的速度和精度;Yang等人使用金字塔匹配策略计算不同金字塔图像上每个像素的视差范围。

针对传统Census变换的问题,Mei等人提出了将灰度差绝对值和Census变换结合,提高了弱纹理和重复纹理区域的匹配精度;闫利等人提出了将梯度与Census变换结合,提高了弱纹理区域的匹配结果;Zhu等人提出了将Census变换、颜色和梯度作为混合匹配代价;Liu等人提出了将增强的图像梯度和改进的Census变换结合,对无纹理区域具有较好的鲁棒性。

针对传统SGM算法存在的不足,提出了一种基于视差范围估计和改进代价的半全局匹配算法。首先,采用二元稳健恒定可扩展关键点(binary robust invariant scalable keypoints,BRISK)、加速稳健特征(speeded up robust feature,SURF)和方向描述符(oriented brief,ORB)算子同时提取图像对的特征点,对所有特征点统一采用SURF描述子计算特征向量,通过快速最近邻搜索方法(fast library for approximate nearest neighbors,FLANN)进行特征点匹配,利用立体匹配的约束条件筛选匹配点,对筛选后的匹配点对计算视差值,估计图像的视差范围;然后,在估计好的视差范围内,分别对图像的亮度、梯度和边缘信息进行Census变换和Hamming距离计算,将三者的计算结果融合,构建新的代价计算函数。与传统SGM算法相比,所提算法不仅提高了视差计算效率,而且改善了重复纹理、弱纹理及边缘区域的视差结果,提高了视差计算精度。

1 基于特征点的视差范围估计

针对传统SGM算法对视差范围未知场景，通常人为确定一个视差范围,造成计算资源浪费的不足,提出了一种基于特征点的视差范围估计方法。该方法的核心在于统计左右图像中特征点对的有效视差来估计整个图像的视差范围,进而达到快速、可靠估计视差范围的目的。

1.1 特征点的提取和匹配

目前,常见的特征点算法有:尺度不变特征变换(scale-invariant feature transform,SIFT)、SURF、加速分割测试获得特征(features from accelerated segment test,FAST)、BRISK以及ORB等。其中,SIFT是一种非常稳定的局部特征,但本身计算过程过于复杂,实时性不高;SURF是SIFT的加速版,核心在于采用了Hessian矩阵和盒子滤波器等概念,比SIFT更快更具有鲁棒性;FAST检测速度快,可应用在实时场景中,但容易受到噪声的影响,鲁棒性较差;BRISK检测速度快,具有较好的鲁棒性;ORB运行时间远低于SIFT和SURF,可用于实时的特征检测。

为了使特征点对的视差值能更全面地表征图像的视差范围,提高视差范围估计的可靠性,需要尽可能多地提取图像的特征点。因此,首先联合几种运行速度较快且鲁棒性较好的SURF、BRISK、ORB算子同时检测图像对的特征点;然后对所有特征点统一采用鲁棒性最好的SURF描述子计算特征向量;最后通过FLANN方法进行特征点匹配,获得初始的特征匹配结果。待匹配图像对锥面如图1所示,初始匹配结果如图2所示,一共生成了4 995对匹配点对,但存在大量明显错误的匹配点对。

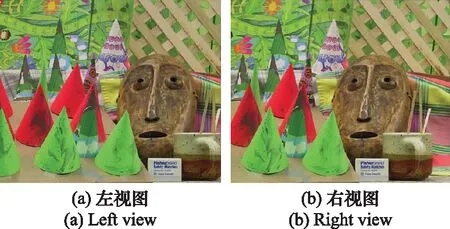
图1 立体图像对锥面Fig.1 Stereoscopic image pair cones

图2 初始匹配结果Fig.2 Initial match result

1.2 剔除错误的匹配点对

为了减小错误的匹配点对对视差范围估计的影响,提高视差范围估计的可靠性,利用立体匹配的约束条件对匹配点进行筛选。常见的立体匹配约束准则有以下几点。

(1) 极线约束:将左右图像的极线对齐,使得匹配点对在同一水平线上,匹配点对应该具有相同的纵坐标。

(2) 相似性约束:匹配点对应该具有相似的灰度值和梯度值。

(3) 视差范围约束:沿着极线方向搜索匹配点时,搜索的范围受到最大视差值的约束。

综合上述约束条件对匹配点进行筛选,满足条件保留,不满足条件剔除。假设、分别是左右图像中对应的特征点,总的约束条件为

(1)

式中:(·)、(·)分别表示特征点对应的灰度值和梯度值;、分别表示特征点的横纵坐标;、、分别表示匹配点对对于灰度值、梯度值和纵坐标设定的允许波动的截断值;表示人为设定的视差最大值。

筛选后的匹配结果如图3所示,此时还有1 053对匹配点对,剔除了大量错误的匹配点对,匹配点对都保持在同一极线上。

图3 筛选后的匹配结果Fig.3 Filtered matching results

1.3 视差范围估计

根据筛选后的特征匹配结果计算视差,估计图像的视差范围。虽然通过约束条件剔除了大量的误匹配点,但匹配结果中仍存在异常值。多次实验结果表明,为了增强视差范围估计的鲁棒性,对匹配点对计算视差后,舍去其中的最大和最小视差值,选择次最大和次最小视差值分别作为视差范围的上下边界。为了进一步增强鲁棒性,还应对次最大和次最小视差值进行一定补偿,作为最终视差范围的上下边界。表1为锥面的视差估计范围和真实范围对比。

表1 视差范围对比

2 改进的代价计算

2.1 传统的Census变换

传统SGM算法通常采用Census变换进行匹配代价计算。传统Census变换将中心像素及其邻域内像素亮度的相对大小关系转换为比特串,作为中心像素的Census变换值:

(2)

(3)

式中:⊗表示按位连接,选取中心像素(,)周围大小为×的窗口,′=|2|,′=|2|;(·)表示图像像素的亮度。

计算左右图像Census变换值Cen和Cen的Hamming距离作为中心像素的初始匹配代价:

(,,)=
Hm[Cen(,),Cen(-,)]

(4)

2.2改进的代价计算

传统Census变换进行匹配代价计算时仅考虑了图像的亮度信息,在重复纹理区域易导致误匹配。弱纹理区域主要通过边缘信息进行匹配,匹配时过于依赖边缘阈值,而且在复杂的背景环境下确定有效的边缘阈值并不容易。为了提高重复纹理和弱纹理区域的匹配精度,分别对图像的亮度、梯度和边缘信息进行Census变换和Hamming距离计算,将三者计算结果融合,构建新的代价计算函数。

图像的梯度是一个用来衡量图像水平和垂直方向上灰度变化率的二维向量,即:

(5)

数字图像本质上是一个二维离散函数,一般使用灰度差分近似对图像求导,则图像在(,)处的水平和垂直方向的梯度值分别通过中值差分表示为

(6)

式中:(,)为图像在(,)处的灰度值。

结合水平和垂直方向的梯度值,得到图像的梯度信息:

(7)

图像的边缘是图像中两个区域的交接处,通常是局部亮度或结构发生急剧变化的地方。Sobel是一种典型的边缘检测算子,一般利用水平和垂直方向上的两个简单的3×3内核,如图4所示,与图像进行卷积操作得到图像梯度的近似值,通过判断梯度值与边缘阈值的大小关系获取图像的边缘信息。

图4 Sobel算子Fig.4 Sobel operator

得到图像的亮度、梯度和边缘信息后,引入估计好的视差范围,分别对它们进行Census变换、Hamming距离计算,则像素点(,)在视差下,基于图像边缘和基于图像梯度的匹配代价分别表示为

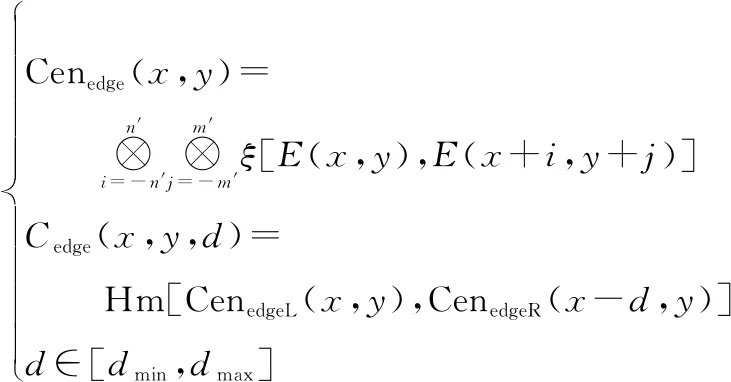
(8)

(9)

式中:(·)、(·)分别表示图像的边缘值和梯度值;Cen(·)、Cen(·)分别表示基于边缘和基于梯度的Census变换值,(·)、(·)分别表示基于边缘和基于梯度的匹配代价;[,]为事先估计好的视差范围。

将分别基于图像边缘、亮度和梯度的匹配代价融合,构建新的代价计算函数:

∈[,]

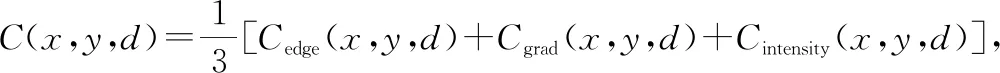
(10)

对于重复纹理区域,改进的代价计算在Census变换的基础上,综合考虑了邻域内图像的亮度、梯度和边缘信息对匹配的影响;对于弱纹理区域,改进的代价计算对边缘信息进行Census变换,匹配时将不再关注于边缘的具体取值,而在于邻域内边缘的相对大小关系,削弱了边缘阈值对于匹配的影响,进而有效地改善了重复纹理以及弱纹理区域的匹配效果。

3 实验结果与分析

将经过立体校正的图像对作为本文算法的输入,首先利用基于特征点的视差范围估计方法估计出图像的视差范围,然后将估计的视差范围引入传统SGM算法中,依次进行改进的代价计算、代价聚合、视差计算及视差优化。传统SGM算法和本文算法的流程图对比如图5所示。

本文采用Middlebury立体匹配测评网站提供的4幅标准图像对筑波、金星、泰迪、锥面进行实验,涉及实验参数的设置如表2所示。实验环境在CPU为Intel core i5 1.80 GHz, 操作系统为Windows 10的个人电脑上的Visual Studio 2019下,配合图像处理开源库OpenCV 3.2.0。

图5 不同算法的流程图Fig.5 Diagram of different methods

表2 实验参数设置

为了验证所提算法的性能,选取了传统SGM算法进行实验对比,如图6所示,从左到右依次为图像对的左图、真实视差图以及传统算法和所提算法生成的视差图。首先对传统SGM算法和所提算法进行定性分析。本文用白色方框框出了视差图的部分区域,如图6(c)和图6(d)所示。相比传统算法,对于筑波和金星,本文算法在白色方框区域上的物体边缘更清晰,轮廓曲线更平滑,更接近真实视差图,说明所提算法有效改善了深度不连续区域的匹配效果;对于具有复杂场景的泰迪,所提算法在白色方框区域上视差计算结果更为精确,说明所提算法有效改善了边缘遮挡区域的视差精度;对于同样具有复杂背景的锥面,在具有重复纹理的三角圆锥区域,所提算法也成功匹配出了各个圆锥,说明所提算法有效改善了弱纹理及重复纹理区域的视差精度。然后对传统SGM算法与本文算法进行了定量分析。从3个区域非遮挡区域(non)、所有区域(all)以及深度不连续区域(disc)分别来验证算法的鲁棒性。将算法生成的视差图与真实视差图进行比较,相差结果大于误差阈值(本文设定阈值为1)的像素被视为误匹配。这两种算法在测试图像对上的误匹配率如表3所示,运行时间如表4所列,实验结果表明,本文算法在这4幅图像对上所有区域的误匹配率均低于传统算法,平均误匹配率为7.65%,相比传统算法降低了6.38%,在提高整体匹配精度的同时,本文算法还将每幅图像对的计算时间缩短了95%以上,匹配时间均不超过2 s,实现了快速的立体匹配。

对于所有图像对,特征点对数量与处理时间如表5所示,基于特征点估计的视差范围和真实范围对比如表6所示,虽然估计的视差范围与真实范围还是存在一定的偏差,但正是由于本文通过特征点检测的方式缩小视差的搜索范围,提高算法的计算效率,而且特征处理时间仅占据整个算法运行时间的20%左右,从而将算法的运行时间缩短了95%以上,保证了快速的立体匹配。此外,本文还采用了综合考虑图像的亮度、边缘和梯度信息的Census变换计算匹配代价,从图6可以看出在重复纹理、弱纹理及边缘区域的视差结果均得到了显著改善,在保证计算效率的同时本文又进一步提升了视差精度,实验数据也验证了本文匹配代价的有效性,由表3可以看出相比传统算法,本文方法在non、all以及disc区域的视差精度均有不同程度的提升。

图6 不同算法生成的视差图Fig.6 Disparity maps generated by different algorithms

表3 两种算法的误匹配率

表4 不同算法的运行时间

为了进一步客观分析所提算法的性能,还选取了Middlebury网站上一些实时及接近实时的立体匹配算法进行比较,不同算法的误匹配率如表7所示。对于筑波和金星这样视差范围较小的简单图像对,所提算法的误匹配率接近表中的最优算法,侧面反映了所提算法在简单纹理图像中具有较好的视差估计能力。对于泰迪和锥面这样视差范围较大的具有复杂场景的图像对,本文算法的平均误匹配率由小到大分别位于第二和第一,且在泰迪上仅比第一低0.1%,匹配精度较高,这说明视差范围越大、图像的场景越复杂,所提算法的性能也越强。除此之外,所提算法在所有图像对上的平均误匹配率为7.65%,在上述算法中最低,说明本文方法具有较强的鲁棒性,受场景纹理的影响较小,能较好的适用于各种不同的场景。综合立体匹配的速度和精度考虑,本文算法具有很高的实际应用价值。

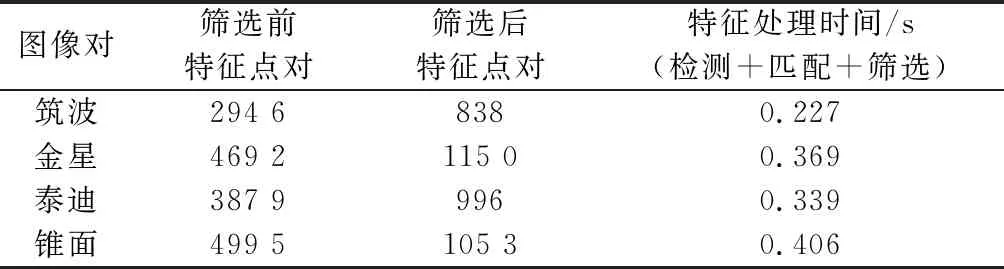
表5 不同图像的特征点对数量与处理时间

表6 视差范围

表7 不同算法的误匹配率

4 结 论

本文改进了传统SGM算法,提出了一种基于特征点的视差范围估计方法,提高了视差计算效率;构建了新的代价计算函数,改善了重复纹理、弱纹理及边缘区域的匹配效果。实验结果表明,与传统SGM算法相比,本文算法的平均误匹配率降低了6.37%,计算时间缩短了95%以上,与其他实时性及近实时算法相比,本文算法具有较强的鲁棒性,能较好地适用于各种不同场景。