浅析初中数学说题模式

王发生

中图分类号：A 文献标识码：A

随着课程改革的层层深入、“双减”政策的不断推进，各地区不断涌现出初中数学说题的热潮。这也促进了教师对教材、对题型越来越重视，不断对学生作业设计和中考题型的探究和思考。

那么，就说题而言，什么样的流程或模式是较为科学和实用的呢？这就像教法一样，教无定法，同样，说题也没有固定的流程模式，视具体情况而定，看怎样的流程或模式适合题型、适合自己。近几年来，各地区举行的说题模式也是各有千秋，百花齐放。

一、说题模式多种多样

如模式1.（1）说题背景、（2）原题再现、（3）阐述题意、（4）思路策略、（5）变式拓展、（6）教学反思、（7）总结提炼。模式2.（1）原题再现、（2）题目分析、（3）一题多解、（4）一题多变、（5）拓展延伸。模式3.（1）原题呈现、（2）背景分析、（3）回归课本、（4）问题解决、（5）拓展探究、（6）课后反思。模式4.（1）题目再现、（2）命题意图、（3）考查目标、（4）教学思想、（5）解题思路、（6）题目变式、（7）课后反思。模式5.（1）题目展示、（2）命题意图、（3）试题解答分析、（4）试题变式与拓展、（5）解题方法小结。

二、我的说题模式

（一）、题意与思路

1.（1）原题再现与知识回顾：如图，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合.三角板的一边交CD于点F，另一边交CB的延长线于点G.求证：EF=EG;

1）三角板与正方形的性质是什么？

2）全等三角形和相似三角形的判定与性质有哪些？

2.条件关系与基本背景：

（1）已知正方形ABCD，∠GEF=90°，都是原题的

已知条件。（2）正方形的各边都相等、角为90°， ∠BEF为两直角的公共角，是图形中隐含条件。

1、题材背景：新人教版2016年山东青岛中考21题;2、知识背景： ①正方形、矩形的性质;②全等三角形的判定与性质;③相似三角形的判定与性质;④平移的应用;3、 思想背景：转化思想、数形结合思想、类比思想。

3.思路形成与条件路径：

本题以能力立意，考查学生灵活运用所学知识解决问题的能力，近年的中考数学试题中，有关三角形、四边形构成的几何综合题占据相当的比例，利用类比思想去解决动点问题，充分体现了解题能力和提高素质教育的思想和要求，这也是《新课程标准》的要求。条件路径1.证明线段相等的方法有哪些？2.如何证明线段EF=EG呢？

4.解题思路与关键突破：

思路：（1）把EG、EF分别看做△EGB和△EFD的边。（2）只需证明△EGB≌△EFD（ASA），可得 EF = EG。

关键突破：（1）能不能从图形中提取隐含条件，获取有效的信息。（2）发挥空间想象，是否能想到用全等的方法去说明这两条线段相等。（3）探究和发现平移的性质与全等三角形，相似三角形的判定的联系，把动点题型转化成定点题型去解答。

（二）、思想及推广

1.主要技巧及作用：

在本题的教学过程中，我们主要引导学生，一是对题意全方位、多角度的分析、理解，二是要证明这两条线段相等要通过三角形的全等，要充分联想回忆基本知识，三是要寻求三角形全等的条件，特别是挖掘题意中的隐含条件。

2.教学思想及方法：

在本题的教学过程中，我们要用到分析法、综合法、类比法。用分析法时可以从结论向已知追溯，推求它成立的充分条件。

3.数学思维及过程：

在本题的教学过程中数学思维过程，是指从理解正方形ABCD，三角形直角顶点放在顶点A处，另两边与正方形相交题意开始，经过探索∆FED和∆GEB全等的思路，转换成两个三角形全等的性质EF=EG来解决问题。其实这个过程可以用理解、转换、实施、验证加以概括。

4.推广类型及变式拓展：

推广类型一

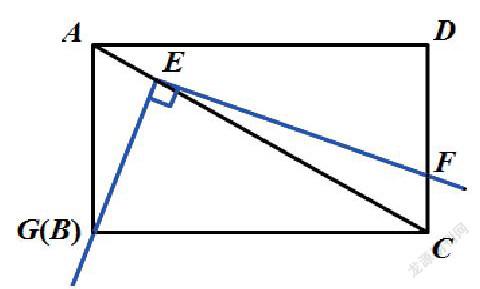
（2）如图，移动三角板，使顶点E 始终在正方形ABCD的对角线AC上，其他条件不变，原题中的结论是否仍然成立？若成立，请给予证明;若不成立，请说明理由;

推广类型二

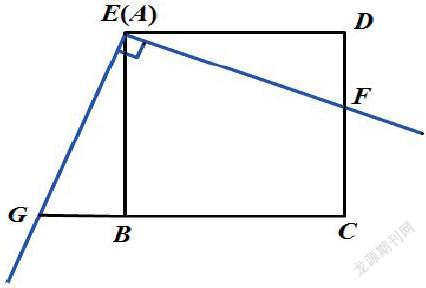
（3）如图，将（2）中的“正方形ABCD”改为“矩形ABCD”，且使三角板的一边经过点B，其他条件不变，若AB=a，BC=b，请直接写出EF：EG的值.

变式拓展一

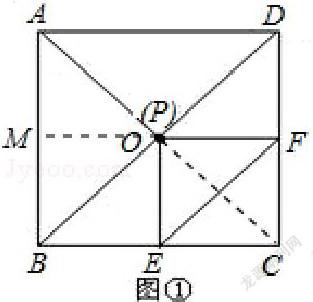
在正方形ABCD中，点O是对角线DB的中点，点P是DB所在直线上的一 个动点，PE⊥BC于E，PF⊥DC于F.

（1）当点P与点O重合时（如图①），猜测AP与EF的数量及位置关系，并证明你的结论;

中考联系：以上推广类型、变式拓展的条件或问题，虽然在原题的本质结构上有所变化，但利用类比法构造全等三角形或相似三角形并证明的解题思路不变，本题的原型取材于中考试题。

（三）、价值和技能

1.实践意义：教学中一定要让学生在相互交流的实践活动中各抒己见，互献智慧，在磨练中探索、尝试、验证，进行思想方法的沟通，以达到集思广益和突破创新的目的，能培养学生思维的深刻性、广阔性、创造性乃至批判性，开发学生的脑力资源，挖掘学生的潜在能力。

2.教材内容

本题涉及到的教材内容在整个初中几何内容中交叉排版，又呈螺旋上升的方式，由简单到复杂、由低层到高层，不断深化，综合发展，符合中学生思维发展特点，及学习教学的心理规律和需要。

命题联系：本题在本质结构上的原型解答还是较为简单的，在推广类型上稍提加了一点难度，在实际问题的解答中需要添加辅助线，构建全等三角形才能解答;在变式拓展中又在推广的基础上增加了难度。

3.数学思想

本题体现了数学中常见的转化思想、类比思想和数形结合思想。教法设计：1、注重师生平等关系，体现教师是学生的组织者、引导者、合作者，学生是学习的主人。2、能恰当合理运用现代教育技术。

4.课后反思

（1）本题考查的知识点较单一，从形的角度分析较直观，但如何利用类比法作辅助线也是难点。所以，我们首先设置问题，引发学生思考并发现隐含的条件，最后通过作輔助线构造三角形全等和三角形相似，继而得出结论，很好的突破难点。

（2）本题的几个变式由浅入深，起点高，落点低，对学生的理解能力和应用能力有较高的要求，虽然综合理解性较强，但是通过类比的数学思想，相信学生能够灵活运用所学知识解决问题。

5.突破创新：我们深知，在初中数学教学中，提高由简单到较为复杂的几何命题的解答正确性、成功率，这都成为教育教学研究的重点，成为提高教学效益的研究核心。基于这种认识和思考，我们要不断突破，提升我们教师对教学、对学生作业设计、对中考命题的一些思考和探究。