基于粒子收敛机制的WSN覆盖算法
2022-02-22叶小华
叶小华
(黎明职业大学 通识教育学院,福建 泉州 362000)
无线传感网技术(Wireless Sensor Network,WSN)作为供给侧改革重点方向之一,正在新一代智慧城市构建领域中发挥举足轻重的作用[1].由于无线传感网采用自组织方式将传感器部署于物理区域,可通过无线感知模式实现对物理区域的监控,因而在绿色农业、智慧通信和新冠防疫等领域具有广泛用途[2].考虑到无线传感节点部署密度较高,节点通信频率较为频繁,因此如何采取一定措施提高网络及节点覆盖能力并增强网络生存质量,成为当前热门研究领域之一[3].
WSN覆盖技术主要立足于节点部署策略、能量利用效率及覆盖强度等方面,其中覆盖强度主要反映了网络对物理区域的感知能力[4].以绿色农业为例,WSN覆盖主要存在三个方面.第一,节点在物理区域内采用随机游走模型,使得分布具有聚类特性,导致感知能力难以均衡.第二,网络结构较为复杂,簇头节点处于受限状态时将导致网络传输出现瘫痪现象.第三,节点通信较为频繁,采用无线充电模式将导致严重的电磁频谱污染现象,降低网络生存质量[5].因此,为降低能量及传输受限时可能出现的覆盖能力下降现象,需要尽量节约能量的前提下提高节点覆盖效率,以便能够改善网络生存质量.
当前,研究者提出了一些具有前瞻性的研究方向,在一定程度上提高了节点覆盖效率.如Susila[6]等提出了一种基于休眠切换方案的WSN覆盖算法,算法主要采用预部署模型,在物理区域内均匀部署若干簇头节点以增强网络覆盖能力,可显著降低节点受限时出现的传输受阻现象,网络生存质量较高.不过,该算法也存在预部署节点数目过多的特点,使得网络节点切换过程易出现失效现象,网络覆盖能力也将受到严重影响.Kumar[7]等提出了一种基于移动拨备模型的WSN覆盖算法,该算法与文献[6]相比,创造性地采用移动模型对节点进行预部署,可显著增强节点覆盖强度,且具有充能方便的特点.不过,该算法也存在一定的不足,特别是节点是移动状态时存在频率漂移特性,使得网络结构易出现抖动现象,降低了该算法的适用性能.Thiruchelvi[8]等提出了一种基于栅栏覆盖模型的WSN覆盖算法,该算法采用条状分割模型将节点进行层次化处理,优选具有较强覆盖能力的节点作为层次覆盖节点,显著提升了网络对物理区域的感知能力,节点覆盖能力较强.不过,该算法需要频繁针对物理区域进行层次覆盖流程,使得算法的便捷性较差,难以适应大规模部署场景.
为解决当前常见方案存在的不足,提出了一种基于粒子收敛机制的WSN覆盖算法.算法主要采用定位校正方式对预设锚节点进行均衡操作,当察觉存在聚集现象时将予以离散处理,从而提高了网络区域覆盖能力.随后,按照多参数方式设计了基于惯性权重调节机制的聚合收敛方法,改善了覆盖空洞现象,提高了网络生存质量.仿真实验证明了所提算法的性能.
1 基于粒子收敛机制的WSN覆盖算法
由于无线传感网具有节点分布较为密集的特点,使得节点感知易出现失效现象,需要通过密集模式提高节点覆盖能力[9].鉴于此,本文算法由两个部分构成,基于均衡锚预设机制的收敛覆盖方法和基于惯性权重调节机制的聚合收敛方法.
1.1 基于均衡锚节预设机制的收敛覆盖模型
典型的无线传感网覆盖模型见图1.网络区域内分布若干锚节点和子节点,两类节点均可通过无线通信方式实现数据交互.当且仅当子节点处于锚节点覆盖范围内时,方可将数据传输至锚节点并通过锚节点实现与sink节点间的数据交互传输.此外,无线传感网在运行过程中遵循如下假设条件.
(i)sink节点具有超级节点属性.sink节点在网络覆盖过程中具有最高优先级,可对锚节点和子节点实施管理,若发现锚节点和子节点处于失效状态时,可予以剔除.
(ii)节点能量可补充.锚节点与子节点处于受限状态时,可进入休眠状态并由sink节点予以能量补充,一旦能量得到恢复可继续进行数据监测和网络覆盖.
(iii)数据传输具有一跳特性.锚节点和子节点均只能与自身覆盖范围内节点进行通信,数据传输至sink节点过程中需要采取数据中继的方式,以便与sink节点实现双向交互.
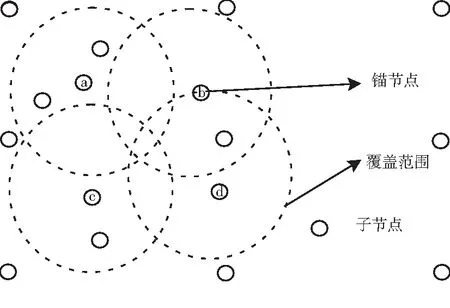
图1 网络覆盖图
将网络中剩余能量较高的节点设定为锚节点(Anchor Nodes,AN节点),锚节点的物理坐标可依据WSN节点定位算法获取[10].不妨设当前AN节点的坐标为X(x,y),其偏移量为ΔX(x,y),成功获取坐标和偏移量后,按如下模型进行均衡收敛.
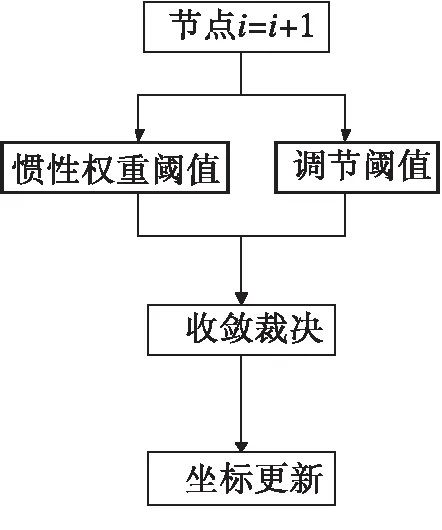
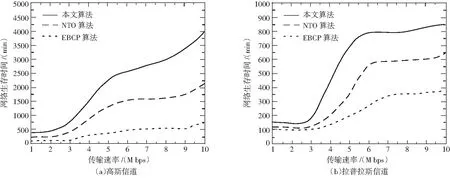
ΔX(x,y)[m+1]=X(x,y)[m],ΔX(x,y)[m] (1) ΔX(x,y)[m+1]=ΔX(x,y)[m],ΔX(x,y)[m]≥D[m+1], (2) 公式(1)和(2)中,m表示坐标定位次数,X(x,y)[m]表示第m次定位过程中AN节点的坐标,ΔX(x,y)[m]表示第m次定位过程中AN节点坐标的偏移量,D[m]表示收敛覆盖函数,该收敛覆盖函数可通过如下方式获取. D[m]=min{D[k],D[k-1],…}, (3) D[1]=ΔX(x,y), (4) 公式(3)中D[m]取{D[k],D[k-1],…,D[1]}中的最小值,公式(3)和公式(4)中参数同公式(1)和公式(2). 考虑到收敛覆盖过程中需要引入中断,这是由于覆盖过程中可能存在能力受限现象,从而使得锚节点难以实现区域覆盖功能.鉴于此,本文设计了覆盖收敛聚合度(Convergence Degree of Coverage,CDC)和覆盖发散度(Coverage Divergence,CD)指标,对公式(1)和公式(2)所示的均衡收敛模型予以约束,相关指标可由如下公式获取. (5) (6) 当CDC趋向于m时,说明在第m次定位过程中各锚节点分布较为均衡,无须继续进行收敛即可完成物理区域的覆盖,当CD趋向于0时,说明第m次定位过程中各锚节点分布较为稀疏,需要进行收敛以便完成对物理区域的覆盖,见图2. 图2 基于均衡锚节预设机制的收敛覆盖过程 按上图2所示完成基于均衡锚节预设机制的收敛覆盖方法后,锚节点将被均匀地预设于网络区域中,一旦某个区域出现覆盖空洞现象,将可以通过裁决CD值的方式继续对锚节点予以均衡化覆盖,从而提高锚节点对物理区域的覆盖强度. 基于均衡锚节点预设机制的收敛覆盖方法执行完毕后,预设的锚节点将能按照较高的乖离程度以实现均衡部署.然而,考虑到节点具有的漂移特性,需进一步对锚节点予以聚合收敛处理,以便提高锚节点的覆盖能力. 步骤1 针对网络中的锚节点,逐个按如下模型获取惯性权重阈值f(x,y)[m]. (7) 公式(7)中,(x,y)表示锚节点的当前坐标,(x0,y0)表示锚节点的初始坐标,g表示锚节点的通信距离. 步骤2 获取惯性权重阈值f(x,y)[m]后,构建调节阈值o[m]如下. o[m]=f(x,y)[m]-f(x,y)[m-1] , (8) 公式(8)与式(7)中参数相同. 步骤3 当且仅当调节阈值o[m]高于0时,说明锚节点在第m次定位过程中可继续进行收敛,收敛方法如下. o[m]>0,L[m], (9) o[m]<0,L[m-1] , (10) 其中,L表示位移,L[m]满足 L[m]=ΔX(x,y). (11) 步骤4 继续针对下一个锚节点获取惯性权重系数并回退至步骤1,流程结束. 图3 基于惯性权重调节机制的聚合收敛过程 基于惯性权重调节机制的聚合收敛方法执行完毕后,锚节点可达到较强的覆盖效果,且节点与各传感节点间将具有均衡化的分布距离,节点乖离程度也将处于较高水平,此时网络覆盖将达到最优状态. 为对比所提算法性能,采取NS2仿真实验平台[11].对照组算法为当前无线传感网覆盖领域中常见的基于拓扑优化覆盖策略的WSN覆盖算法[12](A Novel Topology Optimization of Coverage-Oriented Strategy For Wireless Sensor Networks,NTO算法)和基于能量平衡和参数受控机制的WSN覆盖算法[13](Data Association Coverage Algorithm Based on Energy Balance and Controlled Parameters in Wireless Sensor Networks,EBCP算法).仿真指标选取网络覆盖率和网络生存时间两项. (i)网络覆盖率指节点开始工作后,随着工作节点总数的变化,能有效覆盖目标节点中工作节点监测区域与网络覆盖总区域面积的比值.若平均覆盖率越高,说明节点覆盖性能也就越好,网络覆盖性能也就越高. (ii)网络生存时间指网络开始工作后直到网络无法工作为止,网络经历的时间周期.若时间周期越久,说明网络的生存性能也就越好. 此外,考虑到仿真环境与实际环境的贴合性,仿真区域为矩形,大小为10240 m×10240 m,仿真时间不低于10 min,数据速率不低于1 Mbps,锚节点数量不低于20个,数据传输周期不低于24 min,信道环境采取拉普拉斯信道和高斯信道两种环境,其余仿真参数见表1. 表1 仿真参数表 图4为所提算法、NTO算法和EBCP算法在网络覆盖率方面的对比仿真,由图4可知所提算法在拉普拉斯信道和高斯信道两种环境下均具有较高的网络覆盖率,显示了优越的网络覆盖性能.这是由于所提算法针对网络覆盖空洞问题,设计了基于均衡锚预设机制的收敛覆盖方法和基于惯性权重调节机制的聚合收敛方法.可通过锚节点方式对网络区域实现多重覆盖,并可通过均衡锚预设方式调节锚节点的均衡覆盖水平,因而具有较高的网络覆盖率.NTO算法主要采用均等概率机制定期更新网络区域簇头节点,将无线传感器网络的整体能耗均匀分布到传感器节点上,实现簇内成员节点数据的均衡分布,从而提高节点的拓扑覆盖质量.但是,由于该算法未采用轮询机制对簇头节点进行更新操作,簇头节点失效率较高,降低了算法的网络覆盖能力,因而网络覆盖率要低于所提算法.EBCP算法采用了簇内低功耗和簇间高功耗的分簇思想,结合信道分配减少节点覆盖时延,实现了簇间无冲突覆盖,从而改善了网络覆盖性能.但是,由于该算法存在分簇均衡程度较低的特点,使得簇头节点对区域覆盖能力较低,因而该算法的网络覆盖率亦要低于所提算法. 图4 网络覆盖率 图5为所提算法、NTO算法和EBCP算法在拉普拉斯信道和高斯信道两种环境下的网络生存时间测试结果.由图5可知,所提算法具有网络生成时间较高的特点,显示了优越的网络生存性能.这是由于所提算法针对网络节点能耗所导致的覆盖问题,设计了基于均衡锚预设机制的收敛覆盖方法,以提高簇头节点的覆盖性能,特别是所提算法考虑到节点受限出现的覆盖空洞现象,设计了基于惯性权重调节机制的聚合收敛方法,可提高锚节点对传感区域的覆盖能力,降低了因能量受限而导致的覆盖空洞现象,因而网络生存质量较高,具有较长的网络生存时间.NTO算法采用均衡概率模型以提高簇头节点覆盖能力,但并未采用备份机制及时更新簇头节点,因而网络覆盖率较低,易出现明显的网络受限现象,使得网络生存时间要低于所提算法.EBCP算法为提高网络生存质量,结合信道分配减少节点覆盖时延,实现了簇间无冲突覆盖.但是,该算法所选的簇头均衡化水平较低,使得节点覆盖性能较差进而导致节点分布较为集中,加剧了网络拥塞现象,因而网络生存时间要低于所提算法. 图5 网络生存时间 为提高无线传感网的均衡覆盖能力,提出了一种基于粒子收敛机制的WSN覆盖算法,算法主要由基于均衡锚预设机制的收敛覆盖方法和基于惯性权重调节机制的聚合收敛方法两部分构成,可显著提高网络覆盖能力,具有锚节点分布均衡程度较高的特点,网络覆盖性能优越.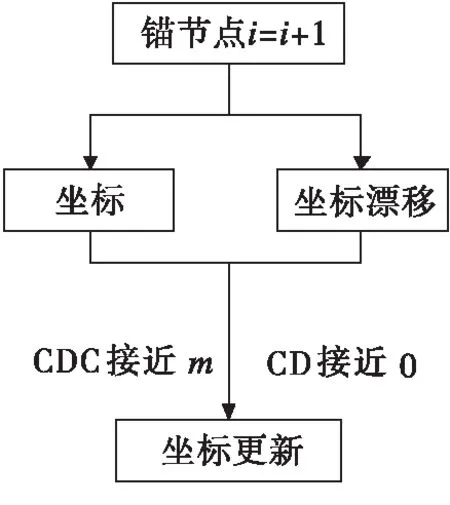
1.2 基于惯性权重调节机制的聚合收敛
2 仿真实验

2.1 网络覆盖率
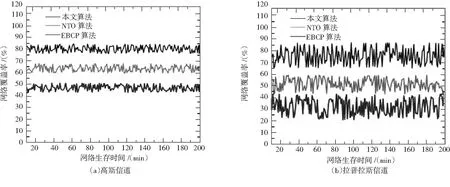
2.2 网络生存时间
3 结束语
