以平均数的教学为例谈“变教为学”
2022-02-22山东菏泽市定陶区张湾镇沙山寺小学274104董金宪
山东菏泽市定陶区张湾镇沙山寺小学(274104)董金宪
平均数属于统计与概率这一大分支,如果教学时教师拘泥于平均数的计算公式,只追求顺利计算出平均数,忽视对平均数本源和用途的考究,那么学生在计算平均数时就会犯下各种低级的错误,即使他们明明对平均数的计算公式烂熟于心,但是由于弄不清算理,还是会错误频出,有时错了还不知道自己错在哪里。能熟练运用平均数的计算公式,并不代表对平均数的算理融会贯通了,也不意味着对平均数的概念心领神会。下面笔者以教学“平均数”为例,来说明如何设计活动记录单。
一、追溯历史,正视平均数
通过对平均数起源的考证,可以发现,平均数是用来估计大数的。在一个印度神话故事中,有一棵参天大树长有茂盛的枝叶,树枝粗细各异。故事的主人公出于好奇,想计算出每根树枝上的叶片数,他想了想,先数出靠近树根的一根纤细树枝上的叶片数,再乘以大树树枝的数量,得结果为2095,第二天人们齐心协力数了一下,得出的结果和这个主人公估算的结果差不多。尽管这个神话故事中没有交代清楚主人公如何选择的树枝,但是,可以肯定的是,他必须选择一根中等粗细的树枝,这样估算的结果才不离谱。这选择树枝的过程和标准就代表着平均数的思想,因为所选的树枝必须具有代表性,既不能过于粗大,又不能过于纤细,这样,在求总数的过程中,它才能有效平衡各种树枝,起到一个调剂中和的作用,移多补少。
这个与平均数有关的神话给我们带来启发,平均数的学习应该从估算大数起步,因此,笔者设计了活动一,通过活动一让学生理解平均数可以代表一组数据的整体水平。
【活动一】某手机代工企业总共有30间厂房,每间厂房的员工人数分别为42,35,36,43,40,58,
47,34,39,50,37,42,47,34,39,45,50,48,52,49,47,32,36,45,35,46,47,38,51,46,你能算出该企业一共有多少员工吗?和同学交流一下你的想法。
活动一要求学生算出代工企业共有多少员工,也就是让学生对这组数据进行求和,这种操作和数树叶有着异曲同工之处。由于估算方法本身就是多样的,再加上学生的个体差异和创新力,因此,学生会冒出许多不同的解法。
方法一:将这组数据中的两个最值(最大值和最小值)相加,再平均分成2份,求出两个数的“中间值”,然后用这个“中间值”代替组内每个数据,用这个数乘以30。
方法二:将这组数据重新排列,按照从大到小的顺序排列,然后找到处于正中间位置的那个数,再假设每个数都是这个中位数,用这个数乘以30。
方法三:一一查点,看哪个数出现的频次最高,也就是找出重复出现次数最多的那个数,假设每个数都是这个数,再用这个数乘以30。
方法四:运用“四舍五入”法将每个数据看成整十数,如将“42”看作“40”,将“47”看作“50”,将“34”看作“30”……再求出总和。
前三种方法都是选取一个代表整体水平的数值再算总数,这样能较为科学准确地算出总数,才能有效地估算大数。虽然有的厂房的员工人数会多于或少于这个选定的数,但是在求和的时候,会互相抵消。活动中,学生通过自行摸索和创新也生成了统计与概率中的中位数、众数的前概念。通过这个活动可以发现,平均数和估算有着千丝万缕的关系,并且学生通过独立思考后提出的平均数、中位数和众数等形式很有说服力,将学习内容与数学知识紧紧捆绑在一起。教师不妨在开展完活动一后趁热打铁讲述这个印度神话故事,让学生深思平均数的内涵。
任何数学概念的产生都有原因,平均数也不例外。其实计算平均数是简单的,只需要将各个数据相加,然后除以数据个数即可,一旦数据较多,这样计算就非常烦琐,而且在学生眼里,平均数又没有什么实际用处,因此不愿意学。小学低年级阶段,学生接触的都是具体运算,没有接触过抽象的统计,平均数其实是一个统计数据,为了让学生更好地接受平均数,并且自觉运用,介绍平均数的来由就显得十分重要。平均数的功能就蕴含在平均数的来历中,因此,要实现“变教为学”,就要学生自主探究,自己去发现平均数的用途和优势,例如,让学生计算工厂员工总数,如果估算好平均数,那么计算就会十分方便,学生在多方探究中自己发现平均数的优势。
二、学会计算,领悟功能
【活动二】(1)人们可以在甲、乙两个乡镇卫生院接种新冠疫苗,表1列出了甲乡镇卫生院四周接种新冠疫苗的人次,表2列出了乙乡镇卫生院三周接种新冠疫苗的人次,你知道哪个乡镇卫生院的周业务量较高吗?(2)乙乡镇卫生院在第四周接种新冠疫苗的人次是多少,才能使该卫生院平均每周接种新冠疫苗是70人次?和同伴交流一下你是怎么计算的。
本次亲土状元选拔赛,是今年该系列大赛的收官之作,吸引了300多名来自洛川各乡镇的苹果种植能手。他们当中,既有像杨华鹏一样子承父业的“果二代”,也有自费到日本学习果树管理的“技术控”,以及在电商平台逐渐做强品牌的“网红果王”。大家一早便带着自己的得意之作来到大赛现场,个个摩拳擦掌,对亲土状元志在必得。
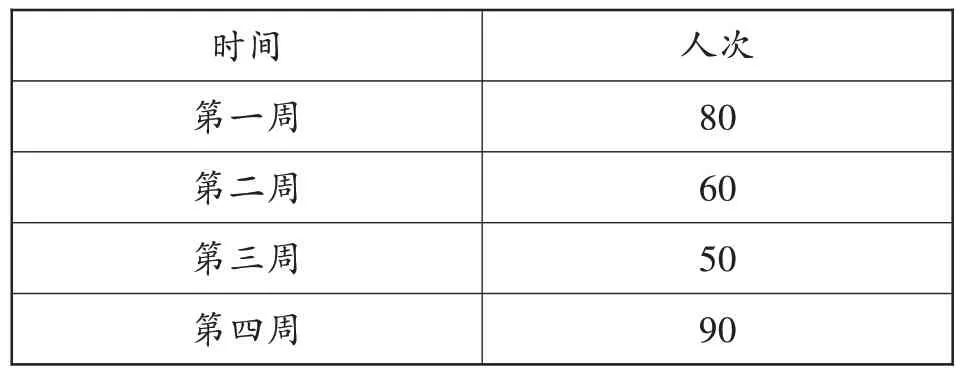
表1 甲乡镇卫生院四周接种新冠疫苗的人次
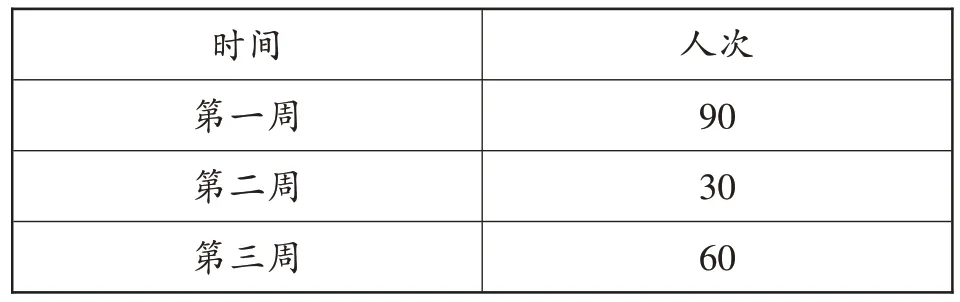
表2 乙乡镇卫生院三周接种新冠疫苗的人次
活动二的第(1)问,第一个目的在于让学生学习并掌握平均数的两种基本算法,一种是先将所有数据加起来,再除以数据个数,另一种则是移多补少;第二个目的在于向学生传递信号——平均数可以代表一组数的整体水平和另一组数做比较,让学生体会到平均数的对比功能。学生经过研究和思考就会发现,此时用接种新冠疫苗的总人次比较两个卫生院的业务量不公平,也不科学,因此会想出如下方法。
方法一:分别算出甲、乙两个乡镇卫生院接种新冠疫苗的总人次,再除以对应的周数,就可以得出每个卫生院每周接种人次,也就是周业务量。
方法二:把甲乡镇卫生院第一周的10人次转移到第二周,把第四周的20人次转移到第三周,此时每周接种人次相等。把乙乡镇卫生院第一周的30人次转移到第二周,此时每周的接种人次也会相等。最后用两个数进行比较。
活动二的第(2)问是这样设计的,已知四个数据的平均数和它们中的三个数据,据此推算第四个数据。这是通过已知平均数逆向求解未知数据,这种逆向出题思路,考查的就是学生对平均数的通盘考虑能力。学生可能会想出如下方法。
方法一:四周平均每周接种新冠疫苗70人次,据此就可以逆向求出四周接种新冠疫苗的总人次,再减去前三周接种新冠疫苗的人次。
方法二:第一周接种新冠疫苗的较多,把其中30人次转移到第二周,则前三周都接种新冠疫苗60人次,要使平均每周接种新冠疫苗70人次,这样就还差30人次,再加上第四周接种新冠疫苗的70人次,得出第四周接种新冠疫苗的人次要达到100才可以。
方法三:把第一周中的10人次转移到第二周,再把第一周的10人次转移到第三周,这样前三周接种新冠疫苗的人次分别是70,40,70,那么,用第二周差的30人次再加上第四周需要达到的70人次,答案是100人次。
方法四:第一周保留30人次,把60人次都转移到第四周,这样,这四周距离要求的70人次,分别差了40人次、40人次、10人次、10人次,40+40+10+10=100,答案同样是100人次。
平均数算法的逆向倒推和移多补少的基本思想方法均可以破解这道题。方法二、三、四都是运用的移多补少的方法,区别是基准不同,它们分别以60,70,30为基准。当然,方法还有很多,但是都要经过深入思考才能得出。
设计的活动二并未直接要求学生计算平均数,而是通过现实情境告诉学生,平均数可以反映两组数据的整体水平,要想比较出两组数据的高低,就必须用平均数加以确认。求平均数的本质实际上是移多补少,实际计算时,也可以运用移多补少的办法,而且怎么“移”、怎么“补”也存在方法的多样性,学生在经历活动二各种各样的“移花接木”后,就能掌握计算平均数的表象,这些宝贵的经历会促使学生在每次计算平均数时,都能熟练运用平均数的内在规律。
三、联系旧知,对比辨析
完成上述两个学习活动后,学生对平均数有了细致的了解,此时,受知识迁移的影响,学生极有可能将“平均数”和“平均分”混淆。
“除法的初步认识”对平均分有着明确的定义,将总数分成每份一样多的若干份,平均分是一种结果一定的分配方案,而不是方法,无论采用哪种分法,最终的结果是一样的,而且无论初次分配如何混乱,通过移多补少都可以达成平均分的目的,计算出的结果是实际操作后的客观事实,或者说是可以预见的事实。
而平均数则是一个统计概念,它在现实生活中未必对应着分配的结果和操作,甚至不具备可操作性。学生学习平均数之前已经学过平均分,平均分是“物品总数÷分的份数=每份数”,例如,甲有某上市公司3万股股票,乙有该上市公司5万股股票,一共有8万股股票,如果平均分,则甲、乙各得到4万股。而平均数的计算公式为“数据总和÷个数=平均数”。
活动三可以进一步深化平均数的统计概念。
【活动三】有调查报告称:“放开三胎后,甲市每对夫妻平均生育2.5个子女;同期的国外某城市则是平均2.5人生育1个子女。”请你想一想,其中的“2.5人”是什么意思?
通过学生的回答可知,在他们心目中,“0.5”是未成年人,“2.5人”表示两个成人和一个未成年人。出现这样令人啼笑皆非的答案,表明学生还没有对平均数的统计概念有深刻印象。半个人是不存在的,当A对夫妻育有2个子女,B对夫妻育有3个子女,平均每对夫妻就育有“2.5个子女”。以上报道可以理解为“甲市每两对夫妻加起来育有5个子女”和“同时期国外某城市平均5人就育有2个子女”。教师可以继续问“每名学生平均每天阅读1.5小时”中的“1.5小时”作何解,此处的“1.5小时”则是一个具体量。教师要引导学生理解平均数的统计意义与实际意义的联系与区别。
平均数是一个统计概念,其数值在具体情境中也没有正式的“身份”,因此,要将其与平均分概念彻底区分开,平均分中的每个数字都是实指,而平均数则是虚构的,如生育率统计中的“2.5人”就是虚指,因为不存在半个人这一说,而到了统计中,它又是合理的,此处的0.5是移多补少造成的结果,只要将所有“0.5”合起来,会得到一个整数。平均数的虚拟性还体现在不可操作性,如7天的平均气温可以进行理论计算,但是人们无法将7天的气温叠加到一块,然后平均分成7份,也不可能将今天的气温转移3℃到昨天。但是,如果换成是7个人摘苹果,平均每人摘得的苹果数却可以“操作”出来——先将所有苹果收集起来,然后平均分给7个人。
“变教为学”中强调学习内容要“实现关联”,指的是课程既要体现知识,又要反映生活,因此,最后设计活动四,让学生在生活中处处看到平均数的身影。
【活动四】说说你在生活中的哪些地方见过平均数?
活动四的问题很开放,待学生举例后,教师可以继续补充完善相关知识。
“变教为学”要求学习内容凸显数学本质、渗透数学文化、实现知识间的关联。因此,对“平均数”的教学设计首先要突出平均数的本质——选择中间值估计大数;其次,需要渗透平均数的文化,回顾平均数的发展史;最后,把平均数与学生已经学过、学会的平均分联系起来,对照辨析,弄清平均数的统计功能与统计特性。
