小学生数学学习偏差认知归因及教学对策

江苏无锡市春城实验小学（214028）王炎萍

数学学习中，学生的认知往往是伴随着错误而不断进阶的。学生的错误是需要教师研究的一个重要内容。要想真正提高学生的数学学习质量，就必须重视研究和分析学生解数学题时出现的错误，最大限度帮助学生找到数学解题错误的真正原因。

一、数学学习偏差认知的归因

1.受学习动机影响

学习动机是激发和维持个体进行活动，并使该活动朝着某一目标前进的心理倾向或动力。小学生的学习动机较弱，学习缺乏主观能动性，不够自觉。比如，一部分学生在看完教师批改的作业后，不需要教师讲评就能订正，这说明学生出现偏差认知的原因是学习动机不够强烈。另外，高年级学生的学习动机比低年级学生的学习动机弱。究其原因，是小学数学知识的编排是螺旋上升的，难度逐渐增加。一些学生学习时思考得不深入、不全面，渐渐地，就产生畏难情绪，在“我不行”“我不会”等不良心理的暗示下，逐渐丧失学习数学的信心和动机。

2.受直觉思维影响

直觉思维，是指对一个问题未经分析，仅依据个人的感知迅速对问题做出判断、猜想的思维方式。面对具体数学问题（知觉对象）时，问题的不同部分对学生大脑的刺激有强弱的差别，在大脑中，强知觉对象会抑制弱知觉对象，造成学生对弱知觉对象的暂时性遗忘，表现在学习上就是出现不同程度的偏差认知。小学生心理、生理的发展具有一定的特殊性，他们容易受直觉思维的影响，仅凭经验做题，缺乏对题目的观察与思考。

比如口算25×4÷25×4时，很多学生会脱口而出“等于1”，是因为他们一眼看到了25和4这对“黄金搭档”，想当然先将它们相乘得到100，再算100÷100就得到1。“25×4=100”这个刺激尤为强烈，以至于学生一时遗忘了要考虑运算顺序，从而出现错误。这是因为学生受直觉思维的影响，在没有厘清思路的情况下就开始解题，把握不准其中蕴含的数量关系，因此产生偏差认知。

3.受思维定式影响

数学学习中的思维定式是指学生在先前的数学学习活动中形成的一种相对稳定和习惯的思维模式。思维定式具有双重性，它可以帮助学生自主学习，建构知识体系，即正迁移；它也会束缚学生的思维，形成思维障碍，造成学生出现偏差认知，即负迁移。

例如，学习“求一个数的几分之几是多少”后，在遇到直接相加减的题目时，学生会受思维定式影响而出现错误。如“90吨增加吨是多少吨？”，有些学生给出的答案是再如，已知图1中阴影部分的面积是50平方厘米，求圆环的面积是多少平方厘米。学习了圆环的面积后，学生已经习惯了用两个圆的半径平方之差乘π求出圆环的面积，现在遇到这样的问题，受思维定式的影响，还是想用两个圆的半径平方之差乘π来解题。

图1

4.受晕轮效应的影响

晕轮效应是指人们在交往认知中，对方的某个特别突出的特点、品质会掩盖人们对对方的其他特点和品质的正确理解。具体到数学学习中，晕轮效应表现为学生在认知过程中，习惯由个别推及一般，由部分推及整体，出现以偏概全的错误。

例如，工厂仓库里有50箱冰墩墩和60箱雪容融，工人要把冰墩墩装运到店面，一辆卡车每次最多能运6箱，至少运多少次才能运完所有的冰墩墩？“60箱雪容融”在本题中明显是一个多余条件，但是由于本题涉及“平均分”数量关系下的“包含除”结构，而60是6的倍数，因此有5.2%的学生列出了“60÷6”的错误算式。

二、转变数学学习偏差认知的教学对策

基于认知心理学，深入分析学生在数学学习中出现偏差认知的原因，有助于教师找到导致学生产生偏差认知的源头。同时，研究积极有效的转变策略为教师提升学生思维品质、多维度转变学生偏差认知提供了可借鉴的经验。

1.转变因学习动机影响产生的偏差认知

（1）教学方式多样化，使学生获得成功体验

小学生的心理特点决定了他们喜欢在游戏中学习，喜欢灵活、生动、有趣的课堂。教师不妨改变课堂教学模式，以转变学生的学习态度，增强其学习动机。

比如，在教学“认识倒数”时，可设计“唱反调”游戏，即要求学生把教师说的话倒过来说一遍。例如，教师说“京东”，学生说“东京”；教师说“过来我上马”，学生说“马上我过来”……学生感受到把话倒过来说是如此地有趣，然后不由得思考：数学中的数能倒过来吗？这样引入新课，学生的注意力就会很集中。再如，根据学习内容的需要设计活动类课程，如“智搭七巧板，巧创造”“巧摆圆片，找规律”“神奇的莫比乌斯圈”等各种各样的综合实践活动，既能让学生综合运用所学知识解释生活中的有趣现象，又能激发学生学习数学的浓厚兴趣，使其学好数学的动机增强。教师应该把主动权交到学生手中，促使学生的观念由“要我学”变为“我要学”，这样学生的学习动机就会变得强烈，从而避免一些不必要的偏差认知。

（2）巧设“坎坷挫折”，消除畏难情绪

要消除学生的畏难情绪，增强他们的学习动机，教师就要站在学生的角度，想他们所想。除利用好学生的错误资源之外，还可以巧妙地设计一些陷阱，结合具体的例子让学生认识到错误在学习过程中难以避免，正确的做法是端正态度，直面错误，找出原因，加以改正。

2.转变因直觉思维影响产生的偏差认知

要消除直觉思维的影响就要强化学生的审题能力。教师可以从培养学生良好的学习习惯入手，强化学生的审题能力。例如要求学生在审题时圈画重点词、关键句等。对于求面积、体积的问题，圈出关键词三角形或圆锥，以提醒计算时乘列方程解决实际问题时，可以把关键句画出来，根据关键句找出等量关系，从而正确列出方程。教师也可以从提升数学阅读理解能力入手。数学阅读理解能力的提升可以帮助学生规避一些不必要的错误。比如：男生有25人，女生有20人，女生比男生少（ ）%。这是训练学生明白解决“谁是谁的百分之几”这类问题的关键是找准单位“1”，用相差的人数除以单位“1”（男生人数）就可以顺利解答。另外，在教学中要注意结合实际问题使学生了解看见“多”和“少”不一定就是加和减。教师还可以从题组训练入手。如教学分数实际问题的练习时可以设计这样一组题：

①织女星的运行速度是14千米/秒，相当于牛郎星运行速度的牛郎星的运行速度是多少？

牛郎星的运行速度是多少？

条件和问题都类似的两道题，解答时需要细心辨别。题①单位“1”未知，可以用除法求出，题②列方程进行解答则更能确保正确率。题组训练可以让学生在对比中直观感受到“长得差不多”的题，解题思路却不相同。这不仅能锻炼学生的审题能力，还能减少直觉思维给学生带来的负面影响。

3.转变因思维定式影响产生的偏差认知

（1）克服思维惰性，发展求异思维

求异思维无论在观察、感知等方面，还是在分析问题和解决问题等方面，都可以避免思维定式负迁移的消极影响。因此，教师在教学中应抓住契机，引导学生从多个角度思考问题，勇于改变原有的思维习惯。

（2）改变思维方向，培养逆向思维

学生解题时往往习惯从条件出发，正向思考，一步步解决问题。可有些问题从正向思考难度较大，如果能改变思维方向，反向思考，问题或许就迎刃而解了。逆向思维的培养是培养创新精神的基础，也是克服思维定式，探索解题捷径的重要手段。

例如：图2中阴影部分的面积是50平方厘米，圆环的面积是多少平方厘米？

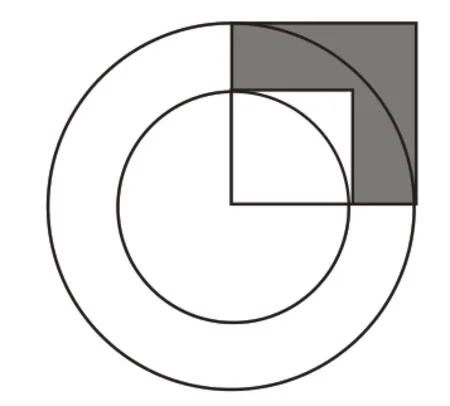
图2

大部分学生在解决这个问题时遇到了困难：根据阴影部分的面积求不出大圆和小圆的半径。在学生囿于寻找半径的思维框架之中时，笔者这样引导：“求圆环的面积一定要知道半径吗？仔细观察圆环的面积公式，其实只要知道什么就可以了？”学生灵光一闪，发现只要知道半径平方的差就可以解决问题了，半径平方的差就是阴影部分的面积，阴影部分的面积×π就是圆环的面积，即50π平方厘米。

可见，当正向思考遇到困难时，可以根据“正难则反”的思路，顺势培养学生的逆向思维，从而帮助他们摆脱思维定式的消极影响。

4.转变因晕轮效应影响产生的偏差认知

要转变因晕轮效应所产生的偏差认知，教师可以在习题设计中根据学生的认知情况有针对性地创编习题。创编习题的过程中要注意以适当的形式、顺序、位置设置相关属性的多余条件，使习题的“练”能练在学生的“痛点”上。量身定制的习题可以促进学生深入理解数学问题，建构知识体系。

如针对以工程问题为代表的“数量与分率”问题，可设计这样的习题：服装厂工人甲制作风衣，每天完成80件，10天完成了总件数的40%，照这样计算，他完成总件数一共要多少天？解决这个问题既可以从数量的角度入手，也可以从分率的角度思考，还可以根据分数除法的数量关系来分析。

解法一：总件数为80×10÷40%=2000（件），完成总件数一共要2000÷80=25（天）。

解法二：把总件数看作单位“1”，每天完成单位“1”的40%÷10=4%，完成总件数一共要1÷4%=25（天）。

解法三：10天完成的件数占总件数的40%，则10天也占总天数的40%。因此，完成总件数一共要10÷40%=25（天）。

通过解答这样的问题，学生懂得解题时首先要甄别条件是否有用：条件的有用无用，是否多余，关键要理解题意，明白问题所求。设置多余条件能促进学生学会厘清数量关系，提取有效信息，解决问题，实现深度学习。经历了这样的训练，学生对具体问题中数量关系的理解变得更加精准，思维更缜密，从而走出因晕轮效应造成的解题困境。

综上，学生的学习动机、直觉思维，思维定式、晕轮效应会引起学生产生数学学习偏差认知。在纠偏策略的探寻与实践道路中，教师要站在学生角度进行思考，丰富教学方式，创新习题设计，巧设一题多解，等等。基于认知心理学深入分析学生数学学习产生偏差认知的深层原因及教学对策，不仅仅是在教学中重视学生心理、遵循学生天性、关注学生学情的重要体现，更是培养学生数学核心素养的有力支撑。

［1］李光树.由思维定式和负迁移引起的学习障碍：小学数学学习障碍研究之三［J］.小学数学教育，2012（10）：3-6.

［2］卢声怡.“多余”并不多余：习题改编的“增加条件”策略与教学价值例谈［J］.小学数学教师，2021（11）：15-19.

［3］孟阳燕.例谈数学学习中思维定式负迁移的克服对策［J］.新课程（综合版），2018（12）：187.