培养学生数感的策略探究——以“小数的初步认识”教学为例

江苏南通师范学校第一附属小学（226004）金 燕

数感是对数与数量、数量关系及其运算结果的直观感悟，这种感悟能让人灵活地运用数学方法来解决实际问题。学生具备数感后，不仅能深刻理解生活中的数的意义和价值，还能促进自身数学思维和创新意识的发展。因此，教师在教学中要培养学生的数感，为学生创造良好的学习条件，创设贴近生活的情境，开展多元的数学活动，让学生在感知、体验与探究数的过程中发展数感。本文中，笔者以“小数的初步认识”教学为例，探究培养学生数感的策略。

一、创设生活情境，在读数中建立数感

数感的建立来自学生的感知，教师不妨从生活出发，创设生活情境，让学生在熟悉的情境中读数，从而使学生加强对小数的感知，初步建立起数感。

【教学片段1】

师：国家规定中小学每年都要组织一次免费体检，前几天，同学们是不是进行了一次体检？大家还记得做了哪些检查吗？

生1：量了身高、体重、血压、心率等。

师：没错，现在老师给大家看一组体检数据（出示体检数据图片，图略），请大家仔细观察，看看图片中有哪些数学信息？

（学生读出图片中的数字，教师随即在黑板上写出数字）

师：86和63都是我们熟悉的整数。那么，另外这些又是什么数呢？

生2：小数。

师：为什么说它们是小数呢？你们是从哪看出来的？

生3：这些数都有小数点。

师：同学们说得真棒！小数点左边是整数部分，右边是小数部分。大家试着读一读3.1，5.2，23.7，10.8，36.58这些数。

生4：三点一、五点二。

生5：二十三点七。

生6：十点八、三十六点五十八。

师：以上同学读得正确吗？

生7：我觉得36.58这个小数应该读作三十六点五八。如果像生6那样读，那么小数部分的五十八就比整数部分的三十六还要大了，这是不对的。

师：生7说得对。为了区分整数部分与小数部分的读法，整数部分就按照一般整数读法来读，小数点读作点，而小数部分则按照从左往右的顺序，将数一个一个读出来，比如，13.36读作十三点三六。现在大家会读了吗？

（教师写出20.08，503.80，0.69……引导学生读小数，不断巩固小数的读法，并写出本堂课的主题“小数的初步认识”）

以上教学片段中，教师首先创设了“体检”这一生活情境，让学生直观地体会测量时不仅会用到整数，还会用到小数，从而使学生对小数有初步感知；接着引导学生读小数，让学生在读小数的过程中加深对小数的认识，逐步建立数感。

二、强化练习体验，在写数中加强数感

数学学习的过程本质上就是实践和体验的过程。在“小数的初步认识”教学中，教师要引导学生写一写，促使学生在练习中进一步了解小数数位的意义，掌握规范的小数写法，从而加强学生的数感。

【教学片段2】

师：一支铅笔的价格是0.72元，一本作业本的价格是1.8元。请大家把听到的小数写下来。

师：一个铅笔盒的价格是27.16元，具体是几元几角几分呢？

生1：27元1角6分。

师：53.29元是几元几角几分呢？

生2：53元2角9分。

师：请大家仔细观察，27元1角6分=27.16元，53元2角9分=53.29元。你们发现了什么？

生3：小数点左边的数字表示多少元；小数点右边第一位数字表示多少角，第二位数字表示多少分。

师：没错。请大家完成练习题。（1）2元3角是（）元；（2）6角是（）元；（3）8分是（）元。

生4：（1）2元3角是（2.3）元；（2）6角是（0.6）元；（3）8分是（0.08）元。

师：同学们已经熟练掌握了元、角、分之间的转换方法。接下来，请同学们完成以下拓展练习。

（1）1角=（）元

（2）12.8元=（）元（）角

（3）5元6角=（）元

（4）85.97元=（）元（）角（）分

以上教学片段中，教师先让学生听写小数，让学生初步掌握小数的规范写法；然后借助元、角、分的知识，让学生在转换的过程中了解小数数位的意义；最后利用拓展练习来巩固小数知识，让学生在写数中加强数感。

三、借助多元活动，在数数中发展数感

数感是无法言传的，因为它是学生在学习过程中自主产生的体验与感悟，而这些感悟通常来自数学活动。因此，在教学中，教师应当多组织数学活动，在读一读、写一写之外，鼓励学生体验多样的数数活动，让学生在数数活动中加强对小数的认识和理解，促进数感的发展。

【教学片段3】

师：我们来玩一个“抓硬币”的游戏。这里有一个小袋子，袋子里有9枚1角硬币，同学们来抓一抓硬币，并将抓出来的硬币数值用元作单位来表示。

（学生分别抓出了1枚、2枚、3枚……9枚硬币，教师带领学生从0.1元数到了0.9元。这时，教师又往袋子里放了1枚1角硬币）

师：现在一共有多少钱？

生1：1元。

生2：10角。

师：没错，1元=10角，10角=1元，1角是1元的十分之一。用一个正方形来表示1元，如何表示其中的0.1元呢？请大家在纸上画一画。

（学生将正方形平均分成10份，给其中1份涂色，如图1）

城市文化地标是具有多种文化含义和象征的文化景观，不仅具备独特的建筑风格与独有的品牌效应，也蕴含了这座城市的文化精神与内在品质。近年来许多地方为增强城市的文化识别度、提升城市文化形象和品质，开始重视对文化地标的挖掘、宣传和推广工作。

图1

师：假如用正方形表示1米，如何表示其中的0.1米呢？

（学生重新画了一个正方形，将其平均分成10份，给其中1份涂色，如图2）_____

图2

师：假如这个正方形表示1，那0.1应该如何表示呢？

（学生将正方形平均分成10份，给其中1份涂色，如图3）

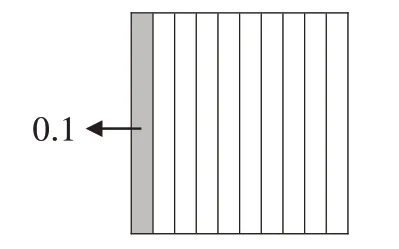
图3

师：有一棵小树目前高1.1米，随着时间的增长，这棵树的高度可能是多少呢？

生

3：1.2米、1.3米、1.4米、1.5米、1.6米、1.7米。

生4：1.8米、1.9米。

生5：2米。

师：怎么数着数着，小数就变成整数了？原来在1和2中间还存在这么多小数呀。

生6：我学习小数之后才知道两个相邻的整数之间还有这么多小数。

以上教学片段中，教师先通过有趣的“抓硬币”游戏，让学生逐渐感知到0.1元与1角和元之间的转化关系，逐渐了解小数的实质就是十进制分数；再利用正方形涂色活动帮助学生建立起0.1的数学模型；最后让学生数一数整数之间的小数，领悟“满十进1”的数学思想，从而发展学生的数感。

四、回归生活问题，在对比中积累数感

数学来源于生活，又服务于生活。教师可以引导学生找一找生活中的小数，并通过对比的方式，逐渐加强对小数的理解，从而逐渐积累数感。

【教学片段4】

师：同学们，想一想在生活中哪里能见到小数？

生1：量体温、称体重……

师：老师有一个疑问，为什么量体温时用小数，而天气预报显示的气温是整数呢？同样都是温度，为什么一个用小数表示，一个用整数表示呢？

生2：因为天气预报中的气温是根据各种情况推断出来的，并不是特别精准，所以用整数表示即可。测量人的体温必须要精准一些，否则就会耽误病情，因此，需要用小数表示。

生3：一般人的体温就在几个整数之间，变化不大，用小数表示更精准。

师：原来是这样呀！

以上教学片段中，教师引导学生观察生活，让学生想一想生活中的小数知识，并通过体温与气温的对比感悟小数的精准性，从而加深学生对小数知识的认识，积累丰富的数感。

五、通过估算训练，在观察中增强数感

在数学中，估算是根据现有条件及有关知识对某种事物的大小或数量做出大致推断，这种推断是合理的。学生在反复的估算练习中会不断提高数感，因此，加强估算训练是增强数感的有效方法之一。教师要根据学生的特点，采取循序渐进的训练方式。通过科学的估算学习训练，让学生在观察中增强数感，进而为以后的计算打下坚实的基础。

【教学片段5】

师：请大家估算一下，教室的门大概有多高？

生1：教室的门比我们都高，这个不好估算呀。

师：如果有一个比我们矮的物体，我们如何估算它的高度？

生2：找一个和这个物体高度差不多的东西来做参考。

师：没错，可不可以这样认为，我们找的那个东西的高度是已知的？

生3：是的。

师：为什么？

生4：只有知道其中一个物体的高度，我们才有估算的基础条件。

师：现在大家有没有什么好方法去估算门的高度？

生5：找一个已知高度的物体和门做比较。

生6：我知道了，用自己的身高和门做比较。

（生6站到门前）

生7：生6的身高是1.4米。我通过观察，感觉门的高度比两个生6的身高累加矮一点，所以门的高度大概是2.6米。

生8：不对，我觉得门的高度大概是2.5米。

师：两个答案差了0.1米，我们需要知道0.1米有多长，才能进行合理估算。

（学生量出0.1米的长度后，再估算）

以上教学片段中，教师先引导学生思考估算方法，让学生在观察中进行粗略估算，随后，在了解某个特定数值的具体长度之后，再让学生进行精确估算。在由粗到精的过程中，学生的估算能力不断提升，学生也在无形中加强了数感。

总之，数感是学生必备的数学核心素养之一。而数感需要在长期的学习过程中不断建立和发展起来。教师不仅要在教学中充分尊重学生的主体地位，还要探索有效的教学方法，设计多元的数学活动，让学生在数学活动中不断体验、感知和探究数，最终建立与发展数感，全面提升数学核心素养。