基于改进Bi-RRT*算法的移动机器人路径规划
2022-02-22叶鸿达涂海燕
叶鸿达, 黄 山, 涂海燕
(四川大学电气工程学院,成都 610000)
0 引言
移动机器人具有自主运行、移动灵活等特点,所以在国防科技、生活服务、生产建设等重要领域具有广阔的开发前景。移动机器人不断普及,若行进路径效率不高,则会严重影响其工作质量[1]。移动机器人路径规划指在障碍物环境下,机器人从起始状态到目标状态找到一条满足自身和环境约束的无碰撞路径[2]。常见的路径规划算法有人工势场法[3-4]、蚁群算法[5]、JPS算法[6]和A*算法[7]等。当机器人自由度、环境建模的复杂度增加时,以上算法的规划复杂度也会呈指数增长,从而出现“维度灾难”问题[8]。因此,上述算法不适合解决高复杂环境下的规划问题。
因不需要对环境进行精确建模,基于随机采样的规划算法在多维空间中具有明显的优势而得到广泛关注[9]。快速探索随机树(Rapidly-exploring Random Tree,RRT)[10]算法在具有复杂环境的多维空间中可以进行有效的路径搜索,对要求微分约束的系统,RRT算法也展现出优异的性能。RRT算法可快速得到一条无碰撞路径,但该路径存在转角过多、非最优、未考虑动力学约束等问题。针对这些问题,国内外已进行了大量的研究工作。文献[11]提出了EPF-RRT算法,该算法在复杂环境下速度更快、路径质量更优,然而EPF-RRT算法虽具有概率完备性,但也无法找到最优路径。文献[12]提出的EGK-RRT算法在满足动力学约束的情况下,相比经典RRT算法显著减少了执行时间,在特殊环境下,比如狭窄通道,其性能超过了RRT算法,但由于EGK-RRT算法不提供最优路径,其生成的路径长度略大于RRT算法生成的路径。
针对RRT算法生成路径质量不高、非最优等问题,文献[13]提出了RRT*算法,该算法在RRT算法的基础上引入了路径代价函数和重布线操作,通过重新选择父节点,使得路径的代价函数值最优。但是,大多数采样算法都具有随机性,随着环境复杂程度和障碍物数量的增加,花费在碰撞检测和重布线等操作上的时间也随之增加,相比RRT算法,在路径质量更优的情况下,收敛到最优路径的时间却更多。针对碰撞检测导致计算效率降低的问题,文献[14]提出一种Lazy-PRM*算法,该算法在通过PRM*建立的拓扑图上使用Dijkstra或者A*算法进行路径搜索,然后再进行碰撞检测,从而提高算法的执行效率;随着采样节点的增多,其算法效率会降低但路径质量却没有显著提高。JORDAN等提出了Bi-RRT*算法[15],该算法从初始位置和目标位置分别扩展生长树,当两棵树之间的最短距离小于阈值Slim,就表示两树相遇,然后从相遇节点各自回溯到根节点,完成路径的规划;该方法减小了目标点位置对规划的影响,使得目标点不局限在一个位置,大幅度提高了RRT*算法的收敛速度,从而提高了整体规划效率。
针对以上算法存在的计算效率低、收敛时间长等问题,本文提出了一种改进Bi-RRT*算法。该算法随着路径长度的变化,采样空间也随之优化,从而减少无效节点的扩展;在节点扩展阶段,引入目标偏向策略,降低算法扩展的盲目性,以降低算法执行的随机性;结合一种NCC-RRT*算法[16],对碰撞检测机制进行优化,并结合双向扩展机制,显著提高了算法的执行效率;最后,对基础Bi-RRT*算法执行流程进行优化,并对生成的路径进行最优节点筛选,提高路径的质量和算法对内存的利用率。通过仿真实验证实了该算法的有效性。
1 问题描述
本章将会对路径规划的可行性和最优性问题进行描述[2]。在进行路径规划之前需要对环境信息建模。本文首先对障碍物进行离散化,使用有限均匀的点表示连续的障碍物。
定义X=(0,1)d是移动机器人的d维配置空间,d∈N,d≥2。其中,Xobs为障碍物空间,Xfree为自由空间,且Xfree=cl(X/Xobs),cl(·)为封闭集合。定义迭代次数N∈N,初始状态xinit∈Xfree,目标状态xgoal∈Xfree,||
xi,xi+1||
表示配置空间中任意两个状态点之间的标准欧氏距离,并且对∀xi,i∈N满足:||
xi,xi+1||
=||
xi+1,xi||
≥0。∀xi,xj∈X,L(xi,xj)表示连接xi和xj的线段,c(xi,xj)表示L(xi,xj)的代价函数值,c(xi)表示从根节点到xi的代价函数值。
定义1路径σ:[0,1]→Rd是有界函数:
1) 如果它是连续的,被称为路径;
2) 如果它是路径,且σ(τ)∈Xfree,∀τ∈[0,1],被称为无碰撞路径;
3) 如果它是无碰撞路径,并且满足σ(0)=Xinit,σ(1)∈cl(Xgoal),被称为可行路径。
问题1 可行路径规划:考虑一个路径规划问题(Xfree,Xinit,Xgoal),可以找到一条路径σ:[0,1]→Xfree,并且σ(0)=Xinit,σ(1)∈cl(Xgoal),否则返回失败。
问题2 最优路径规划:考虑一个路径规划问题(Xfree,Xinit,Xgoal)和一个代价函数c:∑→R+,可以找到一条最优的可行路径σ*,并且c(σ*)=min{c(σ)},其中σ是可行路径,否则返回失败。
2 改进Bi-RRT*算法
2.1 基础Bi-RRT*算法
基础Bi-RRT*算法在保留RRT*算法特性的同时,引入了双向随机树扩展机制,从而加快了算法收敛速度,使RRT*算法的效率得到大幅度提升。
算法1 Bi-RRT*算法伪代码
V←{xinit,xgoal};E←∅;i←0;
Ta←{xinit,E};Tb←{xgoal,E};
cbest←∞;
fori=1 toNdo
xrand←Sample(i);
i←i+1;
(V,E)←Extend(Ta,Xrand);
xconnect←Nearest(Tb,V.xnew);
ccost←ConnectTree(Tb,xconnect,xnew);
ifccost

returnTa,Tb=(V,E);
首先定义从起点扩展的树为Ta,从终点扩展的树为Tb。然后进行算法初始化,设置两棵生成树的初始位置xinit,xgoal和总迭代数N,并对地图进行离散化。通过Sample(i)进行随机均匀采样,分别从xinit和xgoal节点使用Extend(Ta,xrand)扩展随机节点xrand,然后通过Nearest(Tb,V.xnew)在树Tb上找离V.xnew(表示xnew∈V,下同)最近的节点xconnect,再通过ConnectTree(Tb,xconnect,xnew)连接xconnect和xnew,并在迭代数N内不断优化xconnect和xnew之间的代价值,每次迭代结束通过SwapTree(Ta,Tb)使两棵树交替生长。相比Bi-RRT*算法, RRT*算法在执行Extend(Ta,xrand)函数后便进行下一次路径优化迭代。
算法2Extend(G,xrand)
V′←V;E′←E;
xnearest←Nearest(G,xrand);
xnew←Steer(xnearest,xrand);
ifNotObstacleFree(xnew,xnearest) then

Xnear←NearVertex(G,xnew,|V|);
for allxnear∈Xneardo
ifNotObstacleFree(xnew,xnear) then
_continue;
_ccost=c(xnear)+c(xnew,xnear) ;
c(xnew)=min(ccost)
xmin=xnear;
V′←V′ {xnew};
E′←E′ {xnew,xmin};
for allxnear∈Xnearxmindo
ifNotObstacleFree(xnew,xnear) then

ifc(xnear)>c(xnew)+c(xnew,xnear) then
xparent←xnear.parent;
E′←E′{xparent,xnear};
_E′←E′{xnew,xnear};
-
returnG′=(V′,E′);
其中:Nearest(G,xrand)在树G中搜索离xrand最近的节点xnearest;Steer(xnearest,xrand)在xnearest和xrand连线上,是以xnearest为起点扩展相应步长得到的节点xnew;NearVertex(G,xnew,|V|)在以xnew节点为圆心、以R为半径的范围内搜索树G上的节点,组成集合Xnear;第7~11行伪代码计算xnew的最小代价函数值min(ccost),并将其设为xnew的代价函数值,将对应的节点xmin设为xnew的父节点,然后更新节点集V′和边集E′。第13~21行伪代码更新Xnear的父节点及其代价函数值。NotObstacleFree(xi,xj) 为碰撞检测函数,表示xi和xj连线之间存在障碍物。
2.2 NCC-RRT*算法
NCC-RRT*算法主要用来解决RRT*在碰撞检测上耗费大量计算时间而产生收敛速度慢、效率低及容易被困于狭窄通道环境等问题[15]。NCC-RRT*算法的核心思想是采用碰撞风险评估策略代替原始的碰撞检测策略,从而剔除碰撞检测函数,提高RRT*算法的收敛速度和效率。
2.2.1 碰撞风险评估函数
Line(xnew,xnear)的碰撞风险评估函数[15]表示为
(1)
式中:N表示在边L(xnew,xnear)上均匀选择N个点;H(pi)表示任意一个点pi的碰撞风险
(2)
式中:n表示环境中障碍物点的数量;hj(pi)表示任意一个障碍物点对点pi的影响
(3)
式中,d表示环境中障碍物点到pi的欧氏距离。
GaussCollisionAssess(xnew,xnear)取值范围为0~1,cGauss=kp×GaussCollisionAssess(xnew,xnear)表示边L(xnew,xnear)实际碰撞情况,当cGauss≥kp/10时,边L(xnew,xnear)必定发生碰撞。
2.2.2 改进碰撞风险评估函数
NCC-RRT*算法使用地图中所有障碍物点评估L(xnew,xnear)的碰撞情况,但当离散障碍物点数量较多时,GaussCollisionAssess(xnew,xnear)的时间复杂度远远超过NotObstacleFree(xi,xj) 。基于此问题,本文在L(xnew,xnear)上仅使用边上存在的障碍物点O3对p1进行碰撞风险评估,如图1所示。

图1 L(xnew,xnear)碰撞风险评估Fig.1 Collision risk assessment of L(xnew,xnear)
在图2中实验,静态环境地图大小为x=y=600 m,起点为[200 m,300 m],终点为[400 m,300 m],扩展步长为15 m,标准差σ=2.2,kp=360000,记录30次实验的平均数据作为结果保存在表1中。
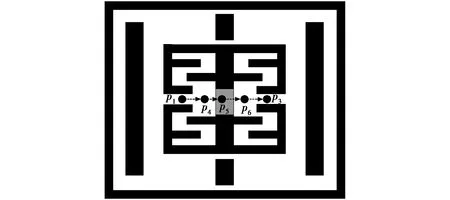
图2 静态环境地图Fig.2 Static environment map

表1 碰撞风险评估函数计算时间数据Table 1 Calculation time of collision risk assessment function s
如图2所示,在L(p1,p3)上均匀选择3个点p4,p5,p6,将L(p4,p6)上的障碍物透明化以方便识别p5。标准碰撞风险评估函数使用环境中所有障碍物对点p4,p5,p6进行风险评估,改进后把L(p4,p6)上的障碍物离散为n个障碍物点Oi,再对点p4,p5,p6进行风险评估,其中,障碍物点Oi到点p4,p5,p6的距离用欧氏距离表示,最后把相应的点坐标代入式(1),即可评估点p4,p5,p6各自的碰撞风险。
根据表1数据可知,标准碰撞风险评估函数的计算时间大约是0.29 s,与环境中障碍物数量成正比,对其改进之后,计算时间与待评估的边上存在的障碍物点数量相关,计算时间大约是0.001 2 s。环境中所有障碍物点和边上存在的障碍物点数量的差距与环境地图相关,由于图2大小为X=Y=600 m,环境中障碍物数量和边上的数量差距极大,因此,算法改进后的计算效率得到大幅度提高。
2.3 动态目标区域采样
标准RRT*算法使用全局均匀采样策略获得地图的环境信息,却导致树生长具有随机性、计算效率低和内存空间大量浪费等问题产生,因此,本文提出一种动态目标区域采样策略,其原理如图3所示。
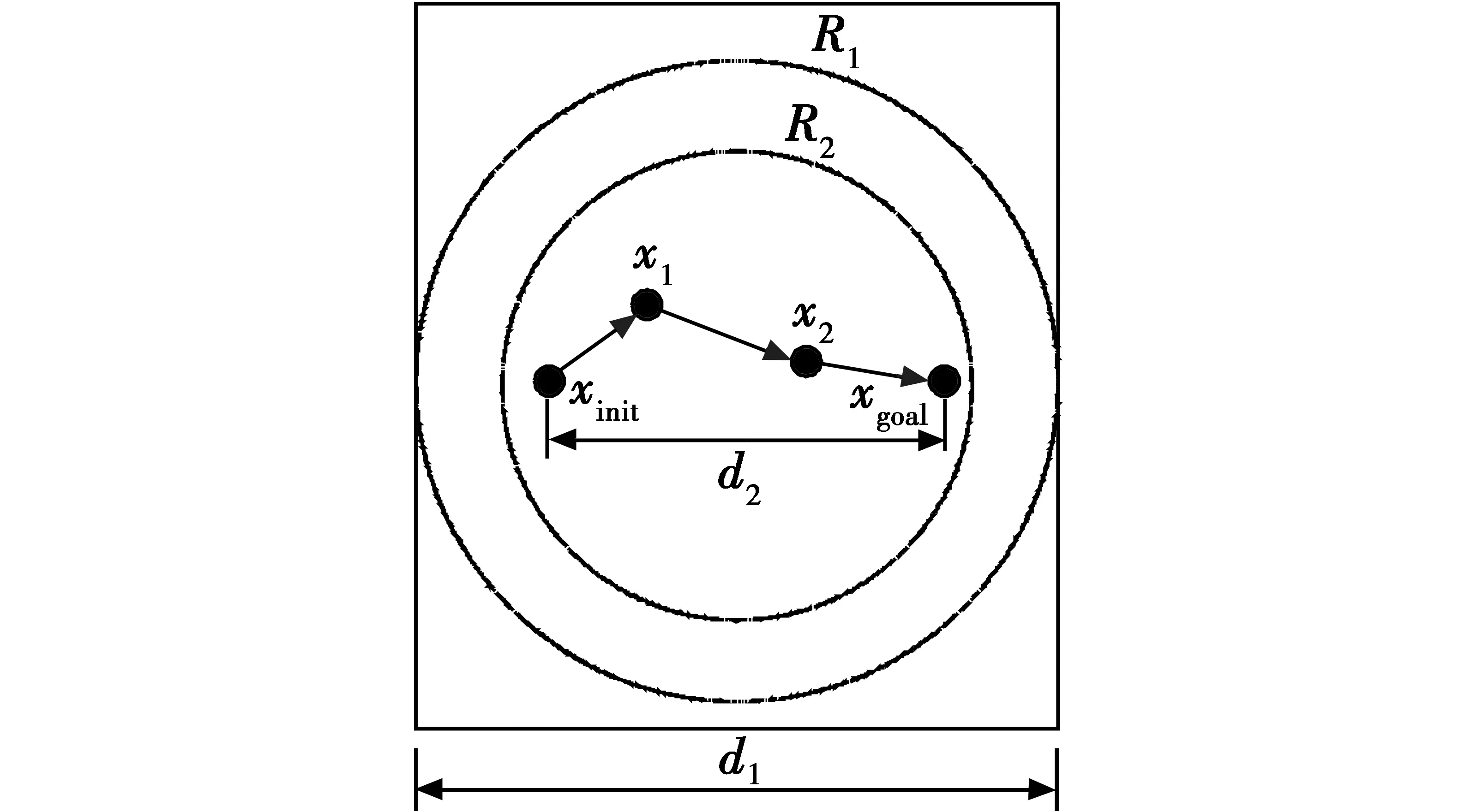
图3 动态圆形区域采样策略Fig.3 Sampling strategy of dynamic circular area
该采样策略在未找到可行路径前,以矩形地图的短边d1为直径构建圆形采样区域R1,当搜寻到可行路径,便以路径长度d2为直径构建圆形采样区域R2,在路径不断优化的过程中,圆形采样区域会逐渐缩小,从而减少无效采样节点数,提高算法收敛速度和内存利用率,构建动态圆形区域采样的伪代码如下。
算法3 动态圆形区域采样算法伪代码
r=radius×sqrt(rand(1));
seta=2×π×rand(1);
point.x=circle_center.x+radius×cos(seta);
point.y=circle_center.y+radius×sin(seta);
returnpoint;
算法原理:其中rand(1)均匀生成0~1之间的随机数,r∈[0,radius],seta∈[0,2π],通过极坐标法均匀生成在以circle_center为圆心、以radius为半径圆内的采样点。
2.4 扇形区域树枝生长策略
尽管动态目标区域采样策略使采样节点尽可能分布在有用的区域,但树生长依然具有随机性,为使树生长具有导向性,结合贪心思想和人类直观思维,本文提出一种扇形区域树枝生长策略,其原理如图4所示。

图4 扇形区域树枝生长策略Fig.4 Branch growth strategy in sector area
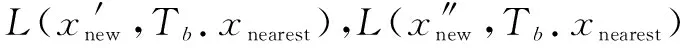
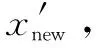
2.5 路径优化
针对Bi-RRT*算法生成的初始路径存在大转角、交叉线和冗余节点从而导致算法收敛速度慢以及在复杂环境下不适合机器人进行轨迹跟踪等问题,本文对标准Bi-RRT*算法的优化策略进行改进,主要分两个阶段。第一阶段:采用快速扩展优化策略,在未搜索到初始路径之前采用双树扩展机制,加快路径搜索速度,在搜索到初始路径后,提取Tb树中存在于路径中的节点并与Ta树组合成一棵单树,在剩下的迭代次数中对组合的Ta树采用RRT*算法的优化思路进行重布线操作。第二阶段:算法收敛后生成的初始路径往往存在冗余的节点,使得路径不够平滑,针对此问题,通过冗余节点剔除方法[17]对路径进行优化,从而得到适合机器人跟踪的路径。如图4所示,定义初始路径节点集合为V,从xgoal开始依次遍历集合中的每个节点xi,如果L(xgoal,xi)边上无碰撞发生,此时的节点xi为冗余节点,如果发生碰撞,则碰撞点的父节点为有效节点,将其加入集合V′,通过该方法得到的优化路径如图5实线所示,其中虚线为初始路径。
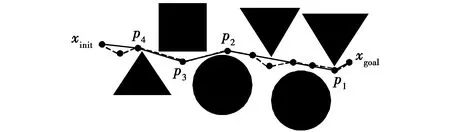
图5 冗余节点剔除Fig.5 Redundant node elimination
3 仿真实验与分析
3.1 实验环境
假设机器人为理想圆点,为验证改进Bi-RRT*算法的有效性和搜索效率,在Matlab R2019b软件中进行实验。PC配置:Windows 10 OS,CPU为Intel Core i5-9400F,RAM为16 GiB,分别对RRT*,NCC-RRT*,Bi-RRT*和改进Bi-RRT*算法进行仿真,为确保数据准确性,统计30次实验的平均数据作为实验结果。
3.2 实验分析
3.2.1 静态环境地图一
静态环境地图一大小为x=y=600 m,规划起点为[100 m,300 m],终点为[500 m,300 m],扩展步长为15 m,标准差σ=2,kp=360 000,路径长度标准阈值设为495 m,当采样节点数大于15 000或路径长度小于标准阈值时停止搜索。图6对比RRT*,NCC-RRT*,Bi-RRT*和改进Bi-RRT*算法在静态环境地图一中的仿真结果;表2记录了每个算法30次实验的平均数据。

图6 静态环境地图一仿真结果Fig.6 Simulation result of static environment map Ⅰ

表2 静态环境地图一仿真实验数据Table 2 Simulation experiment data of static environment map Ⅰ
3.2.2 静态环境地图二
路径长度的标准阈值设置为755 m,其余参数同2.2.2节。当采样节点数大于15 000或路径长度小于标准阈值时停止搜索。图7对比了RRT*,NCC-RRT*,Bi-RRT*和改进Bi-RRT*算法在静态环境地图二中的仿真结果;表3为每个算法30次实验的平均数据。
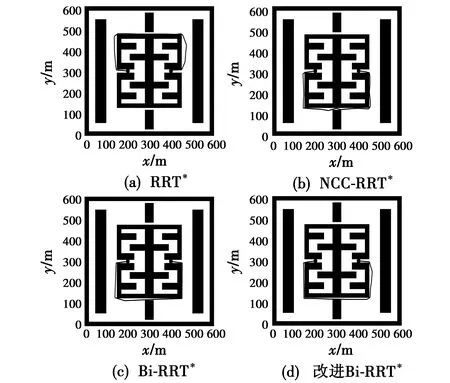
图7 静态环境地图二仿真结果Fig.7 Simulation result of static environment map Ⅱ
根据表2数据可知,在静态环境地图一中RRT*和Bi-RRT*算法由于节点采样和树扩展的随机性,相比NCC-RRT*和改进Bi-RRT*算法需要更多的搜索时间和迭代次数才能收敛;由于NCC-RRT*算法使用碰撞风险评估策略代替了碰撞检测,NCC-RRT*算法的执行效率得到大幅度提高,在迭代上限内NCC-RRT*算法可以收敛;根据表3数据可知,静态环境地图二的类型不属于S型,其最短路径和搜索复杂度比静态环境地图一更复杂,其搜索时间和迭代次数均显著增加,但RRT*,NCC-RRT*和Bi-RRT*算法仍能在迭代上限15 000次内收敛;综合表2、表3的数据可知,由于改进Bi-RRT*算法使用了改进碰撞风险评估策略,并且在节点采样机制、树生长的导向性等方面做出了改进,其执行效率相比RRT*,NCC-RRT*和Bi-RRT*算法提高了约54%,38%和30%。

表3 静态环境地图二仿真实验数据Table 3 Simulation experiment data of static environment map Ⅱ
4 结论
针对RRT*算法在道路狭窄、障碍物较多的环境下执行效率低、收敛速度慢和路径曲折等问题,本文结合NCC-RRT*算法,并对其碰撞风险评估函数进行改进,再通过动态目标区域采样、扇形区域树枝生长和路径优化等方法,提出了一种改进Bi-RRT*算法。仿真实验表明,在相同的迭代上限和收敛阈值内,改进Bi-RRT*算法相比NCC-RRT*算法提高了路径质量和搜索效率,显著减少了迭代次数,在更短的时间内可收敛到满足要求的最优路径。
