共轴八旋翼无人机神经自适应滑模控制设计

2022-02-22郭乃欢熊晶晶

电光与控制 2022年2期

郭乃欢，熊晶晶

(中国计量大学机电工程学院，杭州 310000)

0 引言

近年来,由于优越的垂直起降性能、简单的机械结构，以及在搜救、环境监测、城市监控、测绘、航拍、电力检测、精准农业等军事和民用领域的广泛应用，多旋翼无人机越来越受到国内外学者的关注[1-3]。相关学者提出了许多控制方案来实现多旋翼无人机的飞行控制，例如PID控制[4]、反步控制[5]、滑模控制[6]、自抗扰控制[7]和自适应控制[8]等。

面对各种复杂的飞行环境，多旋翼无人机在飞行过程中不但同时受到空气阻力、重力和陀螺效应等多种物理效应的作用，且极易受到系统未建模项、参数摄动项、外界气流干扰的影响，从而导致系统控制性能严重下降[9]。针对该问题，研究人员普遍考虑使用对各种干扰具有强鲁棒性的滑模控制(SMC)作为解决方案[10-13]。 ZEGHLACHE等[10]针对八旋翼的容错控制问题，提出了一种基于神经网络和区间二型模糊控制的串级容错滑模控制器，分别利用神经网络和区间二型模糊控制来逼近和设计控制器的等效控制与切换控制部分，有效降低了控制器的抖振，并增强了系统的鲁棒性；YANG等[11]提出一种自适应模糊增益滑模控制方法来解决四旋翼无人机的姿态跟踪问题，在飞行器运动学和动力学模型的基础上，设计了滑模控制器，并利用模糊控制使趋近律参数根据模糊规则实现在线的自适应调整，有效削弱了系统的抖振，提高了控制性能；XIONG等[12]根据微型四旋翼无人机的动力学模型，将系统分为全驱动和欠驱动两个子系统，使用终端滑模控制实现了对全驱动子系统的控制，针对欠驱动子系统，将其转化为相应级联形式后，最终利用滑模控制完成了子系统的控制；MU等[13]提出了一种针对四旋翼飞行控制的积分滑模控制方案，利用PID控制实现了高度和偏航通道的跟踪，并基于积分滑模控制建立内环和外环来完成剩余位置和角度状态量的跟踪控制。

上述文献所提出的滑模控制方案大多是在得到系统全面且准确的动力学模型前提下开展的，而在实际飞行中，无人机准确的动力学模型极难获取。针对该问题，本文的主要贡献如下：首先，充分考虑了以系统不确定项和外界干扰项为主的系统未建模项，并利用径向基神经网络的万能逼近性对其进行在线逼近，因此，设计控制器时不需要系统准确的动力学模型；其次，将动力学系统划分为全驱动和欠驱动两个子系统，削弱了系统欠驱动特性对控制器设计的影响，避免了常规内外环滑模控制器设计中由期望位置信号反解期望欧拉角信号的解耦过程；最后，摒弃了容易陷入局部最优的梯度下降法，通过Lyapunov稳定性分析来设计网络权值的自适应律，并最终完成共轴八旋翼无人机自适应滑模控制器的设计。

1 共轴八旋翼无人机动力学模型

共轴八旋翼无人机的结构如图1所示[14]。该结构类似于在四旋翼无人机每个机臂的末端配置了两个同轴且反向旋转的转子对。首先，以飞行器质心为坐标原点建立机身笛卡尔坐标系RB；其次，建立大地笛卡尔坐标系RE；最后,通过欧拉-拉格朗日建模方法建立共轴八旋翼飞行器的动力学模型。动力学方程为[14]

(1)

式中:[xyz]T表示无人机质心在大地坐标系下的位置矢量;[φθψ]T表示飞行器在大地坐标系下的欧拉角矢量;[pqr]T表示无人机在机身坐标系下的角加速度矢量;m是飞行器的总质量;g是重力加速度;Ωr=Ω2+Ω3+Ω6+Ω7-Ω1-Ω4+Ω5-Ω8,Ωi表示第i个转子的角速度，i=1,2,…,8;Ix,Iy,Iz分别代表飞行器沿3个坐标轴方向的转动惯量;Jr为飞行器转子的转动惯量;Ki(i=1,2,…,6)为阻力系数;di(i=1,2,…,6)为系统未建模项，主要由模型不确定项和外部干扰项构成。

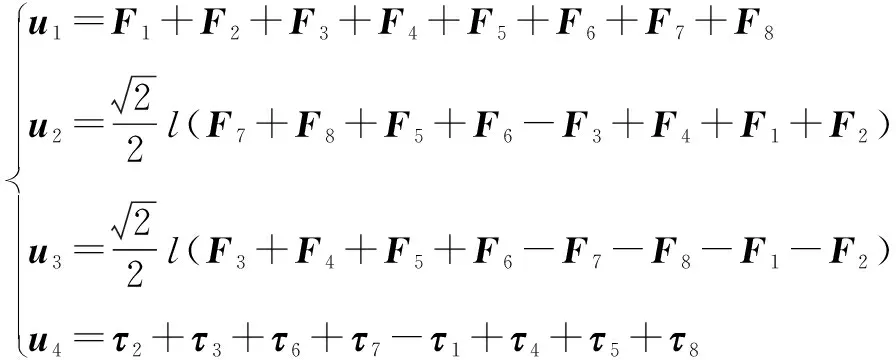
(2)

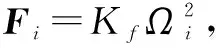
假设1 滚转、俯仰和偏航欧拉角φ,θ,ψ的取值范围皆为(-π/2，π/2)。

图1 共轴八旋翼无人机Fig.1 Coaxial octorotor UAV

2 控制器设计

共轴八旋翼无人机系统的控制结构如图2所示。

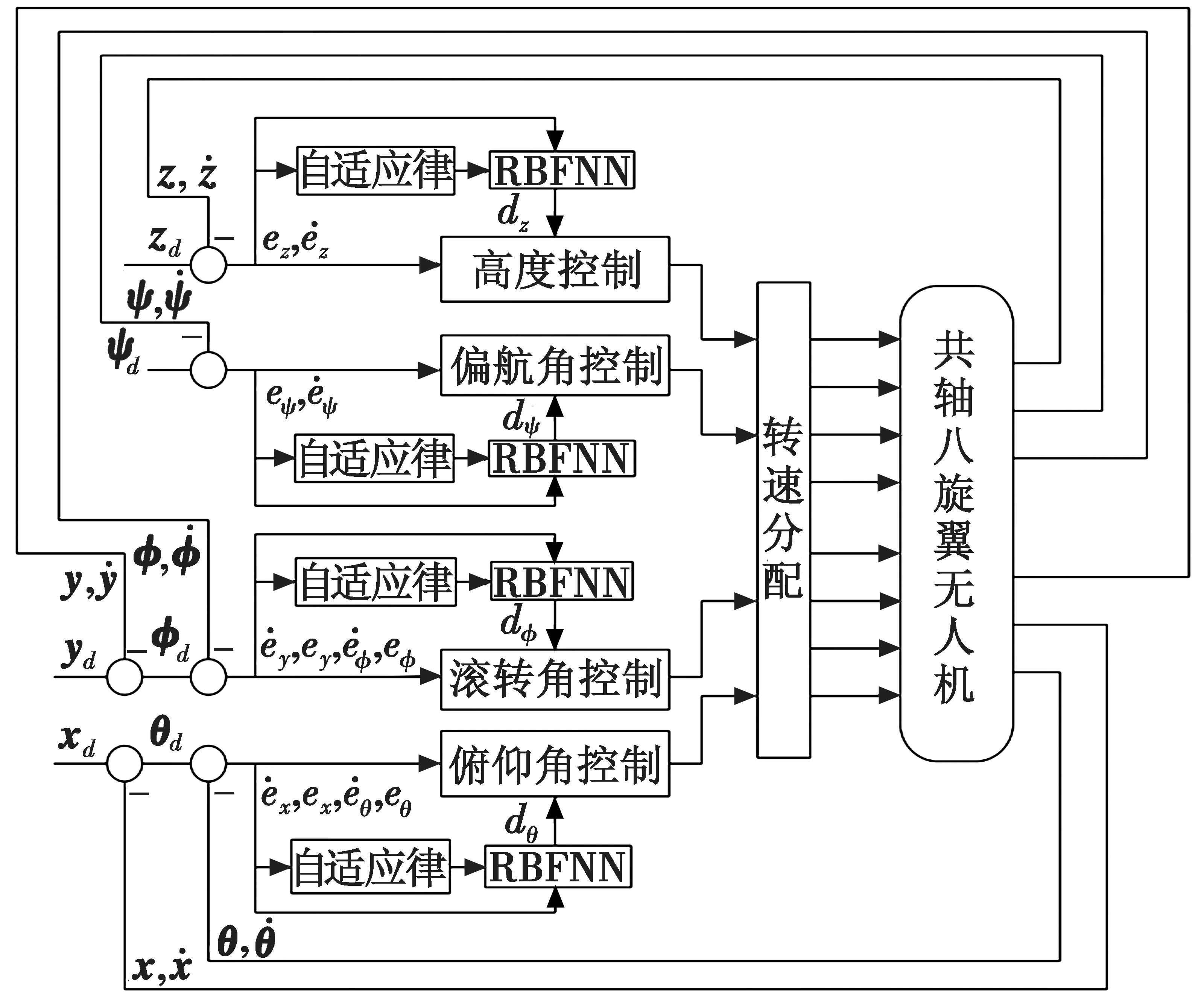
图2 共轴八旋翼无人机的控制结构框图Fig.2 Block diagram of control structure of coaxial octorotor UAV

上下运动(z),左右运动(φ,y),前后运动(θ,x)和偏航运动(ψ)为无人机的4种基本运动形式，而这4种运动分别通过控制总升力u1、滚转力矩u2、俯仰力矩u3和偏航力矩u4的大小来实现。因此，根据以上无人机飞行运动的耦合机理，将共轴八旋翼无人机分为两个子系统，即全驱动子系统(z,ψ)与欠驱动子系统(x,y,φ,θ)。

2.1 全驱动子系统控制器设计

全驱动子系统动力学方程如下

(3)

式中，fz,gz,fψ,gψ分别为

(4)

高度和偏航通道的跟踪误差定义为

(5)

滑模面定义为

(6)

式中，系数cz,cψ>0。

理想控制律如下

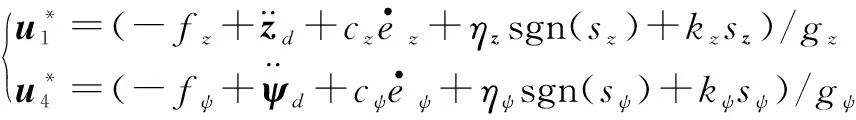
(7)

式中，指数趋近律参数ηz,ηψ,kz,kψ皆大于0。

利用径向基函数神经网络(RBFNN)的万能逼近特性对函数fz,fψ进行逼近[15]，RBFNN的网络结构如图3所示。

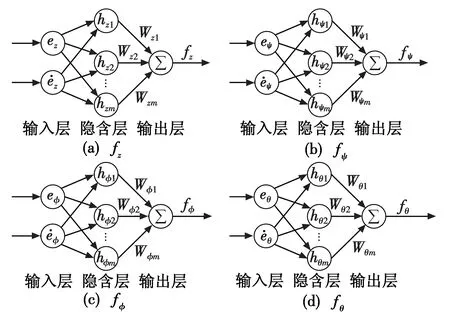
图3 径向基函数神经网络结构Fig.3 The structure of RBFNN

具体算式为

(8)

式中：xz和xψ是网络输入矩阵；βz和βψ为隐含层高斯基函数中心点的坐标向量矩阵；bz和bψ为隐含层高斯基函数的宽度矩阵；hz j和hψj是隐含层第j个神经元的输出；Wz和Wψ是理想网络权值；εz和εψ是网络逼近误差。

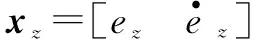
(9)

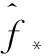
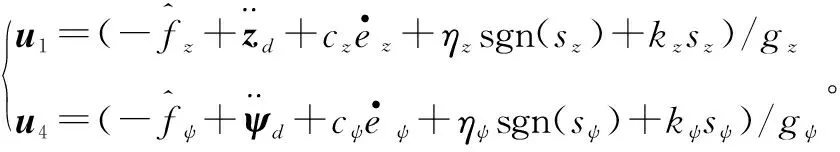
(10)

2.2 全驱动子系统稳定性分析

由式(3)、式(6)、式(8)～(10)得滑模面对时间的导数为

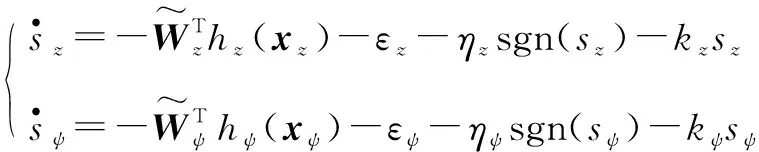
(11)

定义如下Lyapunov函数

(12)

式中，γz,ψ>0。

由式(11)、式(12)得Lyapunov函数的导数为

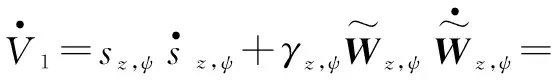
(13)

定义如下网络权值自适应律

(14)

将式(14)代入式(13)得

(15)

2.3 欠驱动子控制器设计

欠驱动子系统动力学方程如下

(16)

式中，fφ,gφ,fθ,gθ分别为

(17)

跟踪误差定义为

(18)

滑模面定义为[16]

(19)

式中：系数c1,c2皆小于0；c3,c4,c5,c6皆大于0。

理想控制律如下

(20)

式中，指数趋近律参数ηφ,ηθ,kφ,kθ皆大于0。

利用RBFNN的万能逼近特性对函数fφ和fθ进行逼近[15]

(21)

式中：xφ和xθ是网络输入矩阵；βφ和βθ为隐含层高斯基函数中心点的坐标向量矩阵；bφ和bθ为隐含层高斯基函数的宽度矩阵；hφ j和hθ j是隐含层第j个神经元的输出；Wφ和Wθ是理想网络权值；εφ和εθ是网络逼近误差。

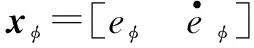
(22)

(23)

2.4 欠驱动子系统稳定性分析

由式(16)、式(19)、式(21)～(23)得滑模面对时间的导数为

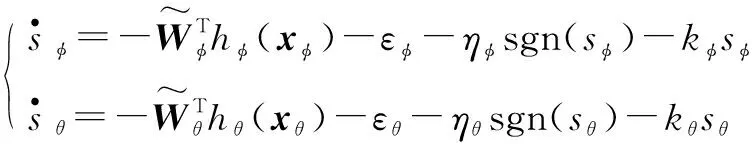
(24)

定义如下Lyapunov函数

(25)

式中，γφ,θ>0。

由式(24)、式(25)得Lyapunov函数的导数为

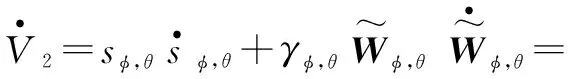
(26)

定义如下网络权值自适应律

(27)

将式(27)代入式(26)得

(28)

综上，由全驱动子系统和欠驱动子系统的渐近稳定，可得共轴八旋翼无人机系统渐近稳定。

3 仿真分析

本节以式(1)作为真实共轴八旋翼无人机的仿真动力学模型，通过Matlab/Simulink平台进行了飞行控制的仿真实验，Simulink仿真框图如图4所示，表1为无人机仿真动力学模型参数的具体数值。

图4 Simulink 仿真框图Fig.4 Simulation diagram of Simulink

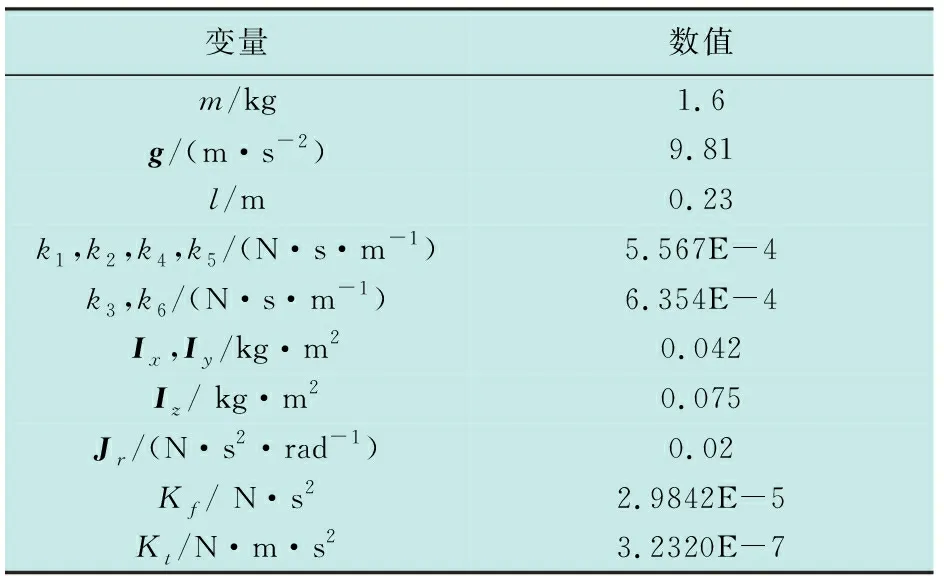
表1 动力学模型参数Table 1 Parameters of dynamic model

期望的位置路径分别为xd=sin 0.1t，yd=cos 0.1t，期望的高度变量为zd=0.5t，期望偏航角ψd=0.1sin 0.5t。滚动和俯仰角的初始值设置为：[φ0θ0]=[00]，单位为rad。仿真过程中，利用di=0.8sin 0.1t(i=1,2,…,6)来模拟系统未建模项和外部干扰等因素；模型参数的不确定性取为20%，即m,Ix,Iy,Iz的值都减少20%。图5为位置(x,y)的跟踪轨迹。图6为位置z和偏航角ψ的跟踪轨迹。图7为滚转角φ和俯仰角θ的变化过程。

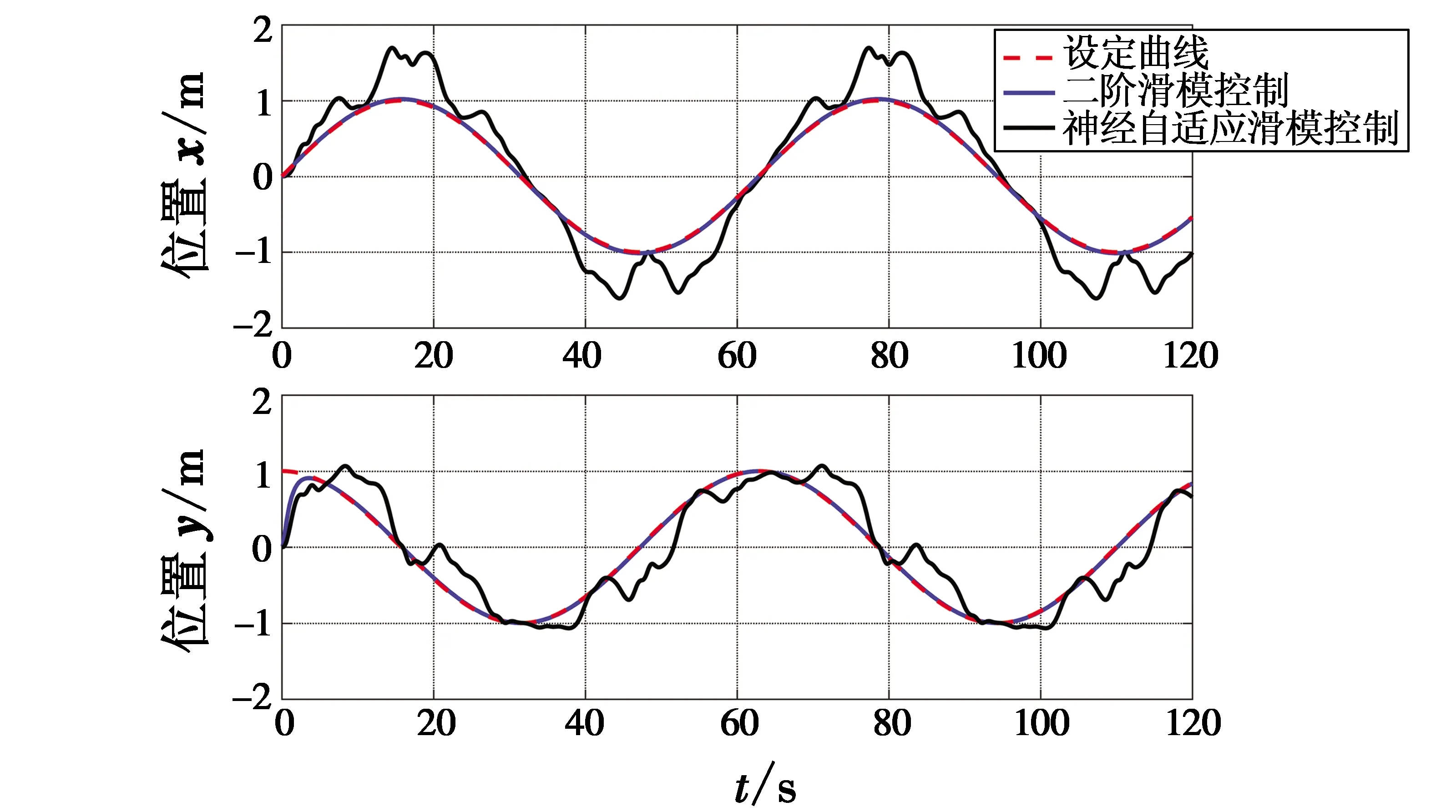
图5 位置(x,y)Fig.5 The positions (x,y)

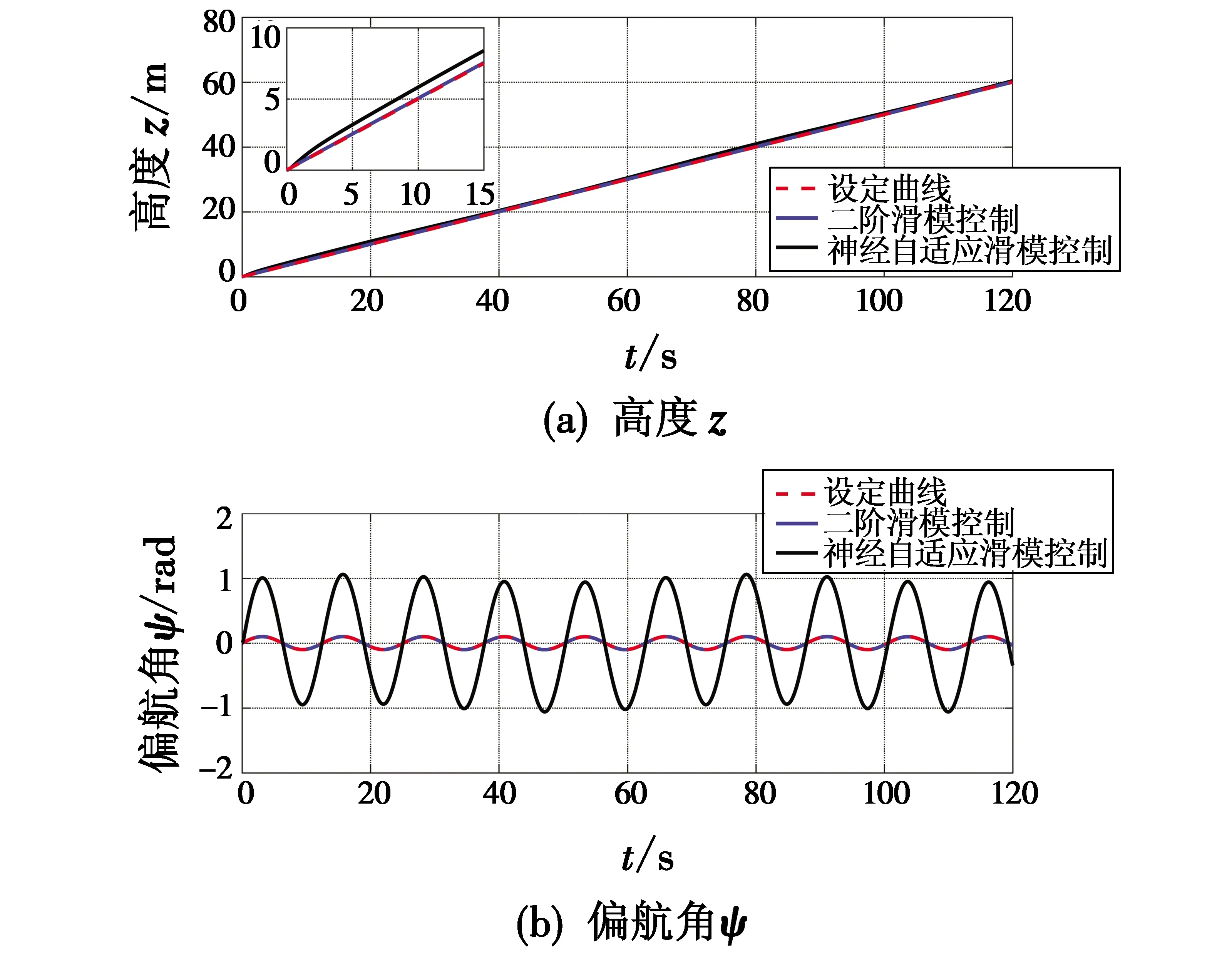
图6 高度z和偏航角ψFig.6 The altitude z and the yaw angle ψ

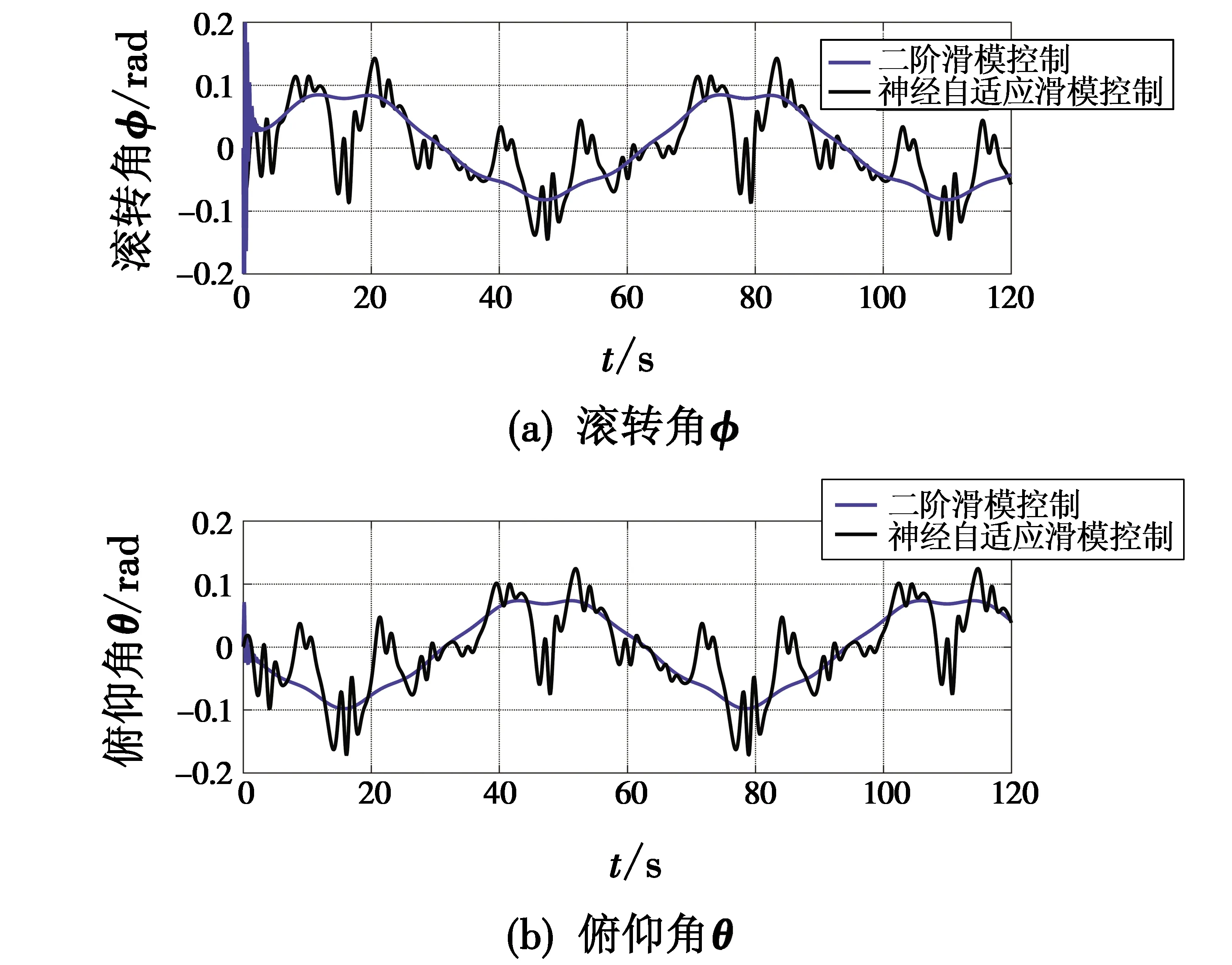
图7 滚转角φ和俯仰角θFig.7 The roll angle φ and the pitch angle θ

从图5、图6展现的跟踪轨迹来看，当存在系统模型不确定及外界连续干扰时，文献[16]的二阶滑模控制方案无法完成有效跟踪，各个通道都出现了明显波动，尤其是偏航通道，出现了较大的超调。图7中滚转角和俯仰角的变化过程，也印证了位置(x,y)通道出现的波动。而本文所提的神经自适应滑模控制方案却能够保证飞行器较好地按照预设期望轨迹进行飞行，表明在该控制器下，无人机系统具有较强的鲁棒性。