基于BP神经网络改进遗传算法的导弹总体参数快速优化方法

胥涯杰， 鲜 勇， 李邦杰

(火箭军工程大学作战保障学院，西安 710000)

0 引言

在确定导弹总体参数的过程中，在满足任务需求的条件下，需要对导弹的发动机质量、飞行程序角等进行设计，各参数的协同优化对提升武器性能和确保任务可行性具有重大意义[1]。由于优化理论的逐渐完善，导弹总体参数设计方法也不断成熟，其中,文献[2-4]利用多学科优化思想对导弹进行设计与优化，该思想对由多个复杂系统构成的总体设计工作有很好的指导作用，但是多学科优化设计方法复杂，而且还有在导弹概念阶段使用困难的问题；周伟等[5]利用改进粒子群、吴春晖等[6]采取改进多目标布谷鸟以及陈江宁等[7]将遗传算法与Powell算法组合,他们均利用优化搜索算法对此类多参数优化问题进行求解，这类数值优化算法及其改进方法具有概念清晰、设计灵活的特点，能在一定程度上简化设计难度，但要得到满足约束的可行解，必须通过设置大量迭代的环节实现，因此存在设计效率不高的缺点。

由于遗传算法在多参数优化中具有较好的并行搜索和全局搜索能力[8-9]，通常被应用于多参数优化问题。文献[10]阐述了遗传算法在飞航导弹设计上具有处理复杂非线性问题的优点，但遗传算法需要对每一代种群中所有个体都进行适应度的计算，而导弹总体设计中的适应度函数往往比较复杂，因此遗传算法的搜索效率较低。为了提高设计效率，本文在用遗传算法的寻优过程中，将训练好的网络模型代替传统弹道积分的过程，借此计算各组参数下的适应度，提高了遗传算法的计算效率。

1 导弹总体参数设计模型

设计目标是通过对飞行程序角参数的调整，寻找满足700 km射程下的最小发动机质量。

1.1 质量计算模型

本文中的质量按照一级导弹模型进行估算，导弹总质量M由有效载荷Ma和发动机质量Mb组成，即

M=Ma+Mb。

(1)

发动机质量Mb又由推进剂质量MT和结构质量MJ构成，即

MT=Mb×l

(2)

式中，l是发动机的装填比系数。

1.2 发动机模型

发动机真空额定推力为

P0=M×g0×xpm

(3)

式中：g0是地表重力加速度；xpm是发动机的推重比常数。

秒耗量为

(4)

式中，Isp 0是发动机真空比冲。

1.3 弹道模型

为了方便研究，将地球简化为静止的匀质圆球体，且导弹只在射面内运动。大气环境采用美国1976大气模型。

基于以上假设，导弹的质心运动模型为

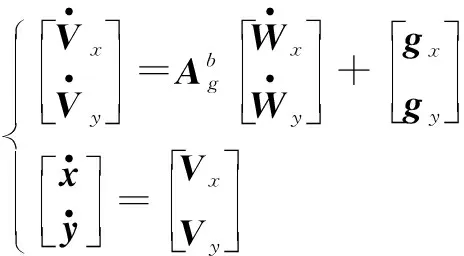
(5)

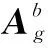
(6)

式中，φ为导弹俯仰角。

(7)

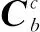
(8)

式中，α为导弹攻角。

式(7)中，X，Y分别为阻力和升力

(9)

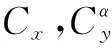
(10)

式中，P是当前发动机的实际推力

P=0.995×(P0+SaPk)

(11)

式中：0.995为考虑控制力机构及控制损失后的推力比率；Pk为导弹飞行高度处的大气压强；Sa为发动机喷管出口截面积。

式(5)中，gx，gy表达式为

(12)

式中，R为当前地心矢径

(13)

由于弹道导弹在发动机关机之后，自由段仅受地球引力，再入段仅受地球引力和再入阻力，导弹落点仅与关机点时刻的运动状态有关，进而得到导弹发射点到落点的距离，即为导弹的射程。因此，需要通过对导弹在主动段中飞行程序角的设计得到在满足射程下的关机状态。

1.4 飞行程序角模型

1.4.1 垂直起飞段

垂直起飞段，φ=90°。垂直起飞时间由经验公式确定，即

(14)

1.4.2 亚音速程序转弯段

在亚音速程序转弯段

φ=α1(t)+θ

(15)

式中：α1=-4αmax1ea1(t1-t)(1-ea1(t1-t))，αmax1为该转弯段最大攻角的绝对值，考虑最大法向过载和姿态控制系统能力，其值小于5°，a1是控制转弯快慢的常数；θ为弹道倾角，根据当前飞行速度计算

(16)

亚音速程序转弯时间是从垂直起飞段结束时刻到导弹飞行马赫数达到0.8为止。

1.4.3 跨音速段

在跨音速段

φ=θ。

(17)

为了保持导弹在跨音速段的稳定，要求攻角为0°，跨音速段时间是从亚音速程序转弯段结束时刻到导弹飞行马赫数达到1为止。

1.4.4 第二次程序转弯段

在第二次程序转弯段

φ=α2(t)+θ

(18)

式中，α2=-4αmax2ea2(t3-t)(1-ea2(t3-t))。第二次程序转弯时间是从跨音速段结束时刻到发动机关机前5 s为止。

1.4.5 定程序飞行段

飞行程序角保持上一段不变，定程序飞行段时间是从第二次程序转弯段到发动机关机为止。

1.5 约束条件

考虑最大法向过载和姿态控制系统能力，αmax1和αmax2的最大值分别是5°和10°；考虑导弹结构的承受能力，要求主动段的最大法向过载小于0.1g。

2 优化设计

通过上文的飞行程序角模型研究发现，对飞行程序角的优化过程即是对a1，a2，αmax1和αmax2这4个参数的确定过程，在导弹发动机性能、有效载荷、结构参数确定的情况下，优化目的就是寻找满足射程条件下的最小发动机质量。

在寻找最优飞行程序角时使用遗传算法，寻找在固定质量下射程最远的最优飞行程序角；在寻找满足射程的最小质量时，其中一种方法是将质量放入遗传算法中作为其中一个变量，这种做法虽然寻找速度较快，但是由于遗传算法的局部搜索能力较差[11]，无法确定在每个质量下的飞行程序角参数遍历较为全面，无法保证充分地发挥该质量下导弹的性能，因此，在这种条件下得到的结果不能确定是最优的。如果想要实现对每个确定质量下的飞行程序角参数的充分试探，需要将质量从遗传算法中剥离开来，然后对每个确定质量下的飞行程序角用遗传算法寻优，再判断是否满足射程条件，满足则减小质量，不满足则增加质量，通过迭代计算达到要求下的最佳质量。

BP神经网络具有强大的非线性拟合能力[12],用训练好的神经网络代替遗传算法中计算适应度函数需要进行的弹道积分过程，这样将大大提高遗传算法的搜索效率。总体优化流程如图1所示。

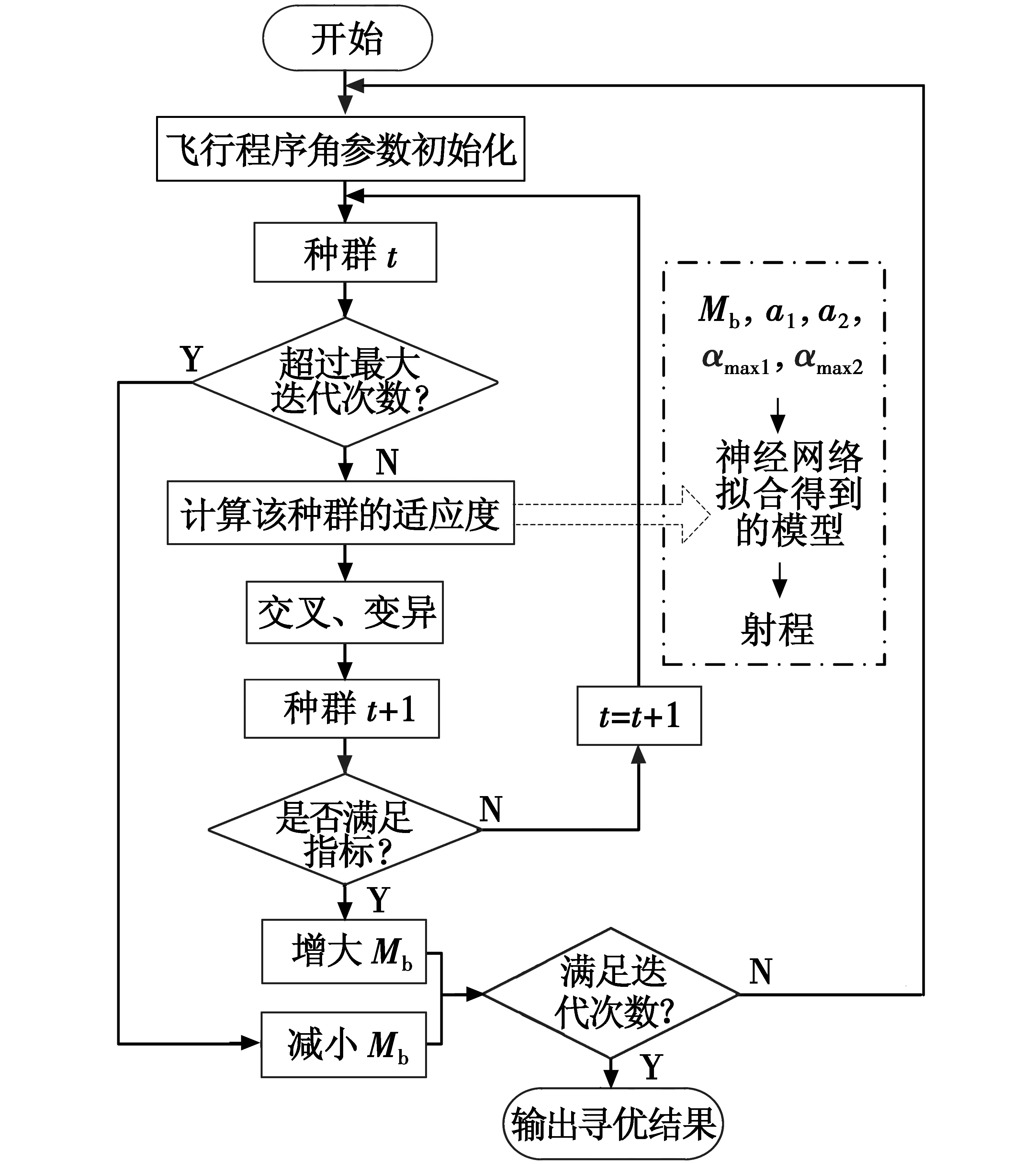
图1 优化流程Fig.1 The process of optimization

2.1 样本生成

将Mb，a1，a2，αmax1和αmax2作为神经网络的输入，将射程作为神经网络的输出。根据实际条件与经验分析，令Mb在5000～10 000 kg范围，a1在0～1范围，a2在0～2范围，αmax1在0°～5°范围，αmax2在0°～10°范围，将这5个参数在各自区间内随机组合，通过弹道程序积分计算每种组合下的射程，构成15 000组标准样本。

2.2 神经网络结构

设置3个隐藏层，节点数分别为10，8，5，加上输入、输出参数分别是5和1，可以得到BP神经网络的结构如图2所示。

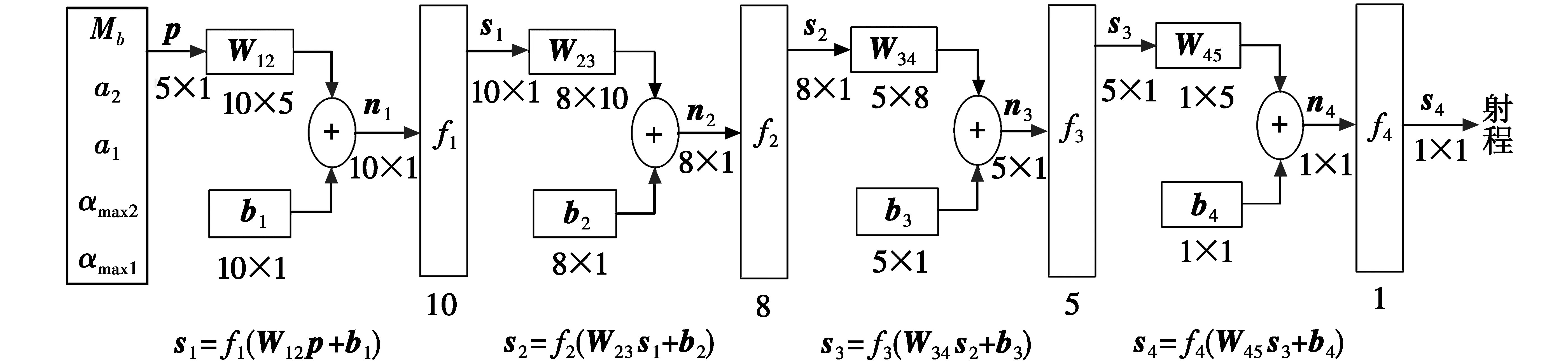
图2 神经网络结构Fig.2 Structure of neural network

2.3 神经网络训练

隐藏层均采用对数激活函数logsig，输出层采用线性激活函数purelin。将输入和输出数据进行归一化处理，保留归一化结构用于神经网络输出后的反归一化。

对这样的中型BP神经网络采用收敛速度最快的Levenberg-Marquardt算法[13]，训练时采用均方误差(Mean Squared Error，MSE)作为模型的损失函数，训练次数为2000。

2.4 优化质量

首先设置发动机质量的初值Mb=8000 kg，将遗传算法的种群数目设置为200，遗传代数设置为20，通过射程的快速计算判断在此演变过程中的射程是否满足要求，如果满足则减小发动机质量Mb=Mb/1.1，否则增加发动机的质量Mb=Mb×1.05，直至找到刚好满足射程指标的发动机质量。

寻找出的发动机质量以及此质量对应的飞行程序角参数就是总体参数的优化结果。

3 实验结果与分析

3.1 神经网络拟合效果

对弹道拟合的训练过程中训练误差收敛情况如图3所示。

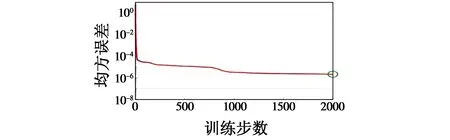
图3 误差收敛速度Fig.3 Convergence speed of error

使用600个标准样本对模型进行测试，其模型的测试误差结果如图4所示。

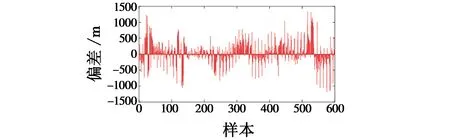
图4 测试误差Fig.4 Test error

测试误差的平均误差为270.999 5 m，标准差为259.419 9 m，最大误差为1 327.644 3 m。

在该总体参数的设计过程中，主要是判断射程能否达到指标，计算过程中达到千米级的精度即可，因此这样的测试结果是满足要求的。

3.2 参数寻优结果

为观察在不同参数下的弹道特性，选取在参数为Mb=6 626.59 kg，αmax1=3.720°，αmax2=8.600°，a1=0.253，a2=0.026条件下与寻找得到的最优参数下的弹道进行对比。图5是两者的飞行程序角变化对比，图6是两者飞行弹道的对比。通过对比发现，飞行程序所控制的导弹转弯角度的大小和快慢对射程的影响十分明显。

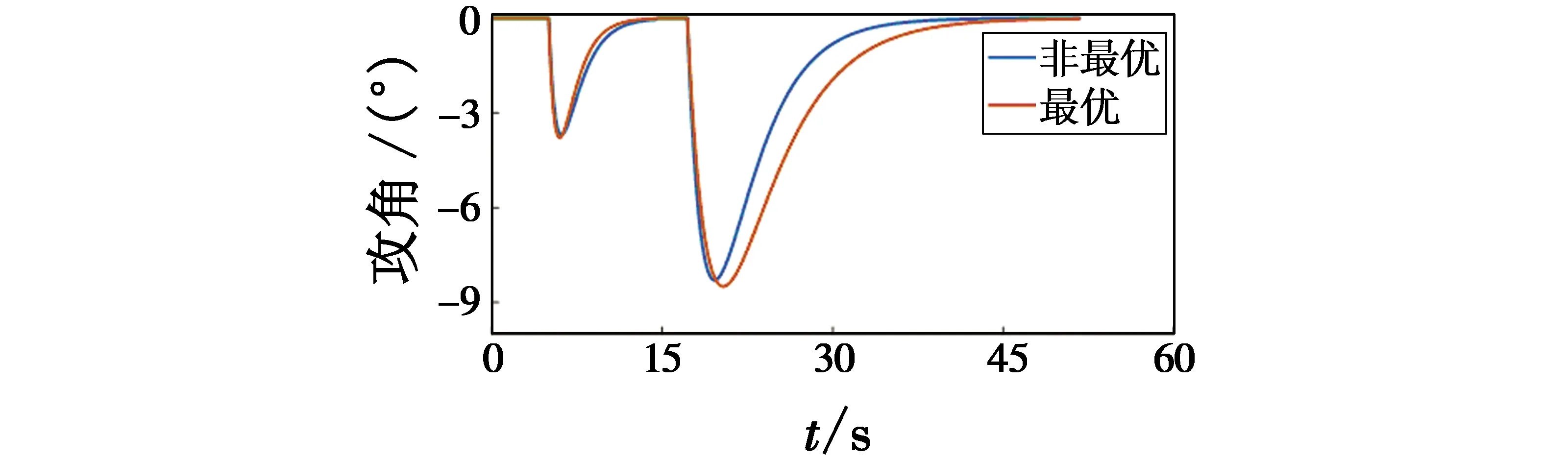
图5 时间-攻角Fig.5 Time vs angle of attack

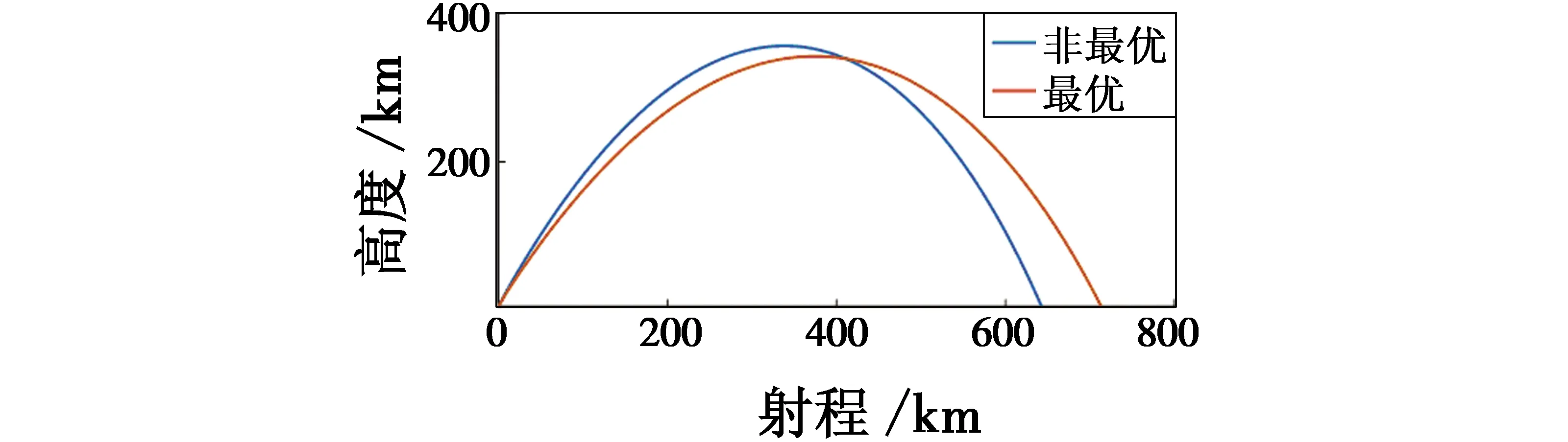
图6 射程-高度Fig.6 Range vs height

BP神经网络对弹道射程计算过程拟合完成后，大大降低了计算的复杂度。通过对比，在单个i7-9750H CPU(2.60 GHz)下，给定同样初值计算100次射程，弹道积分计算用时为13.492 s，用训练出来的BP神经网络代替遗传算法中适应度函数的弹道积分过程的方法用时仅为1.435 s，可以看出，改进后的遗传算法速度大大提高。

在种群规模为100、变异概率为0.05、遗传代数为200的情况下，通过遗传算法得到满足要求的最小质量为7 252.46 kg。

将训练出来的BP神经网络代替用弹道积分计算遗传算法中适应度函数的过程，得到的目标优化质量为6 626.59 kg。这说明将质量的优化从飞行程序角参数的寻找过程中剥离出来的方法，能有效减小遗传算法局部搜索能力弱带来的影响，提升算法的搜索能力。其优化过程部分数据记录如表1所示。

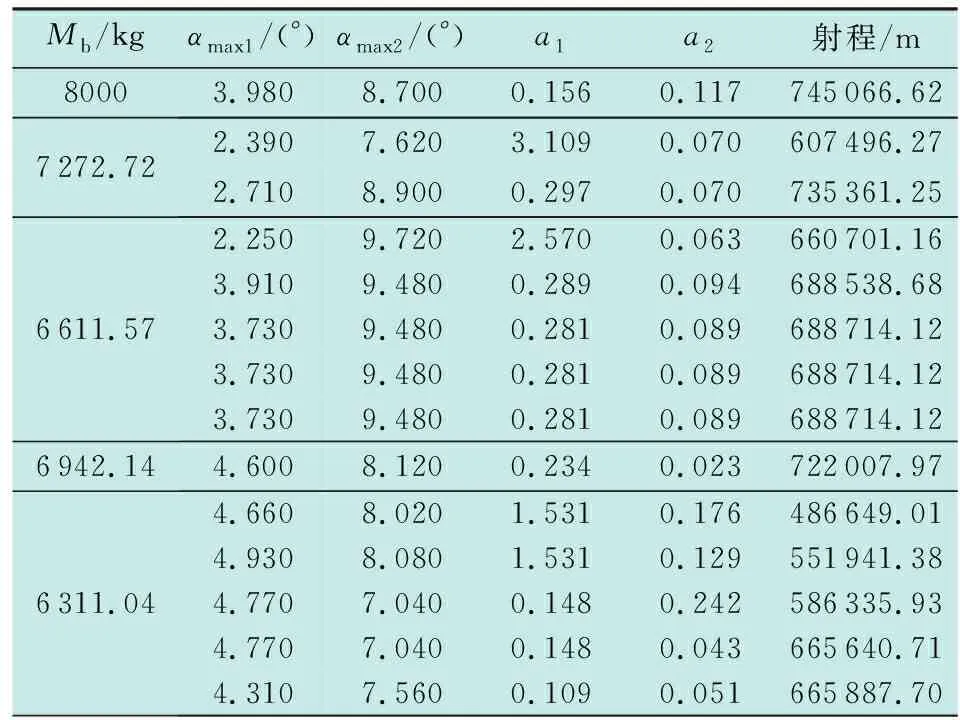
表1 优化过程数据Table 1 Data of the optimization process

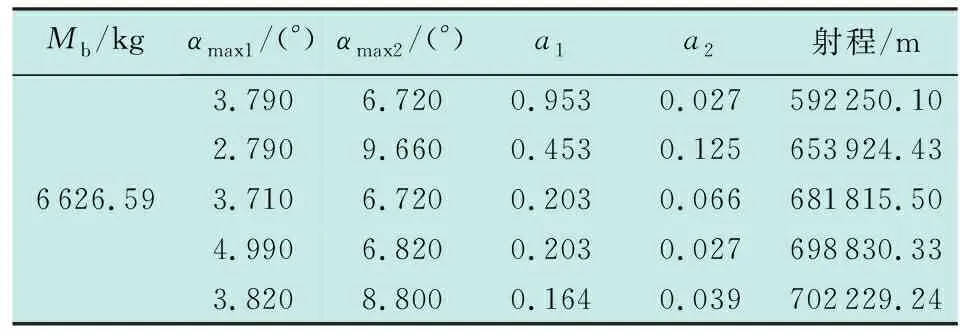
续表

最后选取Mb=6 626.59 kg,αmax1=3.820°,αmax2=8.800°，a1=0.164，a2=0.039作为满足射程700 km时的最小质量和对应的最佳飞行程序角参数。

4 结束语

本文利用BP神经网络强大的非线性拟合能力对弹道射程的计算进行拟合，能实现在给定质量和飞行程序角的条件下对射程进行快速计算，结合遗传算法，将此应用于适应度函数的计算。实验结果表明，此改进方法大大提高了遗传算法的搜索速度，为此类问题的解决提供了一种新的思路；同时，用迭代质量的方法降低了遗传算法局部搜索能力差带来的不良影响，对每个质量下的最大射程进行了充分挖掘，进一步优化了满足射程下的发动机质量。