基于多尺度建模与响应面法的55NiCrMoV7模具钢调质热处理工艺优化
2022-02-22赵继全曲周德武川石如星禹兴胜
赵继全,曲周德,武川,,石如星,禹兴胜
基于多尺度建模与响应面法的55NiCrMoV7模具钢调质热处理工艺优化
赵继全1,曲周德1,武川1,2,3,石如星2,3,禹兴胜2,3
(1. 天津职业技术师范大学 汽车模具智能制造国家地方联合工程实验室,天津 300222;2. 洛阳中重铸锻有限责任公司,河南 洛阳 471039;3. 中信重工机械股份有限公司,河南 洛阳 471039)
探究大型55NiCrMoV7模具钢锻件(1000 mm×1700 mm)调质热处理的最优工艺方案。建立大型55NiCrMoV7模具钢锻件的宏微观耦合的多尺度有限元模型,基于现场实验测试不同位置温度场和组织场的演化规律验证该模型。模拟研究此锻件在不同淬火与回火工艺下的应力分布、HRC硬度和屈服强度变化。以残余应力均方差、硬度和屈服强度为目标函数,建立淬、回火工艺参数与力学性能之间的回归模型。结合所建立的响应面模型分析与遗传算法,对该模型进行参量约束条件下的多目标优化。通过响应面模型分析得出最优工艺范围为:淬火温度为850~910 ℃,回火温度为400~550 ℃。多目标优化后得到Pareto最优解集:淬火907.4 ℃+回火443.1 ℃、淬火907.4 ℃+回火411.5 ℃、淬火903.4 ℃+回火485.1 ℃、淬火895.2 ℃+回火535.8 ℃和淬火892.1 ℃+回火507.1 ℃。建立的淬、回火温度对应力均方差、HRC硬度和屈服强度的回归模型,为大型55NiCrMoV7模具钢锻件调质热处理工艺优化提供了理论依据。
55NiCrMoV7模具钢;多目标优化;响应面法;遗传算法;多尺度模型
55NiCrMoV7模具钢作为一种热作模具钢,因其高温下具有良好的综合力学性能,被广泛应用于各种热作模具冲压制造领域[1]。目前,Jebaraj M等[2-3]研究了LN2和CO2冷却剂在55NiCrMoV7钢铣削中的作用,对55NiCrMoV7模具钢在低温环境下端铣加工表面完整性进行了探究。S. Hoja等[4]对55NiCrMoV7模具钢碳氮共渗处理的发展进行了研究。Weifang Zhang等[5]对大型模锻压力机上的模具座(由55NiCrMoV7钢制成)的脆性断裂行为进行了研究,指出在使用过程中产生的大尺寸碳化物是导致材料脆化和冲击韧性退化,进而导致模座脆性断裂的主要原因。在热处理工艺方面,张占平等[6-7]提出了55NiCrMoV7钢在复杂回火工艺条件下的动力学模型,建立了回火组织特征马氏体(211)峰物理半高宽-时间-回火温度的单一模型和分段模型。Mengting Fan等[8-9]对55NiCrMoV7钢进行了不同速率的淬火处理,并进行了600,620,650 ℃回火探究。禹兴胜等[10]模拟研究了65 t的55NiCrMoV7钢锭均质热处理过程中宏观偏析扩散规律,得出铬元素偏析是影响钢锭均匀化的主要因素,为制定均质热处理温度和时间提供了科学指导。
对大型钢锭进行恰当的调质热处理是提高其综合质量的关键,目前针对大型55NiCrMoV7模具钢锻件的调质工艺优化还鲜有报道[11]。因此文中将对55NiCrMoV7钢大型锻件进行调质工艺优化的探究,以改善其力学性能。为了得到调质工艺与力学性能之间的关系,文中拟采用响应面法建立响应面模型,并利用Matlab遗传算法工具箱进行多目标优化,相关研究结论为大型锻件热处理工艺的优化提供了理论依据和科学指导。
1 材料与实验
实验采用55NiCrMoV7钢锭锻制成规格为1000 mm×1700 mm的棒料,质量为10 625 kg,具体化学成分如表1所示。
实验热处理流程:对55NiCrMoV7模具钢进行890 ℃×10 h退火+740 ℃×24 h高温回火的锻后热处理工艺,以消除内应力,改善材料内部组织,为调质热处理做好组织准备,在锻后热处理过程中每隔7 min记录一次温度变化。调质热处理工艺采用860 ℃×16 h淬火+560 ℃×40 h回火,并对锻件进行金相组织观察、硬度及屈服强度测试,为大型55NiCrMoV7模具钢锻件的模型验证提供基础。
模拟调质热处理工艺可提供大量数据支撑,避免了纯实验所带来的巨大工作量,提高了工作效率。其工艺流程如下:≤200 ℃起温加热至淬火温度(790~ 910 ℃)后,空气预冷3 min+油冷200 min+上下串动10 min,淬火前油温≤60 ℃,回火(100~650 ℃)并出炉空冷至室温。控制升温速度为60 ℃/h,且采用阶梯加热的方式,具体调质工艺如图1所示。在模拟调质热处理结果中提取残余应力值、HRC硬度和屈服强度值,并计算出残余应力的均方差,以衡量残余应力在大型锻件内部分布的均匀性。
表1 实验材料55NiCrMoV7钢化学成分(质量分数)

Tab.1 Chemical component of 55NiCrMoV7 steel (mass fraction) %
2 模型的建立
2.1 大型55NiCrMoV7钢调质热处理的多尺度模型
基于DEFORM对材料构建的模型如图2所示,网格划分以六面体为主,边角处采用四面体网格细化局部特征,热处理过程中选用第3类边界条件,试件与外部环境通过热对流和热辐射进行热交换,空淬取恒温25 ℃,油冷取恒温50 ℃,考虑到试件的受热情况,升温阶段热交换系数设为0.1,降温阶段的换热系数通过实验测得,从试样心部到表层均匀选取32个点以提取残余应力值。
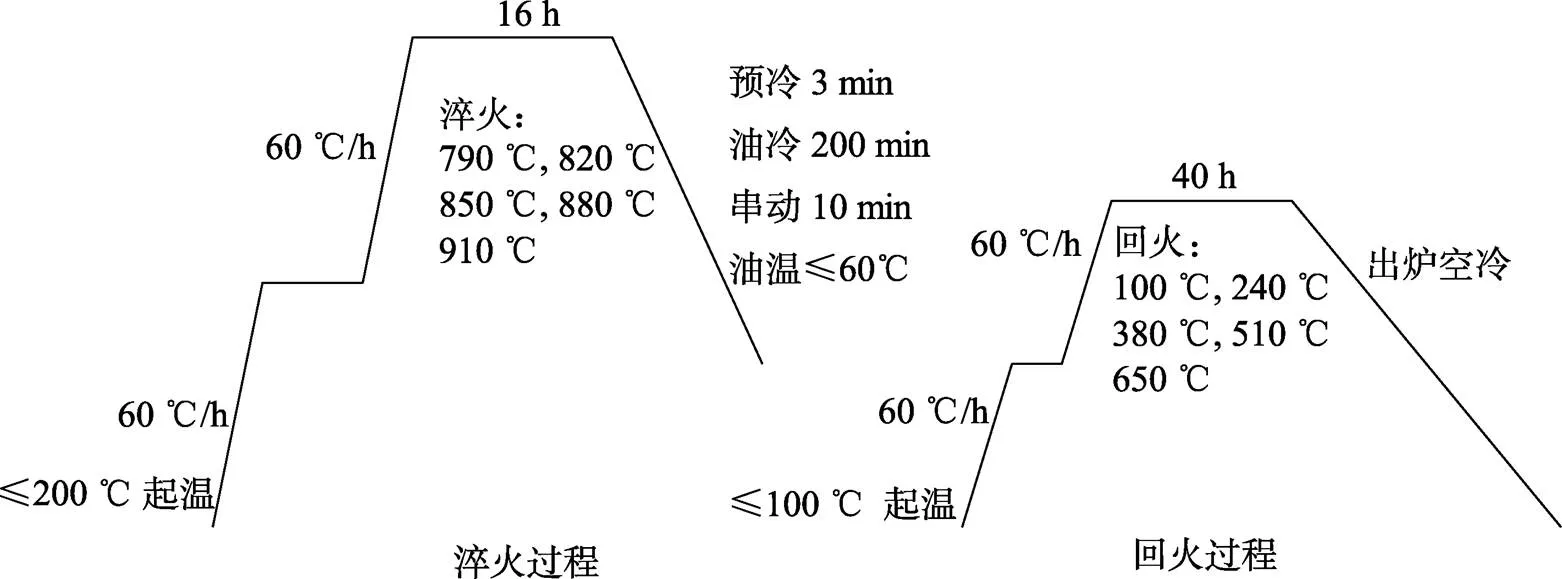
图1 模拟调质工艺流程
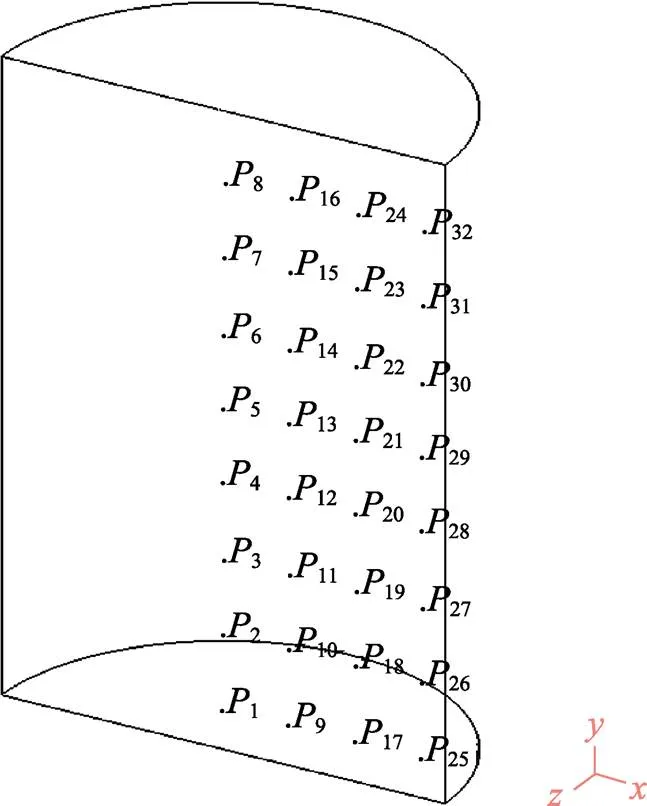
图2 55NiCrMoV7钢模型的建立
2.2 有限元模型的验证
2.2.1 温度场验证
为了验证有限元模型的可靠性,在锻后热处理过程中采用热电偶对55NiCrMoV7模具钢进行了温度测量,如图3a和3b所示,在55NiCrMoV7模具钢的外部至内部均匀选取了11个测温点,温度数据每间隔7 min提取一次,选取①和⑪位置的提取温度与同步模拟温度数据进行对比,结果如图4所示,可以看到在图4a中,①位置(即表层温度)模拟表面温度曲线与实测温度曲线基本重合,这证明了选取的网格划分方式以及热交换方式的正确性。在⑪位置(即心部温度)差别最大,如图4b所示,这是由锻件体积过于庞大以及在实际测温中不可避免的操作误差导致,但这些误差都在合理的范围之内,综合考量该模型具有一定的可靠性。

图3 不同部位温度测量
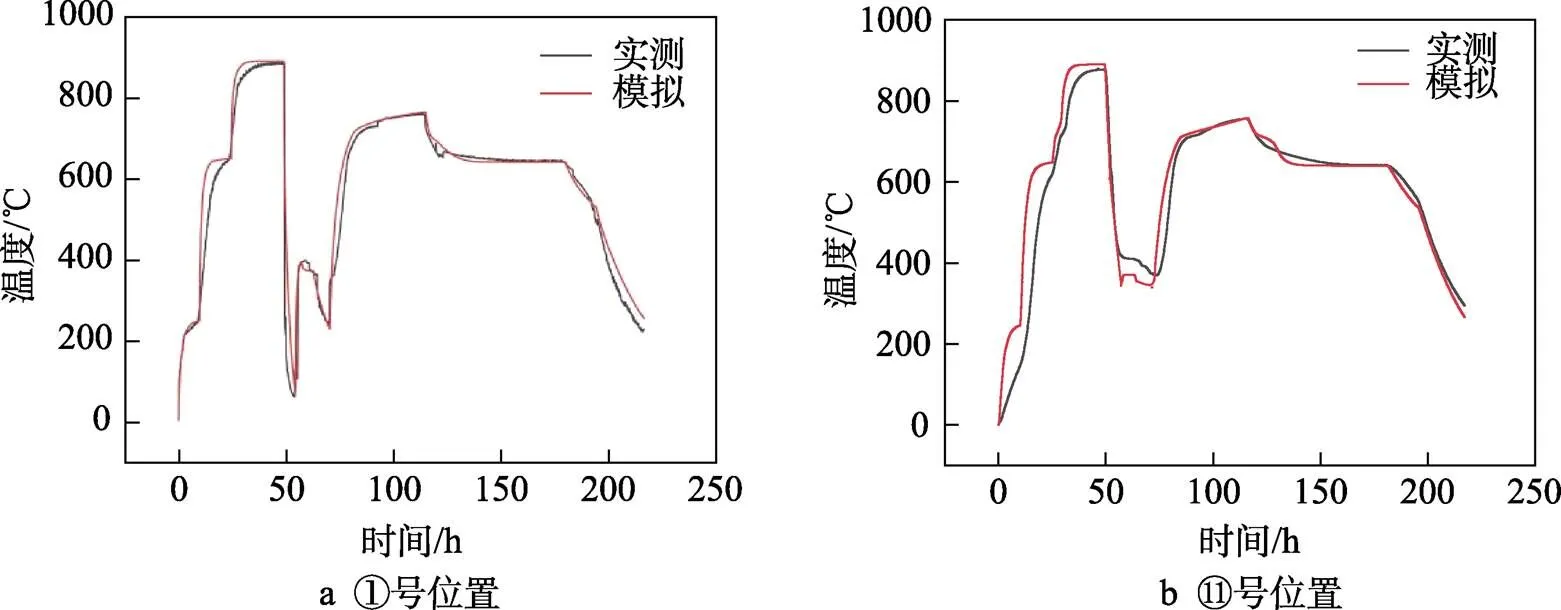
图4 模拟温度与实际温度对比
2.2.2 微观组织
55NiCrMoV7模具钢同步调质热处理模拟结果如图5所示,在热处理过程中棒料边角处吸热、散热能力较强,温度变化较快,故马氏体组织集中在棒料两端的边角处,如图5c所示,体积分数最大为23.9%。棒料内部在高温回火的条件下,渗碳体以颗粒状分布于铁素体的基体上,呈现粒状珠光体组织,由图5a可以看出珠光体在体积分数最小处都达到了52.1%。由图5b可以看出贝氏体主要分布在棒料的外层,体积分数占到了30.7%。综上分析可知,整个棒料的组织成分分布与温度场变化表现一致,这进一步印证了模型的可靠性。
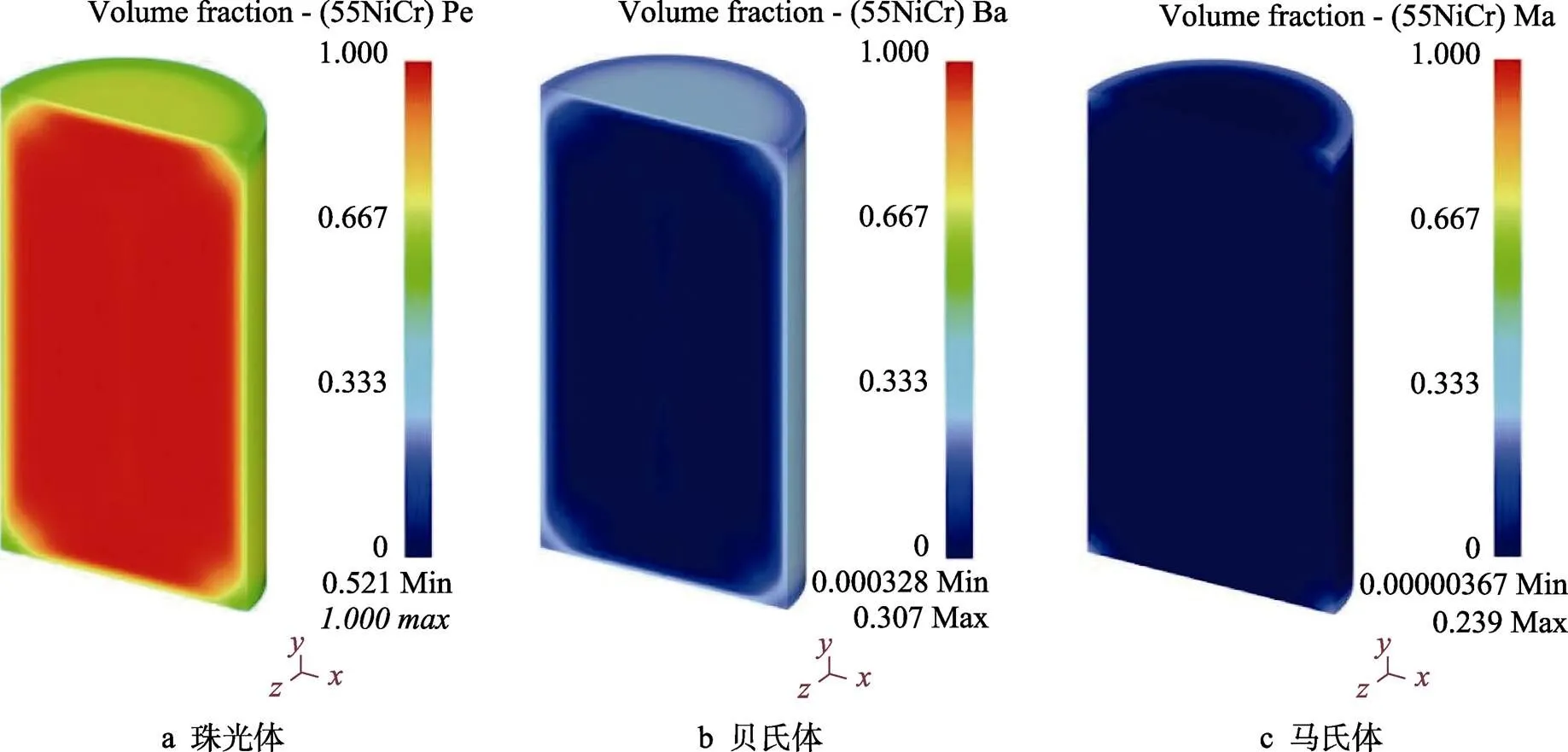
图5 模拟调质55NiCrMoV7钢组织分布
对调质热处理后的55NiCrMoV7模具钢棒料取样进行金相组织观察,如图6所示,1号取样位置距端部50 mm,2号取样位置距端部425 mm(即1/4处),3号取样位置为棒料正中间,4号取样位置为棒料另一端且距端部50 mm处,所有取样宽度均为20 mm。每个取样位置由表及里分别取样并编号为:1-1,1-2,1-3,2-1,2-2,2-3,3-1,3-2,3-3,4-1,4-2,4-3,取样位置详见图6。
55NiCrMoV7钢棒料表层组织成分变化如图7a,d,g所示。由图7a可以看出,基体以珠光体为主,针状马氏体组织附着在其表面,极少量的粒状碳化物存在于马氏体之间,大量碳化物都溶入了马氏体之中,且马氏体组织明显多于图7d和图7g。在图7d中贝氏体组织显现,与马氏体组织夹杂分布,组织间碳化物增多且分布杂乱。图7g中几乎看不到马氏体的踪迹,组织以珠光体和贝氏体为主,粒状碳化物较图7d略小。随着向棒料内部推进组织成分的变化,如图7b,e,h所示,从图7b可以看出,部分碳化物在马氏体中析出,马氏体组织含量减少。图7e中马氏体消失,碳化物不断长大。在图7h中碳化物体积略有减小,且趋于均匀化分布。棒料心部组织变化如图7c,f,i所示,可以看到心部共同特点是碳化物颗粒比较细小且分布均匀,其中图7i棒料中心部位,碳化物颗粒细小而弥散均匀分布于铁素体基体上,呈现为粒状珠光体组织,该部位组织均匀性最好。图7j—l取样位置与图7a—c取样位置呈对称分布,观察其组织分布可以发现二者一致,故证明了该实验结果的正确性。模拟组织分布与实验结果观察一致,也证明了大锻件55NiCrMoV7钢有限元模型的可靠性。
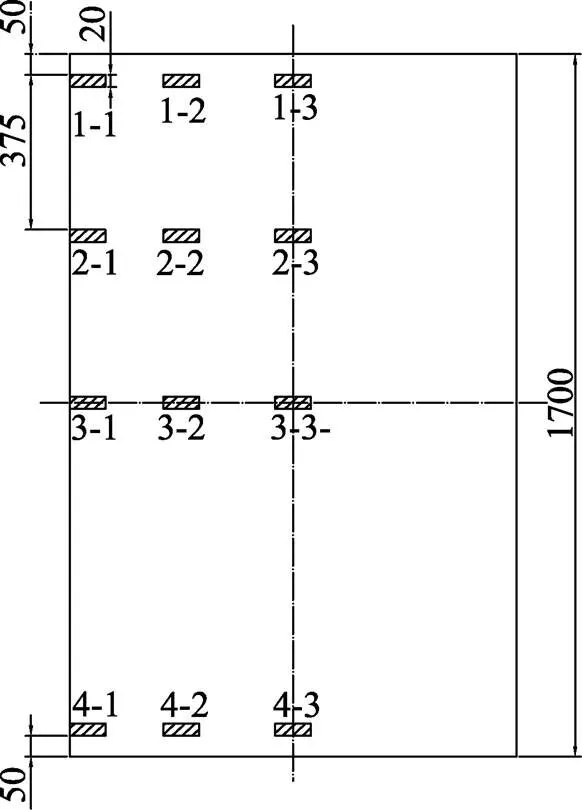
图6 金相取样部位示意
3 结果与讨论
3.1 淬火温度影响
3.1.1 残余应力变化
790~910 ℃不同温度淬火+510 ℃回火模拟后的残余应力分布情况如图8所示,从图8a—c可以看出,残余应力最小区域主要集中在棒料中心两端且成对称分布,棒料侧面应力较小区域随着淬火温度的增加及淬透性的增强,而逐渐消失,这符合热应力产生规律[12]。从图8d可知,随着淬火温度的升高,残余应力最大值略微提高,且不超过800 MPa,最小值略有浮动。综上所述,在模拟过程中随着淬火温度的上升,虽然残余应力最小区域不断缩小但高低应力区域划分明显,故淬火温度对改善残余应力分布影响较小。

图7 55NiCrMoV7钢调质后不同部位金相组织
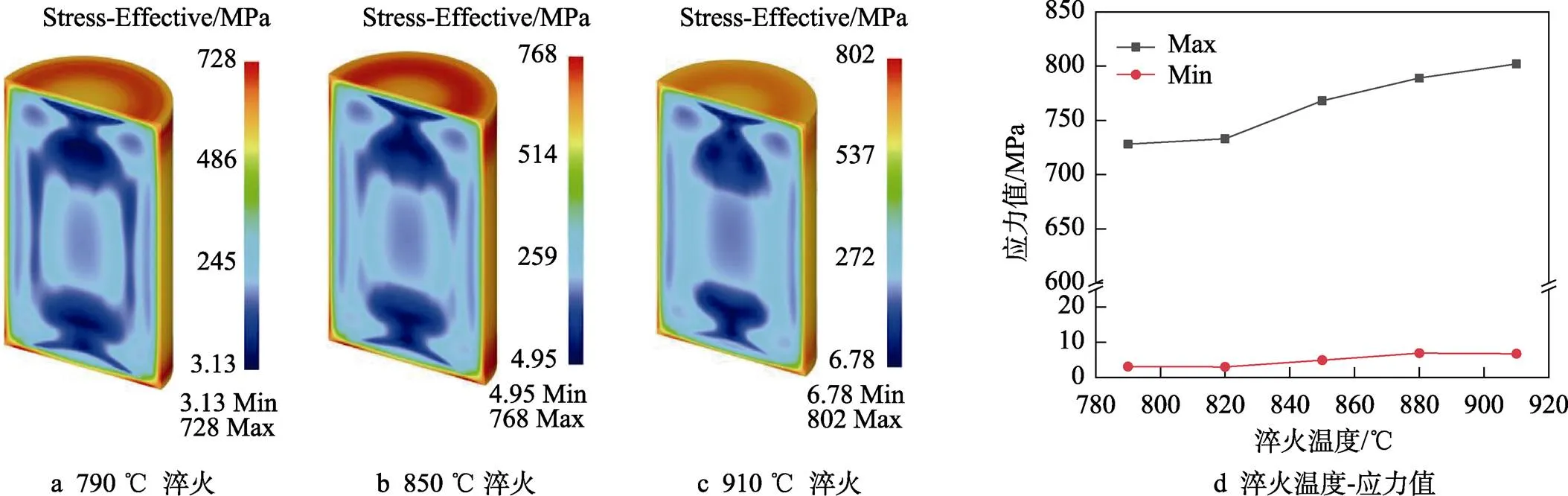
图8 不同温度淬火+510 ℃回火应力分布
3.1.2 模拟硬度和屈服强度变化
由图9a可知,790 ℃淬火时硬度仅为42.8HRC,但在820 ℃及以上淬火后,硬度均大于44HRC,其中820 ℃淬火硬度最大为45.1HRC,在860 ℃淬火后实验测得硬度为44.7HRC,与预测值接近,故不同淬火温度对硬度的影响很小。屈服强度随淬火温度变化如图9b所示,在淬火温度为880 ℃时,屈服强度最大为1335 MPa,860 ℃淬火实验值为1310 MPa。综上所述,为了兼顾材料硬度和屈服强度,淬火温度应保持在850 ℃以上。
3.2 回火温度影响
3.2.1 残余应力变化
850 ℃淬火+不同温度回火模拟后的残余应力分布如图10所示,由图10a—c可以看出,残余应力最大区域总是集中在棒料表层,这是由于表层温度变化较快,塑性变形不均匀而产生热应力,残余应力最小区域呈杯状分布在棒料两端及侧面,且随着回火温度的升高侧面低应力区域逐渐发散最后消失,端部杯状区域也有所减小,高、低应力区划分愈发明显。其中380 ℃回火后,如图10b所示,低应力区域发散明显,高低应力区域界线模糊,应力均匀性较好。由图10d可以看出,随着回火温度的升高,残余应力最大值不断降低,最低可达476 MPa。综上所述,回火温度对残余应力分布影响较大,其中380 ℃回火可以有效提高大型锻件残余应力分布均匀性。
3.2.2 模拟硬度和屈服强度变化
由上述可知,回火温度的升高有利于消除残余应力,提高应力分布均匀性,但是过高的回火温度会造成其他力学性能下降,如图11所示,由图11a可知,当回火温度高于510 ℃时,材料的硬度会急剧下降,这是因为500 ℃以上高温回火,碳化物不断在马氏体中析出,导致马氏体的含碳量大大降低,硬度呈现断崖式下跌[13]。如图11b所示,屈服强度在380 ℃时达到最大值1450 MPa,此后回火温度越高,屈服强度下降越明显,这与回火过程中马氏体组织软化有关。在560 ℃回火实验后测得硬度为41.8HRC,屈服强度为1130 MPa,预测值与实验值在误差允许的范围之内。

图9 淬火温度对硬度和屈服强度的影响
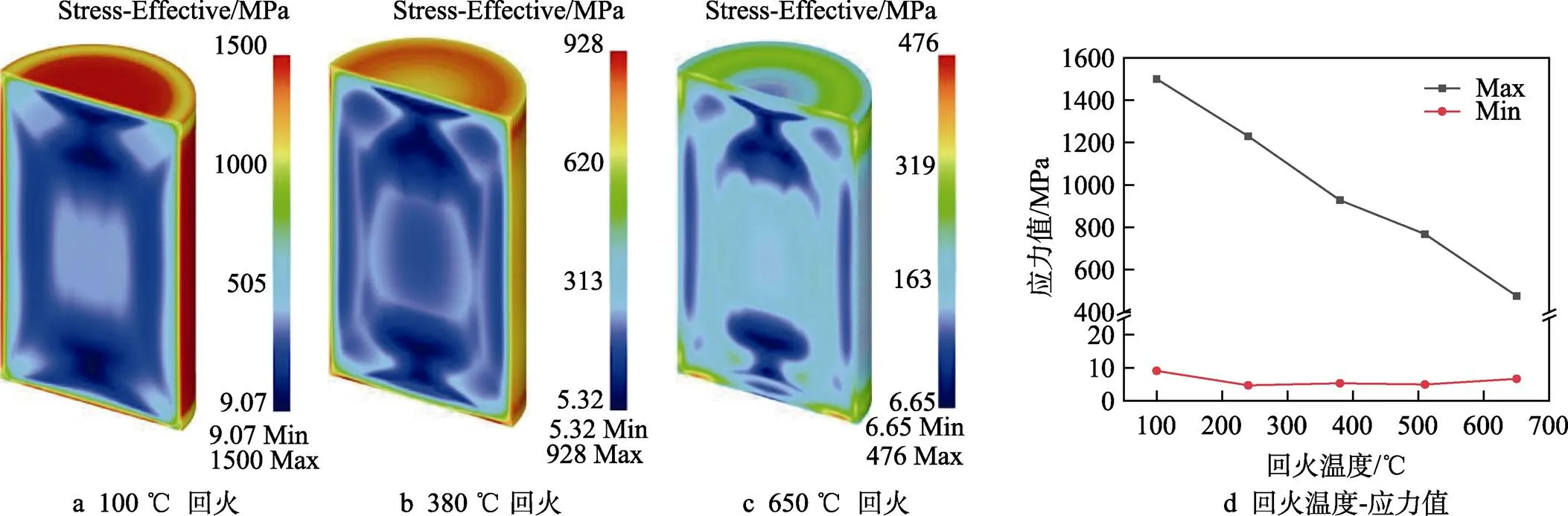
图10 850 ℃淬火不同温度回火应力分布
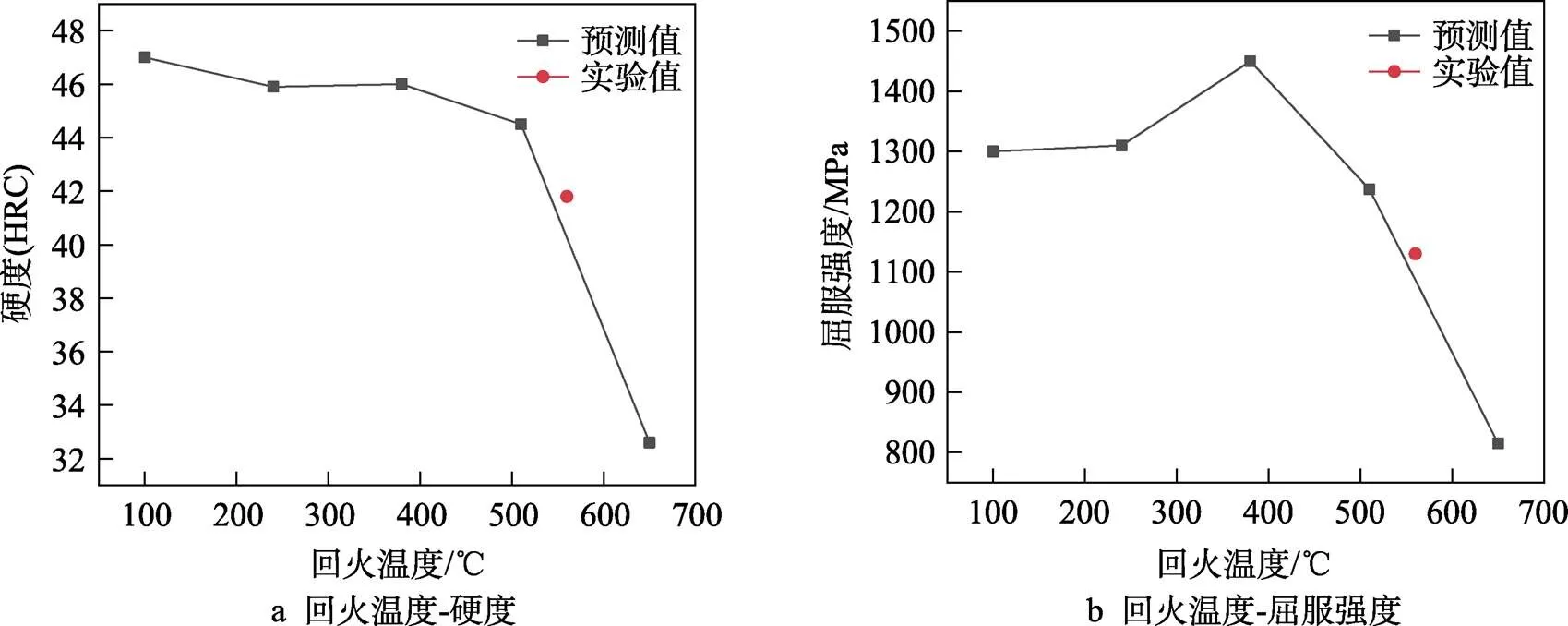
图11 回火温度对硬度和屈服强度的影响
3.3 热处理工艺优化
3.3.1 响应面模型的建立
基于调质模拟实验设计及结果(如表2所示)对调质热处理工艺进行残余应力分布、硬度和屈服强度的多目标优化。实验采用二因素、五水平中心组合[14](Central Composite Design)的设计方法,获得了调质工艺与力学性能的响应关系,即将淬火温度和回火温度作为自变量,应力均方差洛氏硬度和屈服强度s作为因变量,根据表2中模拟数据构建函数模型,经拟合得到回归方程如下:
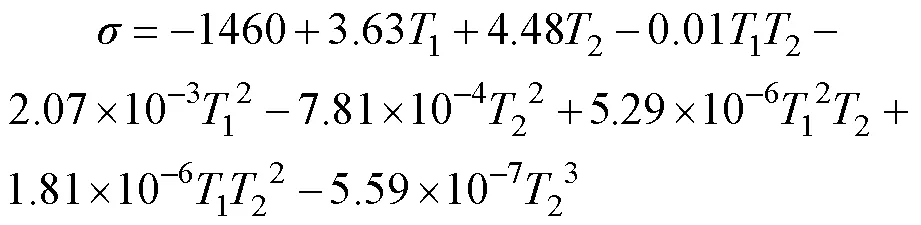
(2)
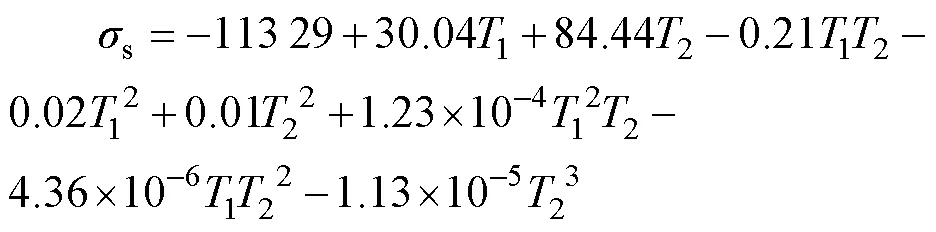
式中:1为淬火温度(℃);2为回火温度(℃)。
3.3.2 响应面模型分析
根据调质模拟实验结果绘制淬火温度和回火温度对应力均方差、硬度和屈服强度的3D响应曲面模型,如图12所示。在400~550 ℃区间回火时,850~ 910 ℃的淬火温度会使应力均方差略低,即锻件应力分布均匀性较好。同时由图13—14可知,在850~ 910 ℃随着淬火温度的升高,硬度和屈服强度的值也在增大,因此淬火温度应控制在850~910 ℃。由图12可以看出400 ℃以下回火,会导致残余应力均方差的值大大增加,即大型锻件的应力分布均匀性变差,随着回火温度的升高,应力均方差值逐渐减小,有利于提高残余应力分布的均匀性,因此应控制回火温度不低于400 ℃。但是回火温度太高会导致材料的硬度和屈服强度大幅降低,如图13所示,超过550 ℃的高温回火,随着回火温度的升高,会使材料的硬度急剧下降,同时对比图14可知,屈服强度的变化趋势与硬度变化基本一致。因此,为了保证各项指标的合格性,回火温度应控制在400~550 ℃。
表2 调质模拟实验设计及结果
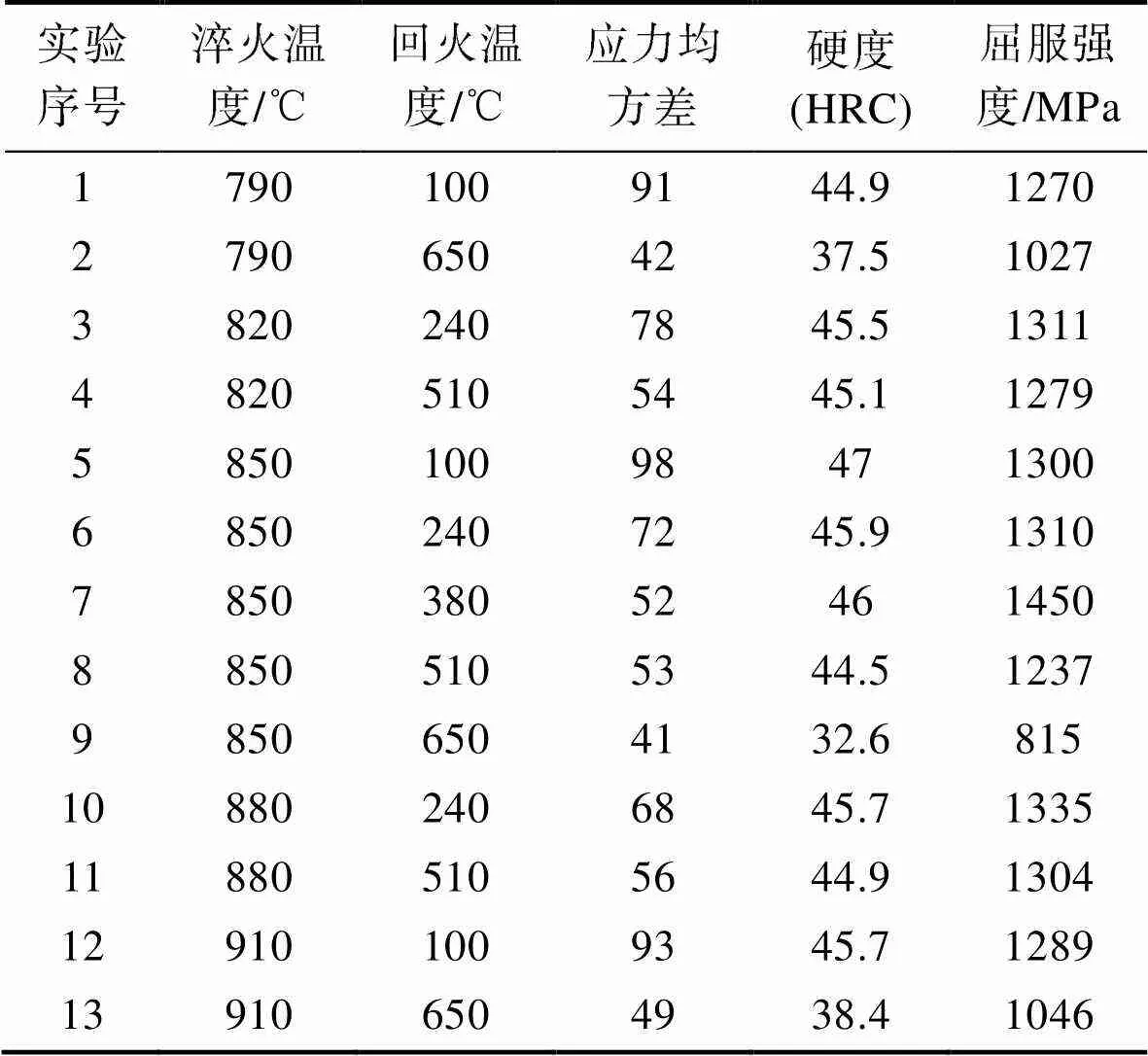
Tab.2 Experiment design and results of simulated tempering and quenching
3.3.3 基于遗传算法的多目标优化
3D响应曲面模型可以直观反映出调质工艺对某一性能指标的影响规律,但不能对应力均方差、硬度和屈服强度3个目标协调求解。为了获得匹配性较好的调质工艺,文中基于Matlab遗传算法工具箱(GA工具箱)进一步对大型锻件55NiCrMoV7模具钢的力
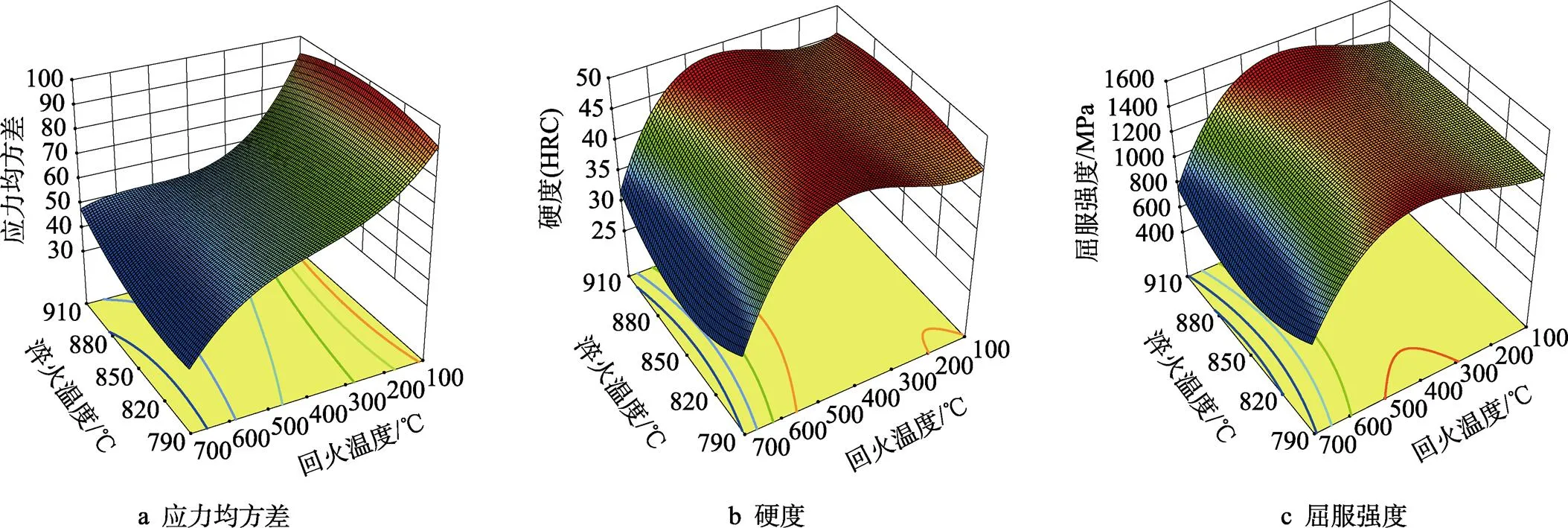
图12 3D响应曲面模型
学性能进行多目标优化。在多目标的优化过程中,所有的目标函数必须同时被最大或最小化,GA工具箱默认函数值越小越优[15]。故多目标函数可表示为:
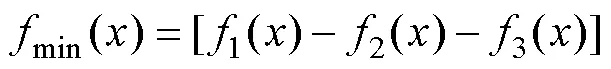
式中:1()为应力均方差模型;2()为硬度模型;3()为屈服强度模型s。根据式(4)建立优化模型,设置初始种群为50,最优个体系数为0.3,进化代数为200,交叉概率为0.95,变异概率为0.05,运行结果如表3所示。
表3 多目标优化模型运行结果
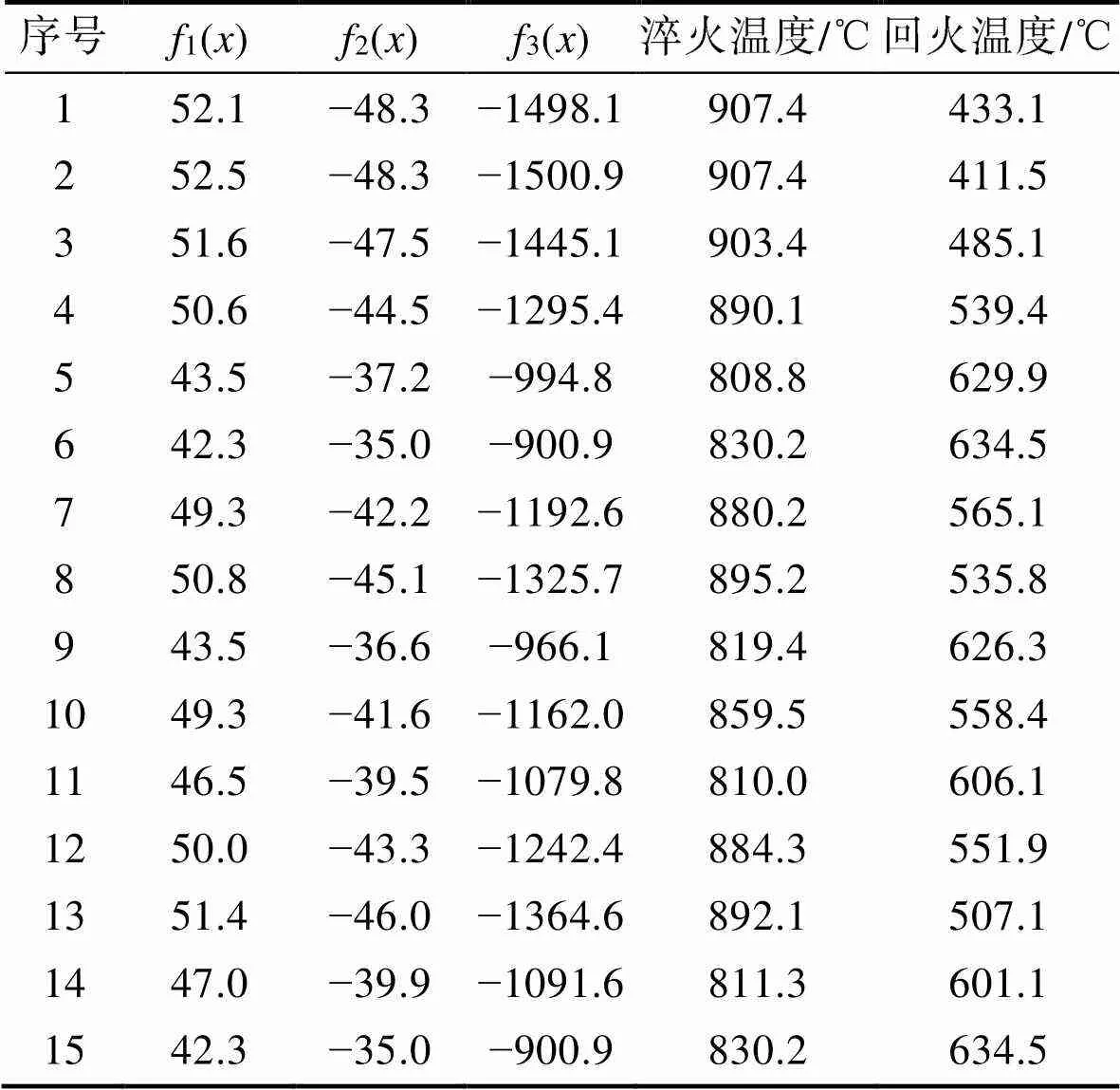
Tab.3 Running results of multi-objective optimization model
通过多目标优化模型运行结果可知,并不存在同时使应力均方差最小、硬度和屈服强度最大的解,但是可以找到符合各项指标要求的解。要求残余应力均方差不大于60,硬度不低于45HRC,屈服强度不小于1300 MPa,如图13所示,最终符合综合力学性能的点为:1,2,3,8,13。对应的工艺参数分别为:淬火907.4 ℃+回火443.1 ℃、淬火907.4 ℃+回火411.5 ℃、淬火903.4 ℃+回火485.1 ℃、淬火895.2 ℃+回火535.8 ℃和淬火892.1 ℃+回火507.1 ℃。在Pareto最优解求解的过程中,每次计算过程进行的交叉进化和变异不同,导致Pareto最优解求解运行的结果不同,但每次结果的改变都是通过牺牲其他目标函数实现的,每个Pareto最优解都同时满足多目标优化问题[16]。这就意味着以上5组工艺属于平行关系,无优劣之分。

图13 多目标优化Pareto最优解
4 结语
1)建立了大型55NiCrMoV7模具钢锻件的有限元模型,并通过实验测温和微观组织分析验证了该模型。
2)建立了淬、回火温度对应力均方差、HRC硬度和屈服强度的回归模型。
3)确定最优工艺范围:淬火温度为880~910 ℃,回火温度为400~550 ℃。得到Pareto最优解集:淬火907.4 ℃+回火443.1 ℃、淬火907.4 ℃+回火411.5 ℃、淬火903.4 ℃+回火485.1 ℃、淬火895.2 ℃+回火535.8 ℃和淬火892.1 ℃+回火507.1 ℃。
[1] 史正良, 刘金龙. 热作模具钢的选择与应用[J]. 煤矿机械, 2007(12): 126-129.
SHI Zheng-liang, LIU Jin-long. Choice and Application of Hot Die Steels[J]. Coal Mine Machinery, 2007(12): 126-129.
[2] JEBARAJ M, PRADEEP K M, ANBURAJ R. Effect of LN2and CO2Coolants in Milling of 55NiCrMoV7 Steel[J]. Journal of Manufacturing Processes, 2020, 53: 318-327.
[3] JEBARAJ M, PRADEEP K M, YUVARAJ N, et al. Investigation of Surface Integrity in End Milling of 55NiCrMoV7 Die Steel under the Cryogenic Environments[J]. Machining Science and Technology, 2020, 24(3): 465-488.
[4] HOJA S, SKALECKI M G, KLÜMPER-WESTKAMP H, et al. Carbonitrieren von Warmarbeitsstählen[J]. HTM- Journal of Heat Treatment and Materials, 2017, 72(4): 187-198.
[5] ZHANG W, WANG H, ZHANG J, et al. Brittle Fracture Behaviors of Large Die Holders Used in Hot Die Forging[J]. Metals, 2017, 7(6): 198.
[6] 张占平, 齐育红, DELAGNES D, 等. 钢的回火时间-温度-硬度动力学关系[J]. 金属热处理学报, 2004(1): 41-45.
ZHANG Zhan-ping, QI Yu-hong, DELAGNES D, et al. Time-Temperature-Hardness Kinetics Relation of Tempering Steels[J]. Transactions of Materials and Heat Treatment, 2004(1): 41-45.
[7] 张占平, 齐育红, DELAGNES D, 等. 55NiCrMoV7钢的回火组织与性能[J]. 金属热处理, 2004(3): 27-31.
ZHANG Zhan-ping, QI Yu-hong, DELAGNES D, et al. Microstructures and Properties of the Tempered Steel 55NiCrMoV7[J]. Heat Treatment of Metals, 2004(3): 27-31.
[8] FAN Meng-ting, SUN Ming-yue, LI Dian-zhong. Effect of Microstructural Evolution on Mechanical Properties of 55NiCrMoV7 Steel[J]. Advanced Materials Research, 2011, 1334: 848-852.
[9] 樊梦婷, 孙明月, 李殿中. 大型压力机模座热处理过程模拟及工艺优化[J]. 材料工程, 2011(11): 44-50.
FAN Meng-ting, SUN Ming-yue, LI Dian-zhong. Simulation and Optimization of Heat Treatment Process for Large Press Die Holder[J]. Journal of Materials Engineering, 2011(11): 44-50.
[10] 禹兴胜, 武川, 李昌义, 等. 55NiCrMoV7钢锭均质化处理宏观偏析热扩散元胞自动机模拟研究[J]. 科技创新与应用, 2020(31): 18-19.
YU Xing-sheng, WU Chuan, LI Chang-yi, et al. Simulation of Macrosegregation Thermal Diffusion Cellular Automata for Homogenization of 55NiCrMoV7 Ingot[J]. Technology Innovation and Application, 2020(31): 18- 19.
[11] 赵继全, 曲周德, 禹兴胜, 等. 调质热处理对55NiCrMoV7模具钢组织与力学性能的影响[J]. 特殊钢, 2021, 42(4): 60-65.
ZHAO Ji-quan, QU Zhou-de, YU Xing-sheng, et al. Microstructure Evolution and Mechanical Properties Study of 55NiCrMoV7 Die Steel after Quenching and Tempering[J]. Special Steel, 2021, 42(4): 60-65.
[12] WU Chuan, MENG Qing-ling. Microstructural Evolution of a Steam Turbine Rotor Subjected to a Water Quenching Process: Numerical Simulation and Experimental Verification[J]. Advances in Manufacturing, 2019, 7(1): 84-104.
[13] 李爽, 时彦林, 杨晓彩, 等. 钼钨钒合金化热作模具钢高温回火组织演变[J]. 工程科学学报, 2020, 42(7): 902-911.
LI Shuang, SHI Yan-lin, YANG Xiao-cai, et al. Microstructural Evolution of Mo-W-V Alloyed Hot-Work Die Steel during High-Temperature Tempering[J]. Chinese Journal of Engineering, 2020, 42(7): 902-911.
[14] 肖瑞, 杨明, 黄朝文. 基于响应面法对211ZX新型高强铝合金固溶工艺的优化设计[J]. 稀有金属, 2019, 43(10): 1040-1046.
XIAO Rui, YANG Ming, HUANG Chao-wen. Optimal Design of 211ZX High Strength Aluminum Alloy Solid Solution Process Based on Response Surface Method[J]. Chinese Journal of Rare Metals, 2019, 43(10): 1040- 1046.
[15] PHAN-NGUYEN Huu. Multi-Objective Optimization in Titanium Powder Mixed Electrical Discharge Machining Process Parameters for Die Steels[J]. Alexandria Engineering Journal, 2020, 59(6): 4063-4079.
[16] 卢秋霞, 刘洁, 王志鹏. 铝合金板件自冲铆接性能的响应面-遗传算法优化[J]. 锻压技术, 2021(5): 57-63.
LU Qiu-xia, LIU Jie, WANG Zhi-peng. Optimization on Self-Piercing Riveted Performance of Aluminum Alloy Plate Part Based on Response Surface and Genetic Algorithm[J]. Forging & Stamping Technology, 2021(5): 57-63.
Optimization of Quenching and Tempering Heat Treatment Process for 55NiCrMoV7 Die Steel Based on Multi-Scale Modeling and Response Surface Methodology
ZHAO Ji-quan1, QU Zhou-de1, WU Chuan1,2,3, SHI Ru-xing2,3, YU Xing-sheng2,3
(1. National-local Joint Engineering Laboratory of Intelligent Manufacturing Oriented Automobile Die & Mould, Tianjin University of Technology and Education, Tianjin 300222, China; 2. Luoyang CITIC Casting and Forging Co., Ltd., Luoyang 471039, China; 3. CITIC Heavy Industries Co., Ltd., Luoyang 471039, China)
The work aims to investigate the optimal process scheme of quenching and tempering heat treatment of large 55NiCrMoV7 die steel forgings (1000 mm × 1700 mm). A multi-scale finite element model of macro-micro coupling for 55NiCrMoV7 die steel forgings was established to test the temperature field and microstructure field evolution at different locations based on field experiments and then the model was verified. The stress distribution, HRC hardness and yield strength of the forgings were simulated under different quenching and tempering processes. The regression model between the parameters of quenching and tempering and mechanical properties was established with the mean square error of residual stress, hardness and yield strength as the objective function. Combined with the response surface model analysis and genetic algorithm, the multi-objective optimization of the model under parameter constraints was carried out. According to the analysis of response surface model, the optimal process range was as follows: quenching temperature of 850~910 ℃, tempering temperature of 400~550 ℃. After multi-objective optimization, the optimal solution set of Pareto was obtained: quenching of 907.4 ℃+ tempering of 443.1 ℃, quenching of 907.4 ℃+ tempering of 411.5 ℃, quenching of 903.4 ℃+ tempering of 485.1 ℃, quenching of 895.2 ℃+ tempering of 535.8 ℃ and quenching of 892.1 ℃+ tempering of 507.1 ℃. The established regression model of quenching and tempering temperature on stress mean square error, HRC hardness and yield strength provides a theoretical basis for the optimization of quenching and tempering heat treatment process for large 55NiCrMoV7 die steel forgings.
55NiCrMoV7 die steel; multi-objective optimization; response surface method; genetic algorithm; multi-scale model
10.3969/j.issn.1674-6457.2022.02.012
TG316
A
1674-6457(2022)02-0074-09
2021-05-20
中国博士后第67批面上项目(2020M672309)
赵继全(1996—),男,硕士生,主要研究方向为模具钢热处理。
曲周德(1972—),男,博士,教授,主要研究方向为模具钢热处理。
