Q460高强钢柱在近爆荷载作用下的动力响应研究

2022-02-22张秀华张唯佳

振动与冲击 2022年3期

张秀华，张唯佳，张宇

(1. 东北林业大学土木工程学院，哈尔滨 150040; 2. 齐齐哈尔大学建筑与土木工程学院，黑龙江齐齐哈尔 161003)

钢结构具有轻质高强，塑性韧性好等特点被广泛应用在大跨结构、高层以及超高层结构中。钢柱是钢框架结构中重要的受力及传力构件，如果钢柱遭到爆炸冲击，可能导致局部构件失效造成建筑物连续倒塌，因此研究高强钢柱在爆炸荷载作用下的动力响应尤为重要。Yuen等[1-2]进行了许多钢板在不同规模爆炸荷载作用下的结构响应的试验研究，给出了钢板3种典型的爆炸破坏模式。周龙云等[3]数值模拟了H型钢柱在爆炸荷载作用下的水平位移和剩余承载力，提出了钢柱受损的判定依据并划分了损伤性等级。谢丽萍等[4]对钢框架结构的连续倒塌进行动力响应分析，提出结构角部区域构件设计应加强的建议。洪辉等[5]对一个8层钢框架结构在爆炸荷载作用下的损伤机理进行数值分析，提出框架梁梁端容易发生剪切破坏。李国强等[6]研究了爆炸作用下钢柱的破坏时间及残余承载力对钢框架连续倒塌的影响。张秀华等[7-10]对爆炸荷载作用下钢框架结构、钢柱、钢梁、压型钢板组合楼板等进行了研究，得出其在爆炸荷载作用下的破坏模式和影响动力响应的主要因素；并利用大型核爆炸模爆器进行乙炔-空气可燃气体爆炸试验研究，探索乙炔-空气可燃气体作为爆炸源对结构抗爆试验的可行性[11]。杨涛春等[12]对钢柱不同位置测点的冲击波曲线进行分析，给出工字型钢柱上爆炸作用的确定方法。曲艳东等[13-14]对爆炸荷载作用下的钢梁和焊缝区附近埋地X70钢管的动力响应进行数值模拟，研究了不同连接方式对钢框架梁、柱节点抗爆性能的影响和管道焊缝有无余高对管道抵抗变形的影响。甘露等[15]利用ALE(arbitrary Lagrange-Euler)和FSI(fluid-structure-interaction)算法研究不同形式加劲肋加劲板在爆炸荷载下的动力响应和破坏模式，提出增加U形加劲肋端头隔板有利于提高钢板的抗扭性能。

目前，大多数学者对低强度钢结构/构件抗爆性能的研究已经比较广泛，而对高强钢结构/构件抗爆性能研究较少。因此，本文采用显式动力有限元软件ANSYS/LS-DYNA，运用流固耦合计算方法，研究高强钢柱在近爆荷载作用下的动力响应；在此基础上，提出一种简化分段等效三角波计算方法施加爆炸荷载，利用此方法研究影响高强钢柱动力响应的主要因素，为进一步研究高强钢结构/构件抗爆设计提供参考依据。

1 有限元模型的建立与验证

1.1 结构计算模型

如图1所示，高强钢柱采用H型截面，HW350×350×10×16(mm)规格，Q460钢，柱高为4.2 m，钢柱下端固定，上端竖直方向为上下滑动的铰支座，上部钢板厚20 mm，用来施加竖向集中荷载0.5Fp，其中Fp为柱子的稳定承载力。地面混凝土厚度约为200 mm，会反射传播过来的冲击波。炸药采用立方体装药，尺寸为400 mm×400 mm×400 mm，炸药在柱前方2 m处，炸药距离地面的高度为1 m，比例距离为0.42 m/kg1/3，接近于汽车炸药。空气域的6个边界设定无反射边界，防止边界反射波造成的结果失真。

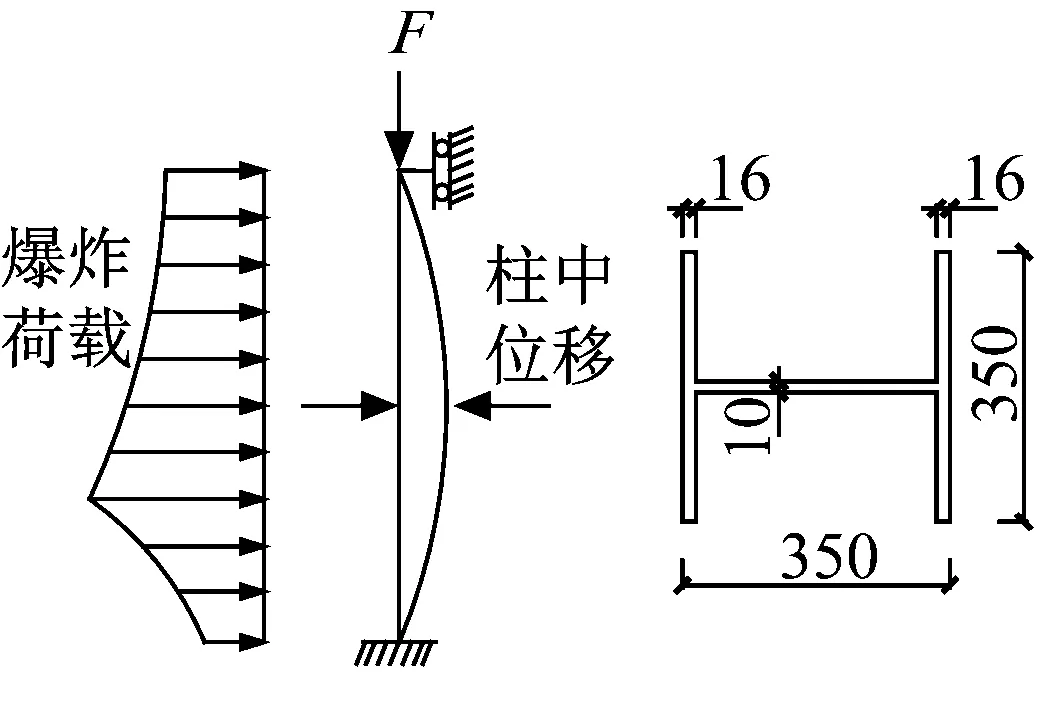
(a) 钢柱模型和作用荷载

1.2 模型的单元类型和材料参数

1.2.1 单元类型

柱子使用显式壳单元SHELL163，网格尺寸为50 mm，文献[16]可以验证该网格尺寸的合理性。混凝土地面、炸药和空气均采用实体单元SOLID164，网格尺寸分别为50 mm、30 mm、70 mm。

1.2.2 炸药材料

对于爆炸的起爆和爆轰等过程采用CJ模型，高能TNT炸药采用的材料模型为MAT_HIGH _EXPLOSIVE_BURN，炸药产物的状态方程为EOS-JWL(equations of state-JWL)，表达形式为

(1)

式中，各符号含义见洪辉的研究。炸药材料参数如表1所示。

表1 TNT炸药材料参数

1.2.3 空气材料

空气材料采用多物质材料模型MAT_NULL，状态方程采用多线性状态方程EOS_LINEAR_POLYNOMIAL

P=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E

(2)

式中：C0～C6为状态方程参数，取C0=-1×105Pa；C1=C2=C3=C6=0，C4=C5=0.4；E为当前内能，取2.5×105J/m3；μ=ρ/ρ0-1，ρ为当前密度，ρ0为初始密度，取1.29 kg/m3；相对体积V0=1.0。

1.2.4 Q460钢材

结构在爆炸冲击荷载下会发生塑性屈服、大变形或断裂等情况，为了准确模拟这种瞬态响应，选用简化的Johnson-Cook模型和LS-DYNA中提供的Plastic-Kinematic塑性随动强化模型。该模型能够很好的模拟各向同性和动态硬化塑性材料，并能通过Cowper-Symonds模型考虑应变率对强度的影响。Q460钢材基本参数如表2所示。

表2 Q460钢材基本参数

1.3 自由空气中爆炸冲击波的数值验证

为验证有限元模型选取是否具有可靠性，建立炸药-空气模型，炸药边长400 mm×400 mm×400 mm，TNT当量104.32 kg，空气域11.6 m×11.6 m×11.6 m，炸药网格30 mm，空气网格70 mm，利用对称性取1/8模型。下面将TNT炸药在自由空气中爆炸的数值模拟结果与3种超压经验公式计算结果以及正压持续时间进行比对。3种超压经验公式如式(3)～式(5)，MPa；正压持续时间经验公式如式(6)，比对结果如图2和表3、表4所示，图2中Ps为超压峰值，Z为比例距离。

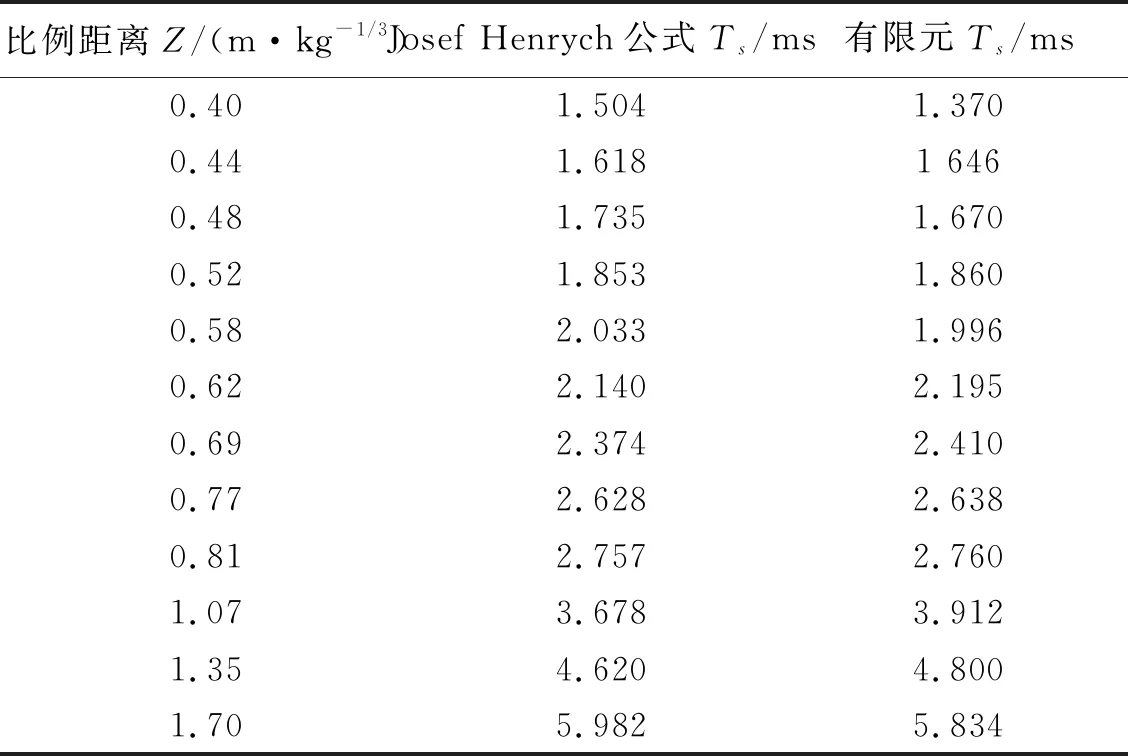
表4 正压持续时间与经验公式比较

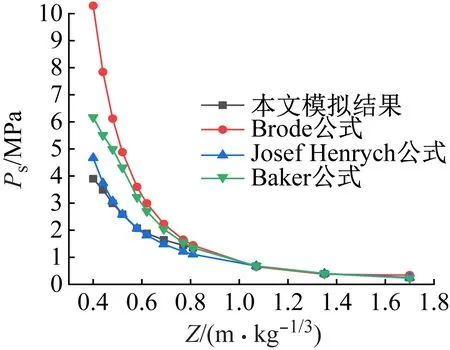
图2 爆炸超压峰值与经验公式的比较

Baker提出空气冲击波超压峰值的经验公式

(3)

Brode提出空气波超压峰值的经验公式

(4)

Josef Henrych用试验的方法得到的经验公式

(5)

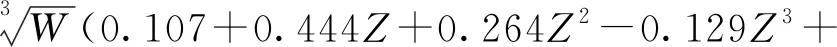
0.033 5Z4)

(6)

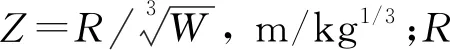
由图2和表3可知：当比例距离大于0.8 m/kg1/3时，不同经验公式计算得到的爆炸冲击波超压偏差逐渐减小，3个公式的曲线基本重合，拟合程度较高。在比例距离较小时，数值模拟结果和Josef Henrych公式最接近，比Brode公式和Baker公式计算结果偏低，4条曲线的走势一致；随着比例距离的不断增大，数值模拟结果与3个公式计算结果的吻合程度不断升高。产生这种现象的原因可能是经验公式是根据球形炸药提出的，而本文采用的是立方体炸药，爆炸初期爆炸冲击波不是以球面形状向外传播，而是以椭球型向外传播，慢慢扩充成球形；此外还与网格尺寸有关。在比例距离为0.4 m/kg1/3时，数值模拟结果和最接近的Josef Henrych公式计算结果相差16.5%，此时误差最大，但在合理范围内。从而验证了有限元模型、材料参数和网格尺寸的合理性及准确性。

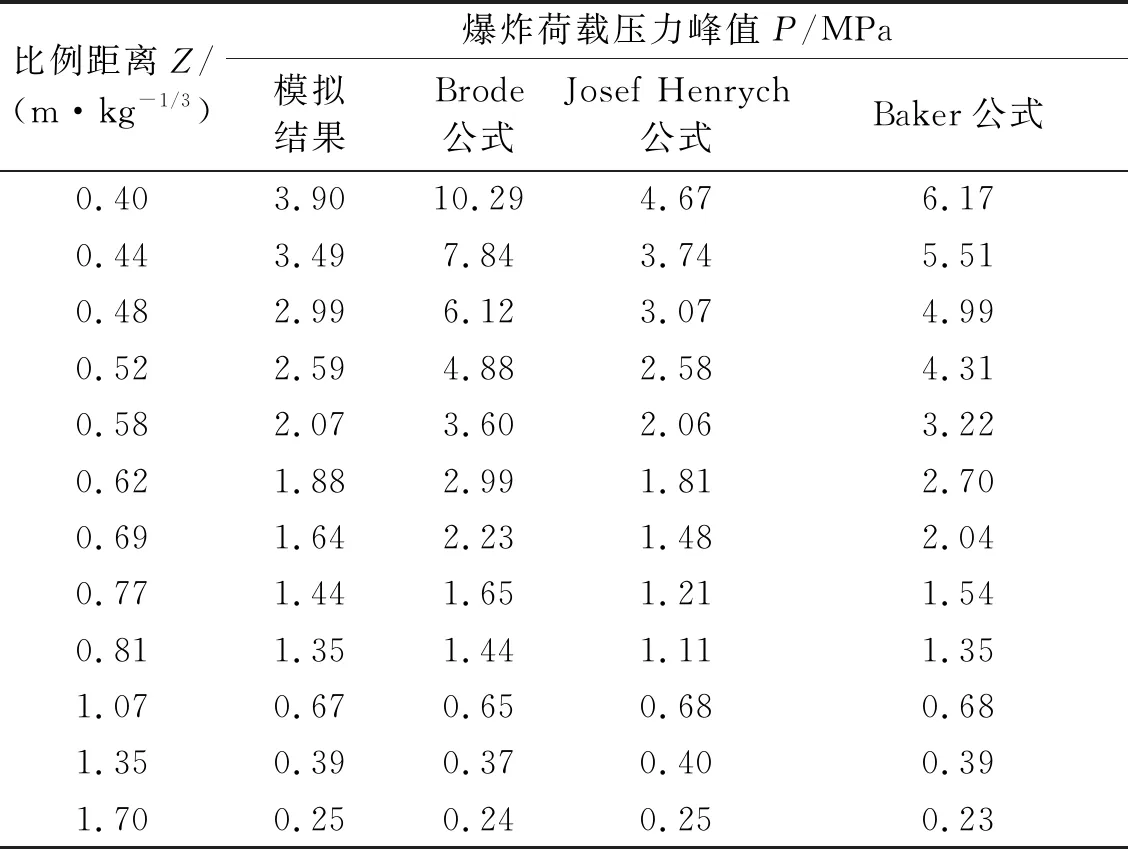
表3 爆炸峰值压力统计表

由表4可知：本文模拟正压持续时间与式(6)计算出的时间比较接近，最大误差为8.9%，在合理范围内，进一步验证了模型的可靠性。

2 冲击波的传播规律与分段等效三角波方法

2.1 冲击波在结构中的传播规律

冲击波是爆炸的瞬间形成的高温且内能巨大的火球不断向外膨胀形成，它压缩周围空气，形成高压气流，以非常快的速度传播，传播速度和压力随着距离的增加而逐渐减小，且衰减速度较快。这时如果建筑结构处在冲击波的传播途径中，建筑结构就会被传来的冲击波包围，从而承受相应的爆炸荷载。建筑物遭到爆炸袭击，不仅直接承受爆炸作用的部位遭到破坏，爆炸冲击波还会通过反射、绕射、以及地面传播，对地面及地下建筑物产生影响。爆炸冲击波的传播和冲击波和结构之间的作用关系如图3所示。

从图3中可知：在t=0.5 ms时，冲击波沿着球状传播，但是在下部遇到混凝土地面时发生了反射，混凝土内力增加；在t=1.5 ms时，爆炸冲击波遇到了柱翼缘下部，在柱表面形成反射波，柱内产生较大应力波；在t=2.5 ms时，应力波呈球状从柱的底部逐渐向上扩散到柱顶；在t=4.0 ms时，冲击波在柱子后部发生波的重组，波从底部向上部逐渐消散。

2.2 等效三角波算法

Baker提出了一种爆炸冲击波随时间呈衰减型的函数曲线

(7)

式中：t为作用时间；α为指数函数衰减率。

在计算过程中常常简化成三角形冲击波压力时程曲线

(8)

(9)

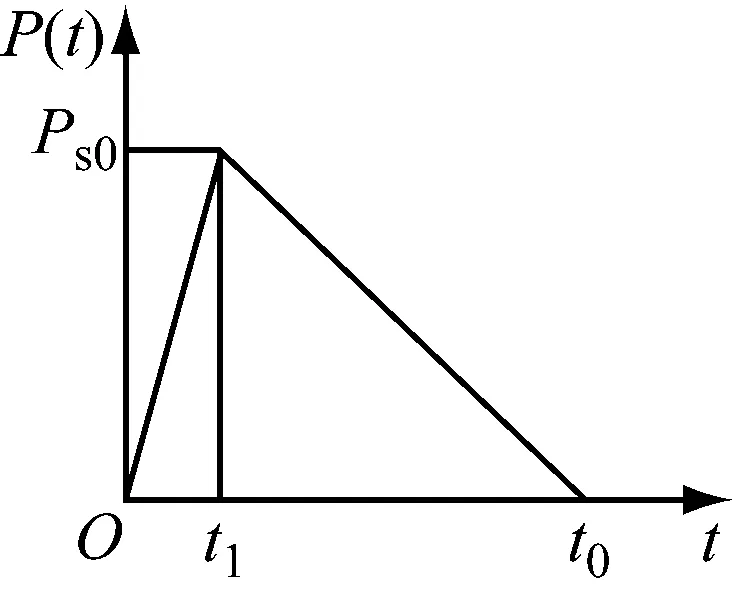
图4 爆炸压力时程曲线图

2.3 沿柱高的分段等效三角波加载

根据爆炸荷载持续时间与结构/构件特征周期T的关系，张秀华给出了当2πtd≤0.4T时为冲量荷载，多为近距离爆炸产生，当2πtd≥0.4T时为准静态荷载，多为远距离爆炸产生，(其中td为爆炸荷载持续时间，T为钢柱的特征周期)。通过有限元分析得到本文所研究钢柱的特征周期最大值为0.079 8 s，最大td为0.003 s，故属于近距离爆炸。通过试验数据和数值模拟结果[18]可知：近爆荷载作用下对结构的破坏程度较大，稳定性降低明显；远爆荷载作用下对结构的破坏较小。

运用流固耦合方法虽然精度高，但是其耗费的成本较大；而施加传统等效三角波的计算方法在计算炸药近距离爆炸时误差较大；为进一步简化计算方法和节约计算成本，提出了一种分段等效三角波加载方式。

“分段等效三角波加载”方式不需要建立空气域、炸药和地面，只需要建立计算的结构模型。先将要计算的工况按流固耦合的方法计算后，将柱前和柱后分别分成m个区域，每一个区域选取一个居中的荷载超压峰值和荷载冲量，提取出m个不同时间-荷载函数之后分段分别施加给结构进行计算，计算时间大约只需要3～15 min，极大的缩短了计算时间，而且误差在合理的范围内。加载示意图如图5所示。

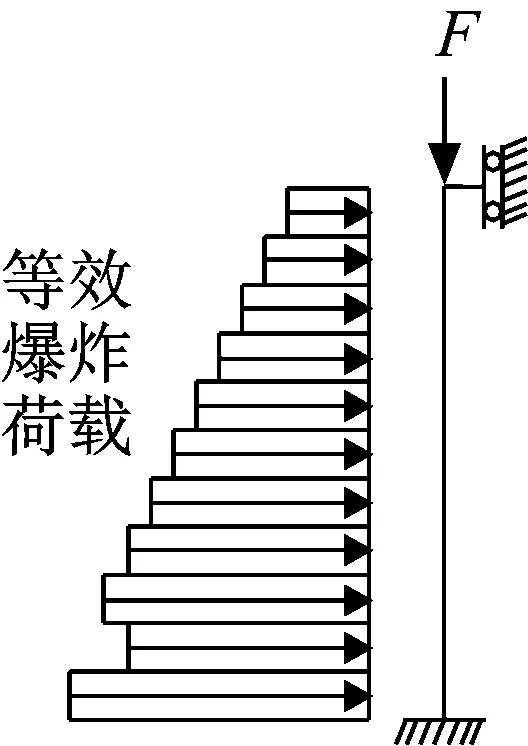
图5 分段等效三角波加载示意图

如图6，先用流固耦合的方法计算出同一比例距离情况下的钢柱前和柱后表面的超压峰值和荷载冲量，将4.2 m高的柱子分成11个区域(区域分的越多，最后的计算结果越精确)，选取一个居中的超压峰值和荷载冲量，把他们以时间为函数写入命令流中，提取出11个不同时间-荷载函数之后分段分别施加给结构，并最终得到计算结果。

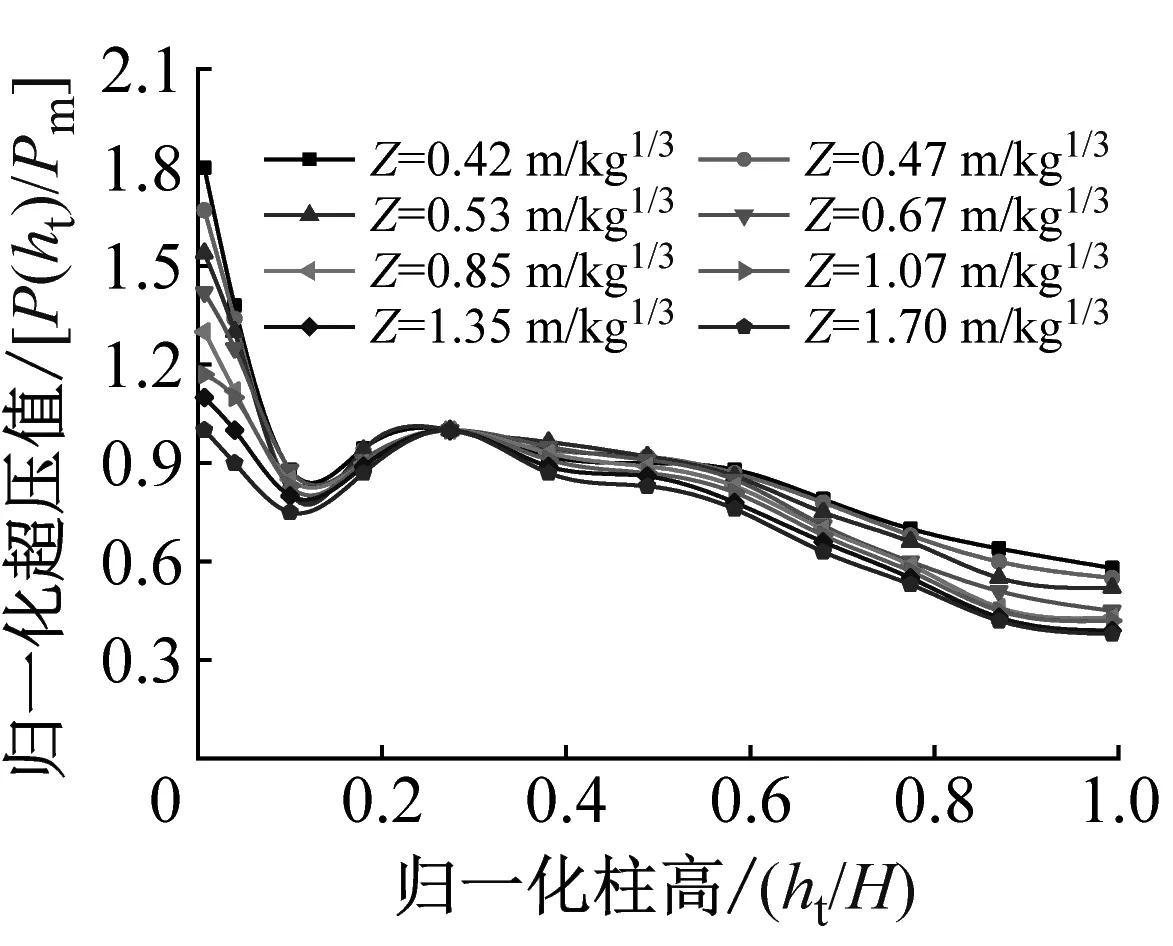
(a) 冲击波峰值沿柱高分布

图6给出了爆炸冲击波大小、冲击波峰值到达时间和冲量的大小沿柱高的分布情况，其中压力峰值、冲量和柱高都做了归一化的处理，分布柱高做整体柱高4.2 m的分子，而冲击波的归一化的分母为与炸药高度相同处的柱表面荷载峰值。图6中：ht为炸药位置距柱底高度；Pm为和炸药等高处的柱表面的超压峰值；P(ht) 为沿柱高度处的超压峰值；Im为和炸药等高处的柱表面的冲量峰值；I(ht)为沿柱高度处的冲量峰值；t′为爆炸冲击波峰值到达时间。可以看出，当比例距离Z<1 m/kg1/3时，爆炸荷载的地面反射及聚流在柱底1/10以内比较明显，而且贴近地面时的冲击波增大幅值较大。但是在比例距离Z>1 m/kg1/3时，地面反射变的不明显。而在其他部位，冲击波的大小都随着与炸药同高柱前部位的远离而变小，尤其是在柱脚到炸药高度(0.1～0.2倍柱高)这一段，冲击波大小下降明显，这可能是由于地面反射波和爆炸冲击波有反方向抵消的原因。

图7为运用分段等效三角波加载方式和流固耦合方式计算同一工况结构变形的结果。图7中：Δ为位移；t为时间。

图7 两种计算方法下柱中位移

由图7所见，两种方法的计算结果曲线走势一致，数值比较接近，验证了分段等效三角波方法的可行性。用流固耦合方法计算一个工况通常需要5～48 h，而做爆炸分析需要模拟大量的工况，这就需要耗费大量的人力物力，分段等效三角波加载方法计算简便，大大缩短了计算时间，节约了计算成本，可以广泛的应用在建筑结构的爆炸分析中。

3 钢柱的动力响应和破坏模式

3.1 动力响应分析

选用6 m柱高，柱截面仍为HW350×350×10×16 (mm)，Q460钢材，炸药尺寸400 mm×400 mm×200 mm，TNT当量52.16 kg，比例距离为0.53 m/kg1/3，轴压比为0.2。图8为钢柱在不同时刻的钢柱整体变形情况，图8中：h为柱高；图9为钢柱各测点位移时程曲线。

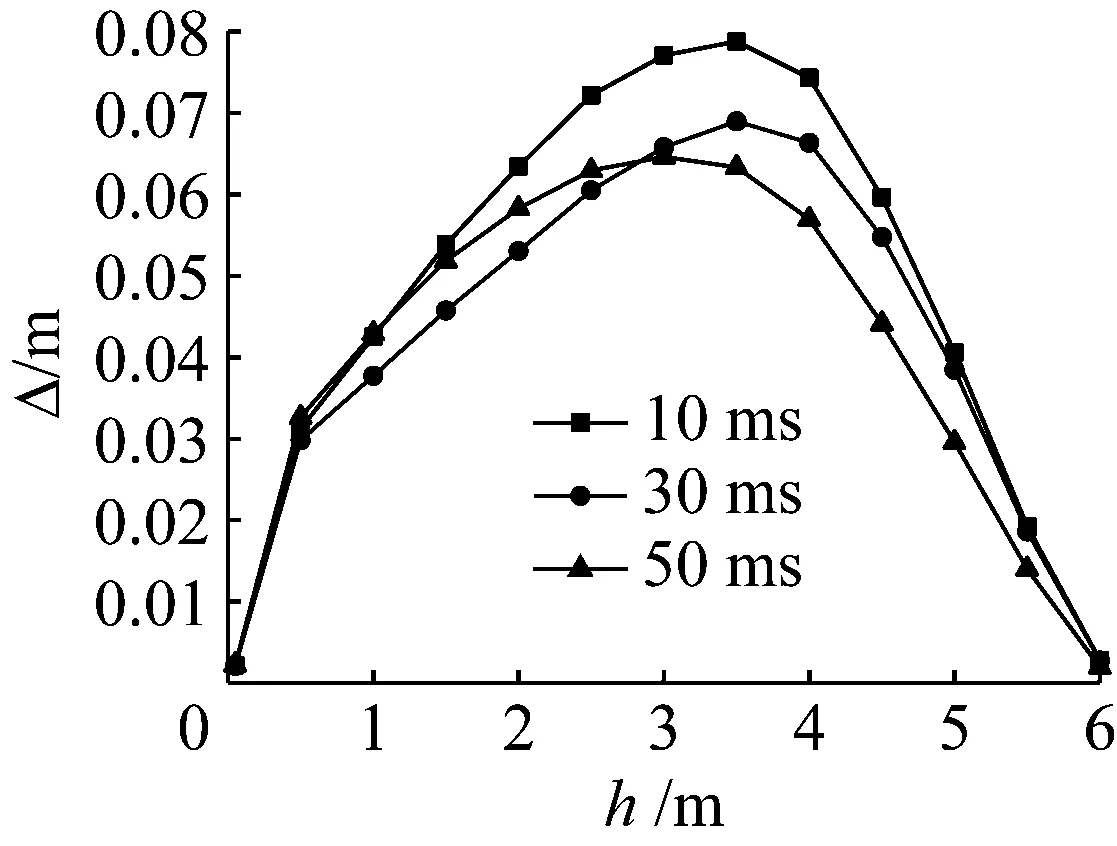
图8 不同时刻钢柱整体位移时程曲线

由图8可知，在爆炸发生10 ms时，柱脚处塑性变形呈线性增长，柱中位移达到77 mm，此时最大位移发生在钢柱高度3.5 m处，达到了80 mm。当爆炸时间到达30 ms时，柱脚处的塑性变形没有变化，柱中位移和最大位移均有所下降，此时最大位移为68 mm，较爆炸10 ms时下降了15%。爆炸荷载结束时，柱脚处位移跟之前的基本重合，柱脚处的塑性位移在30 mm左右，而柱中位移趋于平缓，最大位移高度也下降到了柱中位置处，此时最大位移为64 mm，和爆炸10 ms相比下降了20%，原因是钢柱响应由一开始的弹性变形逐渐恢复至塑性变形。

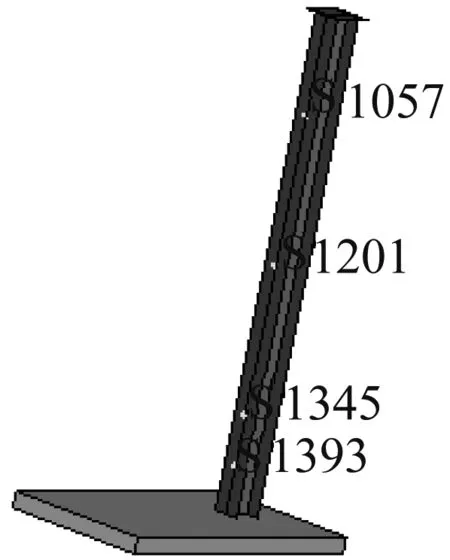
如图9所见，在距柱底0.1 h、0.2 h、0.5 h和0.8 h的翼缘与腹板相交处分别布置了一个测点。从各测点的位移时程曲线可以看出，位于柱中间位置的1201号测点在9.4 ms和30 ms发生位移峰值最大，位移峰值在20～80 mm区间呈来回震荡的衰减趋势。1057号测点与1201号测点曲线趋势基本一致，这两个测点位置仍处于弹性状态，没有发生破坏。与炸药爆心等高处的1345号测点与离柱脚位置最近的1393号测点曲线走势一致，位移在小幅度来回震荡，此时这两点已经进入到塑性阶段。

(a)

3.2 H型钢柱的破坏模式

钢柱的破坏模式主要有3种：柱中弯曲破坏，柱脚附近剪切破坏和弯曲剪切联合破坏，如图10所示。

(a) 柱中弯曲破坏

钢柱发生的破坏模式与轴压比、比例距离以及两端约束方式等有关。本文模拟的钢柱破坏形式在轴压比小于0.5时发生剪切破坏，轴压比大于0.5时以弯剪联合破坏为主，产生弯剪联合破坏模式的原因是当比例距离很小时，爆炸荷载作用下产生的冲击波传播迅速，柱子截面应力快速增大到破坏应力，此时弯曲应力并没有得到充分发展；另外钢材的强度等级较高，冲击波经过地面反射使得柱子底部承受的应力较大，导致柱脚处比其他位置更容易破坏。

4 影响高强钢柱动力响应的因素

为探究Q460钢柱在不同参数下的动力响应，研究了约束方式联合轴压比、钢材强度、柱子迎爆面位置等因素对钢柱在爆炸荷载作用下动力性能的影响。

4.1 约束方式联合轴压比的影响

选用6 m的柱高，柱截面尺寸不变，Q460级钢材，炸药TNT当量53 kg，比例距离为0.53 m/kg1/3。工况分别选取了不同的轴压比和不同的约束方式。轴压比分别为0、0.2、0.5、0.7和0.9，5种约束方式，如图11所示。

图11 钢柱的不同约束方式

图12给出了Q460钢柱在不同约束下不同轴压比的柱中位移曲线。从图12(a)～图12(c)中可以看出在柱两端固结程度比较高的情况下钢柱的破坏程度相对较低，3种轴压比下柱中位移曲线趋势一致，也就是由爆炸冲击波引起的初始弹性变形基本一致，破坏程度极为接近，说明在钢柱两端约束程度相对较高时，轴压比对钢柱的破坏影响并不显著。而在钢柱上部约束较少的图12(d)、图12(e)图中发现，柱子位移较大，普遍破坏严重，且还呈不断发展的趋势，尤其是轴压比为0.7的钢柱破坏最严重，这表明钢柱的约束程度越低，轴压比的影响越明显。图12中μ表示轴压比。

(a) t=0.5 ms

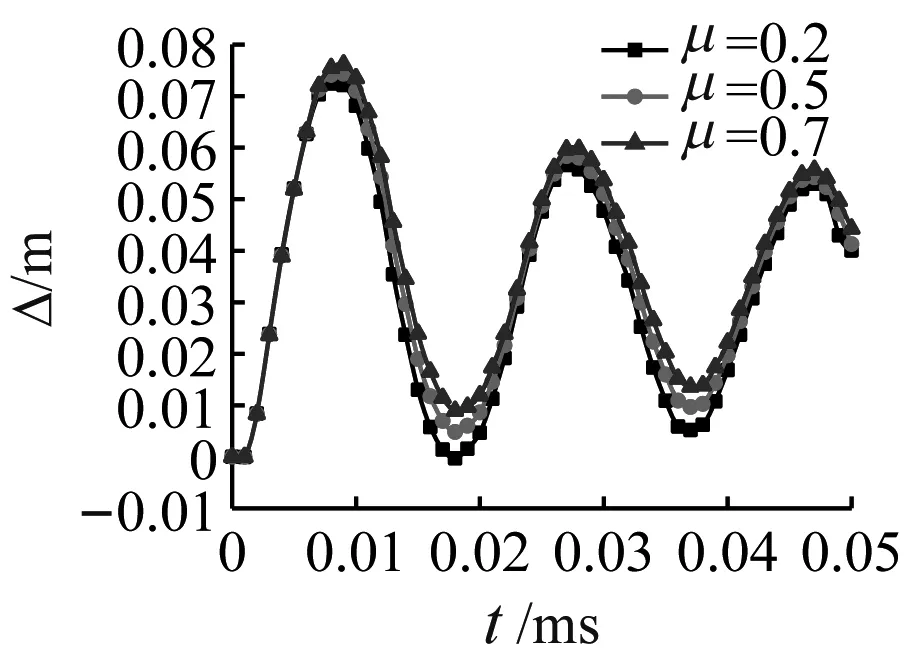
(a) 下固上固定铰

4.2 钢柱强度等级的影响

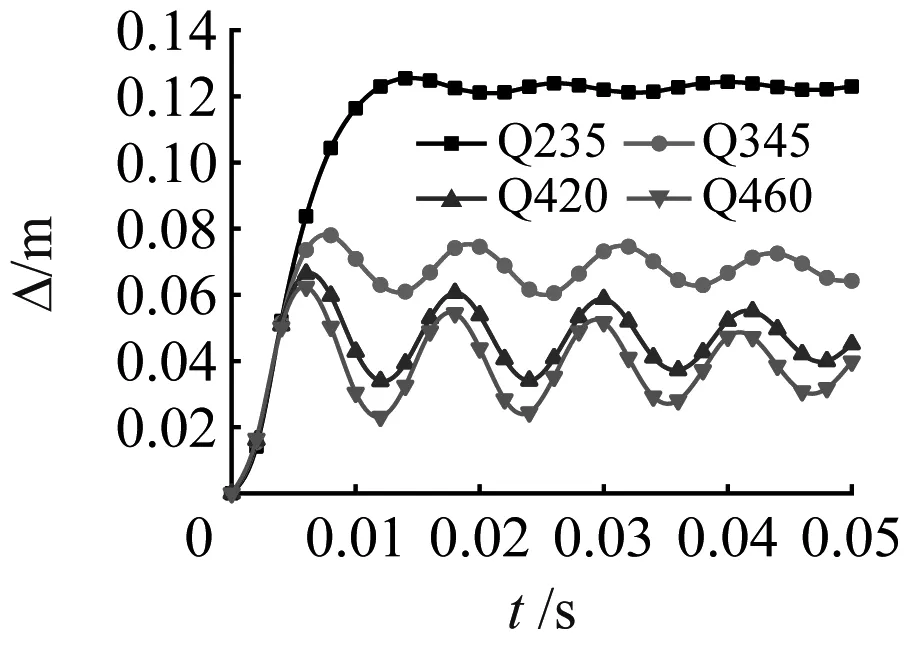
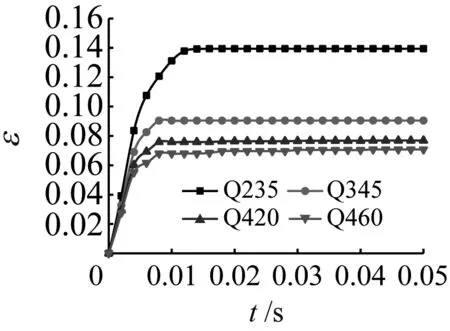
钢材的强度等级会在爆炸冲击荷载作用的过程中对钢柱的破坏产生一定的影响。为了定性和定量分析这种影响，对柱子高度分别为4.2 m和6.0 m，钢材强度分别为Q235、Q345、Q420和Q460的钢柱的柱中位移和塑性应变进行分析。位移时程曲线和塑性应变时程曲线如图13～图14所示。

(a) h=4.2 m

由图13可见：当柱高度为4.2 m时，Q235强度的钢柱柱中位移最大，最大位移值达到了125 mm，柱中位移随着钢柱强度等级的提高逐渐变小，Q345、Q420、Q460级钢的柱中最大位移分别减小到80 mm、63 mm和60 mm。当柱高为6 m时，强度为Q235的钢柱首先发生破坏，Q345、Q420、Q460级钢柱的柱中位移在一个平衡位置振荡，没有发生破坏，可见提高钢柱强度等级能有效防止柱子变形过大。

图14给出了不同强度等级的钢柱的柱脚处等效塑性应变，一般认为材料超过给定的失效应变时则判定为破坏。此处普通钢(Q235和Q345)的过大应变取5%。由于高强钢的塑性有降低趋势，所以此处高强钢(Q420和Q460)的过大应变取4%。从图14中可以明显看出柱高在4.2 m和6.0 m时Q235钢的等效塑性应变最高都达到14%以上，接近失效应变，破坏程度较高，而钢柱柱脚处的等效塑性应变随着钢材强度等级的提高大幅降低。说明随着钢材强度的提高，塑性降低不明显，因此高强钢可以更好的抵抗爆炸冲击作用。图14中，ε为塑性应变。

4.3 炸药距地面高度的影响

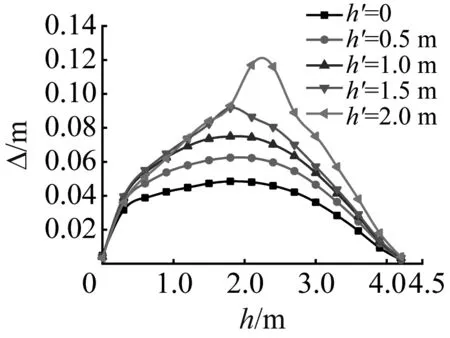
炸药在不同高度起爆会对建筑物产生不同程度的破坏，图15给出了炸药在不同高度情况下钢柱整体的变形情况。图15中,h′为炸药高度。

(a) 位移峰值

从图15可以看出，钢柱的位移峰值曲线和塑性位移曲线呈现相同的趋势。在柱高为0.25 m以内时，虽然炸药高度不同，但是位移峰值曲线和塑性位移曲线都基本重合。从图15(a)可以看出，随着炸药位置的不断升高，位移峰值也不断增大，最大位移峰值基本都发生在柱中位置。从图15(b)中可以看出，当炸药处于地面上和炸药高度0.5 m时，最大塑性位移并不发生在柱中位置，而是发生在柱子下端1/4处。由此可见，起爆位置较低时，柱脚容易发生剪切破坏，起爆位置越高，柱中位移越大，越容易发生弯曲破坏。

4.4 柱子迎爆面位置的影响

钢柱迎爆面位置不同，其产生影响也不同。本节采用近距离汽车炸药，TNT炸药在距离地面1 m高处，炸药距离钢柱的水平距离为2 m处，炸药TNT当量53 kg，比例距离为0.53 m/kg1/3。迎爆面位置不同时的钢柱破坏情况，如图16所示。

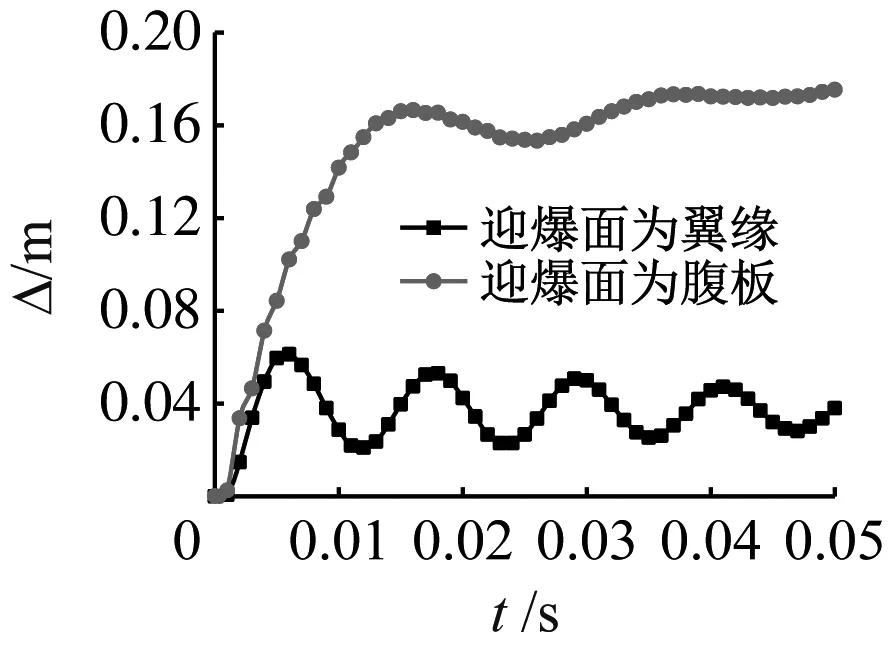
(a) h=4.2 m

由图16见，在柱高为4.2 m时，腹板为迎爆面时的柱中位移要比翼缘为迎爆面时大很多，后者的位移平衡位置在40 mm左右，而前者的位移达到170 mm，并且还有继续发展的趋势，说明此时钢柱的破坏非常严重。当柱高为6 m时，翼缘为迎爆面时的柱中位移的平衡位置大约在50 mm左右，而腹板作为迎爆面时的钢柱柱中位移急剧增加，钢柱最终发生弯剪破坏而倒塌。这些都说明翼缘作为迎爆面时钢柱更能抵抗爆炸荷载的作用。这是由于当腹板作为迎爆面时，产生的弯矩绕弱轴刚度较小，而且爆炸冲击波到达腹板位置时会在翼缘和腹板之间的半封闭空间内时会形成冲击波的涡流，从而使得翼缘和腹板连接处的受力较大。

4.5 截面宽厚比的影响

本节选取了3种截面形式的钢柱，截面尺寸分别为HW330×350×10×16(mm)、HM330×350×14×16(mm)、HN330×350×10×18(mm)，柱高均为4.2 m，炸药TNT当量53 kg，比例距离均为0.53 m/kg1/3，对应表5中模型1～模型3。

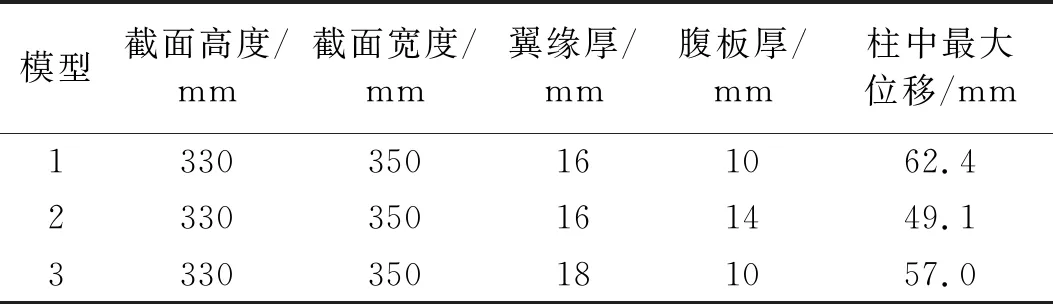
表5 各种宽厚比的破坏程度

从表5中可以看出：比较模型1和模型2，在截面高度、截面宽度、翼缘厚度相同时，腹板厚度较大的模型2柱中最大位移小了13.3 mm，即腹板宽厚比越小，对钢柱的抗爆越有利；比较模型1和模型3，截面高度、截面宽度和腹板厚度相同时，翼缘厚度较大的模型3柱中最大位移减小了5.4 mm，即翼缘宽厚比越小，在爆炸荷载作用下钢柱破坏程度越轻。由此可知，减小翼缘和腹板的宽厚比可以减小钢柱在爆炸荷载作用下的破坏程度，其中减小腹板的宽厚比效果更明显。