半正弦循环交通动载下加筋砾性土动力特性研究
2022-02-22王家全侯森磊林志南黄世斌
王家全, 侯森磊, 林志南, 黄世斌
(1. 广西科技大学 土木建筑工程学院, 广西 柳州 545006;2. 广西壮族自治区岩土灾变与生态治理工程研究中心, 广西 柳州 545006)
砾性土是指砾粒含量从0%~80%的含有多粒组成分的宽级配粗粒土,是包含砾砂、粉砾土、砾类土等在内的天然土壤,因其具有良好的力学性能和透水性能而被作为路基填料广泛应用于路基工程中[1]。然而砾性土等颗粒状材料具有级配范围较大,且多具有不均匀、不连续的不良工程特点,而在土中加筋有增大土体模量,提高土体的抗拉抗剪强度,提升土体工程性能,增加土体结构稳定性的优点,因而土体加筋技术已被广泛应用于路基工程中[2-4]。
目前,在加筋土动力特性方面已有部分学者开展了相关研究。高超[5]通过对土工格栅加筋碎石土的动三轴试验发现动应力和动应变的关系呈现硬化型,动应力越大,动应变越大,并指出围压是影响加筋土强度的最大因素。Latha等[6]对加筋砂土进行了大型动三轴试验,结果表明低围压下动模量不会随加筋层数的增加而改变,但在高围压下随着加筋层数的增加动模量显著增大。Moayed等[7]进行了在不同循环应力比下土工织物加筋砂土的循环三轴试验,发现加筋层的布置能明显降低试样变形,提高试样剪切模量。刘飞禹等[8]通过单调直剪试验和循环直剪试验,研究了筋土界面的动力特性,发现循环剪切会降低筋土界面的抗剪强度。Zheng等[9]通过振动台模型试验研究了加筋土桥台挡墙的动力特性,发现筋材竖向间距和筋材抗拉强度对挡墙墙面侧向位移及桥台沉降的影响最大。Liu等[10]则通过大量的动力有限元分析研究了加筋土挡墙的地震响应,并指出在分析强地震作用下的加筋土结构时应充分考虑波浪传播和结构动力学的基本原理以及回填土的弹塑性变形。
然而,上述学者的研究对象都是平铺加筋土,对于其他新型加筋土研究对象,国内外研究成果则相对较少。李丽华等[11]通过加筋土挡墙模型试验发现使用废旧轮胎代替土工格栅也能有效减小墙面侧向位移和墙顶竖向位移。张孟喜等[12-13]在竖向加筋的基础上结合传统平铺加筋,首次提出了H-V(水平-竖向)立体加筋的概念,并采用镀锌铁皮、橡胶板和有机玻璃等材料作为筋材进行了立体加筋砂土三轴试验,肯定了立体加筋工程性能的优越性。邱成春等[14-15]通过以有机玻璃为加筋材料的水平-竖向立体加筋饱和砂土的动三轴试验,并利用PFC2D离散元软件进行了数值模拟分析,研究了水平-竖向加筋饱和砂的动力特性随围压、动应变、竖筋高度变化的规律。
阻尼比也是土体动力特性的重要参数之一,其选取将直接影响着工程质量。因此,对阻尼比的研究具有重要的工程意义[16]。目前,学者们多采用等效阻尼的计算方法,即以滞回圈的面积与滞回圈顶点至原点的连线与横轴形成直角三角形面积的比值乘1/(4π)的系数得到阻尼比[17]。刘飞禹等[18-19]等则将阻尼比的计算方法应用于土工合成材料与土体界面的动剪特性分析中。一般对土体阻尼比的研究中,施加的动载多为正弦波,黄博等[20]通过动三轴试验模拟高速列车荷载,发现不使土体产生负应力应变的半正弦波与实际列车荷载较为吻合。魏新江等[21]采用等效阻尼的计算方法研究了地铁半正弦循环荷载下冻融土的阻尼特性,提出了冻融土阻尼比与累积轴向应变之间的函数关系。而赵莹莹[22]则基于曼辛准,通过研究正弦波与半正弦波循环荷载下试样滞回圈面积比得到半正弦循环荷载下试样的阻尼比计算公式。但以上学者均未进行半正弦循环荷载下土体阻尼比计算公式的详细推导说明。
且在新型立体加筋方式的研究中,学者们多选用镀锌铁皮、橡胶板、有机玻璃等作为筋材,较少采用工程现场常用的土工格栅作为加筋材料进行试验,且也很少以路基路面填料砾性土作为试验土体。基于此,以工程常用土工格栅为加筋材料,以无筋、平铺、环形竖向、环形立体组合加筋等不同加筋形式的砾性土为对象开展半正弦循环荷载下的动三轴力学试验,研究交通荷载下不同加筋工况下加筋砾性土的应力应变特性,验证新型立体加筋结构性能的优越性。同时进行半正弦循环荷载下土体阻尼比计算公式的推导。并在此基础上进行不同加筋层数及围压下的环形立体组合加筋砾性土动三轴试验,进一步研究环形立体组合加筋土的动力特性。
1 试验概况
1.1 试验材料
试验所用土样为广西柳州地区路基工程常用的河砂,经筛分试验,剔除粒径为0.5 mm以下颗粒后,得到该土样的粒径范围为0.5~10.0 mm,不均匀系数Cu=5.0,曲率系数Cc=1.25,可知该土样为级配良好的砾砂,该土样的级配曲线如图1所示。该砾砂土粒比重为2.67,其最大干密度为1.81 g/cm3,最小干密度为1.56 g/cm3,自然干密度为1.71 g/cm3。考虑试验的可操作性,选取网孔尺寸20 mm×20 mm的小网孔双向 塑料土工格栅作为加筋筋材,该双向土工格栅纵肋宽度为3 mm,横肋宽度为2 mm,纵向抗拉强度为18.6 kN/m,横向抗拉强度为15.4 kN/m。
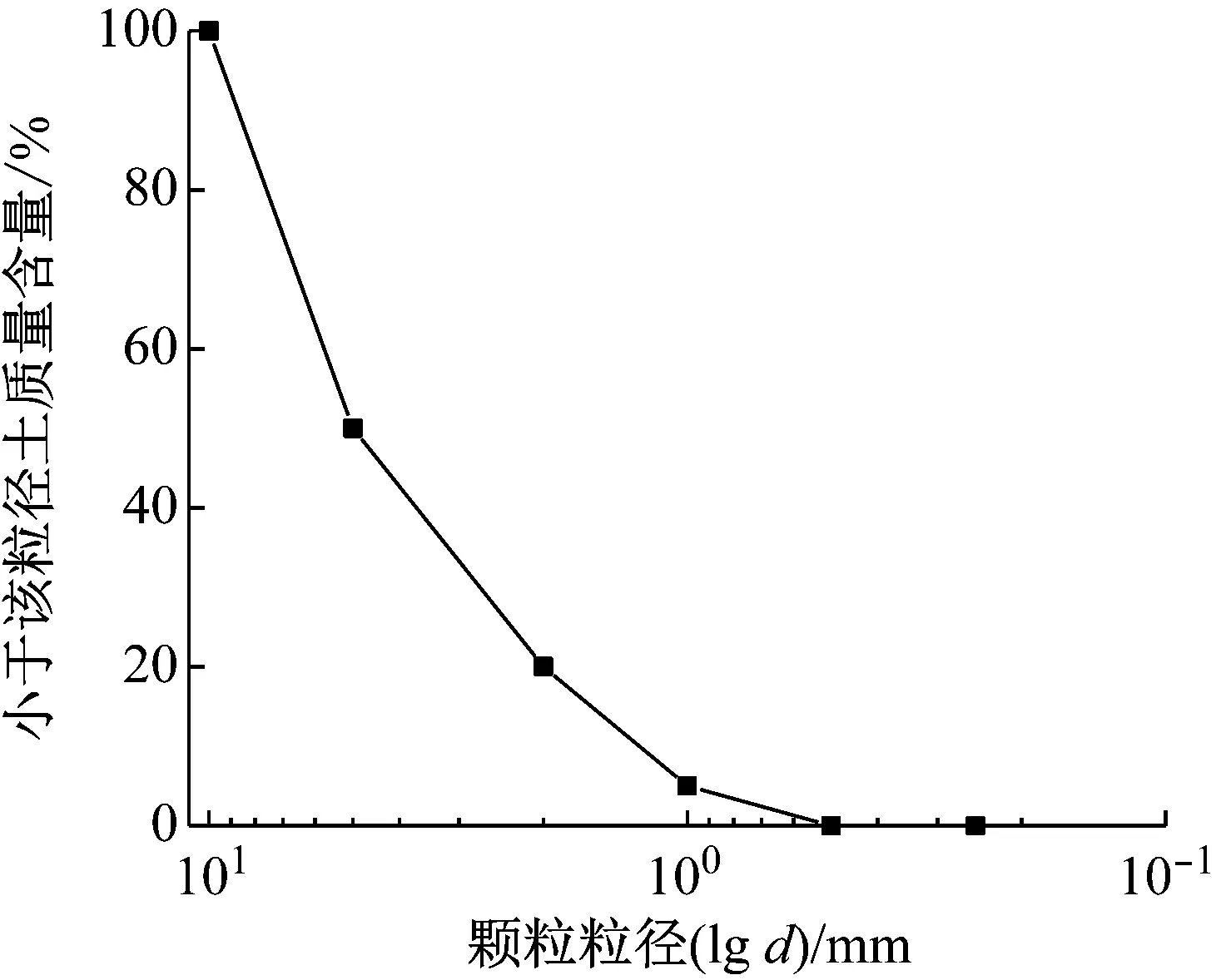
图1 砾砂级配曲线
1.2 试验仪器
试验所用仪器为GDS动态三轴测试系统。该系统所能施加的最大轴向力为10 kN,最大围压和反压均为2 MPa,可施加的频率范围为0~5 Hz。试验过程中的轴向动应力、动应变、动孔隙水压力、试样体变量等均可通过系统配套的传感器和数据采集及控制程序来实现数据的实时监测与采集。本次试验中设置每个循环采集20个数据,即频率为1 Hz时为每0.05 s采集一次数据。
1.3 试验方案
为了研究交通荷载下,不同加筋形式对砾性土路基的长期动力特性的影响规律,以无筋、平铺、环形竖向与环形立体组合加筋土为研究对象,开展固结不排水动三轴试验。同时为了研究环形立体组合加筋土的动力特性,设计了不同加筋层数的环形立体组合加筋土在不同围压下的固结不排水动三轴试验,试样为直径100 mm高200 mm的圆柱形试样,具体工况如表1所示,各加筋形式示意图如图2所示,筋材布置位置图如图3所示(平铺筋材为对角线长度为100 mm的正方形格栅;通过用细钢丝在格栅横肋处进行绑扎,制成环形筋材,环形筋材高度h为25 mm,环形筋材直径为70 mm;环形立体组合加筋方式中平铺筋材和环形筋材没有进行连接)。

(a) 平铺加筋
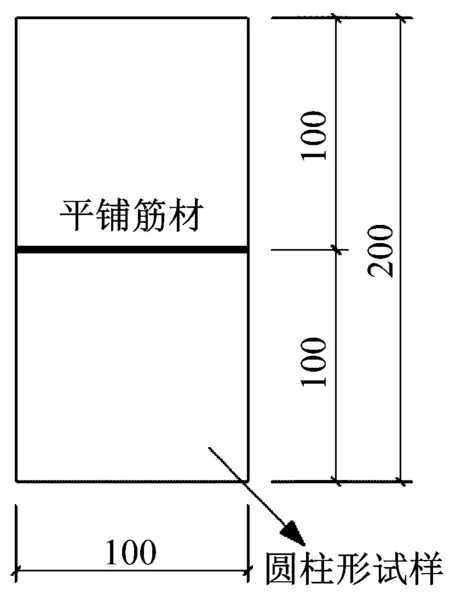
(a) 平铺加筋
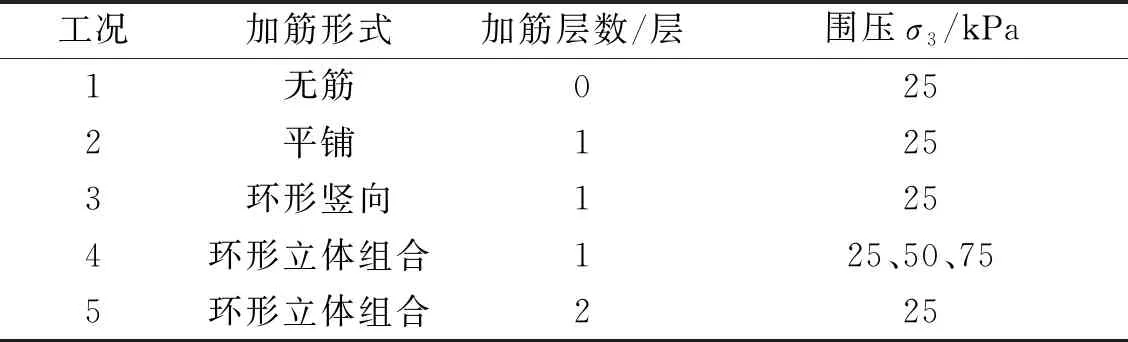
表1 试验工况列表
试验的循环荷载波形为半正弦波,如图4所示,循环荷载频率为1 Hz。试验围压则是依据铁道路基中土体自质量应力和轨道自质量之和来选取,同时为方便试验操作及数据处理,取围压25 kPa作为浅层路基围压。同时考虑围压对加筋砾性土力学性能的影响,故本试验中围压选用25 kPa、50 kPa、75 kPa。参考TB 1001—2016《铁路路基设计规范》中的列车荷载数值,将第一级循环荷载动应力幅值取为50 kPa。根据铁路路基设计规范中列车动荷载计算公式

图4 多级半正弦波加载波形
σd,max=0.4Ps(1+αv)/(l×b)
(1)
式中:σd为路基顶面动应力幅值;Ps为列车静轴重;α为动力冲击系数,普通线路取0.005;v为列车速度;l为枕轨长度;b为枕轨宽度。取列车轴重20 t,即Ps=200 kN,v=90 km/h,l=3.0 m,b=0.25 m,算得动应力幅值σd=154 kPa。为方便试验数据的处理,将动应力幅值取为150 kPa。基于此,本次试验的加载方式设计为初始动应力幅值σd=50 kPa,等差为100 kPa的多级加载方式,即施加的动偏差应力为0~50 kPa、0~150 kPa、0~250 kPa、0~350 kPa……参考马少坤等[23]的多级动三轴试验,将每级循环荷载振次定为3 000次,直至试验达到破坏标准,即GB/T 50123—2019《土工试验方法标准》规定的轴向应变达到5%时终止试验。
试样采用烘干后的砾性土进行制样。每组试样质量2 800 g,分5层击实装样,控制每层砾性土质量为560 g,每层击实次数为30次,从而使每组试样的密实程度保持一致,即相对密度为0.89。制样完毕,待压力室通满水后,进行CO2饱和和水头饱和,当孔隙水压力系数B≥0.95时,则试样饱和完毕。试样饱和后进行固结比为1的等向固结,当反压体积不再变化时,则认为试样已经固结完毕。然后再施加循环荷载。
2 试验结果分析
2.1 阻尼比分析
阻尼比λ与能量损失数Ψ之间的关系为
(2)
式中:ΔW为一个加载周期内损耗的能量;W为动载作用的总能量。在动载下,土体动应力可表示为动弹性应力与动黏性应力之和,如式(3)所示
(3)
半正弦循环荷载的加载函数如式(4)所示
(4)
故
(5)
式中:σd为动应力;εd为动应变;E为弹性模量;c为阻尼系数;σm为动应力幅值。
解微分方程式(5),得
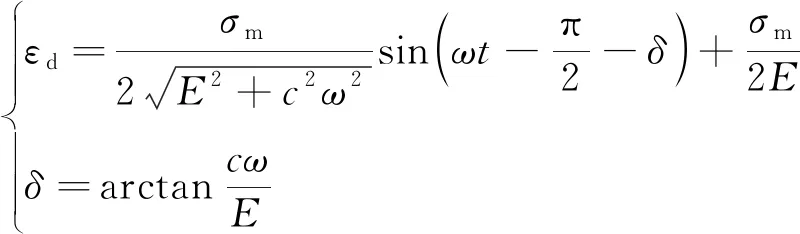
(6)
式中,δ为应变与应力间的相位差。
为计算方便,令
(7)
由于E远大于cω,故为后续计算方便,将式(6)第二项的分母E改写成Ed,如式(8)所示
(8)
则Ed为动弹性模量,动应变幅值εm的可由动应力幅值除于动弹性模量得到,如式(9)表示
(9)
故半正弦循环荷载下土体动应变函数可由式(10)表示
(10)
此时,半正弦波荷载下的土体滞回圈如图5(a)所示,将动应力和动应变进行归一化处理
(11)
(12)
令
(13)
(14)
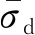
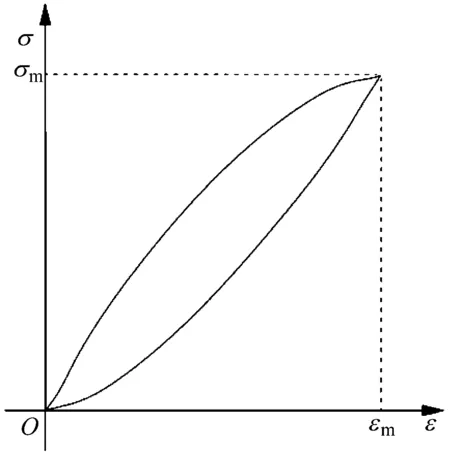
(a) 半正弦循环荷载下的原始滞回圈
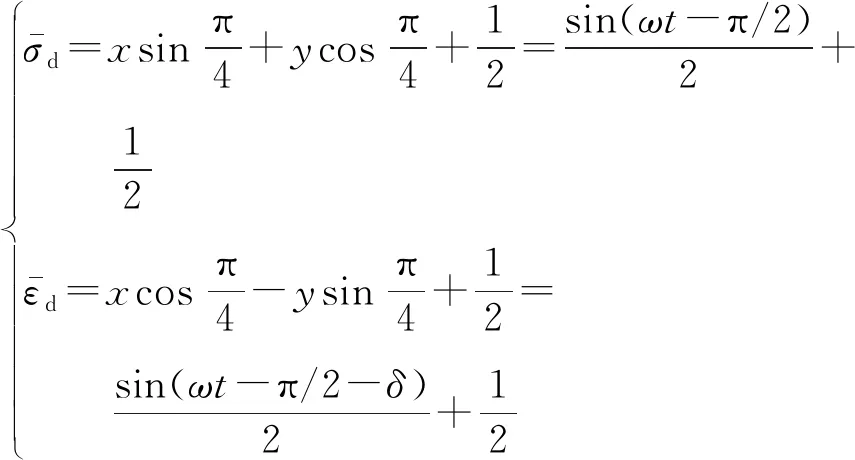
(15)
整理,得
(16)
由式(16)可知,转换坐标后,滞回圈为标准椭圆,故滞回圈的面积S为式(17)所示
(17)
土体在一个周期内损耗的能量等于阻尼力所做的功,则损耗能ΔW的计算如式(18)所示
(18)
动载在一个周期内对土体作用的总能量W如式(19)所示
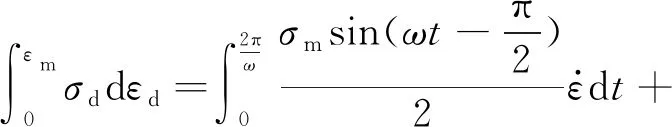
(19)
将式(18)、式(19)代入式(2),故半正弦循环荷载下土体阻尼比的计算公式如式(20)所示
(20)
式中:S为滞回圈面积;SΔ为滞回圈顶点至原点连线与横轴形成直角三角形面积。将式(20)分母中滞回圈面积项去除,即得到正弦波循环荷载下土体阻尼比的计算公式,如式(21)所示
(21)
2.1.1 加筋形式
各级循环荷载施加初期试样处于不稳定阶段,不具有代表性,对数据分析后发现,在第10个循环时已经趋于稳定,这与Kokusho[24]试验研究结果相一致,故取每级循环荷载的第10个循环运用式(20)计算出的阻尼比作为本级荷载下试样的阻尼比。围压25 kPa下不同加筋形式下环形立体组合加筋试样的阻尼比-动应力曲线,如图6所示。由图6可知,多级循环荷载下加筋试样的阻尼比呈现前期增大随后减小的规律,阻尼比在动应变达到1%左右达到峰值。这是由于前期荷载施加,土体受到循环荷载的振密作用,试样内部颗粒互相移动,消耗的能量增大,阻尼比增大。当试样达到密实状态,刚度增大,消耗的能量也减小,故阻尼比也减小。从图7还可看出,加筋试样的阻尼比均小于无筋试样,这与邱成春等的试验结果相一致。且加筋试样阻尼比随着加筋形式的变化而变化,无筋砾性土试样的最大阻尼比为0.016,平铺和环形竖向加筋砾性土的最大阻尼比分别为0.015 51、0.014 99,环形立体组合加筋试样的最大阻尼比最小,为0.014 82,这是由于加筋增大了砾性土试样的刚度导致其阻尼比减小,且环形立体组合加筋对砾性土试样的刚度提升效果最好。
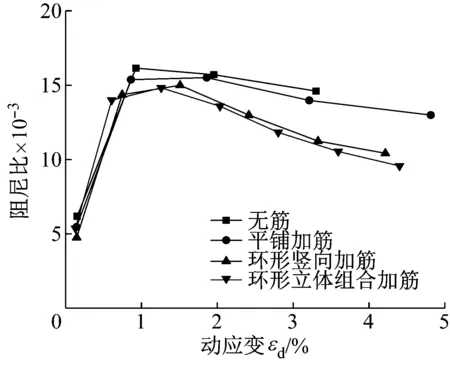
图6 不同加筋形式试样阻尼比-动应变曲线
2.1.2 加筋层数
围压25 kPa下不同加筋层数下环形立体组合加筋试样的阻尼比-动应变曲线,如图7所示。由图7可知,与无筋试样阻尼比相比,1层环形立体组合加筋试样的最大阻尼比减少了8.2%,2层环形立体组合加筋试样阻尼比减少了10.7%,仅比前者减少了2.5%,即随着加筋层数的增加,环形立体组合加筋对砾性土试样最大阻尼比的削弱效果减弱。
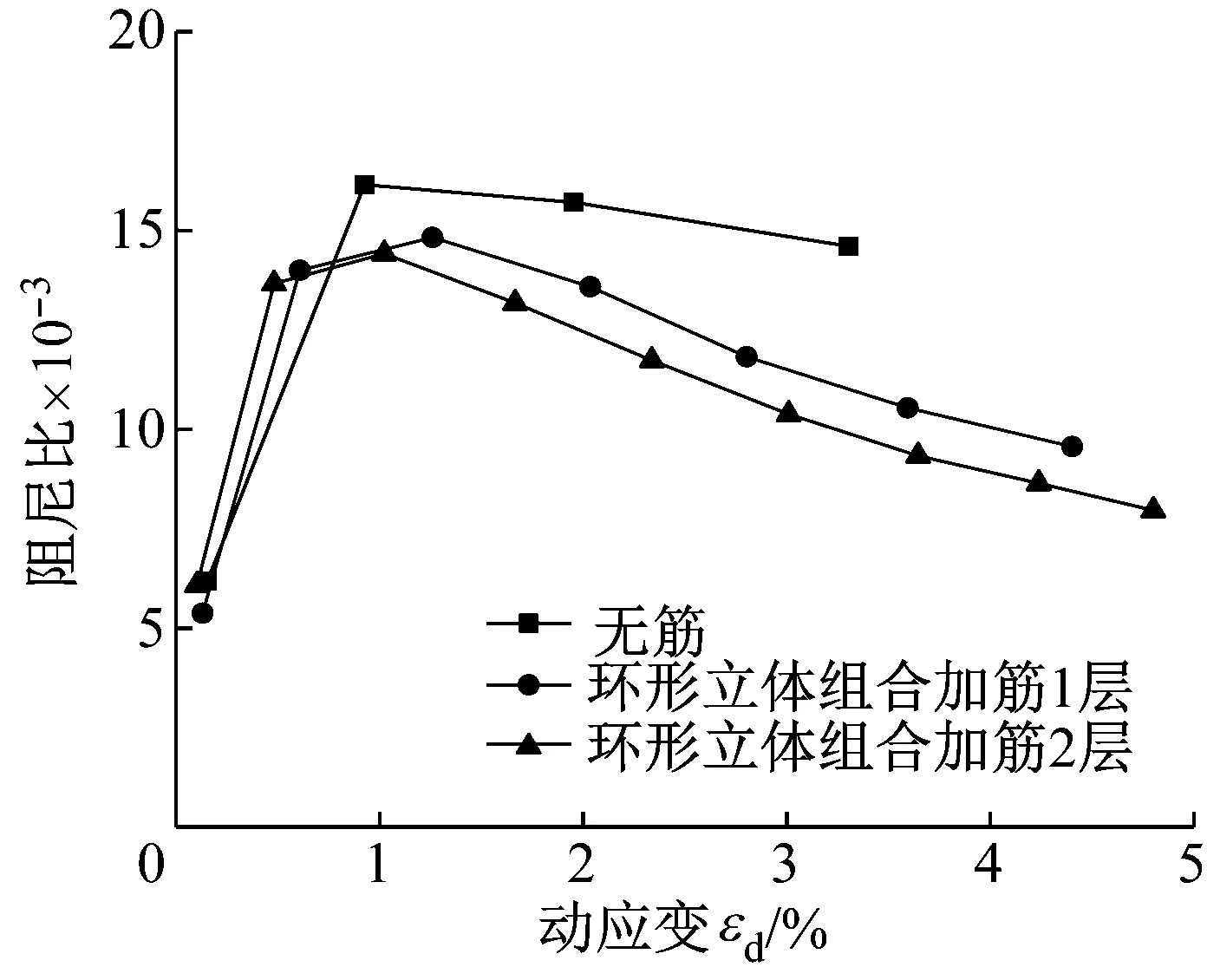
图7 环形立体组合加筋试样阻尼比-动应变曲线
2.1.3 试验围压
不同围压下单层环形立体组合加筋试样的阻尼比-动应变曲线,如图8所示。由图8可知,环形立体组合加筋试样的阻尼比随着围压的增大而减小。与围压为25 kPa时相比,围压为50 kPa时,环形立体组合加筋试样的最大阻尼比减小了11.0%,围压为75 kPa时最大阻尼比减小了16.4%。这是由于围压增大,砾性土试样受到的侧向约束增大,土体更易趋于密实状态,振动波在试样内部沿土骨架传播的路径增多,在孔隙中的传播路径减小,而与土骨架相比,振动波在水中的耗能更大,故密实状态下能量损耗减少,阻尼比减小。
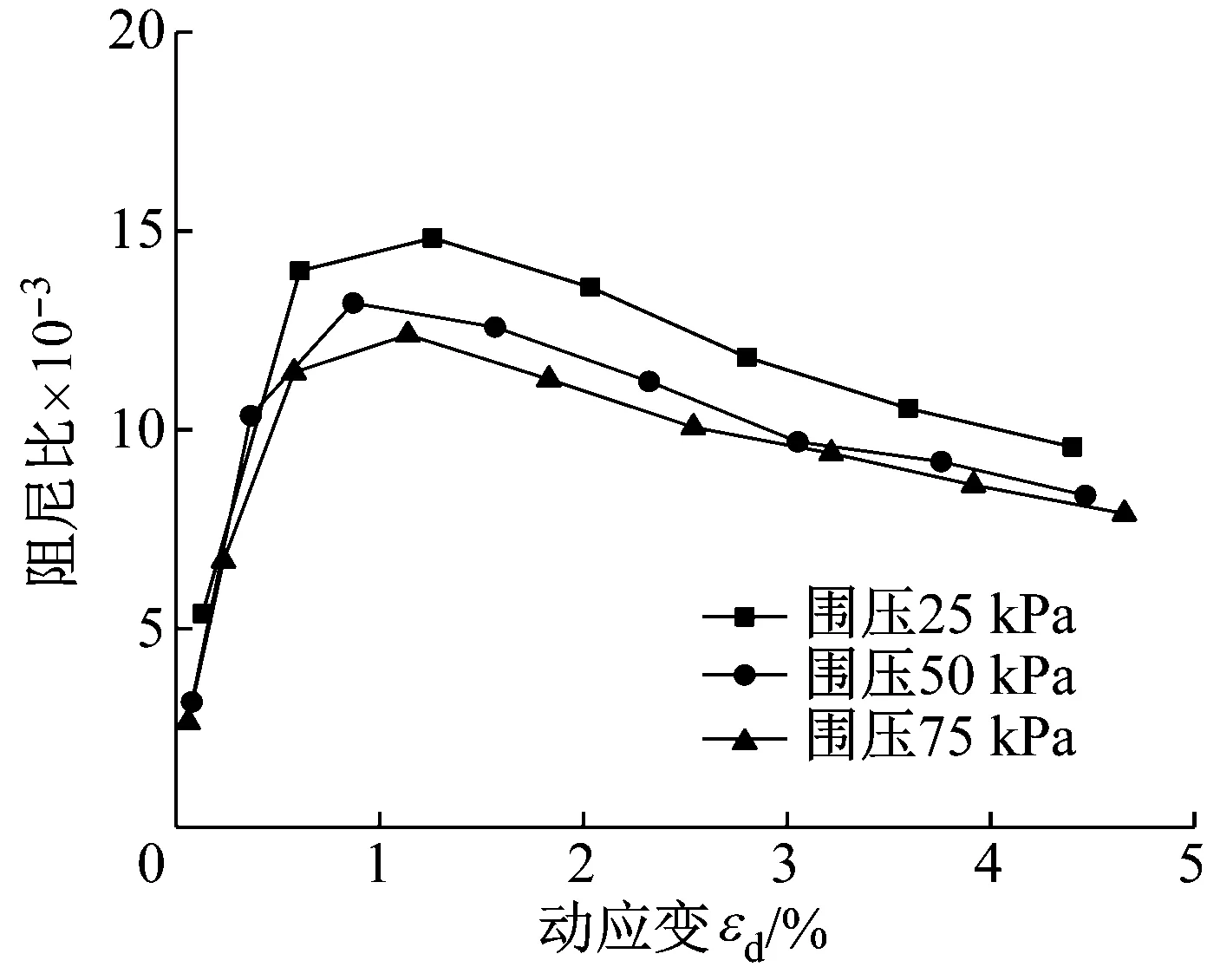
图8 不同围压环形立体组合加筋试样阻尼比-动应变曲线
2.2 骨干曲线分析
2.2.1 加筋形式
将不同循环的滞回圈顶点连线,得到不同应力循环的最大动剪应力和最大动剪应变的关系曲线,称为骨干曲线,是建立土体动本构模型的重要依据。以每级循环荷载第10个循环为代表,将该循环的滞回圈顶点连线,得到多级循环荷载下加筋砾性土的骨干曲线。图9为围压25 kPa下不同加筋形式砾性土试样的骨干曲线。由图9可知,无筋加筋试样承受的试验最大动应力幅值为350 kPa,平铺和环形竖向加筋试样的试验最大动应力幅值为450 kPa和550 kPa,而环形立体组合加筋试样的承载能力最强,所能承受的试验最大动应力幅值为650 kPa,为无筋试样的1.86倍。
目前学者对于土体骨干曲线已有不少研究成果,其中Hardin-Drnevich双曲线模型因形式简单、参数较少而被广泛应用[25-26],其具体计算如式(21)所示
(21)
式中:σd为滞回曲线上的最大动应力;εd为对应的最大动应变;a、b为试验参数;a可表示为试样初始弹性模量的倒数1/E0;b可以表示为骨干曲线最大动应力的倒数1/σy。
将图9中的试验数据进行Hardin-Drnevich双曲线模型拟合,具体结果如表2所示。由表2可知,不同加筋形式下的加筋砾性土试样的决定系数R2均大于0.95,拟合度较高,说明加筋砾性土的骨干曲线适用于Hardin-Drnevich模型。且随着加筋形式的变化,参数a、b的数值均开始下降,即随着加筋形式的变化,加筋砾性土试样的初始回弹模量和骨干曲线的最大动应力增大,这与试验结果中初始回弹模量和骨干曲线最大动应力变化规律相一致。
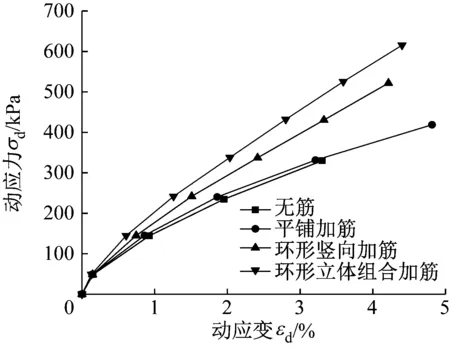
图9 不同加筋形式试样骨干曲线

表2 不同加筋形式试样的Hardin-Drnevich模型参数
2.2.2 加筋层数
围压25 kPa下不同加筋层数的环形立体组合加筋砾性土试样的骨干曲线,如图10所示。由图10可知,增加筋材层数能明显提高试样的承载力,无筋试样承受的试验最大动应力幅值为350 kPa,1层环形立体组合加筋试样的试验最大动应力幅值为650 kPa,2层环形立体组合加筋试样所能承受的试验最大动应力幅值为850 kPa,为无筋试样的2.43倍。
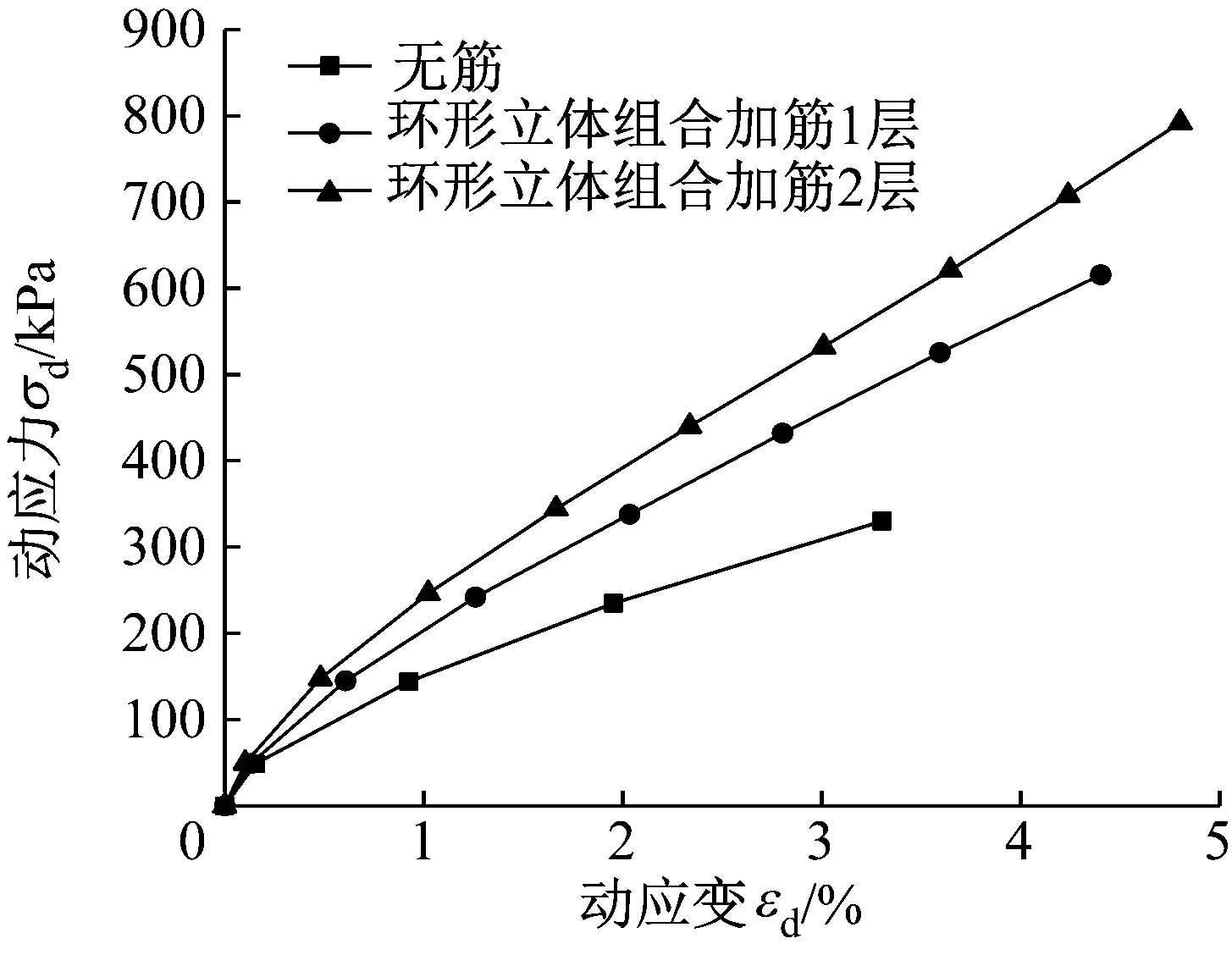
图10 不同环形立体组合加筋层数试样骨干曲线
使用Hardin-Drnevich模型对图10中的试验数据进行拟合,具体拟合结果如表3所示。从表3中发现,Hardin-Drnevich模型参数a、b与加筋层数n之间存在函数关系,分别将参数a、b与加筋层数n进行拟合分析,发现参数a与加筋层数n之间存在线性函数关系,参数b与加筋层数n之间存在指数函数关系,如式(22)、式(23)所示,具体拟合情况如图11所示。说明通过Hardin-Drnevich模型,并结合式(22)和式(23)能够很好的描述加筋层数对加筋砾性土试样动应力与动应变关系的影响。
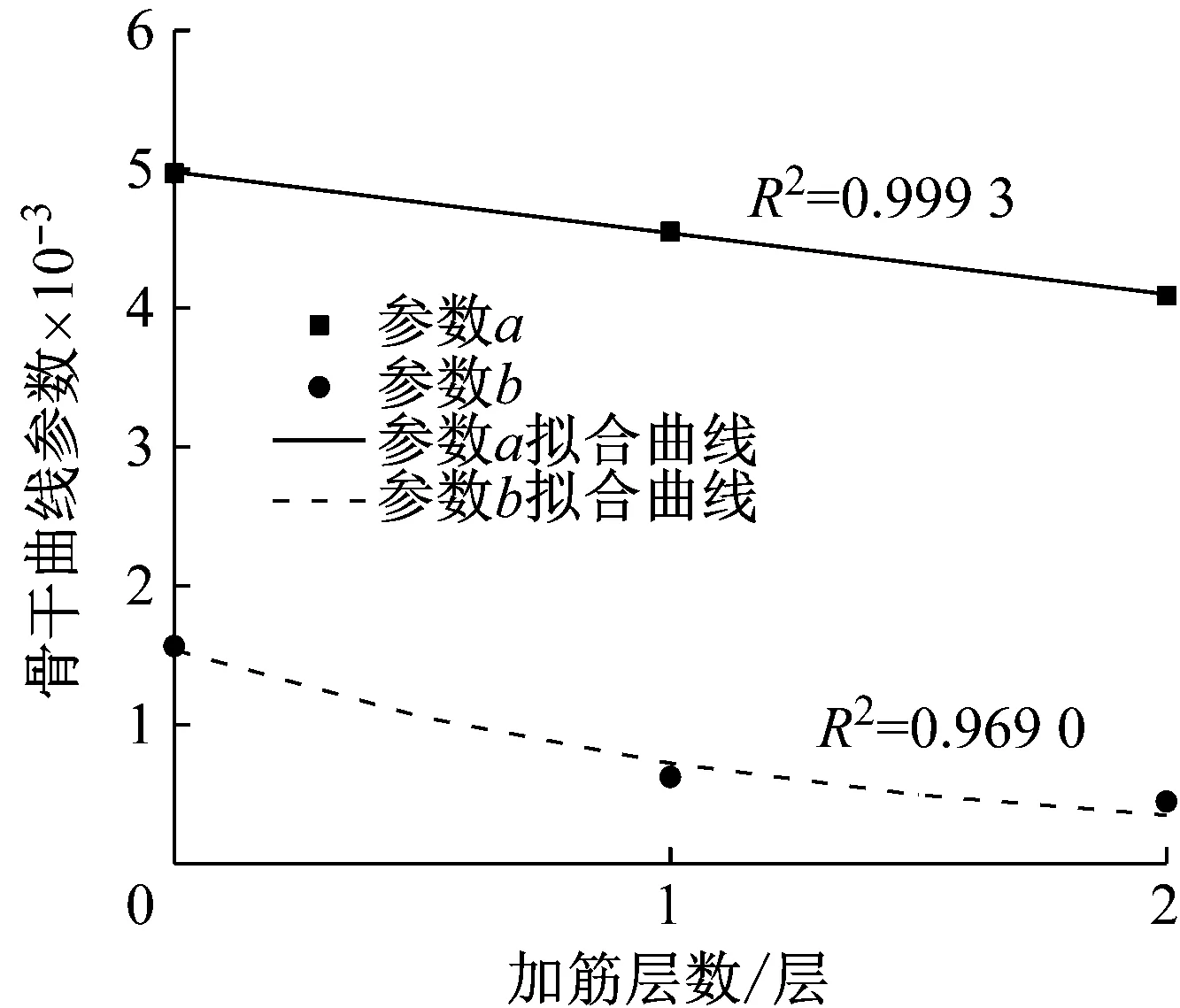
图11 试样Hardin-Drnevich模型参数与加筋层数的关系曲线

表3 不同加筋层数试样的Hardin-Drnevich模型参数
a=-4.40×10-4n+4.98×10-3
(22)
b=1.54×10-3e-0.755n
(23)
2.2.3 试验围压
不同围压下单层环形立体组合加筋砾性土试样的骨干曲线,如图12所示。由图12可知,当围压为25 kPa时,环形立体组合加筋砾性土试样承受的试验最大动应力幅值为650 kPa,当围压为50 kPa时,试样承受的试验最大动应力幅值为750 kPa,当围压为75 kPa时则为850 kPa,在高围压条件下,环形立体组合加筋试样的承载能力要高于低围压条件下的加筋试样。这是因为高围压条件下试样受到较大的侧向约束,砾性土颗粒之间及颗粒与筋材之间的摩擦咬合程度更高,试样在受到竖向的动应力时土颗粒之间的相对错动程度较低,动应变较小,承载力提高。
使用Hardin-Drnevich模型对图12中的试验数据进行拟合,具体拟合结果如表4所示。参照加筋层数对Hardin-Drnevich模型参数的影响分析, Hardin-Drnevich模型参数a、b与围压σ3之间也存在类似的函数关系,分别将表4中的参数a、b与围压σ3进行线性和指数拟合分析,拟合结果如式(24)、式(25)所示,具体拟合情况如图13所示。

表4 不同围压下立体加筋试样Hardin-Drnevich模型参数

图12 不同围压下环形立体组合加筋试样骨干曲线
a=-4.18×10-5σ3+5.55×10-3
(24)
b=6.60×10-4e-2.52×10-3σ3
(25)
通过对骨干曲线的分析,发现Hardin-Drnevich模型适用于加筋砾性土,且Hardin-Drnevich模型参数a与围压σ3和加筋层数n之间存在线性函数关系,参数b与围压σ3和加筋层数n之间存在指数函数关系。于是将加筋层数和围压进行综合考虑,以加筋层数n和围压σ3为自变量,以参数a、b为因变量,分别进行线性和指数拟合,得到能够用加筋层数n和围压σ3求得Hardin-Drnevich模型参数a、b的关系式,如式(26)、式(27)所示,其决定系数R2分别为0.99、0.95。
a=-4.40×10-4n-4.22×10-5σ3+
6.02×10-3
(26)
b=1.45×10-3e-0.78n+10e-0.45σ3
(27)
将式(26)、式(27)代入式(21)中,便得到能够描述不同围压和加筋层数下环形立体组合加筋试样骨干曲线的动应力-动应变方程,如式(28)所示
(28)
式中:a1=-4.40×10-4;a2=-4.22×10-5;a3=6.02×10-3;b1= 1.45×10-3;b2=-0.78;b3=10;b4=-0.45。以围压75 kPa单层环形立体组合加筋工况为例验证该骨干曲线的准确性,结果如图14所示,求得其决定系数R2=0.96,准确性较高。且该骨干曲线模型与Hardin-Drnevich模型相比,能够更好地体现不同埋深的环形立体组合加筋砾性土在循环荷载作用下的动应力-动应变的变化特性,更符合实际情况。
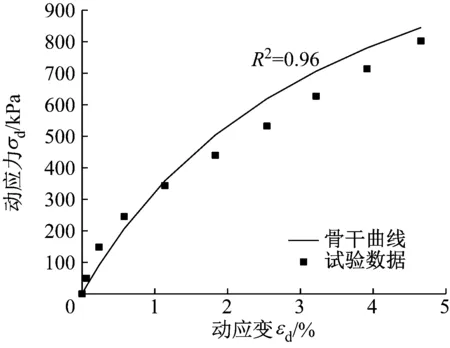
图14 围压75 kPa单层环形立体组合加筋工况骨干曲线对比图
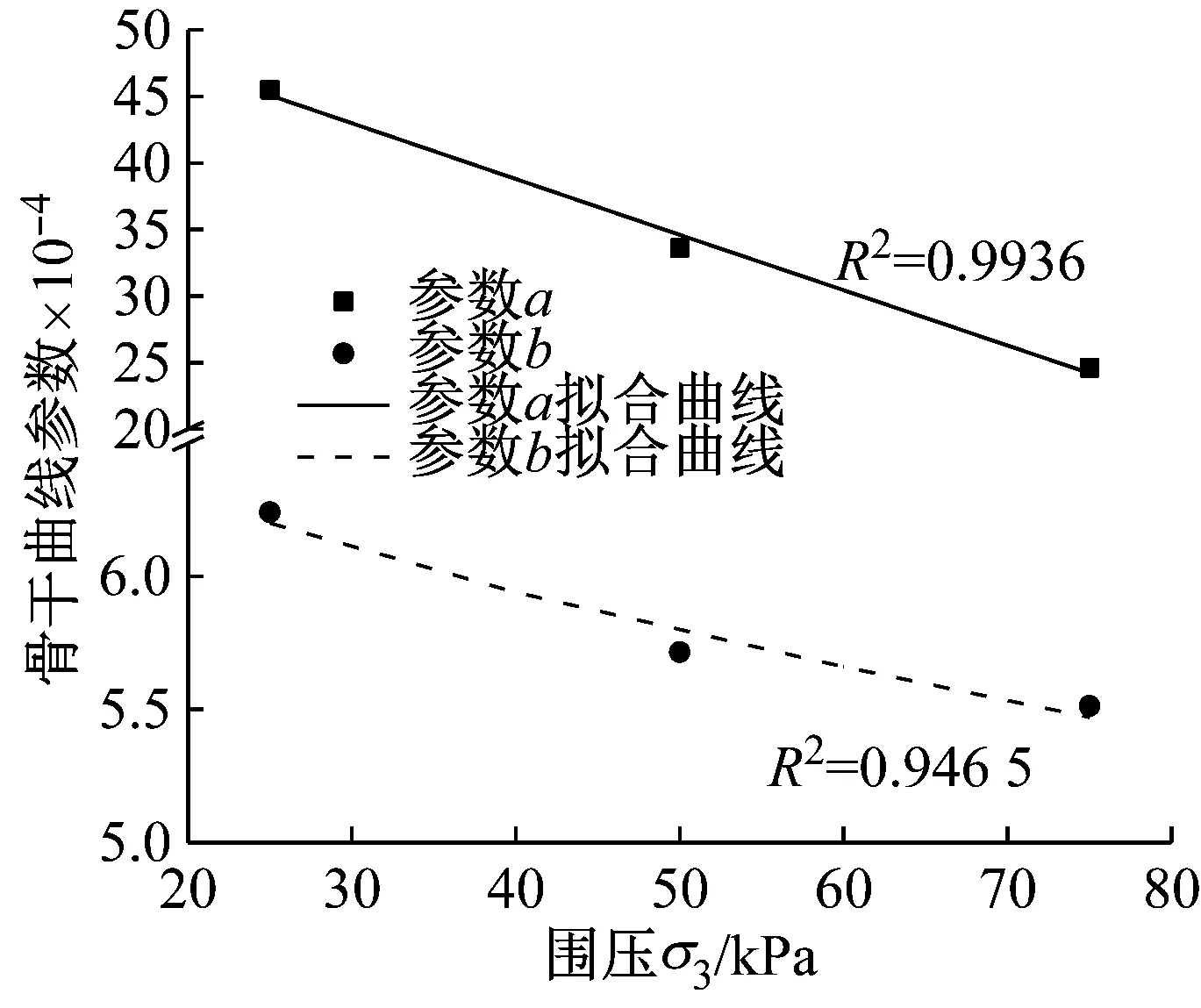
图13 试样Hardin-Drnevich模型参数与围压的关系曲线
Fig.13 The relation curve between parameters of Hardin-Drnevich model of specimens and confining pressure
3 结 论
(1) 通过半正弦循环荷载下输入土体的总能量和损耗能量及土体滞回圈面积的计算,可推导出半正弦循环荷载下动三轴试验中试样阻尼比的计算公式。
(2) 多级循环荷载下砾性土试样的阻尼比呈现前期增大随后减小的规律,阻尼比在动应变达到1%左右达到峰值。
(3) 加筋减少了砾性土试样的阻尼比,其中环形立体组合加筋砾性土试样的阻尼比最小,并随加筋层数和试验围压的增大而减小。
(4) 验证了Hardin-Drnevich模型适用于加筋砾性土的骨干曲线,并提出能够反映围压和加筋层数影响的环形立体组合加筋砾性土骨干曲线方程。
