基于PSO-GPR的数控机床热误差建模及泛化性研究*

张 蕾 黄美发 陈 琳 杨瑞兆

(①玉林师范学院物理与电子信息学院,广西 玉林 537000；②桂林电子科技大学机电工程学院,广西 桂林 541004；③广西大学机械工程学院,广西 南宁 530004)

在加工过程中，数控机床的总误差主要由几何误差、力误差和热误差等组成，而因发热造成的机床加工热误差可高达70%左右[1]。经过专家学者多年的研究，先后建立了多种机床热误差模型，比如支持向量机(SVM)、神经网络、有限元模型、最小二乘支持向量机等[2-5]。其中最小二乘支持向量机模型在预测非线性小样本的回归问题上有较高的精度，如林伟青、傅建中等建立的最小二乘支持向量机热变形补偿模型[6]，可实时反馈新数据以调整模型，有效减小了热误差对精度的影响。张宏韬、杨建国等[7]将模糊逻辑算法和神经网络相结合，构建模糊神经网络热变形补偿模型，经实验对比，具有较高的预测精度，但对模型的泛化性研究较少。

而高斯过程回归(GPR)是近几年研究出来的一种机器学习回归方法[8-9]，其主要基于贝叶斯框架下的统计学理论基础，在求解非线性、小样本和高维度等回归问题中有较强的泛化能力，且适应性良好。为研究高斯过程回归在数控机床热误差建模中的应用，结合粒子群算法(PSO)，建立PSO-GPR热误差模型，即在GPR模型的迭代训练时，利用粒子群算法在全局范围内对其搜索最优超参数。与未经优化的GPR模型比较，PSO-GPR模型对热误差的预测精度更高。

1 基于PSO优化参数的GPR算法

1.1 高斯过程回归

GPR是一种基于贝叶斯理论和统计学习理论相结合的非参数模型，其定义主要由输入X处的均值函数m和协方差函数k[10]。假定机床温度输入与主轴产生的热误差作为输出之间的关系f为高斯过程，则f～GP(m,k)。

对于训练集D={(Xi,yi)|i=1,2,...,n}，其中Xi和yi分别表示第i个输入向量和目标输出。构建回归模型：

y=f(X)+ε

(1)

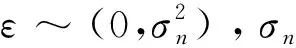
对于输入向量X={X1,X2,...,Xn}，假设f(Xi)服从高斯分布，则f(X)服从多元高斯分布：

f(X)～N(m(X),K)

(2)

式中：m(X)为均值向量，K为协方差矩阵。

(3)

通常通过数据预处理使均值函数m(X)=0：

(4)

f*～N(0,K*)

(5)

训练集D的输出值y与预测集P的输出f*服从多元联合高斯分布，则联合先验分布为：

(6)

式中：K*=[k(x*,x1),…,k(x*,xn)]，K**=k(x*,x*)。

根据多元高斯分布的条件分布形式，可得f*的后验证分布为：

f*|X,y,X*～N(m(f*),cov(f*))

(7)

(8)

(9)

经过多个核函数对比寻优，这里选择平方指数协方差函数即：

(10)

高斯过程回归使用了贝叶斯技巧，得到的模型属于非参数概率模型。在数控机床热误差补偿问题中，GPR可理解为在每个测量的热变形的点上进行收束，在点与点的间隔中进行一定概率的扩散，这使得GPR可以在热误差回归问题中具有较好的适应性和泛化性。

1.2 PSO-GPR模型

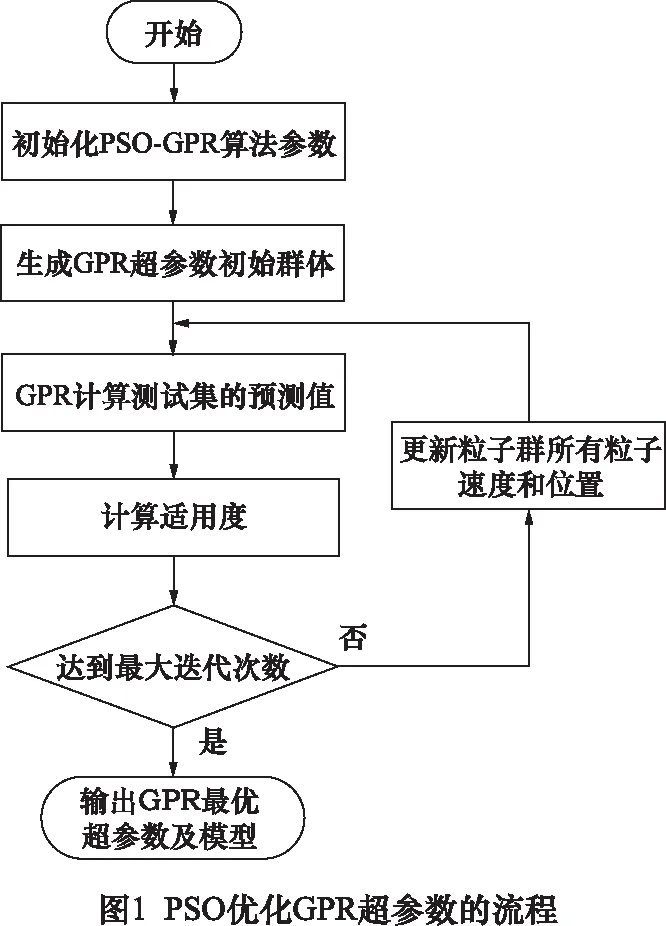
在高斯过程回归训练过程中，通过粒子群优化算法，对GPR的超参数在训练数据的全局范围内进行寻找最优解，从而使PSO-GPR热误差模型的均方误差MSE达到最低，PSO优化超参数步骤如图1所示。在此需要随机生成包括粒子群规模、惯性权重、超参数搜索区间、最大迭代步数和超参数等的GPR模型初始化粒子群初始参数值。其中训练样本为数控机床热误差测量实验中所测得的温度变化量和热误差变化量。

2 机床主轴热误差测量与建模

2.1 机床主轴热误差测量实验

以某型号数控车床为研究对象，首先通过对数控车床进行热分析，并将10各关键测温点分别布置在车床主轴、电机和变速箱等位置，具体测温点布置如表1所示。将测量的温度数据，利用聚类的方法[12]优化测温点，并以测温点4、7、10的温度变化量θ4、θ7、θ10作为热误差建模的3个输入量。

表1 温度传感器布置

实验采用电涡流位移传感器对主轴Z方向和X方向进行热变形采集，其分辨率为0.01 μm。因车床主轴径向和轴向的热变形补偿原理相同，在此只取主轴轴向Z方向的热变形进行研究。设置电涡流位移传感器如图2所示。

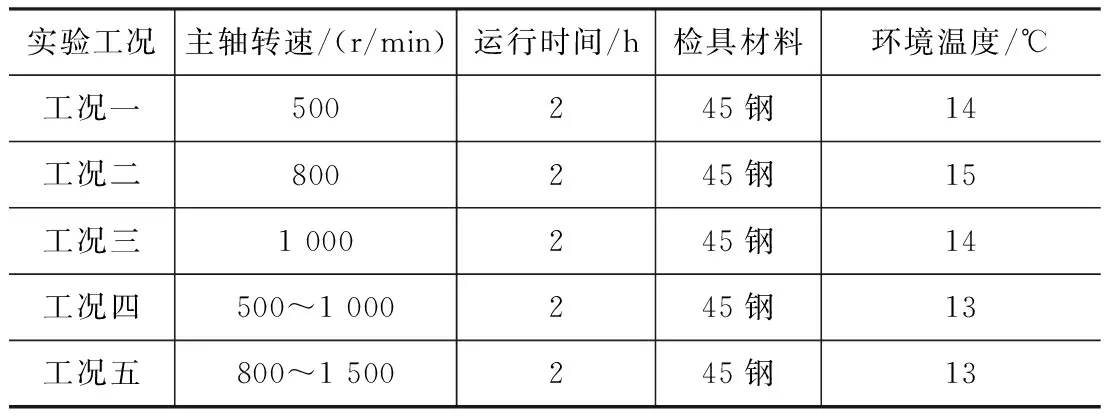
表2 数控车床的工况

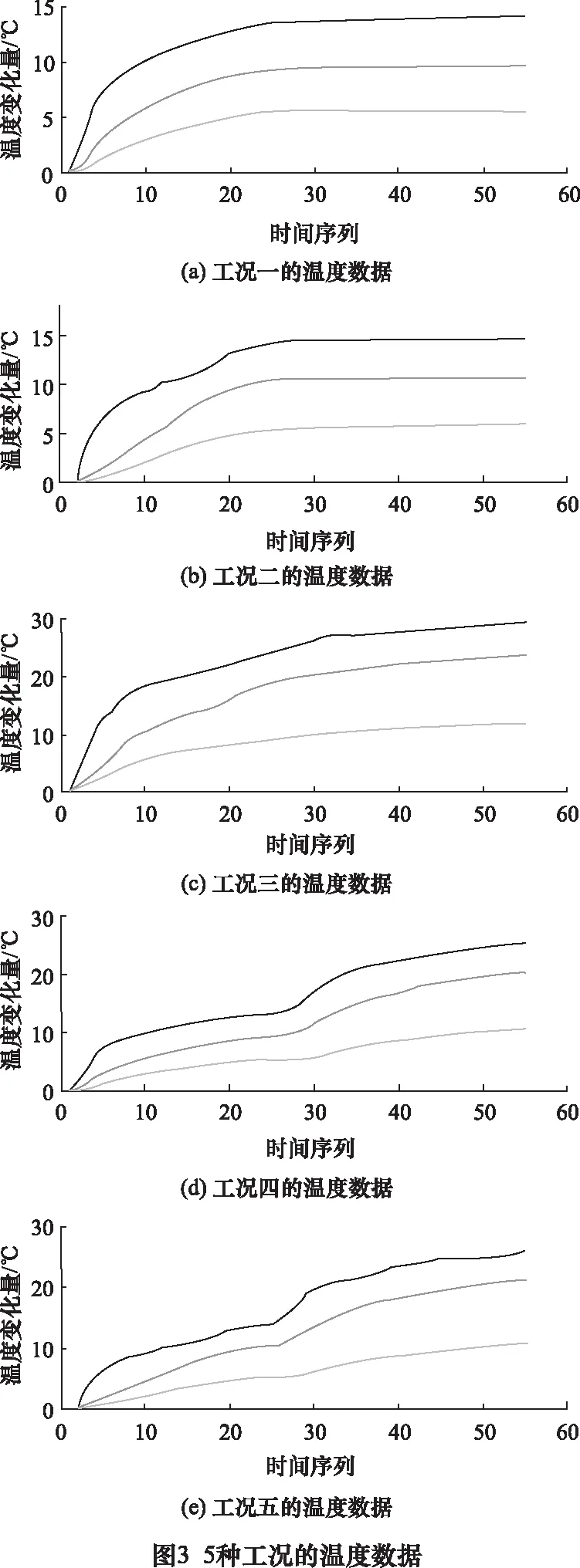
测量采集表2所示的5种工况温度与热误差变形量数据，其中工况一、二、三均以不同的主轴转速由车床冷态空载恒速运行2 h达到车床热平衡；工况四为车床冷态以主轴500 r/min运转1 h后，切换1 000 r/min运转1 h到车床热平衡；同样，工况五则是从800 r/min转速运行1 h再以1 500 r/min转速运行1 h达到热平衡。系统采集热误差和温度值的时间间隔为2 min，经数据处理得，5种工况的温度及热变形量如图3、图4所示。

2.2 PSO-GPR热误差建模结果的分析与比较

为研究PSO-GPR热误差模型的预测精度，以工况三测量值作为模型训练数据，其中测量的温度变化量为模型的输入，轴向热变形量为模型的输出，通过粒子群优化算法对高斯过程回归的超参数迭代搜索最优值。训练数据均分为5个集合，并相互进行交叉验证，以防止模型发生过拟合。

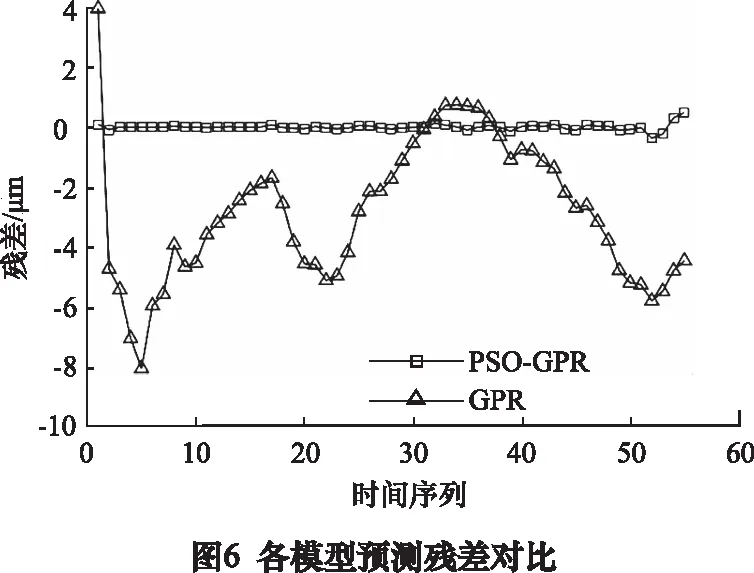
以未经优化的GPR模型作对比，两个模型的热误差预测结果及其残差如图5、6所示，PSO-GPR热误差模型与实际测得的热误差值十分贴合，其最大残差为0.49 μm，均方根误差RMSE为0.11 μm。而未经优化的GPR热误差模型预测最大残差为8.08 μm，均方根误差RMSE为3.68 μm。可见PSO-GPR热误差模型预测精度更高。

2.3 数据增强的PSO-GPR热误差模型泛化性研究

在实际加工中，数控机床要在多种不同的工况下进行切换作业，所以热误差补偿模型就需要保证能在多种工况和条件下进行有效地热误差补偿，而这与模型的泛化性能息息相关。在机器学习领域，回归模型泛化性能的提高，除了对回归模型自身进行参数和结构的优化外，训练数据增强即数据特征的扩展和补充也是其提高泛化性的重要途径。

针对GPR自身计算量较大而要求训练样本量不能过多的特点，为了能使训练后的PSO-GPR模型不仅可以充分反映温升与热变形的关系，又要对机床其他工况下的数据特征进行学习，所以建模时的训练数据需对其他部分工况的数据进行一定的补充增强，以提高模型泛化性能。

将工况四、工况五作为验证数据，分别对以工况一、工况二和工况三为训练数据的PSO-GPR和仅以工况三为训练数据的PSO-GPR热误差模型进行预测。测试结果如图7～10所示。需要说明的是，若仅以工况一或工况二作为训练数据，训练的热误差模型会出现过拟合的情况，即无法对工况四、工况五进行预测，导致此结果的原因是工况一和工况二的最大热平衡误差值并不是全局的最大热平衡误差值，训练出来的模型并不能预测更高温度工况的热误差数据。

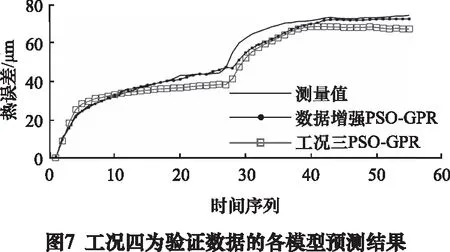
从验证结果可知，以工况一、工况二和工况三为训练数据的PSO-GPR热误差补偿模型预测结果更贴合工况四、工况五的真实数据，比以单一工况作为训练数据PSO-GPR模型具有更好的泛化能力，最大残差分别下降了35%和33.7%。具体模型泛化性对比如表3所示。

表3 两种模型的泛化性对比

3 结语

以某种通用的数控车床进行热误差补偿研究，通过实验采集5种工况下的温度与热变形量，并以粒子群算法优化的高斯过程回归热误差模型进行热变形量补偿，经实验对比，得到如下结论：

(1)基于统计学习理论的高斯过程回归以其高维数、小样本、模型参数少等特点可以对数控机床热误差补偿问题进行有效地预测，且经过粒子群优化参数的GPR热误差模型预测精度更高，训练数据预测最大残差从8.08 μm下降到0.49 μm。

(2)单样本的模型还未能充分反映其他条件下(环境温度、工况等)的热误差变化，此时可通过模型自身参数寻优和更多数据样本的特征学习来增强热误差模型的泛化能力。经过数据增强的PSO-GPR模型学习了3个工况的数据特征后，在以工况四、工况五的数据验证下，比工况三的PSO-GPR模型的预测精度更高，泛化能力更好，最大残差分别下降了35%和33.7%。