具有非线性时间依赖持有及缺货成本的变质品库存控制研究*

□ 李书慧，罗治洪

(昆明理工大学 管理与经济学院，云南 昆明 650000)

1 引言

变质型产品如蔬菜鲜果的腐烂和液体的挥发并不是匀速发生的，通常是随着持有时间的增加而加快的。在存储过程中，零售商为了防止蔬菜鲜果等产品的腐烂和液体的挥发会根据持有时间的增加而花费更多的成本以保持产品的新鲜程度。另外，对于变质型产品通常需要进行积压以避免因变质产生更大的成本。当缺货发生时，消费者被认为是没有耐心的且下一次补货的等待时间成为消费者是否接受积压的决定性因素。

库存控制中的时间依赖成本主要体现在持有成本的变动、缺货时滞后供给成本、机会成本和采购价格的变动。时间依赖在库存控制方面的研究主要集中在时变需求，具有时间依赖特征的成本和价格的变动。Kucuk[1]对土耳其不同规模的零售店进行调查后发现，缺货成本是由消费者对于缺货的反应所决定的，且消费者的反应主要是由于对品牌或商店忠诚度和缺货等待时间所刺激的。Tsao和Sheen[2]开发了一个考虑批量大小、时间依赖的采购成本和信用期可变的变质物品库存模型，其中单位采购成本是关于补货周期的线性函数。Mishra等[3]考虑了一个需求、持有成本和变质率均为时间依赖的库存模型，其中持有成本是关于存储时间的线性增函数。Alfares[4]认为在库存系统中，需长期储存的物品通常需要更先进或昂贵的设施来维持，因此，提出了一个适用于不同存储时间范围的持有成本递增阶跃函数和采购成本是订单批量的递减阶跃函数的库存控制模型。

变质品库存研究已经成为库存控制中的热门领域。目前，对于变质品的变质过程描述主要有以下三种。

①目前大部分研究认为库存随着时间以不同的方式衰减且单位时间的持有成本是固定的，累积持有成本是关于时间的线性增函数。

②不单独体现变质品的变质率，而是将变质放在持有成本中一同考虑。Weiss[5]首次提出非线性持有成本库存系统，其中非线性增加的持有成本是随着物品老化而产生的销售损失。Ferguson等[6]在Weiss的基础上提出有两种情形造成凸持有成本：a.非线性持有成本的增加是由于用变质或老化的产品来满足需求可能需要进行降价或丢弃处理而造成销售损失；b.变质性产品每天损坏的单个产品百分比随着变质而增加，变质或老化也可看作是非线性持有成本。Sazvar等[7]考虑了一个具有可变提前期且非线性持有成本依赖于储存时间、短缺完全延期的库存模型，以确定最优价格及补货周期。Edalatpour和Al-e-Hashem[8]建立了一个持有成本依赖储存时间的变质性产品的互补和替代的定价库存模型，试图获得最优价格和补货周期。Pando等[9]假设持有成本是与储存时间和库存数量相关的非线性函数，目标是盈利能力比率最大化。

③同时考虑库存随着时间衰减和非线性持有成本函数。Giri等[10]提出了一个变质性物品库存模型，其中变质率是恒定不变的，持有成本被视为与储存时间和库存数量相关的非线性函数。

在现有的延期交货及其损失的库存文献中，缺货成本可概括为三种类型[11]。第一种，每单位积压需求的成本都是不变的(不受等待时间的影响)；第二种，每单位积压需求的成本与等待时间呈正相关(不考虑缺货的数量)；第三种，缺货成本受缺货数量和等待时间的共同影响，以恒定的比例增加。Montgomery和Johnson[12]是第一个提出部分延期交货概念的，并且认为每单位缺货的成本是固定的，总缺货成本随缺货时间线性增加。Abad[13]考虑了具有部分延迟订购的易腐品库存模型，其中滞后供给率是以顾客没有耐心的方法表示的，并且根据顾客对等待时间的敏感程度分别采用线性函数倒数和负指数函数。San Jose等[14]在Montgomery的基础上，提出缺货时需求是等待时间的负指数函数，其中缺货成本包括一个固定成本和一个与缺货时长成比例的成本。Sicilia等[15]考虑缺货时需求率是关于等待时间的线性函数且缺货成本是缺货时间的二次函数。罗兵等[16]在特价商品的研究中提出，在缺货时特价商品的价格和等待时间共同决定了滞后供给率。罗兵等[17]以连锁商店为对象，研究顾客等待时需求转移的情况，其中滞后供给率是关于等待时间的负指数函数，缺货成本依赖等待时间的成比例增长。

本文与过去文献的主要区别在于：①对变质品的研究中，绝大多数的学者采用库存以一定的速率衰减，单位时间的持有成本是固定的。本文用非线性持有成本来考虑变质品的变质或挥发特征，累积持有成本呈指数函数增加。②对于将变质率放在持有成本中考虑的文章，极少有研究涉及滞后供给情况。Sazvar等[7]考虑了一个完全延期供给的库存模型，本文在其基础上建立了一个部分滞后供给的库存模型。③本文与大部分固定的单位缺货成本不同，采用依赖于等待时间的非线性缺货成本。基于以上三点区别，建立一个具有时间依赖特征的非线性持有及缺货成本的库存控制模型。

2 具有时间依赖成本的库存控制模型

当零售商销售变质品时，通常会面临变质品的变质率随存储时间呈指数型增长，且为了降低产品变质带来的损失，一般会允许产品部分积压的问题。为了解决变质所带来的问题，需要对具有时间依赖特征的变质品进行库存控制研究。本文以单位时间总利润最大化为目标，通过构建库存控制模型，得到库存决策中有现货时间、缺货时间和回补订购数量等最优解。

2.1 符号定义和假设条件

为了描述问题和建立模型，令市场需求率D是确定且已知的；Ps、Pb分别为每单位商品的销售价格和采购价格(Ps>Pb)；单周期长度为T=t1+t2，其中t1、t2分别为有现货时间和缺货时间长度；最大库存水平为S；最大滞后供给量为B；A为固定的订货成本/次；w、π分别为滞后供给成本和机会成本(w<π)；h为单位商品持有成本。为了简化问题，假设瞬时补货；提前期为零。

变质品因腐烂而质量下降，无形变质产品因放射、蒸发等问题需要更好的存储设施，因此变质品的每单位时间持有成本不是固定的。参照文献[7]，令单位商品t时间内的累积持有成本H(t)=htγ,其中γ为持有成本弹性(γ>1)。γ表示零售商为了维持产品的新鲜程度每单位时间所花费的保鲜费用。

2.2 库存控制模型

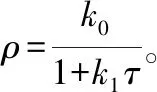
图1 单周期内商品库存水平

商品在单周期内的库存变化可用如下微分方程表示：

(1)

由边界条件I(t1)=0，可得库存水平为

(2)

(3)

商品单周期内的总利润TR由总销售收入SR、总回补成本AC、累计持有成本HC、滞后供给成本BC和机会成本LC构成，具体如下：

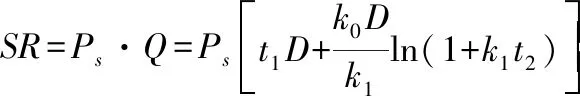
可得商品单周期内的单位时间总利润ATR(t1,t2)：

ATR=(t1+t2)-1TR=(t1+t2)-1

(4)

在t1>0、t2≥0的条件下，库存控制模型的优化目标是：

(5)

2.3 模型的最优解分析

ATR=(t1+t2)-1

(6)

对式(6)关于t1、t2求偏导数，并根据最优解存在条件令其为零。可得：

(7)

(8)

联立式(7)和式(8)可得：

(9)

令上式右边为f(t2),即

(10)

对f(t2)关于t2求导可得：

(11)

由式(9)可得t1关于t2的表达式，记为t1(t2)：

(12)

对t1(t2)关于t2求导可得：

(13)

令式(8)左边为F(t2)，并将式(6)代入可得：

(14)

可根据F(t2)的性质分析该商品的库存问题。

当t2趋于0时，得：

当t2趋于∞时，得：

3 数值分析

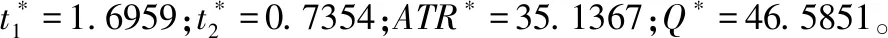
以下对持有成本弹性、等待时间敏感因子、等待时间的短缺滞后量供给敏感因子参数进行灵敏度分析，其它参数取值同上。

3.1 持有成本弹性对最优决策的影响

表1 持有成本弹性灵敏度分析

从表1可知，随着γ的增大，最优缺货时间随之增加；最优有现货时间、回补数量及单位时间总利润随之减少。γ是非线性持有成本弹性，当γ增加时，也可理解为该产品的变质或挥发速度加快，同时意味着为了维持每单位产品的新鲜程度，延迟其腐烂或挥发的速度需要增加更多的保鲜储存成本。因此，在其他条件不变的情况下，特别是当滞后供给成本在一定范围内时，倾向于保持较少的库存水平，避免较高的持有成本。

3.2 等待时间敏感因子对最优决策的影响

表2 等待时间敏感因子灵敏度分析

从表2可知，随着等待时间敏感因子k1的增加，最优有现货时间、最优回补订购量均随之增加；最优缺货时间和单位时间总利润均随之减少。这是因为等待时间敏感因子k1的增加意味着消费者对于等待的不耐烦程度越高，即对待等待时间更加敏感。当k1增加时，有更多的消费者放弃等待选择购买替代品或转向其它零售店。因此，在这种情况下，应增加回补订购量以保证满足更多的需求，减少缺货需求。

3.3 等待时间的短缺滞后供给量敏感因子对最优决策的影响

表3 等待时间的短缺滞后供给量敏感因子灵敏度分析

从表3可知，随着等待时间的短缺滞后供给量敏感因子k0的增加，最优有现货时间减少；最优缺货时间、最优回补订购量和单位时间总利润都随之增加。k0的增加意味着消费者对于等待滞后供给的意愿提高，对等待时间并不十分敏感，因而消费者不会产生放弃购买、选择其它零售商购买或者购买替代品的行为。所以，在等待时间的短缺滞后量供给敏感因子k0增加，其它条件不变的情况下，零售商可以选择饥饿营销的手段，缩短有现货时间以减少持有成本，适当延长缺货时间，以达到更高的利润。

4 结论

本文使用非线性成本体现变质品的腐烂和非变质品的挥发，当进入缺货期后，用顾客不耐烦函数表示滞后供给率体现等待时间对消费者等待意愿的影响，产生的缺货成本包括滞后供给成本和机会成本。以单位时间总利润最大化为目标，建立相应库存模型。通过对模型的证明和数值仿真分析，得出以下主要结论：①随着γ、k1、w和π的增加，最优单位时间总利润逐渐下降；随着k0的增加，最优单位时间总利润逐渐上涨，其中对单位时间总利润影响重要程度因子分别为：k0、γ、k1、π、w。因此，零售商应更加注重等待时间的短缺滞后供给量敏感因子和持有成本弹性对单位时间总利润的影响，对于高度腐烂的商品应尽可能地缩短其持有时间，以避免过高的持有成本。②随着γ、w、k1和π的增加，最优回补周期T*呈现下降趋势，其含义是非线性持有成本、滞后供给成本、等待时间敏感因子和机会成本均对该产品的回补订货周期产生负影响。因此，零售商应通过缩短补货周期，增加补货频率来满足需求以减少过高的持有成本和缺货成本。③当商品的售价、采购价、等待时间的短缺滞后量供给敏感因子、机会供给成、订货成本和持有成本弹性的比例失衡时，应不允许缺货以达到最高的单位时间总利润。

未来还可以进行后续的深入研究，如考虑短缺发生时滞后供给率是等待时间的其它形式(如：指数、线性等形式)、缺货时提供依赖于等待时间的不同价格折扣策略、订货周期可变等情况。