飞行器气动外形的正交设计与分析
2022-02-22池元成郑小鹏王长庆
池元成, 张 冶, 郑小鹏, 王长庆, 宁 学
(中国运载火箭技术研究院, 北京 100076)
0 引言
飞行器总体设计是根据指标要求,对飞行器及其各系统进行综合、协调、研究和设计的过程,涉及多专业多学科。其中,飞行器气动外形设计尤其重要,在总体设计的初期就要参与,以便为后续专业提供必要的设计输入。
气动学科是飞行器外形设计的核心基础,是总体设计的核心专业,是弹道、载荷、姿控等专业开展设计分析的先决条件之一。在工程设计中,飞行器气动外形往往是以现有飞行器外形为基础,通过合理调整外形参数,分析气动数据(工程算法或CFD计算),再经过多轮次迭代,获得满足设计要求的外形。
在飞行器总体设计的初期,需要快速得到满足要求的飞行器外形,传统的基于代理模型的外形优化,需要在试验设计的基础上,构建代理模型,优化结果依赖代理模型的准确度。构建代理模型时,依托正交试验设计,通过较少的样本点获取训练样本,再构造气动代理模型,往往忽略了数据分析,没有做关键参数的辨识。为实现飞行器参数灵敏度分析及参数分类,利用正交试验设计及方差分析,完成了气动性能的参数灵敏度分析,降低了飞行器设计复杂度。
因此,本文将基于正交试验设计方法分析飞行器气动外形,其试验次数少,方法简单,在快速获得飞行器外形的同时,还能为方案优化提供合理的初值,提高飞行器总体方案论证效率。
1 正交试验设计
正交试验设计(orthogonal design),是利用正交表(orthogonal table)对多因素试验合理安排,并开展科学分析的方法,可通过较少的试验次数获得较为准确的结果,且因其过程简单易掌握,在多个领域中被广泛应用。
正交是利用试验的因素数和因素水平,依据正交原理安排的表格,具有整齐可比性、均衡搭配性的特点。正交表可表示为(),其中为正交表代号,为试验次数。为水平数,为参与试验的因素个数。
正交试验设计的一般步骤为:
1)通过试验目的,确定试验指标,即因素的响应值;
2)选择参与试验的因素及其水平数;
3)根据因素和水平数选择正交表,并完成正交表的表头设计;
4)根据试验结果,填充试验指标数据;
5)结合正交表,对试验结果统计分析;
6)满足试验要求,结束;否则,返回步骤2)。
正交试验结果分析方法有极差分析法和方差分析法。极差分析法简单直观、计算量小,但是不能估计误差的大小;方差分析法考虑试验条件的改变和试验数据存在的试验波动,实现对误差的估计。
2 飞行器气动外形设计参数选取
为了分析某飞行器外形气动设计参数的响应分析,利用图1所示的外形进行正交试验设计。其中,I级长度(1)和直径(1)、II级长度(2)和直径(2)、头部舱长度(3)作为多因素试验因素,单位取mm,用于计算不同条件下的阻力系数。
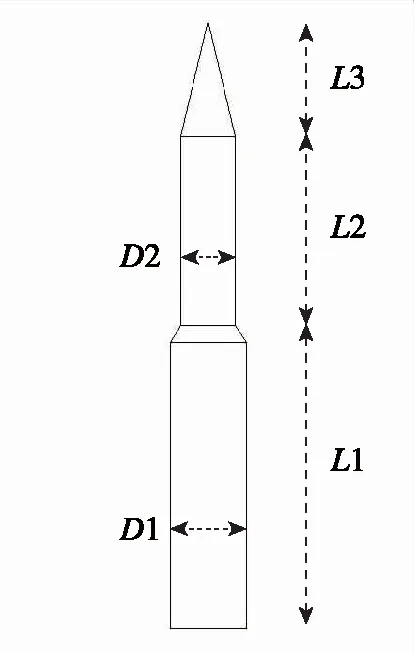
图1 飞行器气动外形Fig.1 Aerodynamic shape
变量说明、取值范围及水平如表1所示。

表1 各变量说明
3 气动外形正交试验设计与分析
对于表1所示的飞行器外形参数列表,考虑试验规模,以及方差分析的需求,根据I级长度(1)和直径(1)、II级长度(2)和直径(2)、头部长度(3)等5个因素,并利用表1中给出的5个水平,采用6因素5水平的正交表作为试验号(5),表头设计和各因子水平如表2所示,并通过CFD计算获得马赫数3时,对应试验的阻力系数值,误差列用于方差分析。
利用表2数据做极差分析,结果如表3所示。
表3中,表示某个试验因素的水平号为(=1,2,…,5)时,所对应的阻力系数之和。=5,表示某一个因素取水平时所得阻力系数的算术平均值。
通过分析各因素之间极差的大小,可以获得不同因素对试验结果的影响程度,即极差越大,说明该因素对阻力系数的影响也大,也就是最主要因素,反之,说明该因素对阻力系数的影响小,也就是非主要因素。由表3可知,极差顺序为
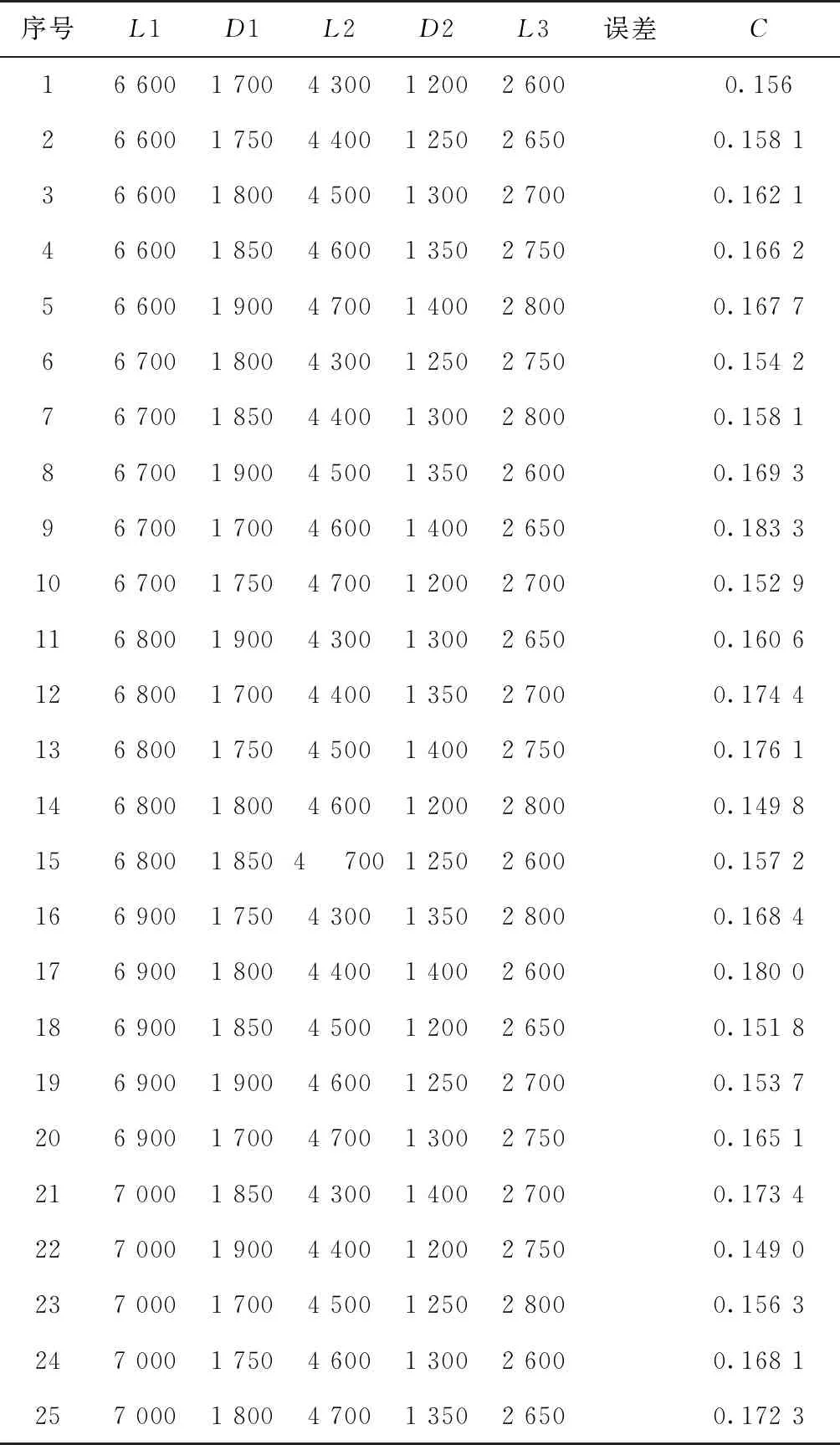
表2 正交试验结果

表3 极差分析结果
=max{,=1,2,…,5}-min{,=1,2,…,5}
或
=max{,=1,2,…,5}-min{,=1,2,…,5}。
2>1>3>1>2,所以各因素从主到次的顺序为:II级直径(2),I级直径(1),弹头舱长度(3),I级长度(1),II级长度(2)。选取影响较大的两个因素II级直径(2)和I级直径(1)分析与阻力系数的关系,如图2所示。

图2 阻力系数关系图Fig.2 Drag coefficient
方差分析可在极差分析的基础上,给出因素的相对量化的比较结果,即对试验结果的显著性影响。通过方差分析可在多组试验之间,分析随机误差引起的波动和水平变化带来的波动。方差分析是通过将阻力系数的总离差平方和分为各因素的离差平方和与随机误差引起的离差平方和,并利用自由度计算平均偏差平方和,最后以检验给出因素的显著影响。根据表3的结果,给出本文的方差分析表,如表4所示。
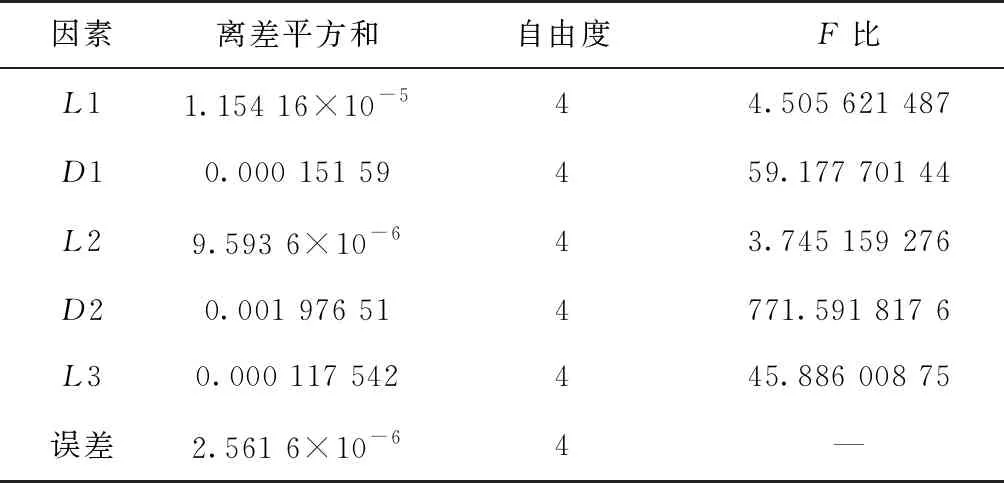
表4 方差分析结果
由表4可知,1,2,3的比值均大于001(4,4)=160,说明1,2,3这3个因素的改变对阻力系数具有很显著的影响,1和2的值小于005(4,4)=639,说明1和2对阻力系数有一定影响。结合表3和表4可知,对于选取的飞行器外形,相对于1和2,2,1和3具有主导性影响。
结合不同因素的优水平与阻力系数的关系,若阻力系数越大越好,则应选择相应的因素水平,即各列中(或)中对应的因素水平;反之,若阻力系数越小越好,则相应选择因素水平即可。对于飞行器外形,阻力系数越小越好,所以挑选每个因素的(或)最小值对应的那个水平,所以,优方案为1=6 600,1=1 900,2=4 300,2=1 200,3=2 800。反之,最大阻力系数的劣方案为1=7 000,1=1 700,2=4 500,2=1 350,3=2 600。
此外,可通过趋势图进行验证,横坐标为因素水平,纵坐标为平均值。各因素的趋势图如图3所示。
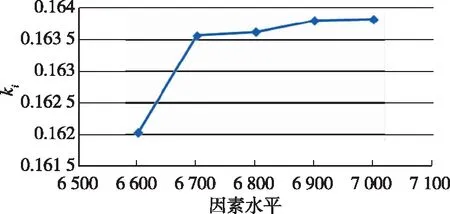
(a)L1
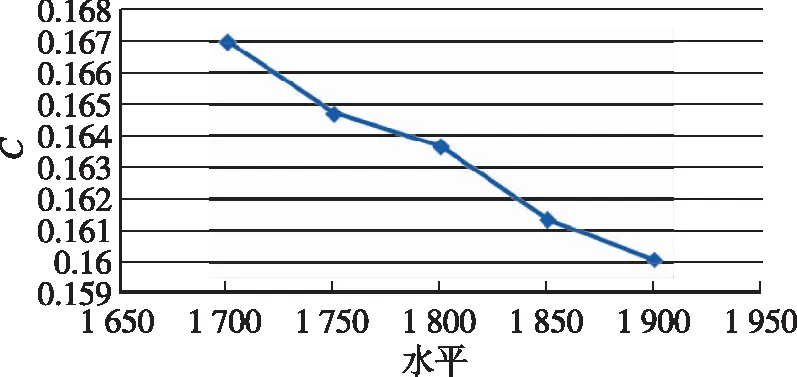
(b)D1

(c)L2
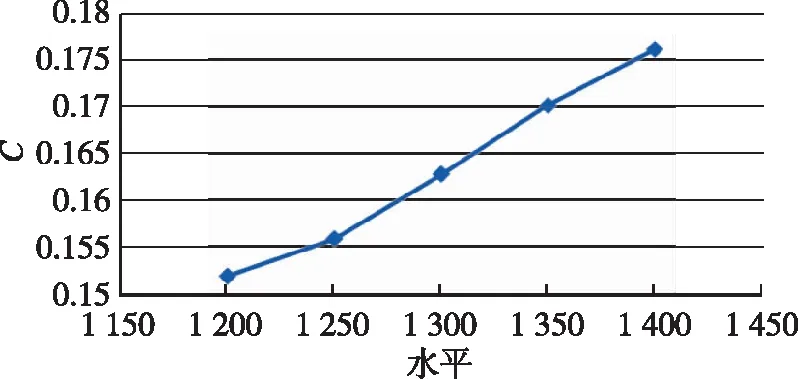
(d)D2
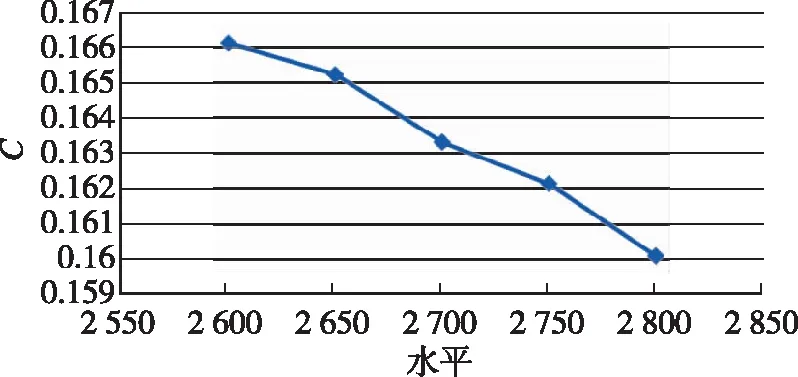
(e)L3图3 参数趋势图Fig.3 Trend of parameters
由图3(a)~(e)可知,对于飞行器外形,阻力系数对I级长度1和II级直径2逐渐增加,对I级直径和III级长度逐渐减小,对II级直径呈现出跳跃性波动。
4 结论
本文以飞行器气动外形设计分析为目标,利用正交试验设计方法,对阻力系数进行了试验。
1)试验结果表明,该方法能够快速对飞行器气动外形开展设计和分析,获得可行的设计方案,提高总体设计效率。
2)优方案可为飞行器气动外形精细优化提供可行的初始解,减少优化寻优次数。
