基于流固耦合航行体入水冲击数值模拟研究
2022-02-22于佳晖朱元夫
于佳晖,贾 亮,朱元夫
(北京强度环境研究所, 北京 100076)
0 引言
航行体入水过程引起周围流体介质的运动,流体介质对结构又施加反作用力,特别是在入水冲击初期瞬态间(毫秒级)过程中会遭受巨大的冲击载荷。结构入水冲击过程中形成的轴向力作用可能导致航行体头部变形、仪器设备失效等;法向力作用会出现忽扑和弹道失控等问题,并可能使结构弯曲破坏。
整个入水过程涉及航行体、水和空气三者之间的相互作用,同时在空泡生成过程中还涉及气液相变过程,具有强烈非线性、耦合性和非定常性。整个过程涉及两个主要问题: 一是航行体、自由液面、空泡之间相互作用的非定常流体力学问题;二是航行体高速撞水过程引起的结构力学问题。入水结构载荷分析及其稳定性研究在国内外仍是一大热点和难题,尚有许多理论、数值模拟以及试验等方面的难题需要解决。入水冲击问题较为复杂,通过理论分析解决此类问题较为困难。数值模拟和试验是研究高速入水问题的主要手段。 任意拉格朗日欧拉方法,解决了大变形和移动边界的流体耦合问题,该方法已被广泛用于入水问题的研究,并已集成在Dytran和LS-Dyna等软件中。2018年,Derakhanian等提出基于有限容积方法(FVM)、有限差分方法方法(FDM)和任意拉格朗日欧拉米德方法(ALE)进行数值模拟并分别与试验结果相比,结果表明ALE数值算法用于模拟这种流动固体相互作用问题具有可靠性且对于不同入射角度和入水速度计算冲击力更为准确。2011年,Luo等提出在结构和流体之间接触区域附近的网格尺寸对于仿真结果影响较大,但是对于远离接触区域的网格无明显影响。Howison等对小斜升角楔形体入水试验中存在压力振动现象进行分析,认为忽略气垫效应不会对计算结果产生很大差异。Wilson对入水冲击初始阶段交界面出现的气垫层进行建模,通过无量纲方法利用渐近理论得到解析解。Yettou等通过对5种楔形体模型以自由落体方式入水冲击进行试验,得出影响压力系数的重要因素,分析了各因素对冲击载荷变化的影响。
本文基于流固耦合ALE方法利用 LS-DYNA 软件数值进行航行体入水冲击问题数值模拟研究。用罚函数耦合计算方法求解入水冲击过程中流固耦合问题,分析网格密度、罚函数耦合系数以及时间步长等因素对数值仿真计算准确性的影响,形成入水过程三维数值建模方法。最后,建立航行体入水过程模型,研究不同速度对入水过程中加速度、速度以及位移的影响。
1 基于 ALE 的流固耦合方法
1.1 基本控制方程
基于任意拉格朗日欧拉算法的质量守恒方程和动量守恒方程如下
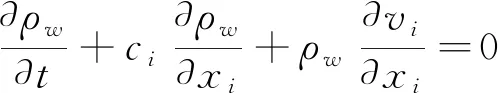
(1)
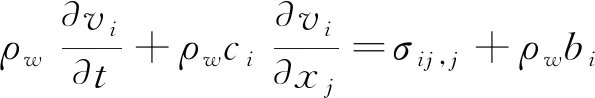
(2)
式中,为空间坐标;为描述下的对流速度,=-;为流体质点的物质速度;为网格速度;为流体密度;为流体体积力;为应力张量。
=-+(+)
(3)
式中,为水的静压,为动力黏性系数,为克罗内克函数。
1.2 流固耦合罚函数计算方法
ALE有限元方法研究三维入水冲击的水动力问题,使用欧拉方法离散流体,拉格朗日方法离散化结构,罚函数接触算法求解流体与固体之间的接触。固体结构与流体之间的界面由流体体积函数方法(VOF)获得。Luo等研究二维半球和锥体分析不同的入射角度和入水速度,通过与试验结果进行比较,发现冲击接触区域的网格密度对于结果准确性影响较大。
罚函数耦合的计算类似于弹簧系统,罚函数耦合力的计算与穿透深度和弹簧刚度成比例。弹簧的头部连接到结构从节点,尾部连接流体单元(结构穿透部分)主节点。与罚函数接触相同,耦合力表示为。
=
(4)
式中,表示弹簧刚度,表示穿透深度。耦合力在耦合处沿相反方向作用于主节点和从节点。
耦合问题中难点是对刚度的设置。基于LS-DYNA中的显式惩罚接触算法,刚度包含流体主单元与结构从单元关联部分单位面积的数值刚度体积模量,主节点流体单元体积以及连接到结构节点的结构单元的平均面积。
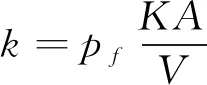
(5)
为了避免数值不稳定性,引入罚函数耦合系数以缩放相互作用(耦合)系统的刚度。对于冲击问题,罚函数耦合系数对解具有明显的影响。对于二维楔形入水问题,Luo等进行相关参数研究,包括罚函数耦合系数,时间步长因子,网格尺寸和联络点的数量,并通过将预测与Cui等实验结果进行比较来验证。结果表明网格尺寸对于模拟非常重要,而其他方面则影响很小。
2 数值仿真方法正确性研究
2.1 仿真模型
研究对象为球体以及带有圆锥头部柱体。为了验证ALE方法的准确性,首先建立球体模型不同入水速度垂直入水,并与De Backer等的试验进行比较。
在数值建模中结构的主要参数如表1所示,球体的直径为0.3 m,无表面张力效应。由于结构厚度大,在入水时不考虑弹性变形的影响。与试验对比首先设置较小的入水速度4 m/s。

表1 模型尺寸表
坐标轴如图1所示,为水平面,轴垂直于平面向上。结构入水角度为90°,垂直入水,入水速度为。
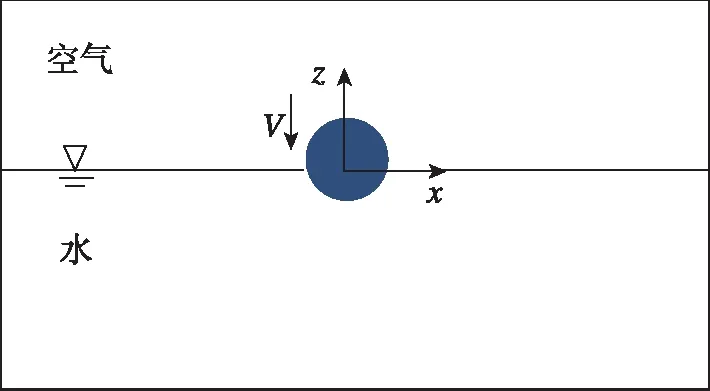
图1 球体垂直入水模型Fig.1 Computational model
流体(水和空气)定义为多材料区域,考虑水和空气多相流问题。流体域水和空气采用soild 11多材料单元,定义空气材料设置其状态方程。其中水域设置Gruneisen状态方程,空气域设置线性多项式状态方程。结构设置为soild1单元建模用于显式动态分析和刚体材料 。
施加罚函数接触耦合算法求解流体与结构之间的相互作用,通过定义流固耦合关键字*CONSTRAINED_ LAGRANGE_IN_SOLID。从单元选择拉格朗日实体单元; 主单元选择流体单元;耦合类型一般采用罚函数耦合方式; PFAC为接触刚度又称罚函数耦合系数。 罚函数接触耦合类似于弹簧系统,通过产生高振荡计算耦合力。
流域边界设置为对称边界,可扩大流域,减少液面升高现象。仿真流域长宽要求大于等于12倍的特征长度。设置计算域设置为5 m×5 m×8.5 m,其中空气域为5 m×5 m×1.5 m,水域为5 m×5 m×7 m。主要用于观察刚入水冲击载荷,以及入水后速度加速度变化规律。需要设置足够的流域,并进行边界无关性验证。
为了精确求解入水冲击问题,需要仔细选择网状密度和接触刚度。接触刚度与罚函数设置的罚函数耦合系数和流体单元体积所包含耦合节点有关,即流体的网格密度的影响。所以对于这两个影响因素做进一步的研究。
在仿真中记录表面压力随时间的变化,以及位移、速度和加速度。将仿真结果进行无量纲变换得到冲击系数与试验结果对比分析。
2.2 网格密度的影响
入水网格划分如图2所示,选择3种不同网状尺寸,分别为10 mm,5 mm和2.5 mm设置为接触区域流体网格大小。流体区域网格尺寸由结构物特征尺寸决定。分别为0067,0033和0016 7,其中表示球体的半径。结构尺寸设置为5倍的流体网格尺寸。
图2 球体入水网格划分图Fig.2 Water-entry simulation FEA mesh
无量纲冲击系数
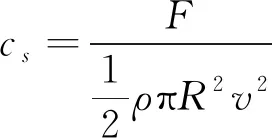
(6)
式中,为冲击力 ,为水密度100 kg/m,时间表示为=,其中是球体进入水面的时间,入水速度为4 m/s。
PFAC的值设定为0.1,得到接触刚度,接触刚度可由公式(5)估算,分别为22.5 GPa/m,45 GPa/m和90 GPa/m。如图3所示,当网格尺寸为0.016 7时,仿真结果除初始入水冲击阶段外与De Backer等的试验测量结果一致。在初始入水冲击阶段,冲击系数高于试验结果。因为在入水冲击初始阶段,流体和结构之间的相互作用仅为结构底部部分单元和水的表面单元。在初始冲击时,单元压力的数值脉冲是不可避免的,并且冲击力从沿着结构的湿表面的压力集合获得。当网格尺寸为0033和0067时,仿真结果与试验结果不一致。在入水冲击的后期,随着网格尺寸变大冲击最大值高于真实结果。另外,数值信噪比对与网格尺寸有关。可知,0016 7网格尺寸的仿真模型计算入水冲击力时间历程更准确。为验证数值结果的稳定性,进行不同入水速度的仿真计算。入水速度分别为4 m/s和18 m/s,入水冲击网格密度选择一致。

图3 不同网格密度球体的无量纲冲击系数结果Fig.3 Dimensionless impact coefficient of spheres with different mesh denisity
2.3 接触刚度的影响
引入罚函数耦合系数Pf(PFAC)以缩放耦合系统的刚度,需研究该参数对仿真模型结果的影响。基于网格尺寸的敏感性研究,选择具有0016 7网格的仿真模型,入水速度18 m/s,用于球体入水冲击仿真计算,仿真模型设置不同PFAC值分别为0.01,0.1和0.5。图4绘制着不同PFAC值冲击系数曲线,3条曲线在入水冲击的初始时刻有明显的区别,并且在峰值时刻一致,但总趋势相同。对于0.5 PFAC的模型,冲击入水结果信噪比低。

图4 不同接触刚度无量纲冲击系数结果Fig.4 Dimensionless impact coefficient of spheres with different contact stiffness
球体底部局部峰值压力对PFAC的值敏感。接触刚度越高,峰值越小。从压力时间历程结果中,得到球体接触平静的水面时,最大压力值产生。峰值对PFAC值敏感,主从节点上的耦合力通过接触刚度和穿透力之积计算得到,而接触刚度缩放值为PFAC的值。结构受到的冲击力对PFAC的变化不敏感,因为冲击力是结构的平均值。
3 数值仿真结果与分析
建立航行体入水冲击模型,结构柱体直径0.15 m、全长2 m、圆锥头部直径0.15 m,头部角度为60°,带锥体头部柱体垂直入水模型如图5所示。计算域设置为2 m×2 m×9 m,其中空气域为2 m×2 m×2 m,水域为2 m×2 m×7 m。流体区域网格尺寸设置为0.01 m,结构网格尺寸设置为0.015 m,并进行网格无关性验证。PFAC的默认值为0.1。仿真时间为0.04 s,主要分析刚入水阶段的加速度、速度和位移规律。

图5 带锥体头部柱体垂直入水模型Fig.5 Vertical water-entry model of cylinder with cone head
为研究航行体的截面载荷,必须要考虑航行体的弹性变形,但实际航行体结构复杂,完全建立航行体的弹性体模型会显著增加流固耦合计算时间。所以提出一种航行体入水冲击模型截面载荷计算方法,采用分段刚体的方法将结构简化,求出航行体在入水冲击过程中的截面载荷。将带锥形头部柱体用分段刚体进行离散,分段刚体之间用弹性梁进行连接。设置分段刚体为柱段中心截面处。
航行体入水时结构和空气垫及水的相互作用,使空泡区的水获得了较高的运动速度,而水介质不承受拉力易形成溅水。飞溅不属于连续介质力学范畴,用理论方法求解异常困难。但用仿真可模拟入水飞溅和超空泡效果,溅水效应和超空泡如图6所示。在入水各个阶段,水面压力如图7所示。当结构在水中超过一定速度时,空泡在结构周围形成并把结构包裹起来,直至形成超空泡,此时整个结构只有头部与水接触。

图6 锥头柱体垂直入水不同时刻状态图Fig.6 Different times of vertical water-entry
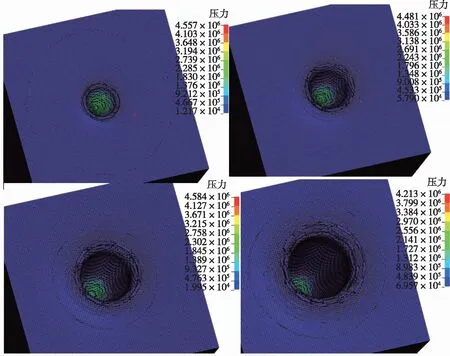
图7 锥头柱体垂直入水不同时刻状态水面压力图Fig.7 Water surface pressure at different times
图8为锥体头部以入水速度120 m/s垂直入水,接触水之后的0.04 s期间加速度、速度和位移结果,并与试验结果进行对比。LS-DYNA仿真具有较高准确性,速度误差在10%以内。LS-DYNA获得的冲击速度低于试验中测量的冲击速度,随着时间的推移,它们之间的差异变大,速度误差产生的原因是仿真模型结构自由运动产生的摩擦大于测试系统实际摩擦。位移即入水深度在0.04 s内误差较小,但随着时间的推移,测量值和仿真模型的偏差逐渐加大。垂直入水工况下的截面弯矩数值较小,截面弯矩产生阶段为入水冲击阶段以及空泡闭合阶段。在高速入水工况下,入水瞬间以及空泡闭合时的尾拍都会使航行体受到明显的弯矩载荷。
垂直入水工况改变入水初速度,通过对仿真结果分析可得到随着入水初速度的衰减,加速度幅值变化如图9所示。随速度增加,加速度幅值开始变化较小,随后变化明显。这可能是因为超空泡显著降低了结构在入水初始阶段的阻力。随着初始速度的增加,结构在入水冲击瞬间受到的截面弯矩载荷逐渐增大,轴向冲击载荷的峰值呈上升趋势。
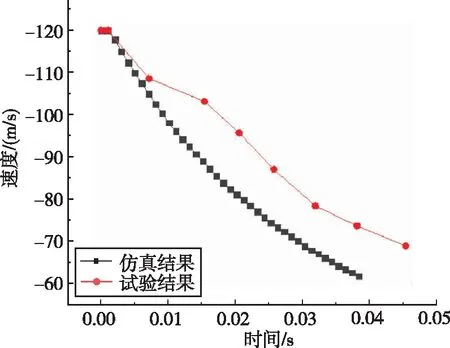
(a) 速度随入水时间结果
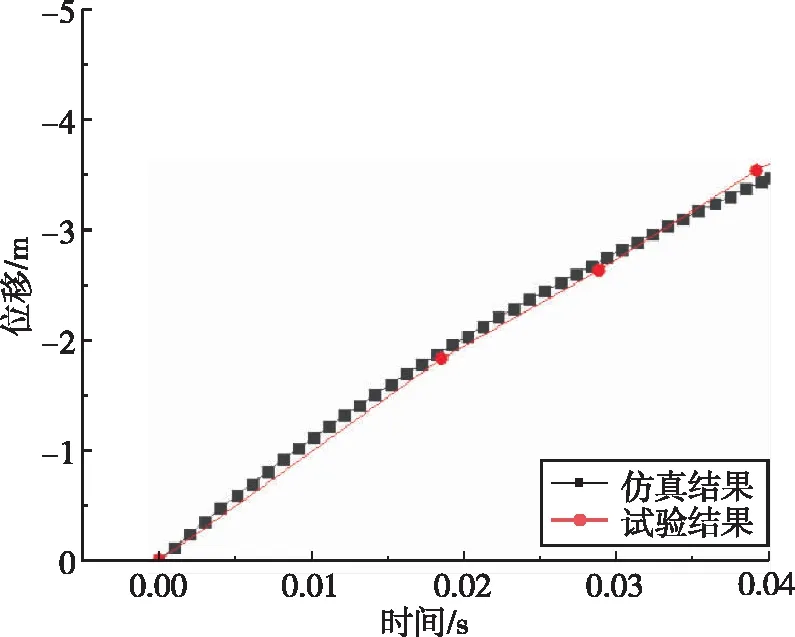
(b) 位移随入水时间结果
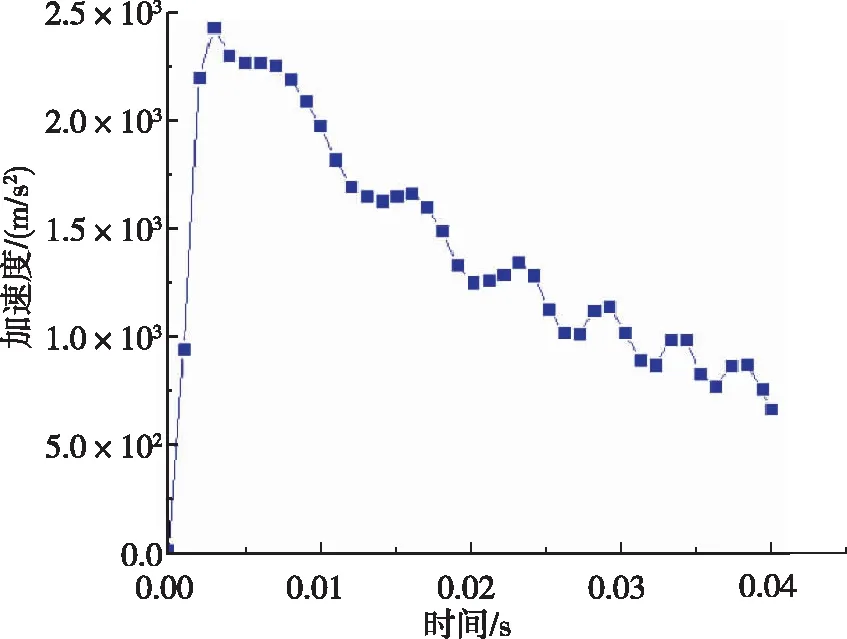
(c) 加速度随入水时间结果
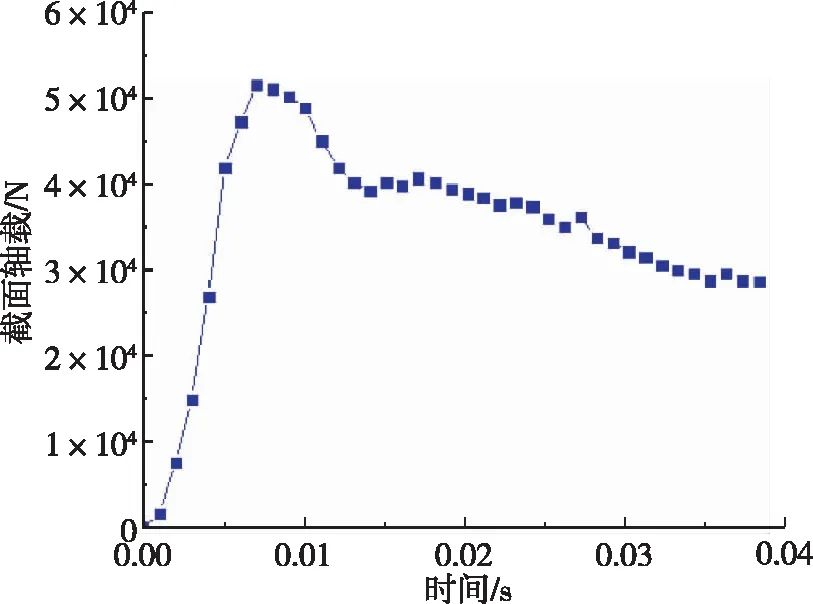
(d) 截面轴载随入水时间结果
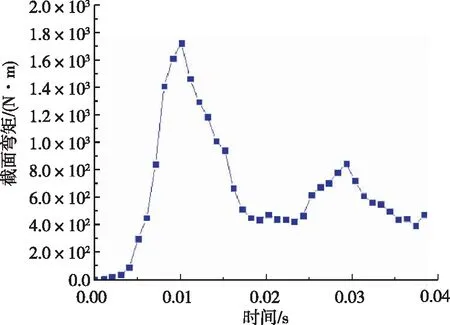
(e) 截面弯矩随入水时间结果图8 锥头柱体120 m/s垂直入水加速度、速度、位移和截面载荷结果Fig.8 120 m/s vertical water-entry acceleration, velocity and displacement
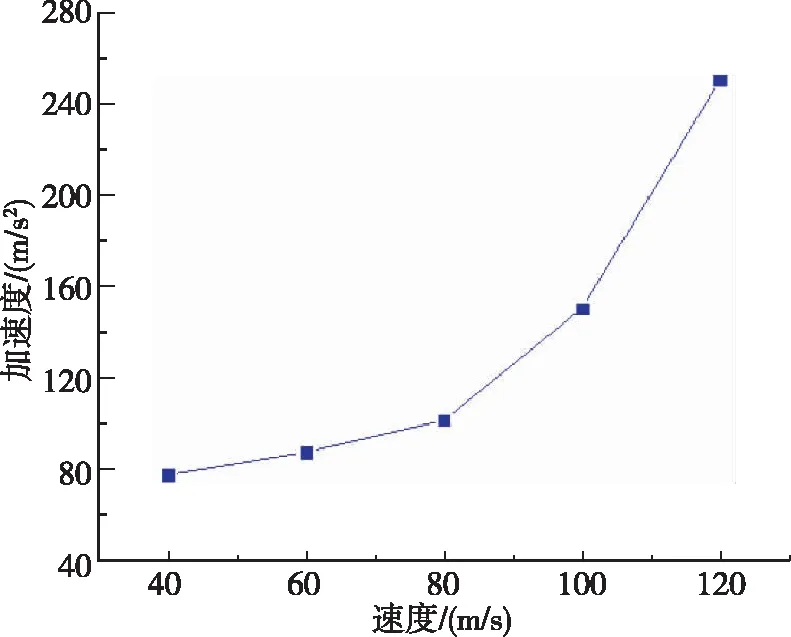
(a) 不同速度对入水瞬间最大加速度的影响
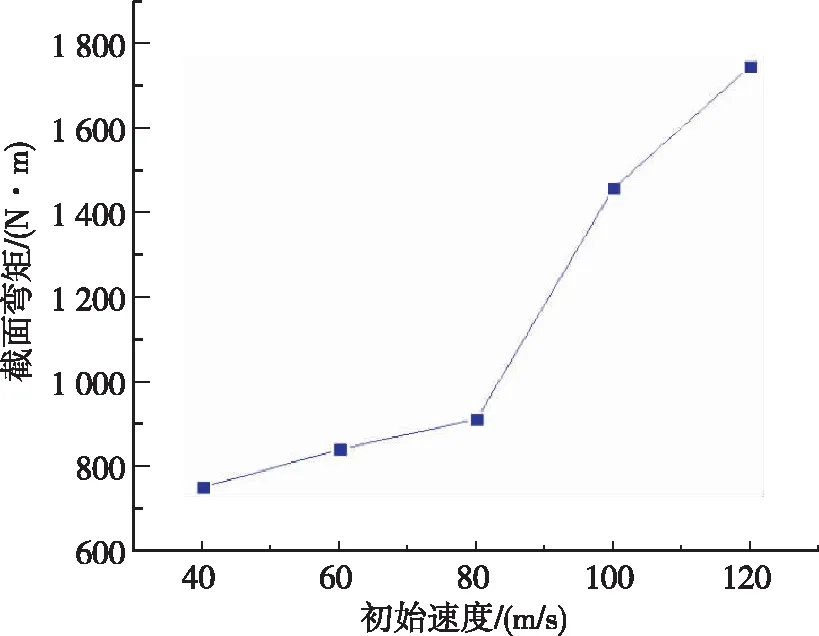
(b)不同速度对入水瞬间最大截面弯矩的影响图9 不同入水初速度下加速度、截面弯矩峰值结果Fig.9 Acceleration and section bending moment under different initial water-entry velocities
4 结论
1) 基于流固耦合运用ALE 算法研究三维航行体入水冲击数值模拟方法,获取了模型入水冲击过程中的冲击系数、表面压力、加速度、速度及流固耦合形态等结果。
2)对比试验分析网格密度、接触刚度以及时间步长对数值仿真模型准确性的影响。冲击区域网格密度和接触刚度耦合系数决定流固耦合接触刚度。网格密度对数值模型准确性非常重要,尤其是对于冲击系数以及加速度的准确预估。耦合因子PFAC对于结构所受表面压力具有一定的影响,但结构上受力对耦合因子不敏感。
3)针对锥形头圆柱体模型垂直入水,建立不同入水初速度下的仿真模型,提出分段刚体计算截面载荷方法,研究不同速度下结构入水冲击加速度、速度、位移和截面载荷变化规律。结果表明,入水冲击模型准确度高,验证了仿真方法的有效性。入水速度越大,结构振动和冲击最大幅值越高。随着初始速度的增加,结构在入水冲击瞬间受到的轴向冲击载荷和截面弯矩载荷逐渐增大。
