唤醒与鼓舞下的说理课堂

范林伟

第斯多惠曾说：“教学的艺术不在于传授本领，而在于激励、唤醒和鼓舞。”罗鸣亮老师积极倡导说理课堂，擅于为学生提供说理的表达时间与话题空间，使学生在交流、质疑与补充中构建新知，不断体验对话的智慧，充分感受成功的自信与满足。本文结合五年级“分数与除法”一课，谈一谈罗老师“以退为进”的教学艺术。

一、问题引入，暴露学习困难

课始，罗老师依次报出五道除法算式“6÷3、72÷9、2÷3、3÷8和11÷17”，让学生将算式与结果记录下来。

师：你们都算好了吗？遇到什么困难？谁愿意把自己的困难大胆地说出来？

生₁：除不尽。

生₂：我们以前的除法算式，被除数比除数大。今天的是被除数比除数小，没法除。

生₃：算出来的结果不是整数。

【賞析】数学教学应关注学生的旧知，引导学生在原有学习经验的基础上进行学习。看似简单的几个算式，却巧妙地连接着旧知与新知。6÷3和72÷9两个算式有利于唤醒学生口算除法的经验，使其回忆起除法算式的结果一般为整数。2÷3这个算式既便于学生利用竖式计算得到小数的计算结果，又利于唤醒学生借助分数的意义来尝试解决问题的经验。其他几个算式则明显地使学生体会“商不是整数”的现象，从而暴露学生的真实困难，为课堂的推进埋下伏笔。

二、独立思考，激发学生思维

师：不着急，我们先从2÷3开始，它的商是几呢？（等待）我已经为大家准备了学习单，把你的想法写一写。

学生组内交流，再展示反馈。

生₄：如果像这样（竖式）除下去，会得到0.666……数字6会不断重复，可以用循环小数表示。

生₅：我用分数来表示。分数很神奇，我们可以把分数线看作除号，如1/4就是1÷4的商，分数线上面的就是被除数，分数线下面的就是除数。所以，2÷3=2/3。

师：你怎么知道的？

生₅：我妈妈教我的。

师：这位同学告诉我们，他妈妈告诉他等于2/3，但是他说不出为什么等于2/3。这是什么道理呢？请大家继续独立思考。

学生画图再探究，分析其算理。

师：他妈妈告诉他2÷3=2/3，对不对呢？把你的想法先在四人小组进行交流。

学生讨论，交流成果。

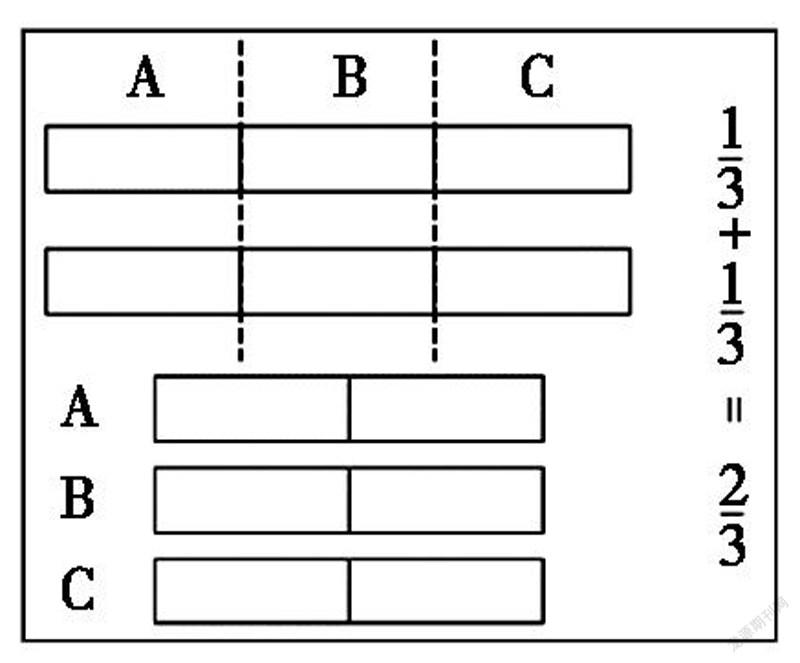
生₆：刚才我是结合了生活中的例子来说明的。比如，2块饼平均分给3个人。首先，把这块饼平均分成3份，这份给A、这份给B、这份给C。这样的一份就是1/3，每个人分到2个1/3，合起来就是2/3。（如左图）

师：他说的有没有听懂？或者谁还有不同的想法？

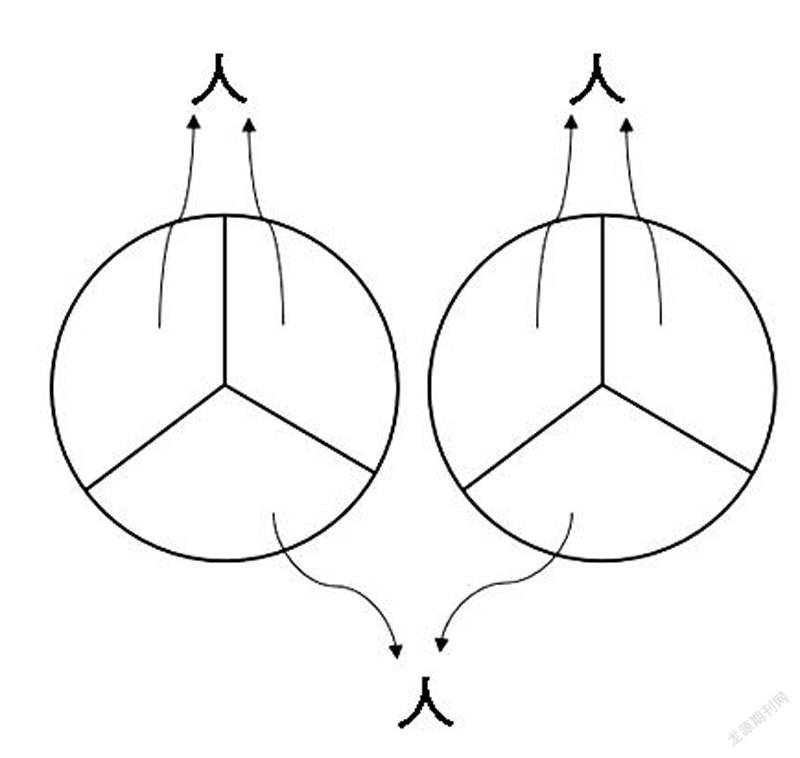
生₇：他是用饼来做例子，我是用这个圆来表示蛋糕。每块蛋糕一共有3份，那每个人就能拿到这块蛋糕中的两份。这个人可以拿到两份，这个人也可以拿到两份，这个人也可以拿到两份，所以答案是2/3。（如左图）

【赏析】本环节中，学生虽然“知道”结果，但罗老师并未急于将道理一语道破，而是组织学生先画一画，再交流分享。其间，教师将探究的主动权、发言的互动权交给学生，以核心问题“这是什么道理呢”引导学生在有目的、有方向的活动中探寻分数作为商的定义背后的原理。

三、深度体验，自主建构新知

师：现在这个问号可以擦掉了吗？2÷3知道了，那3÷8你们有没有办法去研究？看谁能说出道理，开始吧！

小组交流，全班反馈。

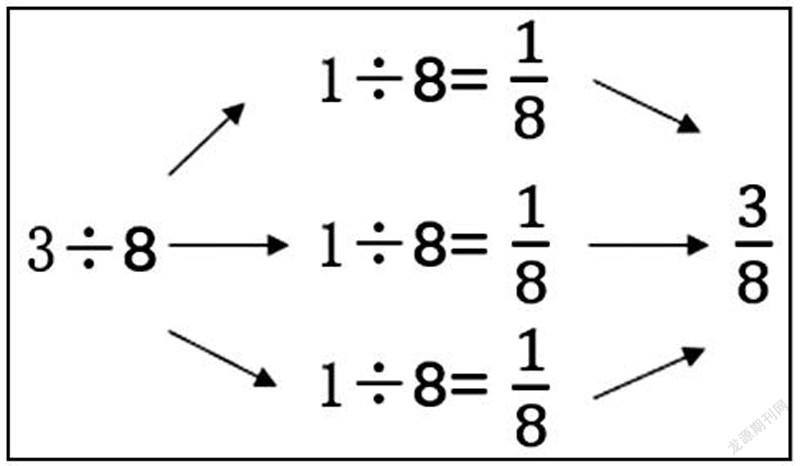
生₈：比如，有3块饼，第1块饼平均分成8份，那么1个人只能吃到1份。所以，第1块饼，每个人吃到的是1/8；第2块饼，每个人吃到的也只是1/8；第3块饼，也是同样的1/8。所以，3块饼加起来是3/8，每个人吃到3÷8=3/8。大家有什么疑问或补充吗？

生₉：我觉得还可以把3块饼全部叠起来，把3块饼平均分成8份，然后每人得到1份，所以用1/8加1/8加1/8等于3/8。

师：不管像他一样，一块一块地分，每人拿到1个1/8、2个1/8、3个1/8；还是像那个同学一样，把3块饼叠起来分，都是拿到几个1/8？

生₁₀：3个1/8。

师：虽然他们的分法不同，但是都得到3个1/8，因此3÷8等于多少？

生₁₁：3/8。

师：我们起先还有一道算式，那11÷17又等于多少呢？有想法的请举手。不过，我们不仅要知道结果，更要能讲清楚为什么，把你的想法小声地和同桌说一下。

师追问：我们要感谢你，你特别棒！你能把妈妈告诉你的2/3的结果分享给大家，我更希望你能把11÷17=11/17的道理说给大家听，你会说吗？

生₅：可以！比如，我们这里有17个人，这里有11桶水，请大家想象一下——每个人有一个大杯子，每一桶分出1/17给每一个人，第2桶同样操作，一直到第11桶水也是这样操作。那么，我们就有11个1/17，就是11/17。

师：我们从开始解决3个算式时出现了困难，到现在知道了其中的道理。那么，现在你能不能自己举个例子，然后想一想答案背后的道理，再来考一考你的同桌呢？

学生自由交流，写算式并向同桌解释说明。

师：其实我最好奇的是，你们到底都举了什么例子来考你的同桌？

生₁₂：我举的算式是9÷19=9/19。

师：你的同桌呢？

生₁₂：他举的算式是999÷1011=999/1011。

生₁₃：一共有1011个人，要分999张饼。第1张，第1次能分到1/1011张饼，然后第2次也是这样，一共分到999块这样的饼，结果就是999个1/1011，就是999/1011。

【赏析】在学生成功解决2÷3之后，罗老师以3÷8和11÷17再次引领学生进行探究，使学生在“画一画、说一说、考一考”的活动中进行深度体验，全面建构新知。同时，罗老师多次用鼓励的语言，促使学生大胆展示自己的观点，激发他们的表达欲望。

四、适时介入，拓宽数学思考

师：如果是我，我会考我的同桌什么，想知道吗？我会问4÷3=？不着急，把你的答案写在学习单的背面。

学生书写，再次探究并小组交流。

生₁₄：你们看，就是一块饼先平均分成3份，然后一份给A、一份给B、一份给C。然后，第2块饼、第3块饼、第4块饼也是这么分。所以，每一个人都是1/3+1/3+1/3+1/3等于4/3块饼。当然，还有一个方法是，这块饼全部给A，这块饼全部给B……最后这块饼平均分成3份，这一份给A、这一份给B……加起来也正好是4个1/3，就是4/3。你们还有问题或补充吗？

生₁₅：第1块饼全部给A，第2块饼全部给B……然后第4块饼平均分成3份，这一份给A，这一份给B……就是每人有1块了，再加1/3，就是11/3。

师：很好！特别棒，他们表达了两种不同的分法，也就是4÷3=4/3=1  1/3，而且你们还知道1  1/3是什么分数？

生齐：带分数。

【赏析】学生是学习的主体，教师是课堂的主导。教学中，罗老师该出手时就出手，以“我会考我的同桌什么”再次将课堂探究推向高潮，以挑战性任务“4÷3=？”驱动学生进行再创造。于是，学生根据课堂学习经验与广泛的认知，成功地解决问题，深化了对算理的理解。这便让学生理解了无论被除数或除数哪个大，都可以用分数来表示商。

五、回顾反思，总结学习经验

师：聪明的孩子们，观察一下我们一开始遇到的困难，还有我们举的这些例子，你有什么发现吗？悄悄地把你的发现说给同桌听一听。

同桌交流，表达观点。

生₁₆：我们发现，如果是小的数除以大的数，它就是可以用小的数来做分子，大的数作分母。如果是大的数除以小的数，那么就是被除数作分子，除数作为分母。

生₁₇：大数除以小的数也可以先用二年级学过的除法得出商，然后得出它的余数，再用余数去除以除数，把刚才得出来的商，与余数除以除数的商加起来。

生₁₈：我发现上面一行的分子都比分母要小，是真分数；下面一行，分子都比分母大，是假分数。

师：如果被除数为a，除数为b，当然b不等于0。那么，想一想a除以b就可以等于多少？

生₁₉：a/b。

师：回忆一下这节课，你有收获吗？不着急，把你的收獲跟同桌说一下。

【赏析】课尾，罗老师带着学生重新回顾本节课的收获。与日常不同的是，他是先引导学生悄悄地把自己的发现说给同桌听，再提炼分数与除法的关系。如此，学生的学习感悟会更加深刻，学习成就感也会更加浓厚。

郭思乐教授指出，学生是教育对象更是教育资源。整节课，罗老师虽然隐藏在学生背后，却时刻关注着课堂生成，以退为进组织课堂活动，使课堂上充满学生的操作与展示、质疑与补充。教师的“退”成就了学生的“进”，教师所展现的“不着急”“谁能说出道理”等朴素的语言给予了学生巨大的精神动力，使他们不畏困难，勇于探索，精益求精地完善自己的数学思考。

（作者单位：浙江师范大学附属嘉善实验学校

责任编辑：王彬）