银行理财产品刚性兑付协同治理研究

卿文芳 黄大富 李善民

（中国人民银行百色市中心支行，广西 百色 533000）

一、引言

我国银行理财产品市场起步于2004年，近十几年间银行理财产品发行规模保持年均100%左右的增长，经历从无到有、由小到大的快速发展过程。银行理财产品作为我国新兴的财富管理工具，其募集的市场规模超过券商集合理财产品和证券投资基金，已成为我国资产管理市场上重要的组成部分。在银行理财产品快速发展的同时，其弊端也日益凸显，主要表现为银行理财产品刚性兑付所引发的风险集聚。从理论上说，银行理财产品的原则应该是卖者尽责，买者自担风险、自负盈亏。但在实际运行中，银行都是按照理财产品的预期收益率进行刚性兑付。近年来，愈演愈烈的刚性兑付危机问题引起社会各界的广泛关注和热烈讨论。各界普遍认为银行理财产品刚性兑付，一方面维护金融消费者权益和银行声誉，推动银行理财业的快速发展（王一鸣和王立夫，2022；王剑锋等，2020）；但另一方面，也提高金融市场的无风险收益率、推高社会融资成本、扭曲金融资产的风险与收益有效配置。打破银行理财产品刚性兑付，让理财产品回归“卖者尽责、买者自负”的本源，成为社会各界的广泛共识（孙希芳和刘立彧，2022；马天平，2019）。

由此，如何构建良性治理机制，以便有效打破银行理财产品刚性兑付，成为亟待解决的问题，有必要对银行理财产品刚性兑付的形成原因进行梳理。归纳起来主要有两个方面：一是银行声誉。一方面，银行理财产品刚性兑付有助于降低信息不对称导致的成本，增加了公众对银行理财的信任度和理财收益预期，展示了银行理财的良好形象和经营能力，扩大了银行资管规模和资金来源渠道，为银行提供更为灵活便利的流动性管理手段（王占浩等，2020；周乾，2021）。另一方面，如果银行在理财产品到期时未按照约定收益率进行兑付，那么可能会引发银行的声誉风险，进而拖累银行理财业务发展（崔明，2015）。二是扶植保护。银行理财业务在我国起步较晚，金融法规和市场监管滞后，银行理财推行刚性兑付能够增强投资人信心，有利于银行拓展资产管理业务，保障投资人权益，并能够补齐消费者权益空缺。针对如何构建一个良性机制打破银行理财产品刚性兑付问题。学者们多从两个方面提出治理对策。一方面是修改完善相关法律法规。针对现有的《中华人民共和国信托法》，部分学者主张对其进行修改和完善，比如对受托人谨慎义务的标准与内容进行细化和明确（周乾，2016）。另一方面是明确监管机构职责，对委托人和受托人两个方面加强管理，真正做到“卖者尽责，买者自负”，有些学者提出由金融监管部门牵头建立统一的投资者适当性管理体系标准，有效落实现代金融交易的诚信原则与契约精神（杨峻，2017）。

纵观目前的研究，现有文献对银行理财产品刚性兑付治理的分析视角较为宏观，缺乏对打破银行理财产品刚性兑付微观机制研究。与既有研究相比，本文可能的贡献如下：一是研究视角新颖，本文从协同治理视角将演化博弈理论应用于银行理财产品刚性兑付问题研究，将金融监管部门与银行业金融机构结合起来，构建一个完整的银行理财产品协同治理的演化博弈，为金融监管部门和银行协同治理银行理财产品刚性兑付提供了理论依据和作用路径。二是本文的研究为监管部门和银行业金融机构参与化解资管业务刚性兑付困局提供良好参考和有益启示。

二、银行理财产品刚性兑付协同治理的演化博弈模型构建

从现实情况看，银行理财业务易受金融监管部门和金融监管政策的影响，银行的经营行为和经营模式随着金融监管政策和监管行为的变化而不断调整。演化博弈理论能够较好地刻画银行理财市场博弈主体策略选择的动态变化（李善民，2019；Friedman，1991）。有鉴于此，下文运用演化博弈理论对银行理财产品刚性兑付的协同治理进行研究。

（一）金融监管部门参与监督的情形

考虑到参与银行理财市场的银行较多，为方便分析，假设参与博弈的银行仅为银行1和银行2。当金融监管部门参与银行理财产品刚性兑付协同治理时，博弈参与人变为银行1、银行2和金融监管部门三方，银行1和银行2有采取协同治理（非刚性兑付）和非协同治理（刚性兑付）两种策略选择。同样，金融监管部门也有采取监督和不监督两种策略选择。由此，对四种情形进行分析。

情形一：假设银行1与银行2都采取非协同治理时，双方各自收益分别为ψ1和ψ2，由于金融监管部门参与监管，金融监管部门给予银行1和银行2的罚款分别为λ1和λ2，在下文中λ1和λ2也是监管部门的监管收益，此时银行1的收益变为ψ1-λ1。银行2的收益变为ψ2-λ2。

情形二：当银行1和银行2均采取协同治理策略时，此时整个银行理财市场会产生Δψ的协同收益。但考虑到银行理财市场的银行较多，银行1和银行2采取协同治理策略后会使银行1和银行2的理财市场份额流失，因此产生c1和c2的额外成本。同时由于银行规模和经营模式的差异，协同增量对银行1和银行2的分配可能存在差异，为此进一步假定，银行1获得的协同收益增量比例为p，银行2获得的协同收益增量比例为1-p。最终银行1的收益为ψ1+pΔψ-c1，银行2的收益为ψ2+(1-p)Δψ-c2。

情形三：当银行1采取协同治理策略，而银行2采取非协同治理策略时，银行1因市场份额流失而造成额外损失c1，但银行1会得到金融监管部门给予的激励r1；银行2会得到因银行1协同治理产生的额外收益Δv2以及监管部门的罚款λ2。最终银行1的收益为ψ1-c1+r1，银行2的收益为ψ2+Δv2-λ2。

情形四：当银行1采取非协同治理策略，而银行2采取协同治理策略时，银行2因市场份额流失而造成额外损失c2，但银行2也会得到金融监管部门的激励r2，银行1会得到因银行2协同治理而产生的额外收益Δv1以及金融监管部门的罚款λ1。则银行1的收益为ψ1+Δv1-λ1，银行2的收益为ψ2-c2+r2。

为方便分析，假设金融监管部门的基准收益为ψ3，金融监管部门监管成本为c3。金融监管部门参与银行协同治理博弈的收益矩阵如表1所示。

表1 金融监管部门参与银行协同治理的三方收益矩阵

（二）金融监管部门不参与监督的情形

金融监管部门不参与监督，假设银行1与银行2都采取非协同治理时，不会受到金融监管部门惩罚，此时双方各自收益分别为ψ1和ψ2。当成员银行双方都采取协同治理策略时，会产生Δψ的协同收益。同样地，对于协同收益增量的分配，银行1获得的比例为p，银行2获得的比例为1-p，则银行1的收益为ψ1+pΔψ-c1，银行 2的收益为ψ2+(1-p)Δψ-c2。当银行1采取协同治理策略，而银行2采取非协同治理策略时，银行1虽然会因失去部分市场份额造成额外损失c1，但可以获得金融监管部门激励r1；银行2会获得因银行1协同治理产生的额外收益Δv2，则银行1的收益为ψ1-c1+r1，银行2的收益为ψ2+Δv2。当银行1采取非协同治理策略，而银行2采取协同治理策略时，银行2会因市场份额减少而造成额外损失c2，但会获得金融监管部门激励r2，银行1会得到因银行2协同治理产生的额外收益Δv1，则银行1的收益为ψ1+Δv1，银行2的收益为ψ2-c2+r2。

进一步假定，金融监管部门的基准收益为ψ3。金融监管部门不参与银行协同治理博弈的收益矩阵如表2所示。

表2 金融监管部门不参与银行协同治理的三方收益矩阵

假设银行1采取协同治理策略的概率为x，银行1采取非协同治理策略的概率为1-x。银行2采取协同治理策略的概率为y，银行2采取非协同治理策略的概率为1-y。金融监管部门采取监督策略的概率为z，金融监管部门采取不监督策略的概率为1-z。

通过对银行1、银行2和金融监管部门的假设，本文构建出三方演化博弈的决策树，如图1所示。

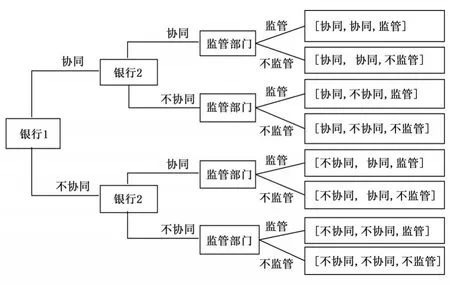
图1 三方演化博弈过程的决策树

三、银行理财产品刚性兑付协同治理的三方演化博弈均衡分析

（一）银行1的复制动态方程及其演化稳定策略

（二）银行2的复制动态方程及其演化稳定策略

（三）金融监管部门的复制动态方程及其演化稳定策略

在分别讨论各自的复制动态过程及均衡状态后，进一步分析三个群体组合形成系统的博弈均衡状态。首先结合式（2）、式（5）以及式（8）得到银行1、银行2和金融监管部门选择策略的三维动力系统（I）：

由Fx(x,y,z)、Fy(x,y,z)和Fz(x,y,z)可得：

对于系统（I），当x=0或1、y=0或1以及z=0或1时，恒有Fx(x,y,z)=0、Fy(x,y,z)=0和Fz(x,y,z)=0，因 此 ，(0,0,0)、(0,0,1)、(0,1,0)、(0,1,1)、(1,0,0)、(1,0,1)、(1,1,0)、(1,1,1)是系统（I）的均衡点。

四、银行理财产品刚性兑付协同治理的三方演化博弈稳定性分析

为了判断8个纯策略均衡点的稳定性，先由点(0,0,0)、(0,0,1)、(0,1,0)、(0,1,1)、(1,0,0)、(1,0,1)、(1,1,0)、(1,1,1)计算出dFx/dx、dFx/dy、dFx/dz、dFy/dx、dFy/dy、dFy/dz、dFz/dx、dFz/dy以及dFz/dz的具体取值，具体如表3至表5所示。

表3 局部均衡点在dFx下的不同取值

表4 局部均衡点在dFy下的不同取值

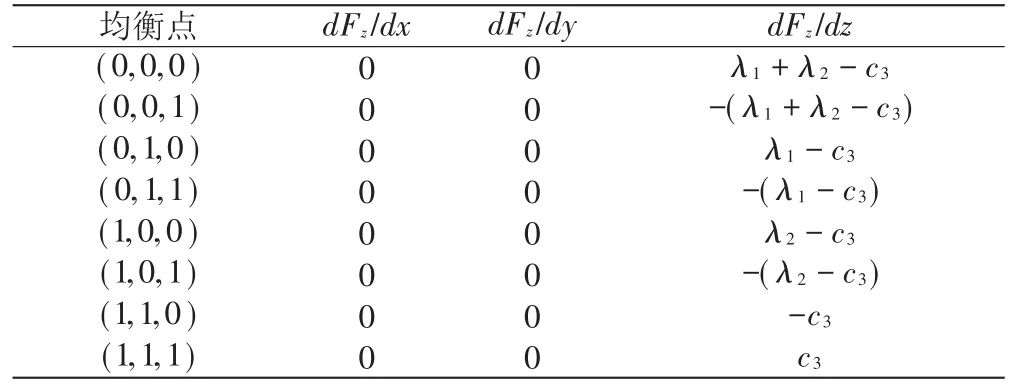
表5 局部均衡点在dFz下的不同取值

结合表3至表5可知，当满足一定的弱条件时，可以实现 8 个纯策略均衡点(0,0,0)、(0,0,1)、(0,1,0)、(0,1,1)、(1,0,0)、(1,0,1)、(1,1,0)、(1,1,1)的演化稳定性。考虑到银行1、银行2和金融监管部门参与银行理财产品刚性兑付协同治理是本文分析重点，所以这里重点对(1,1,1)的演化稳定性进行分析，具体如表6所示。

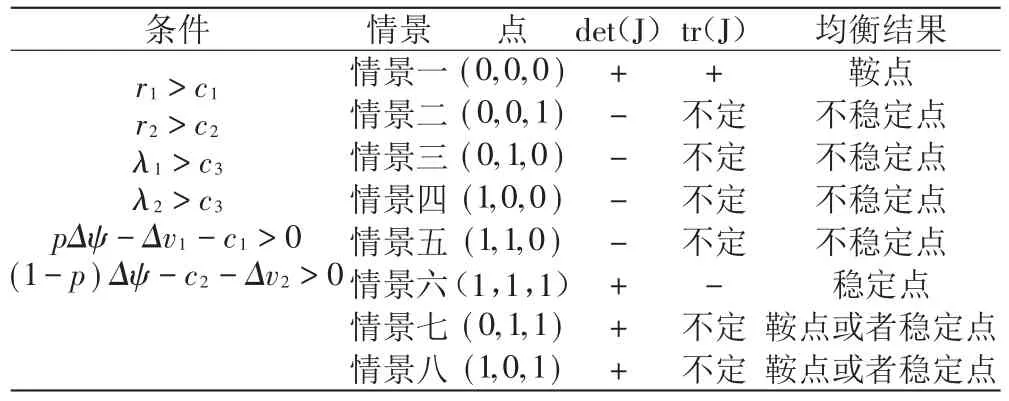
表6 8种情景下系统平衡点的稳定性判断结果

由表6可知，当r1＞c1，r2＞c2，λ1＞c3，λ2＞c3，pΔψ-Δv1-c1＞0以及(1-p)Δψ-c2-Δv2＞0成立时，系统（I）的均衡点(0,0,0)是鞍点，均衡点(0,0,1)、(0,1,0)、(1,0,0)以及(1,1,0)是不稳定点，均衡点（1，1，1）是演化稳定点；而均衡点(1,0,1)和(0,1,1)有可能是鞍点，也有可能是演化稳定点。

在上述8个均衡点中，均衡点（1，1，1）是系统可以明确显示的演化稳定点，对应于银行1、银行2以及金融监管部门采取“协同治理，协同治理，监管”策略。而均衡点(1,0,1)和(0,1,1)有可能是鞍点，也有可能是演化稳定点，这说明从长期演化过程看，系统可以实现均衡点从(1,0,1)和(0,1,1)向（1，1，1）演化。所以，在相同条件下，金融监管部门参与银行间的协同治理更有利于实现系统的演化稳定策略，帮助银行更好地进行协同治理。

五、银行理财产品刚性兑付协同治理的演化路径

前文分析可知，只有满足r1＞c1，r2＞c2，λ1＞c3，λ2＞c3，pΔψ-Δv1-c1＞ 0以及(1-p)Δψ-c2-Δv2＞0时，才能实现银行理财产品刚性兑付协同治理下各博弈主体演化系统的最终收敛结果。所以通过金融监管部门参与，有利于对协同要素进行控制，可以在不改变相关条件的基础上对初始状态参数进行调整，提高银行1与银行2采取协同治理的概率，从而使演化博弈模型中的各要素在支配作用下实现协同效应。

从前文的博弈分析过程可以看出，三个可控的初始状态参数在三方博弈中起到关键性作用：一是金融监管部门的监管成本c3；二是金融监管部门给予的罚款λ1和λ2；三是金融监管部门的激励r1和r2。这三个可控初始状态参数决定了银行理财产品刚性兑付治理中协同域与非协同域的大小，直接影响到博弈主体的策略选择及系统的稳定策略均衡。接下来，本文重点对金融监管部门的监管成本c3、金融监管部门额外罚款λ1和λ2以及金融监管部门给予的额外激励r1和r2进行分析，以促使三方博弈系统向所需的稳定点演化，进而实现三方协同效应。

（一）金融监管部门的监管成本c3

三方演化博弈系统中，监管成本c3表示金融监管部门对银行1和银行2参与银行理财产品刚性兑付协同治理监管时所产生的监管成本。根据前文分析可知，随着监管成本c3的增大，系统演化至（1，1，1）的概率会减少，而演化至（0，0，0）的概率增加。具体而言，当金融监管部门的监管成本c3满足c3＞λ1+λ2+r1+r2-(c1+c2)时，均衡点(0,0,0)的雅可比矩阵J行列式detJ大于零，其迹trJ小于零，此时均衡点(0,0,0)是三维动力系统（I）的稳定点。反之，随着监管成本c3的下降，三方演化的均衡点将逐渐向（1，1，1）演化，系统演化至（1，1，1）的概率也会增加，而演化至（0，0，0）的概率减少。

（二）金融监管部门给予的激励r1和r2

三方演化博弈系统中，激励r1和r2表示金融监管部门对银行1和银行2采取协同治理策略的额外激励。根据前文分析可知，随着激励r1和r2的减小，系统演化至（1，1，1）的概率会减少，而演化至（0，0，0）的概率增加。具体而言，当金融监管部门给予银行1和银行2的激励r1和r2满足r1+r2＜c1+c2+c3-(λ1+λ2)时，均衡点(0,0,0)的雅可比矩阵J行列式detJ大于零，其迹trJ小于零，此时均衡点(0,0,0)是三维动力系统（I）的稳定点。反之，随着金融监管部门对银行1和银行2参与理财市场刚性兑付激励r1和r2的增大，三方演化的均衡点将逐渐向（1，1，1）演化，系统演化至（1，1，1）的概率也会增加，而演化至（0，0，0）的概率减少。

（三）金融监管部门给予罚款λ1和λ2

三方演化博弈系统中，罚款λ1和λ2表示银行1和银行2采取非协同治理策略时，金融监管部门给予的罚款。根据前文分析可知，在金融监管部门采取监督的情形下，随着罚款λ1和λ2的减小，系统演化至（1，1，1）的概率会减少，而演化至（0，0，0）的概率增加。反之，要使点（1，1，1）演化为稳定点，只需要增大罚款λ1和λ2，随着罚款λ1和λ2的增大，三方演化的均衡点将逐渐向（1，1，1）演化，系统演化至（1，1，1）的概率增加，而演化至（0，0，0）的概率减少。具体而言，当金融监管部门给予银行1和银行2的罚款满足λ1+λ2＞c3成立时，均衡点(0,0,0)的雅可比矩阵J的迹trJ大于零，行列式detJ小于零，此时均衡点(1,1,1)是三维动力系统（I）的稳定点。

六、仿真模拟

为更加直观描述银行理财产品刚性兑付协同治理的演化路径，本文运用仿真模拟技术对金融监管部门与银行业金融机构构成的一个真实系统进行计算机模拟。为此，在满足三方演化稳定策略的条件下对参数进行如下赋值：p=0.6，c3=6，r2=15，c2=7，λ1=25，λ2=18，△ψ=42，△ν1=5，△ν2=7，c1=8，r1=10。其中，令x0、y0、z0依次为银行1采取协同治理策略、银行2采取协同治理策略以及金融监管部门采取监督策略的初始概率。x0∈{0.2,0.3,0.4, 0 .9}，y0∈{0.2, 0 .5 }，z0∈{0.3, 0 .4}。

（一）博弈主体策略选择初始概率对演化博弈系统的影响

为了模拟真实情况，设定x0、y0、z0分别取0.2、0.2和0.3，代表参与主体初始条件的不同情形。图2显示了银行1、银行2与金融监管部门之间的演化博弈均衡彼此影响、相互作用。三个群体一直处于周期性波动之中，无法统一趋于某一均衡状态，这表明博弈系统均衡不仅跟博弈主体自身策略选择的初始概率有关，而且还受其他两个群体策略选择的初始概率影响，实现银行与金融监管部门协同联动的理想状态，还应从参数设置入手，进而推动博弈系统策略均衡趋于理想状态。

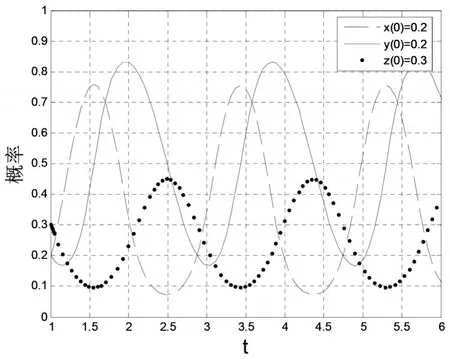
图2 银行与金融监管部门策略选择初始概率在不同情形下的均衡结果

（二）金融监管部门激励对演化博弈系统的影响

图3a显示金融监管部门激励不足时的三方博弈策略演化轨迹，考虑到银行规模差异，由此带来的协同收益分配也存在差异，此时假设p=0.8，即银行1在协同治理时获取的协同收益份额更大，但由于金融监管部门的激励不足，三方的博弈均衡并未趋于银行协同治理与金融监管部门参与监督的理想状态（图3a所示）。若金融监管部门加大激励力度，此时令r1=45、r2=35，即金融监管部门提升了激励水平。图3b显示在金融监管部门提高了激励水平后，银行选择协同治理策略更有利于自身发展，两家银行不断调整自身的策略选择，并最终选择实施协同治理策略，此时三方均衡趋于银行选择协同治理、金融监管部门采取监督的理想状态。

图3 金融监管部门激励对演化博弈系统的影响

（三）金融监管部门监督成本和惩罚力度对演化博弈系统的影响

考虑到金融监管部门的监督成本与惩罚力度对银行行为策略的影响，本文分两个阶段进行模拟，与前文一致，x0、y0、z0依次为银行1采取协同治理策略、银行2采取协同治理策略以及金融监管部门采取监督策略的初始概率。第一阶段，假设在金融监管部门监督成本较高以及金融监管部门对银行选择不协同治理策略的惩罚力度较弱情形下，令x0、y0、z0分别取0.4、0.2和0.3。图4a显示模拟此种情形，即在金融监管部门监督成本较高以及惩罚力度较弱时，银行1由于规模较大，采取协同策略获得收益份额较大，因此倾向采取协同治理策略，银行2由于规模较小等方面的原因，选择协同治理的成本高、收益低，最终会选择不协同治理策略。第二阶段，假定金融监管部门利用新型监管技术，推动监督成本下降，同时强化对银行不协同治理的惩罚措施。此时令c3=3、λ1=45、λ1=42。图4b模拟此种情形下三个群体的演化策略轨迹，当金融监管部门的惩罚力度加大和监督成本下降时，银行采取协同治理策略的意愿明显增强，博弈系统趋向金融监管部门参与监督、银行采取协同治理的理想状态。

图4 金融监管部门监督成本与惩罚力度对演化博弈系统的影响

七、结论与启示

银行理财产品刚性兑付问题事关金融市场无风险收益率、金融资源配置有效性以及金融系统稳定性。打破银行理财产品刚性兑付，推动实现“卖者尽责，买者自负”的行业交易规范，使银行理财产品回归“受人之托、代人理财”的正常轨道非常紧迫和必要。本文的三方演化博弈表明，金融监管部门监管有利于对协同要素进行控制，从而使演化博弈模型中的各要素在支配作用下实现协同效应。进一步，本文清晰推演了银行理财产品刚性兑付协同治理的演化路径。根据上述博弈分析结论与参数设定，实现银行理财产品刚性兑付协同治理，可以从三个方面着手。一是降低金融监管部门的监管成本。在银行理财产品刚性兑付治理实践中，金融监管部门应主动适应金融科技的发展趋势，更新金融监管理念和监管手段，提高金融监管的协同性和监管效率，逐步降低监管成本。监管成本的下降，使博弈双方采取协同治理策略的概率增大，有利于银行理财产品刚性兑付协同治理区域面积的扩大，从而促进银行间协同关系的建立和稳定。二是建立银行理财产品刚性兑付协同治理的激励机制。为了促使银行1与银行2更趋向于采取协同治理策略，应建立和完善银行理财产品刚性兑付协同治理机制，对采取协同治理策略的银行予以激励，有效弥补银行采取协同治理策略而带来的损失，激励力度越大，越能提高成员银行采取协同治理策略的意愿，从而增加协同域的面积，促进博弈双方采取协同治理策略的概率增大，并促使系统各成员银行协同关系的建立和延续。三是建立银行理财产品刚性兑付协同治理的惩罚机制。在银行理财产品刚性兑付协同治理实践中，应建立银行理财产品刚性兑付协同治理的监督惩罚机制，对采取非协同治理策略的银行予以惩罚。考虑将银行理财产品刚性兑付协同治理纳入宏观审慎评估体系（MPA），增加成员银行采取非协同治理策略的成本，减少成员银行机会主义行为，提高成员银行选择协同治理策略的意愿，增加协同域的面积，增大博弈双方采取协同治理策略的概率。