基于可变分频点的SMES-VRB混合储能系统在风电并网中的应用

邱晓燕，马娅妮，朱英伟，王 鹏，雷 勇

（四川大学电气工程学院，四川 成都 610065）

0 引言

近年来，随着风电的大规模利用，其并网带来的波动性及间歇性愈加不容忽视。为了解决风电消纳问题，储能技术得到大力发展［1］。单一型储能因其能量或功率限制，存在成本高或使用寿命短等不足。为了更加充分地平抑风电波动，混合型储能应运而生，将不平衡功率的低频、高频部分分别分配给能量型储能和功率型储能，有效解决了储能的经济和技术问题［2］。

相比于超级电容器储能，超导磁储能（SMES）因其零阻性、直接以磁能形式存储等超导特性，具有更高的能量转换效率、更低的自放电率、更小的电能损耗以及更快的响应速度［3-4］，且随着未来高温超导材料的发展进步，SMES的优势将使其在功率型储能技术领域发挥重要的作用，因此，性能更优的SMES 具有广阔的市场应用前景。相比于传统的蓄电池，全钒液流电池（VRB）具有效率高、寿命长、安全性好、绿色无污染等优势［5］，且随着钒矿资源的开发，VRB以其容量和功率可独立设计、扩展性强的特点有望得到大规模应用。

混合储能系统HESS（Hybrid Energy Storage System）需要通过连接变流器并入电网，变流器的控制直接影响到HESS 对风电的平抑效果。常见的控制策略包括比例积分（PI）控制、模糊控制、直接功率控制等［6-7］。PI 控制结构简单，易于实现，但控制参数依赖于精确的数学模型，难以确定；模糊控制中模糊规则的制定缺乏系统性，且当精度要求高时过于复杂；直接功率控制的响应速度快且超调小，但其开关矢量表的建立难度较大。上述方法均没有考虑系统的实时变化，无法维持复杂电力系统的稳定性。基于此，针对HESS 的变流器控制问题，本文提出了基于径向基函数RBF（Radial Basis Function）神经网络的PI 控制方法。该方法将神经网络精确、迅速的辨识功能与传统PI 控制器的简单结构有机结合，通过对HESS 模型的动态辨识，将控制参数与辨识结果进行联动调整，使得参数同步更新，从而实现系统的智能控制。目前已有很多学者将基于RBF 神经网络的PI控制应用于电力系统［8-9］，验证了该方法适用于系统的功率变换，具有抗干扰能力强且能快速及时跟踪输入信号的特点。

为了确保HESS 安全、高效运行，合理的功率分配策略至关重要。目前，应用较为广泛的风电波动功率的分解方法包括低通滤波、经验模态分解、小波包分解［10-13］等。低通滤波通过设置时间常数得到低频分量，能有效滤除风电功率中的高频波动分量。但在实际应用中并未充分考虑风电波动功率的频率特性，仅是单纯依据所需的并网功率来确定滤波时间常数的大小，缺乏理论支撑，且存在严重的滞后问题。经验模态分解通过反复求解信号的均值包络线以得到频率从高到低的子信号，依据数据自身的时间尺度特征进行信号分解，无需预先设定任何基函数，但均值包络线的选取存在端点效应，且局部极值多次跳变会导致出现模态混叠现象，使其存在较大的误差。小波包分解类似于傅里叶分析，采用多尺度分析将原信号逐层分解为高、低频分量，其不同频率间的分解结果相互独立没有混杂现象，更加适用于考虑频率差异及消纳能力的HESS 功率分配，且分解速度快，对信号的还原程度高。但目前将小波包分解应用于HESS 的研究均是参考固定频率分配功率，对储能荷电状态（SOC）的优化也仅限于限制过充过放，不能最大限度地发挥HESS 的作用。本文采用小波包分解方法，设定动态分配点，灵活分配高、低频分量，在SMES 充放电极限情况下利用VRB补充能量，使SMES 尽快恢复良好状态，为HESS 响应风电功率波动提供充裕空间。

本文首先针对HESS 并网变流器，设计了基于RBF 神经网络的PI 控制器；然后，介绍了可变分频点下功率分配的具体方法，并对SOC 优化策略进行详细说明；最后，通过与其他控制方法及分配策略进行仿真比较分析，验证了本文所提方法平滑风电功率波动的可行性。

1 HESS的结构及控制

1.1 HESS的拓扑结构及数学模型

HESS 的拓扑结构见图1。SMES 和VRB 通过各自的并网变流器并联于交流母线，并网变流器根据拓扑结构可分为电压源型和电流源型，为了稳定直流侧电压，本文选用电压源型并网变流器［14］。超导磁体通过斩波器与直流侧电容相连，而串联的钒电池组直接并联在直流电容两侧。图1 中，R、L、R*、L*为交流滤波器的等效参数；C为直流稳压电容；Lsc为超导磁体电感；UVRB为VRB的端电压。

图1 HESS的拓扑结构Fig.1 Topological structure of HESS

根据图1所示拓扑结构，可得到SMES 的电压源型变流器（VSC）部分在dq两相同步旋转坐标系下的数学模型为：

式中：eφ、iφ、Sφ（φ∈{d，q}）分别为dq两相同步旋转坐标系下电网电压、电网流向SMES 的电流、SMES 的VSC 开关函数的φ轴分量；ω为网侧电压的角频率；Udc为直流稳压电容两侧电压。

VRB 的VSC 部分在dq两相同步旋转坐标系下的数学模型为：

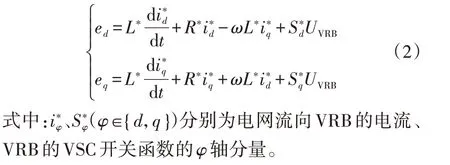
1.2 HESS的基于RBF神经网络的PI控制

HESS 的并网变流器负责储能装置对系统功率指令的跟踪，直接关系到风电波动功率的消纳效果。因此，为了提升VSC 的控制性能，采用RBF 神经网络对其控制器进行改进。

基于RBF 神经网络的PI 控制框图如图2 所示，其主要由被控对象、RBF 神经网络辨识器和PI 控制器三部分组成［15］。图中，r(k)为系统初始给定的输入，y(k)为系统的实际输出，e(k)为控制误差，三者之间的关系可表示为e(k)=r(k)-y(k)；u(k)为PI 控制器的输出，f(x)为RBF 神经网络辨识器的输出。被控对象为对象的离散化模型，表现为PI 控制器的输出与系统输出之间的关系；RBF神经网络辨识器对被控对象进行模型辨识，并将辨识结果（即Jacobian信息）反馈到PI 控制器中，PI 控制器再根据理想输出和实际输出的比较结果对控制参数进行进一步调整。

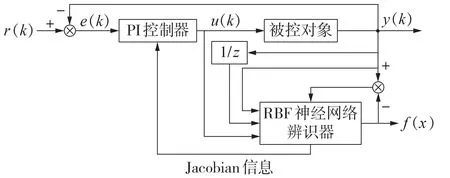
图2 基于RBF神经网络的PI控制框图Fig.2 Block diagram of PI control based on RBF neural network

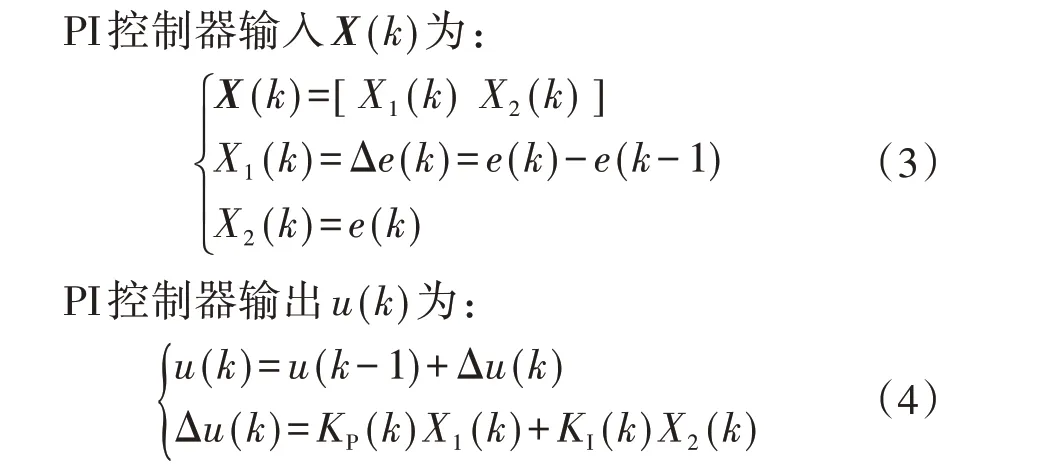
式中：KP(k)、KI(k)分别为比例系数、积分系数；Δ 表示对应变量的增量。

定义PI控制器的性能指标函数E(k)为：

为了消除有功电流与无功电流之间存在的耦合关系，对变流器均采用功率外环、电流内环的双闭环控制［17］。采用电流内环控制的目的是前馈解耦以实现有功功率和无功功率四象限独立运行，采用功率外环控制的目的是调节内环电流使输出功率跟踪参考值。为了确保功率外环应对系统变化能够快速响应指令，及时调整控制参数，对功率外环采用基于RBF 神经网络的PI 控制。以有功功率外环为例，令r(k)为有功功率参考值Pref，y(k)为实际输出有功功率P，u(k)为有功电流内环参考值id，ref，将其代入基于RBF 神经网络的PI 控制器及辨识器进行迭代计算，对PI 参数进行修正。可得变流器基于RBF 神经网络的PI控制框图如图3所示。图中，Q、Qref分别为实际输出无功功率、无功功率参考值；iq，ref为无功电流内环参考值。无功功率外环同样采取上述方法。

图3 变流器的控制框图Fig.3 Control block diagram of converter

2 HESS的功率分配

2.1 基于可变分频点的小波包分解

风电场的输出功率与并网功率之间的差值即为HESS所需平抑的不平衡功率，可见确定并网功率是HESS功率分配的前提。若并网功率过于平滑，则对储能容量要求过高；若要尽可能还原风电功率，则波动太大，难以并网。为了保证电力系统的稳定性，我国《风电场接入电力系统技术规定》明确了风电并网时其输出功率的1 min 最大波动率不得超过其装机容量的10%［18］。

小波包分解是一种以多层树状结构展开的局部化分析方法，其首先对原始信号进行分解，得到低频信号和高频信号，然后对上一层分解得到的2 种信号进行再次分解，经过n层分解后可以将原始信号分成2n个频率互不重叠且从低到高的信号分量［19］，可表示为：

式中：Pwind为风电输出功率；n为小波包分解层数；Gj为分解后的第j个子信号分量。

以1 min最大波动率为参考［20］，采用小波包分解对风电初始功率进行逐层分解，当最后一层分解中最低频部分的最大波动率恰好满足技术规定，则可确定分解层数。此时并网功率Pgrid可表示为：

根据SMES 和VRB 各自的储能特性［21］将不平衡功率的低频分量、高频分量分别分配给VRB、SMES。VRB 分配所得的功率P′VRB、SMES 分配所得的功率P′SMES分别为：

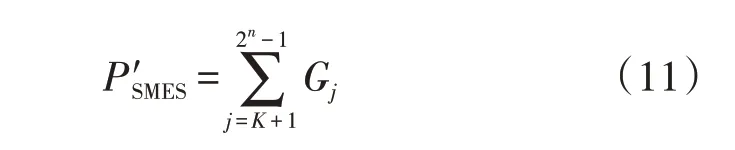
在工程实践中，风电功率入网后，1 Hz 以上的高频段波动对系统的影响很小［2］。因此，可将这部分高频分量直接输入电网由系统自身进行消纳，之后调整SMES 的功率指令，以减小SMES 的充放电次数。

设储能充放电优先级X∈{1，2，3，4，5}为中间变量，根据界限值对SOC 进行区域划分以对应不同的充放电优先级，如图4 所示。图中，SSOC，min、SSOC，max分别为SOC 下限、上限值；SSOC，down、SSOC，up分别为SOC 较低限制值、较高限制值。

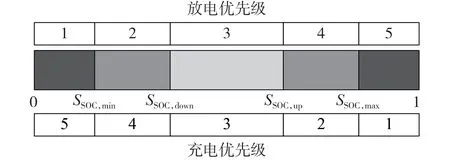
图4 充放电优先级设定Fig.4 Setting of charging and discharging priority

分频点K由2 种储能的充放电优先级决定，可表示为：

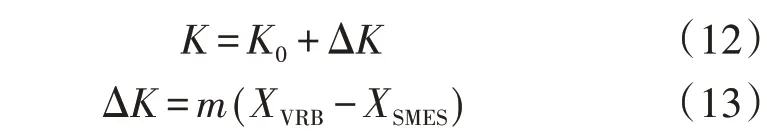
式中：K0为分频点的初始值，可通过综合考虑SMES容量及VRB 响应频率二者对应的风电小波包分解结果确定，本文仿真根据所选风电分解结果（即分解层数为6层，得到32个子分量）设定K0=9；XVRB、XSMES分别为VRB、SMES的充放电优先级；m为修正系数，可变分频点的原理类似于滑动变阻器，为了灵活划定分频点的变化范围，本文设置m为常数。本文仿真研究中设置m=1，具体选定方法及不同m取值下的仿真对比结果见附录A。

根据不同的储能SOC 确定动态变化的分频点，基于此可以得到SMES 和VRB 的初始功率分配参考值。

2.2 基于充放电优先级的功率优化

考虑到XVRB-XSMES可能为0的情况，还需根据充放电限制进行优化分配，此外还可以利用储能自身的特点稳定SOC。进一步功率优化策略的步骤具体如下。

1）当进行初始功率分配时，若XVRB=XSMES，则需考虑过充过放问题，对功率进行如下限制：

传统作文教学中存在以下弊端：第一，教师结合写作题目进行范文阅读和讲解，严重限制了学生的想象力，导致学生在写作时感到无话可说，写作学习兴趣降低；第二，常常选用固定的内容和题目，导致学生写作千篇一律，描写母爱，最常使用的典故就是母亲冒着大雨背孩子去看病等，内容老旧毫无新意；第三，不少学生为了在考试中取得高分，作文胡乱编写。这种作文教学严重失去了教育意义，不利于学生身心健康成长。

式中：P′为初始参考功率；Pfinal为优化分配后储能的最终参考功率；c为SOC 修正系数；SSOC为储能实时SOC；PHESS为不平衡功率。由于此处的功率限制设定储能独立调整，所以储能充放电优先级X及Pfinal、P′不区分储能类型（即变量未带下标VRB、SMES）。当X=3，4，5 时，表示储能具备充裕空间，应积极出力，因此不进行功率限制。

2）当进行初始功率分配时，若XVRB≠XSMES，则需考虑极限SOC 下不利于下一时刻储能充放电的问题，为了使储能尽量保持良好的SOC，需要合理安排储能之间进行功率转移，即使优先级高的一方承担优先级低的一方的充放电任务，并对优先级低的一方进行功率补充，使其反向充放电，尽快恢复最佳SOC。

由于VRB 具有容量大、响应速度快以及使用寿命长的特点，其SOC 较易稳定；而SMES 属于功率型储能，其SOC 波动大，容易陷入极限区域。因此，利用VRB 对SMES 进行功率援助支撑，功率调整规则如下。

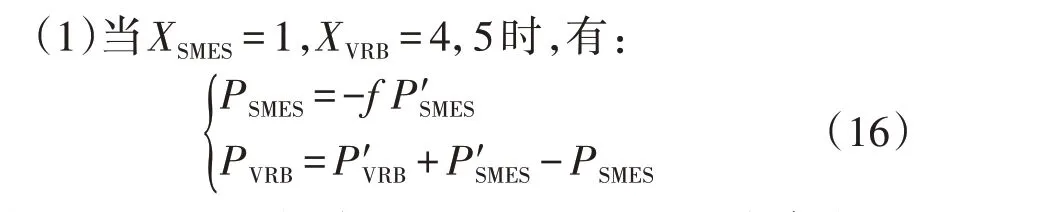
式中：PSMES、PVRB分别为SMES、VRB 的最终参考功率；f为限制系数，其值与SMES 额定容量和VRB 额定容量的比值呈负相关。

（2）当2 种储能的充放电优先级取值为1 或2，且XVRB≠XSMES时，按照2种储能的充放电优先级相同时的功率限制处理，SMES 和VRB 单独调整，互不影响。

（3）当XSMES≥3 且XVRB≥3 时，表明储能SOC 良好，无需进一步优化，直接输出初始分配所得的参考功率。

综上所述，风电功率分配主要包括以下2 个步骤：①利用储能可用空间适时改变分频点，由小波包分解方法灵活充分地分配得到初始参考功率；②针对储能的不同SOC，借助VRB 能量型储能的优势，对SMES 功率进行补充以将其SOC 维持在稳定水平。HESS功率分配流程图如图5所示。

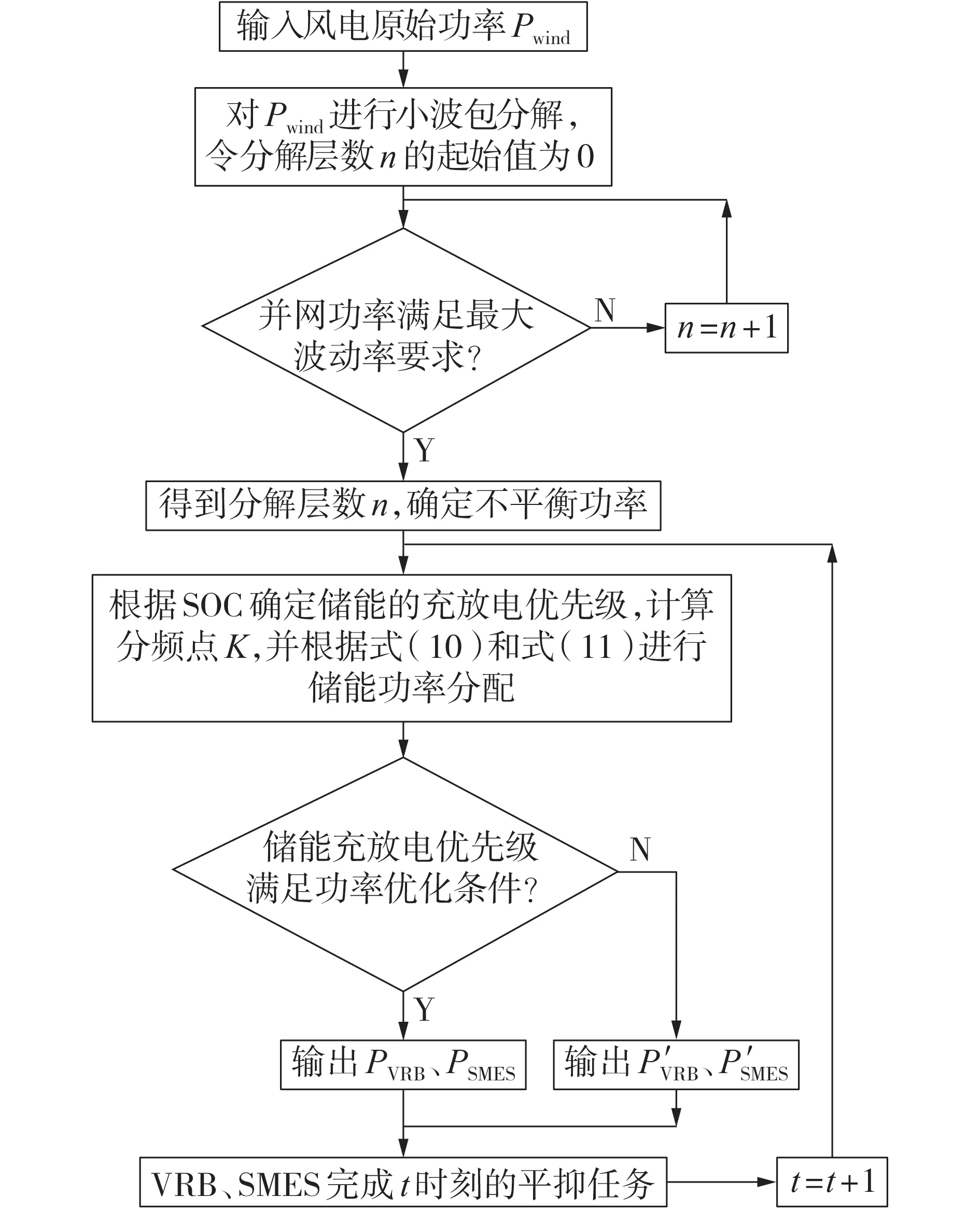
图5 HESS功率分配流程图Fig.5 Flowchart of HESS power distribution

3 仿真分析

本文采用MATLAB／Simulink 仿真软件对所提控制方法及功率分配策略进行仿真分析。基于RBF神经网络的改进PI 控制器部分采取S 函数形式编写；功率分配通过Function 函数编辑器完成。因本文侧重于HESS 的功率分配协调控制，未涉及容量配置，故在仿真中假定预设容量能够恰好满足不平衡功率的平抑任务需求，HESS 的仿真参数见附录B表B1。

为了验证本文所提基于RBF 神经网络的PI 控制器的有效性，对其并网变流器分别采用传统PI 控制器和本文所提PI 控制器进行对比分析。SMES 的控制效果与VRB 类似，因此以VRB 为例进行分析，使VRB 运行在单位功率因数下，即只接受有功功率指令，无功功率指令为0。对有功功率设置阶跃指令，0、0.2、0.4 s 时的有功功率分别为0、50、-30 kW。VRB 有功功率及电池端电压的跟踪结果如图6 所示。由图可以看出，本文所提PI 控制器在跟踪功率指令时更及时、更准确，电池端电压响应更迅速、超调量更小。

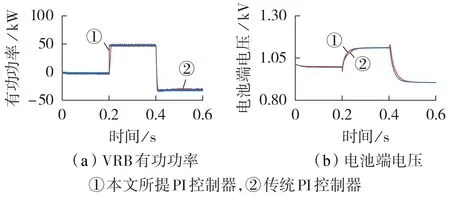
图6 VRB的仿真结果Fig.6 Simulative results of VRB

为了验证本文所提功率分配策略的正确性，对配置HESS 的含风电电网进行仿真分析。风电输出功率取自某风电场的实测数据，以1 s 为时间间隔进行采样，共采样2 000 个点，风电机组的额定功率为2 MW。当小波包分解层数为6 层时，并网功率的1 min 最大波动率为8.4%，恰好满足波动率要求。因此，选择对原始风电功率进行6 层分解后得到并网功率。原始风电功率及采用低通滤波和小波包分解所得并网参考功率见图7。由图可以看出，小波包分解所得并网参考功率更加平滑，更贴合原始风电功率，且没有延时。

图7 原始风电功率及并网参考功率Fig7 Original wind power and grid-connected reference power

将本文所提功率分配策略（可变分频点并基于储能充放电优先级）与策略1（基于低通滤波和储能充放电优先级的功率分配策略）、策略2（基于一般小波包分解和储能充放电优先级且分频点固定的功率分配策略）进行对比仿真，且控制方法均采用基于RBF 神经网络的PI 控制器。储能SOC 的分区设置见附录B 表B2，3 种策略下储能的SOC 结果如图8所示。

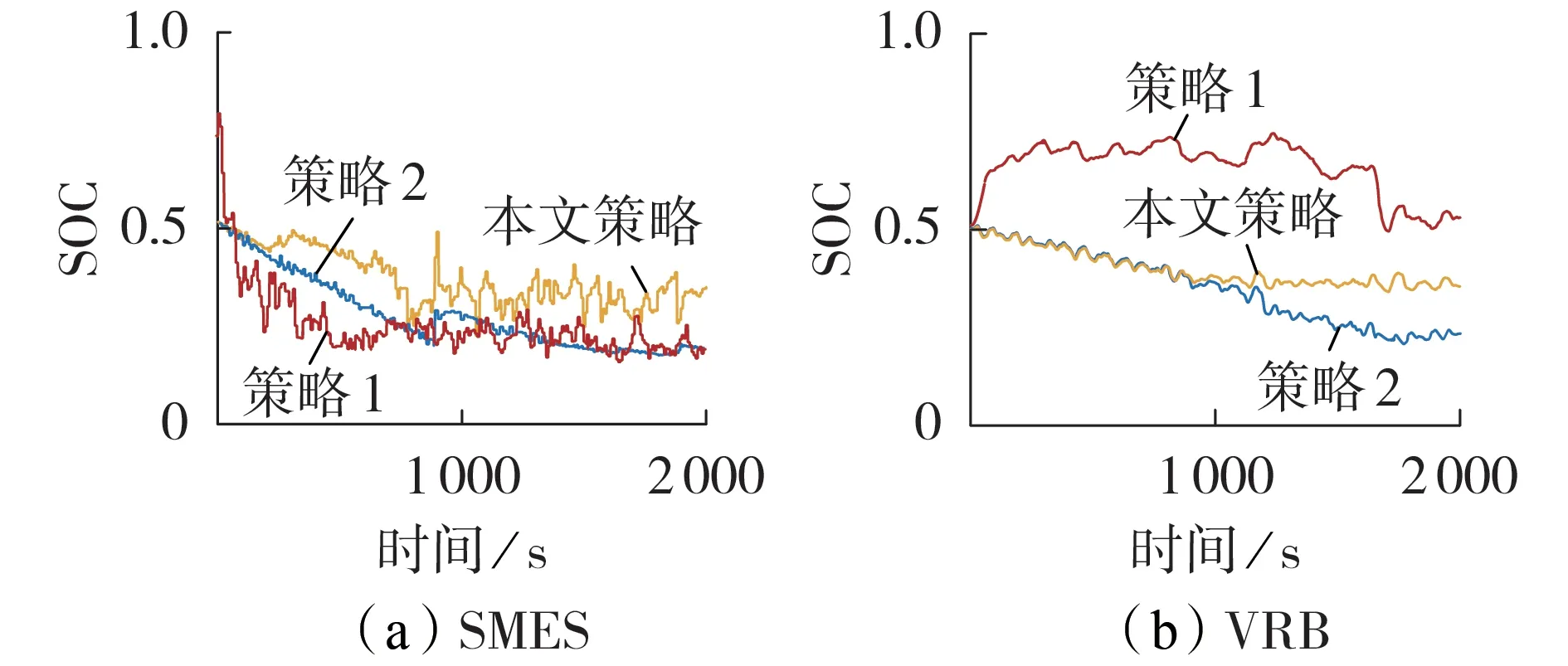
图8 3种策略下储能的SOCFig.8 SOC of energy storage under three strategies

由图8（a）可以看出：策略1下SMES的SOC在仿真起始时波动较大，这是因为低通滤波的滞后现象导致并网功率一开始远小于风电功率，故对储能大幅充电，SMES得到的功率指令瞬间过大超出了其容量限制，无法稳定跟踪，且100～200 s内SMES分配得到的功率指令放电部分多于充电部分，因此造成SOC 先骤升后骤降；策略2 下SMES 的SOC 下降也较为明显，虽然SOC因优化控制及时稳定了下降趋势，但始终在其SOC的下限值处波动；相较而言，本文策略下SMES 的SOC 稳定效果最佳。由图8（b）可以看出：策略1 下并网功率延迟的问题导致VRB 大幅度充电，进而使得SOC 大幅上升；策略2下VRB 的SOC下降幅度较大，最后稳定在VRB 的SOC 下限值处；而本文策略下VRB的SOC略微下降之后恢复平稳。

本文策略下分频点的变化情况如图9 所示。由于VRB 和SMES 的初始SOC 均为0.5，在充放电过程中SOC变化较为平稳，所以分频点也相对稳定；随着功率平抑过程的进行，储能的SOC发生变化，分频点也随之改变。

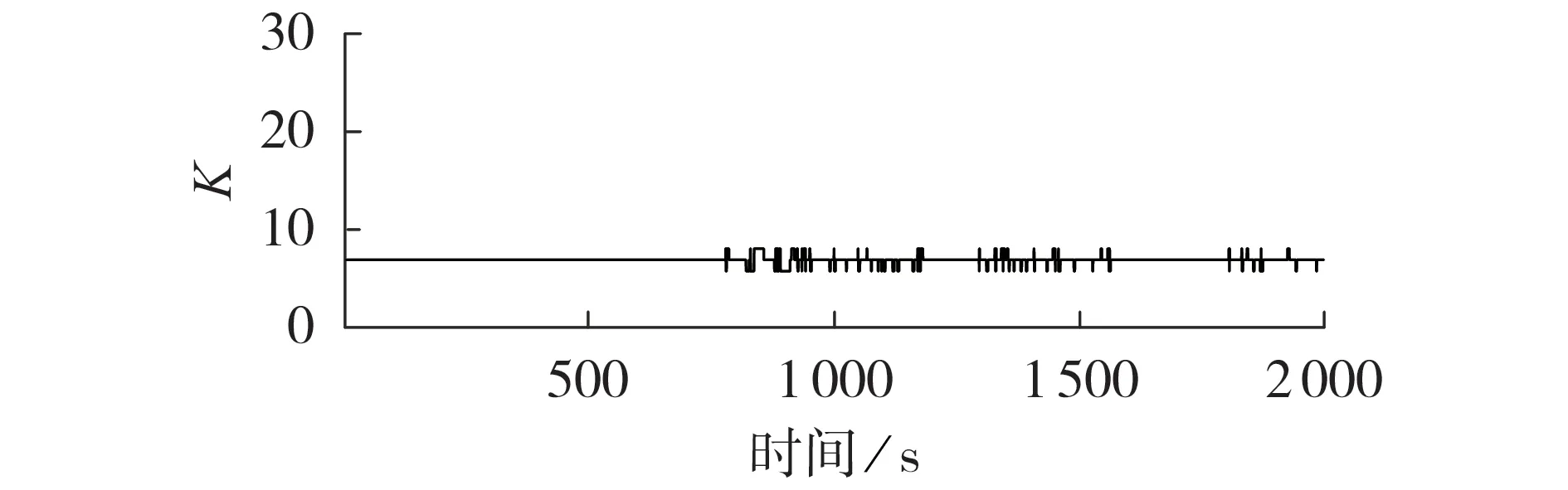
图9 可变分频点的变化情况Fig.9 Change of alterable frequency division point

在本文策略下SMES和VRB 的输出功率如图10所示。由图可以看出，SMES 响应高频小幅功率指令，VRB 响应低频大幅功率指令，HESS 的优势得以体现。

图10 HESS的输出功率Fig.10 Output power of HESS

为了综合验证本文所提控制方法对风电波动的平抑效果，将其与方法1（低通滤波+PI 控制器，并基于充放电优先级进行功率分配）、方法2（小波包可变分频点+PI控制器，并基于充放电优先级进行功率分配）进行对比仿真，3 种方法的实际并网功率对比如图11 所示。由图可知，相比于其他控制方法，本文所提控制方法下的实际并网功率更加平滑，且能较好地跟踪原始风电功率的波动。

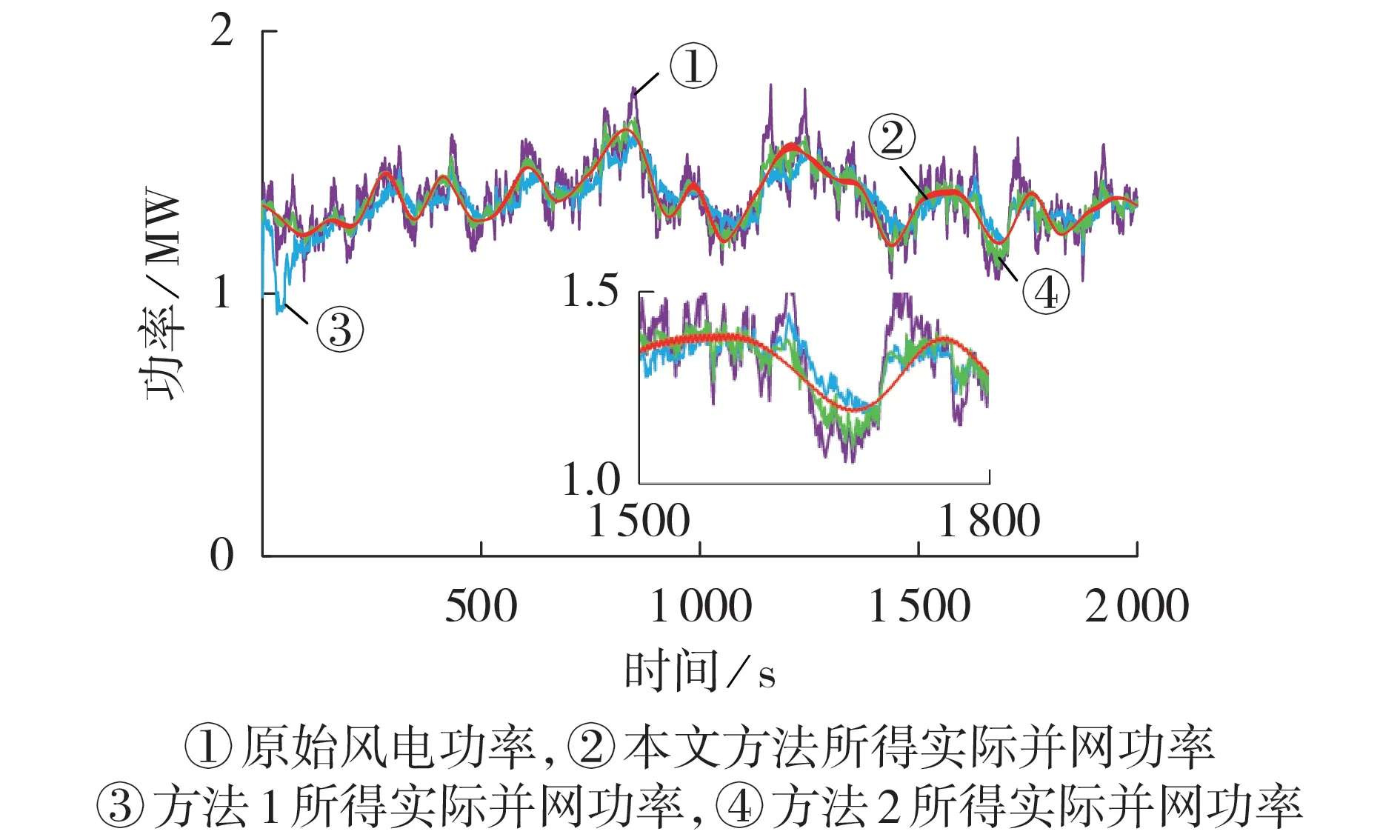
图11 3种方法的实际并网功率对比Fig.11 Comparison of actual grid-connected power among three methods

对上述控制方法下的实际并网功率、原始风电功率及经6 层小波包分解所得理想并网功率的波动率进行计算，结果如表1 所示。由表可知，本文所提控制方法所得实际并网功率的1 min 最大波动率仅为9.1%，虽然不及理想并网功率的波动率，但已满足工程实际的并网要求。

表1 波动率对比Table 1 Comparison of volatility

4 结论

针对风电消纳问题，本文研究了HESS 在风电并网中的应用，在结合SMES 和VRB 各自优点的基础上，设计了基于RBF 神经网络的PI 控制器，可根据HESS 实时功率在线调整控制参数，有效控制储能系统进行快速、精确的功率吞吐，克服了传统PI控制器控制参数固定且不易确定的不足；在风电功率分配中，对小波包分解法进行了优化，采用动态可变的分频点，可根据储能的实时SOC 改变分配至不同储能的参考功率，最大限度地利用了储能空间且避免了储能过充过放，并充分发挥了VRB 容量大、充放电次数多的特性，使其对SMES 进行功率补充，有效稳定了储能的SOC，保障下一时刻充放电任务的顺利完成，有利于更好地实现风电功率波动的平抑目标。仿真结果验证了本文所提HESS 控制方法及功率分配策略的有效性及可行性。

附录见本刊网络版（http：//www.epae.cn）。