考虑风电接纳水平及负荷增长的海上风电场多阶段规划

2022-02-21江岳文张金辉

电力自动化设备 2022年2期

江岳文，张金辉

（1. 福州大学电气工程与自动化学院，福建福州 350108；2. 智能配电网装备福建省高校工程研究中心，福建福州 350108；3. 福州大学综合能源规划与优化运行研究中心，福建福州 350108）

0 引言

由于规划、运营缺乏经验以及政策方案不够完善，在我国海上风电发展的过程中遇到了包括造价成本高、投资风险大以及存在并网运行等问题。在电力市场改革背景下，海上风电的高成本与不确定性收益之间的矛盾也将更加尖锐。而对海上风电场的合理规划以及对电力市场环境下投资效益的准确评估不仅能够提升投资回报率、降低投资风险，也能够促进海上风电的消纳以及优化含风电电力系统的运行，是解决现阶段海上风电发展所面临问题的有效途径。

目前针对风电场的装机容量优化、布局优化等一系列规划问题已取得了一定的成果。对于风电场布局优化问题，文献［1-2］在基于尾流效应的影响下，以发电量最大或度电成本最小为目标实现对风电场风机布局的优化。对于风电场的装机容量优化问题，文献［3］以总效益最大为目标实现了风电装机容量的优化，但该研究是以风电全量接纳为前提，忽略了系统对风电接纳能力的限制。实际上，风电接纳水平是决定风电场装机容量的主要因素［4］。文献［5-6］从调峰角度评估风电接纳能力，构建考虑适当弃风的风电场装机容量优化方法；文献［7］从调度经济环保的角度评估风电接纳水平，提出风电场装机容量分层优化方法。但随着电力市场的发展，未来我国海上风电项目将通过竞争方式进行配置以及确定上网电价［8］，上述文献装机容量优化方案中的静态负荷和固定电价模式将无法适应新形势下的发展，因此亟需对电力市场环境下的海上风电场规划问题展开深入研究，充分发挥市场在资源配置中的作用，并利用电力市场的交易机制有效提升新能源发电在电能供应中的比例［9］。

此外，现有风电场或者含风电的电力系统规划方案大多关注短期内的投资经济性，而忽略了中长期电力负荷持续增长导致初始规划方案与中、后期运行之间缺乏有效衔接的问题。多阶段规划是解决单阶段规划所面临问题的有效途径［10］。文献［11］建立风机的多阶段选址定容规划模型，但是其每个阶段的投资时间以及风电结算电价均为固定值；文献［12］提出风火电打捆发电系统的多阶段规划模型，但是总装机容量已经事先给定，而且没有对风电售电价格和投运时间进行优化；文献［13］以分场景模拟多阶段规划模型未来年负荷需求和投资成本的变化情况，有助于提高规划的协调性，但是每个阶段的时间跨度为定值。为了进一步提升多阶段规划方案的优越性，应该考虑投资时段和市场环境下的价格波动。

综上，本文结合海上风资源特性和海上风电场单机容量大、总投资成本远高于陆上风电场等特点建立海上风电场多阶段协调规划模型。首先，在模型中考虑运行周期内负荷需求的变化，以日前市场竞价清算模型评估区域电网对海上风电的最大接纳水平和电价水平；其次，以日前市场所获得的风电接纳量和上网电价为基础，将规划周期分为若干个阶段，以每个阶段的投资年份、风机数量、每台风机的位置以及所属投资阶段为优化变量，建立以净收益最大化为目标的海上风电场多阶段规划模型；最后以对比方案验证本文所建立的规划模型的有效性和优越性。

1 基于日前市场的风电最大接纳能力评估

在未来电力市场逐步建立和完善的背景下，应充分利用电力市场的交易机制提升可再生能源在电力供应中的比例，解决电力市场环境下可再生能源的消纳问题。考虑到日前市场是电力现货市场的重要载体，通常具有最大的交易量，本文将以日前市场作为交易平台，评估区域电网对海上风电的最大接纳水平并获得清算价格，以此作为海上风电场多阶段规划的重要基础。

1.1 日前市场竞价清算模型

以满足节点的负荷需求为前提，构建以购电成本最低为目标的日前市场竞价模型，需要优化的变量包括常规发电机组在日前市场调度时段中的有功功率和海上风电最大接纳水平，其目标函数可表示为：

1.2 约束条件

2 海上风电场多阶段规划模型

2.1 多阶段规划方案的基本架构

设海上风电场的规划期限为Tpla，共分为n个阶段，规划期限和阶段数可由设计者事先划定，并以Ti（i=1，2，…，n）表示第i个阶段，多阶段规划模型的框架示意图如图1 所示，其不同阶段的规划模型均一致。图中，gi（i=1，2，…，n）为第i个阶段的投资年份；Eset，i（i=1，2，…，n）为第i个阶段配置的风机装机容量，其值由隶属于第i个阶段的风机总数与风机额定容量Pe相乘获得，其是在已投运风机Eset，1、Eset，2、…、Eset，i-1基础上的新增装机容量。

图1 海上风电场多阶段规划示意图Fig.1 Schematic diagram of multi-stage planning ofoffshore wind farm

在n个阶段中，每个阶段的投资年份为待优化的变量，可记为序列g：

投资年份是指风电机组建设完成投入使用的年份，以g1=1表示第1年为第1阶段的投资年份，作为参考值，这使得每个阶段的时间间隔不定，为变量，其值由gi-gi-1确定。假设第i个阶段投入的风机在第i-1 个阶段最后一年年末已完成建设，则第i个阶段投建风机的总运行时长为Tope-gi。

海上风电场风机总数为N台，属于待优化的整数变量。对应N台风机位置横、纵坐标的序列[x，y]可表示为：

式中：xi、yi（i=1，2，…，N）分别为第i台风机位置的横、纵坐标。将坐标变量定义为连续变量，以便风机位置坐标能在规定海域范围内充分寻优。

每台风机安装所属的投资阶段S为整数优化变量，可表示为：

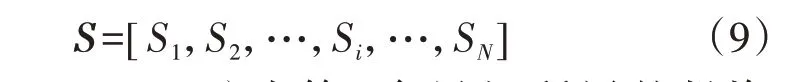
式中：Si（i=1，2，…，N）为第i台风机所属的投资阶段。

对应各阶段装机容量的序列Eset表示为：

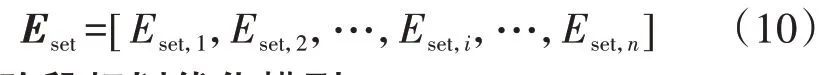
2.2 多阶段规划优化模型

2.2.1 优化目标

多阶段规划的目标为项目拟投建运行周期Tope中的净收益最大化，可表示为式（11）。各年的售电收益与成本均通过现值系数折算至运行周期初始年。

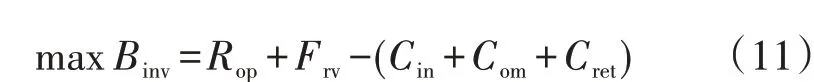
式中：Binv为海上风电场在运行周期中的净收益，Rop为海上风电场的发电总收益，Frv为风机在运行周期末的折余价值，Cin、Com分别为风机投资总成本、运行维护总成本，Cret为风机退役成本，上述收益与成本均折算至初始年。

待优化整数变量包括风机总数N、每个阶段的投资年份gi、每台风机所属的投资阶段Si；待优化的连续变量包括每台风机位置的横坐标xi和纵坐标yi。

1）海上风电场的发电总收益。

当海上风电场达到运行周期时，风机需要按计划退役，会产生拆卸、运输、后续处理、海域复原等较为高昂的费用。海上风电场的风机退役成本可表示为：

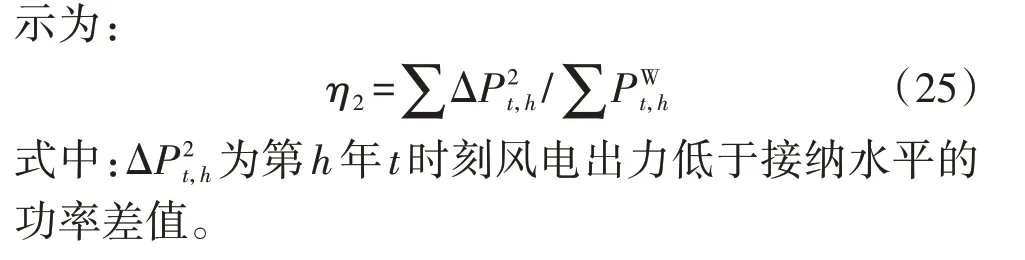
3 模型求解

采用直流潮流分析获得风电最大接纳水平和节点电价的日前市场竞价模型。对该线性规划问题可以基于MATLAB 平台，通过Yalmip 编程并调用CPLEX 进行高效求解，得到运行周期中各时段常规发电机组的出力水平及风电最大接纳水平，再进一步求解上述线性规划问题的对偶模型，可以求得海上风电的节点电价，并将其作为海上风电的清算电价。

由于尾流模型的引入，本文所提出的多阶段规划模型属于具有高维非线性的混合整数规划问题，无法采用以梯度为基础的传统优化算法对其进行求解，而群体智能算法是一种较好地兼顾求解效率和优化结果的非线性问题求解方法。本文采用改进的量子粒子群优化（IQPSO）算法［17］对多阶段规划模型进行求解，其特有的粒子更新公式能够大幅增强算法的搜索能力，提高求解效率。式（22）所示的机组间距约束为非线性约束，可以通过在原目标函数式（11）中增加惩罚函数形成新的增广目标函数，可表示为：

模型求解的总体流程图如图2所示。

图2 模型求解流程图Fig.2 Flowchart of solving model

4 算例分析

4.1 算例参数及场景设置

设定海上风电场分为3 期规划投资，规划期限Tpla=12 a；项目拟投建运行周期Tope=25 a；风机周期寿命Ttur=25 a；选取长6 km、宽7 km 的规划海域作为风机的布置区域，其海面粗糙长度为0.05 m；风速和风向的原始数据来源于美国国家新能源实验室Longford 测量站数据。风机参数如附录A 表A1所示；取风机单位容量投资成本的拟合函数系数a=0.028 3、b=-0.124、c=0.137 2；风机单位容量的退役成本为200 万元／MW；折现率r=8%；设备净残值率δ=6%。

以IEEE 30 节点测试系统为例，风电接入节点10；6 台常规发电机组的运行和报价参数分别如附录A 表A2 和表A3 所示（为了突出本文主要内容，本文中报价设为固定参数，但是本文模型和方法均适用于动态报价）。选择4 个季节的典型日负荷数据（标幺值）如附录B 图B1 所示，以此表示年负荷变化曲线。考虑到海上风电大多接入沿海经济快速发展的区域，其长期电力负荷呈现“单边上扬”的快速增长模式，因此假设未来年的区域电网总负荷具有如附录B 图B2 所示的变化趋势，由此考虑中长期负荷变化对指导电力规划的重要意义［18］。取图B2 中的负荷高增长模式作为基础案例，其投资年份最大负荷值为350 MW。

4.2 多阶段规划结果与分析

为了验证本文所提出的多阶段规划方案的有效性，本节算例设置2 种场景进行比较：场景Ⅰ，不考虑建设时序，以单阶段规划方法在投资年份规划装机容量及机组位置；场景Ⅱ，考虑多阶段建设时序，采用本文所提出的多阶段规划方法优化各阶段的投资年份、装机容量及机组位置。2 个场景的其他条件一致。

以项目拟投建运行周期Tope中不同负荷水平为基础，对以购电成本最低为目标的日前市场竞价模型进行求解，获得项目拟投建运行周期Tope中每个季度典型日的风电最大接纳水平。以投资年份为例，每个季度典型日的风电最大接纳水平波动曲线如图3所示，其余年份具有相似特性。

图3 投资年份风电接纳水平Fig.3 Wind power accommodation level in investment year

以获得最大风电接纳水平以及节点电价为基础，进一步求解场景Ⅰ和场景Ⅱ对应的规划方案，结果如附录A表A4所示。2个规划方案的最优布局如图4 和图5 所示，图中X、Y分别表示风机位置的横、纵坐标。单阶段规划方案的结果是在投资年份安装35 台风机，多阶段规划方案的结果是在第1 个阶段的最优投资年份（即第1 年）安装21 台风机，在第2 个阶段的最优投资年份（即第6 年）安装15 台风机，在第3 个阶段的最优投资年份（即第12 年）安装13 台风机。虽然多阶段规划方案的总投建风机数量相比单阶段规划方案增加了14 台，但多阶段规划方案中有较多风机属于第2、3 个阶段投资，该阶段风机的投资成本已较投资年份有了较大幅度的下降，运行维护时长也较单阶段规划方案有所缩短，这使得多阶段规划方案与单阶段规划方案在风机投资总成本和风机运行维护总成本上的差值仅分别为0.1、0.02 亿元。2 个规划方案的主要区别体现在海上风电场的发电总收益、风机在运行周期末的折余价值以及风机退役成本：相较于单阶段规划方案，多阶段规划方案的海上风电场的发电总收益提升了2.32 亿元，风机在运行周期末的折余价值增加了1.2亿元。综合考虑收益与成本后，多阶段规划方案获得的最高净收益为14.75亿元，相比单阶段规划方案获得的最高净收益10.89 亿元提升了35.4%，体现了多阶段规划方案在提升投资回报率上的优势。

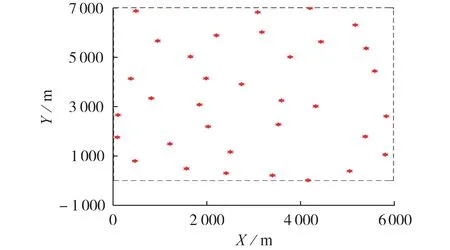
图4 单阶段规划最优布局Fig.4 Optimal layout for single-stage programming

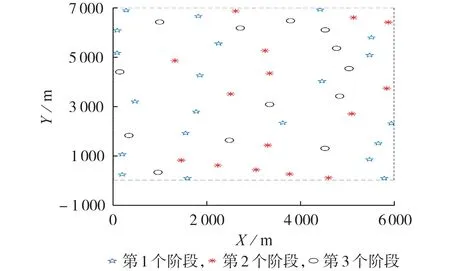
图5 多阶段规划最优布局Fig.5 Optimal layout for multi-stage programming

以夏季典型日为例，图6（a）、（b）分别给出了第1 个阶段最优投资年份（即第1 年）和第3 个阶段最优投资年份（即第12年）该日风电最大接纳水平和2个规划方案下海上风电场的出力，其余季度也具有相似特性。表1为2个规划方案对风电的消纳对比。由表1 可知，不论是在阶段典型日还是在完整的运行周期中，多阶段规划相比单阶段规划均具有更低的弃风率和欠风率，取得了更好的运营效果。

图6 第1个和第3个阶段夏季典型日风电接纳水平和风电出力Fig.6 Wind power accommodation level and wind power output in typical day of summer at Stage 1 and 3

表1 风电消纳情况对比Table1 Comparison of wind power accommodation condition

综上，考虑多阶段规划的场景Ⅱ比仅考虑单阶段规划的场景Ⅰ具有更好的运营经济性，通过对海上风电场进行多阶段规划，既能避免规划前期因超前投资而造成机组设备的冗余和资源的浪费，也能较好地满足规划中、后期因风电接纳水平提升对风电出力的需求，由此也体现了海上风电场多阶段规划相较于单阶段规划方案的优越性。

4.3 负荷增长模式的影响分析

在海上风电场多阶段规划模型中，负荷显著影响风电最大接纳水平，进而决定了多阶段规划方案的优化结果。因此，本节将对比附录B 图B2 中3 种负荷增长模式下海上风电场多阶段规划方案的结果，如附录A表A5所示。

不同负荷增长模式下的风机最优投资年份和最优装机数量不尽相同，但呈现出一定的规律特点：当区域电网负荷处于高增长模式时，最优装机数量最多为49台，第1个阶段与第2个阶段间隔5 a，第2个阶段与第3个阶段间隔6 a，阶段间的时间间隔最长，获得的总净收益最大；随着负荷增长率的降低，各阶段获得的最优投资年份逐步向投资年份靠近，阶段间的时间间隔逐步缩短，前、中期装机的比例增加，总净收益下降。产生上述现象的主要原因是：当前、后规划阶段存在高负荷差时，风电最大接纳水平也存在较大差距，少量的装机已能满足前期所需的供能水平，若前期装设过多风机，则不仅会大幅增加投资成本，也会产生大量弃风，不利于提升风电场的经济效益；中、后期投建的风机能弥补运营过程中由于装机容量不足而缺少的供能水平，增加售电收益，且后期逐步下降的风机投资成本也是促进收益增加的有利因素；但随着负荷模式发生变化，负荷增长率降低，前、后期负荷差距缩小，这使得风电最大接纳水平也逐步接近，前、中期的装机能产生更高的运营收益，促进各阶段投资年份的提前和前、中期装机比例的提升。