基于SSA-PNN的电力变压器故障诊断
2022-02-21卫永鹏王胜利苏益辉
张 鑫,王 衡,卫永鹏,王胜利,苏益辉
(1.国网甘肃省电力公司检修公司;2.兰州理工大学 电气工程与信息工程学院,甘肃 兰州 730050)
0 引言
当前,我国主要采用改良三比值法进行变压器故障诊断,但在实际的工程应用中,往往受限于改良三比值法处理故障样本数据临界值的不确定性[1]。在油中溶解气体浓度较低时,难以准确判别变压器的状态,在面对潜在性故障时,难以确定故障是否发生并判断相应的故障类型。因此,在改良三比值法的基础上提出一种新的变压器故障诊断方法有重要的实际工程意义。
近年来,随着人工智能技术的不断发展完善,越来越多的机器学习算法被不断提出并在变压器故障诊断领域得到了应用,例如模糊聚类、堆栈自编码器、卷积神经网络等[2]。文献[3]通过支持向量机对油中溶解气体进行分析,利用高维空间下气体的不同特性进行变压器故障诊断,但对样本数量有一定限制。文献[4]通过对特征数据的模糊化处理,可以准确判断变压器故障类型。但是模糊规则制订的优劣在相当程度上依赖于专家经验。文献[5]建立了基于深度自编码器的诊断模型,可以有效解决部分特征数据无法分类的问题,但是该网络模型的完善依赖于大量的样本数据训练,因此不适用于特征数据较少的情况。文献[6]采用BP神经网络诊断变压器故障,通过输入特征数据可以准确的对故障类型进行判断,但是由于BP神经网络是一种基于梯度下降的算法,对网络参数设置比较敏感,而且容易陷入局部最优解,当样本特征数量较多或者样本间关系复杂的时候,容易导致过拟合。麻雀搜索算法(Sparrow Search Algorithm, SSA)寻找全局最优精确度高,在收敛速度和稳定性方面相对于现有的算法都有一定程度的提升,可以有效避免BP神经网络等算法寻优速度慢,容易过拟合,陷入局部最优等缺点[7]。
该文采用麻雀搜索算法优化概率神经网络的变压器故障诊断方法,将SSA算法应用到PNN网络的参数选择中,以PNN样本集中分类错误率最低为优化目标,选择最优的平滑因子,建立SSA-PNN故障诊断模型,并通过算例分析验证了该方法的有效性[8]。
1 概率神经网络和麻雀搜索算法
1.1 概率神经网络
PNN由D.F.Specht在上世纪九十年代提出,是一种以统计学原理为基础的人工神经网络,常用于处理非线性模式分类问题。PNN的网络模型如图1所示。
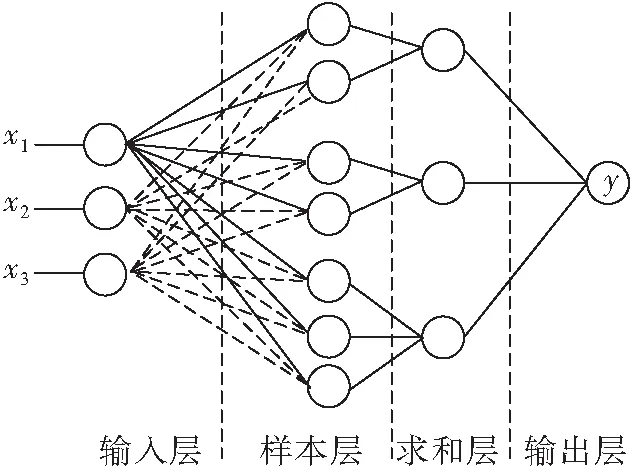
图1 PNN网络结构
PNN网络由4部分组成,从左至右分别是输入层、样本层、求和层、输出层。首先将输入数据转换成向量,在输入层中通过与训练样本向量做差并求绝对值可以得到两个向量之间的距离,接下来,将做差后的向量送至样本层中,样本层节点的数量与样本的数量相同[11]。该层中第i个类别对应第k个神经元所对应的函数为:
(1)
式中:i=1,2,...,N,N为训练样本标签值的数量;d为训练样本的特征值的数量;σ为平滑因子,是PNN网络的关键参数[12]。
样本层通过判断各个向量与不同类别之间的关系,以相关度为标准,将不同类别聚集,并将结果输出至求和层,求和层节点数等于样本特征值的数目,计算样本层内属于同一类型的节点的个数并做加权平均,其公式为:
(2)
式中:vi为第i种标签值的输出;L为第i类神经元的数量[13]。
将求和层计算的最大值送入输出层,公式为:
y=argmax(vi)
(3)
通过求和层的竞争传递函数得到某一样本隶属于各个类别的概率,将概率最大的类别作为输出的结果[14]。
1.2 麻雀搜索算法
麻雀搜索算法在2020年被提出,是一种基于麻雀群体行为的算法。
种群中的个体通过发现者和加入者两种行为决策获取食物,种群中发现者和加入者所占的群体比例是固定的,通常情况下,发现者是种群中健康值较高的个体,并担负起为种群成员探索食物来源的任务。加入者会密切监视发现者并积极抢夺食物以增加自己的健康值。当发现者发现天敌时,通过报警信号提醒群体成员躲避危险,当报警值大于安全阈值时,种群会迁移至其他位置。在种群的每次迭代的过程中,发现者的位置更新公式为:
(4)
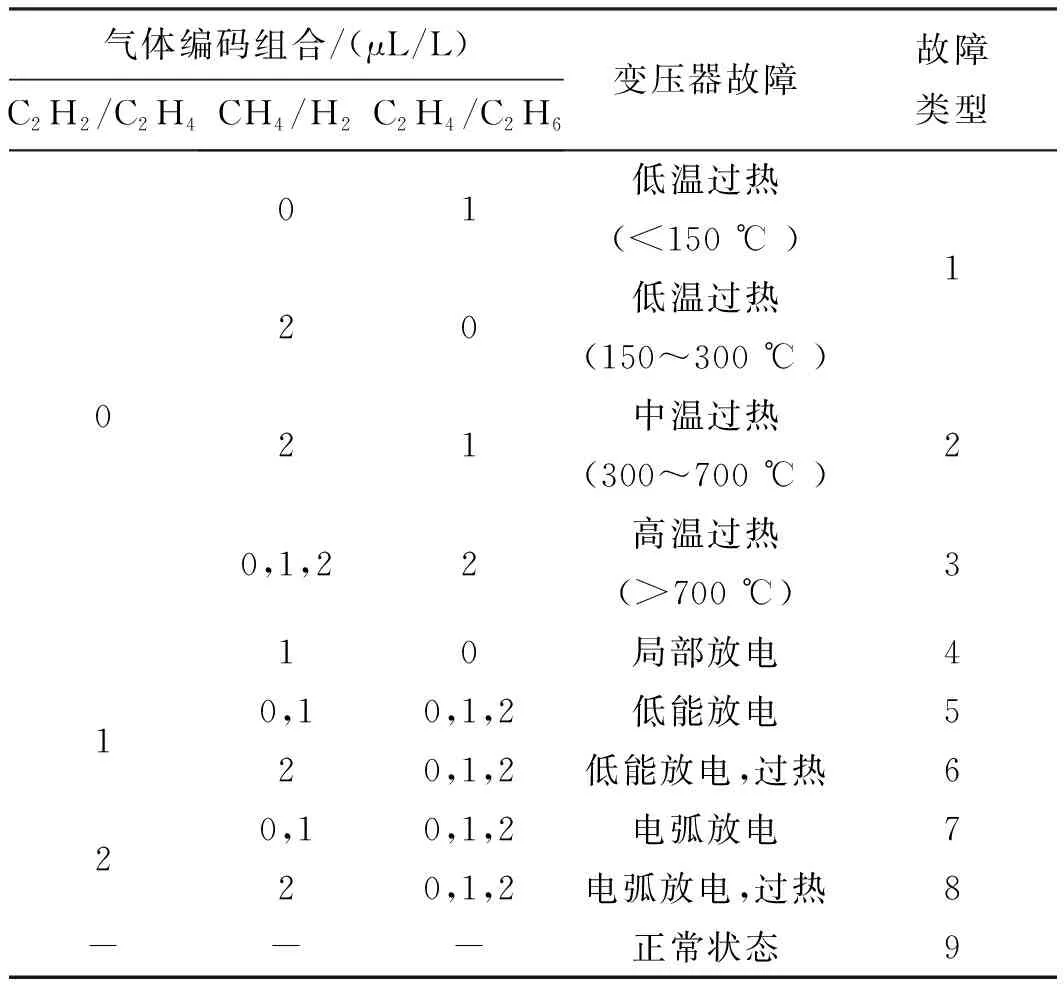
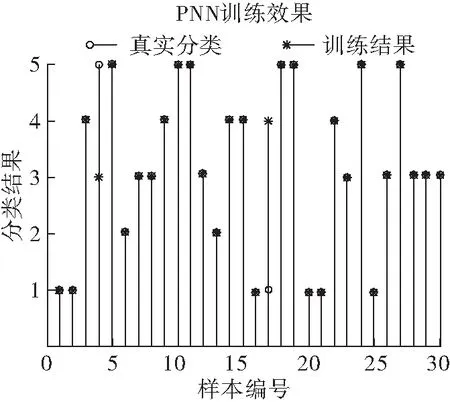
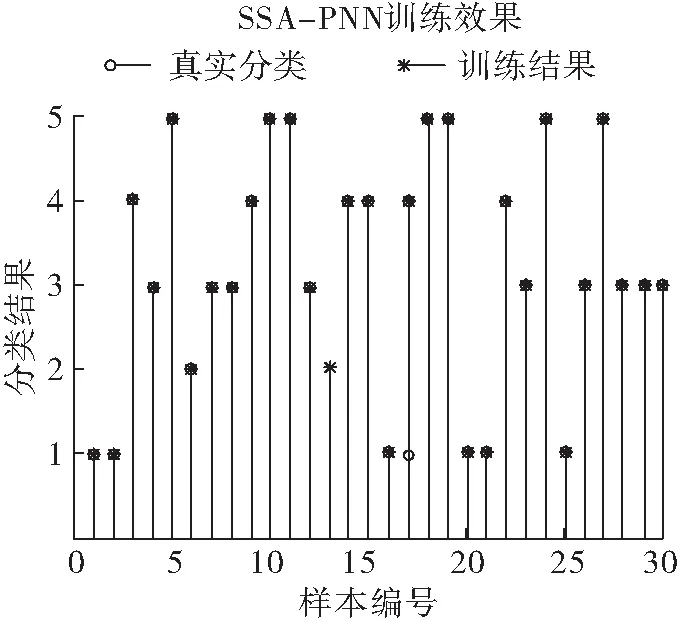
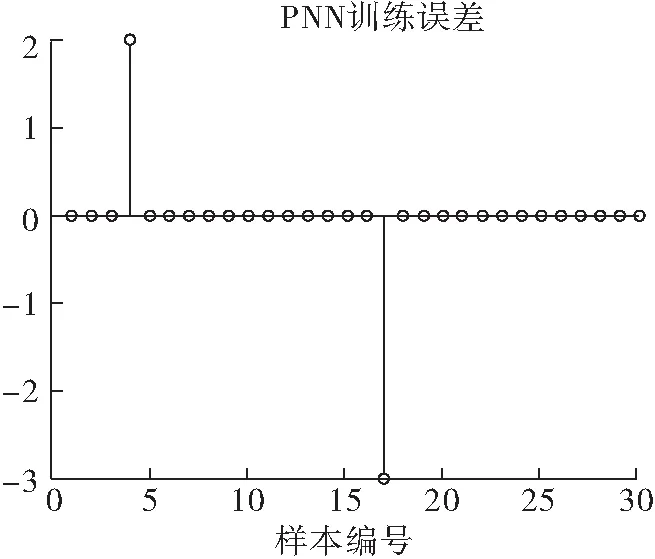
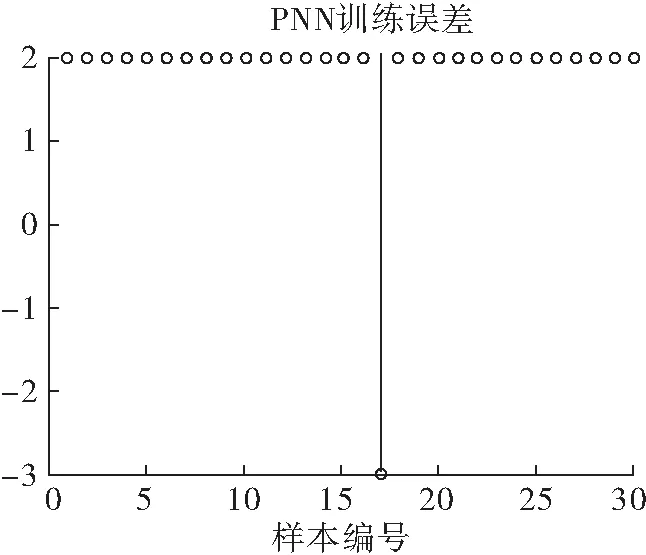
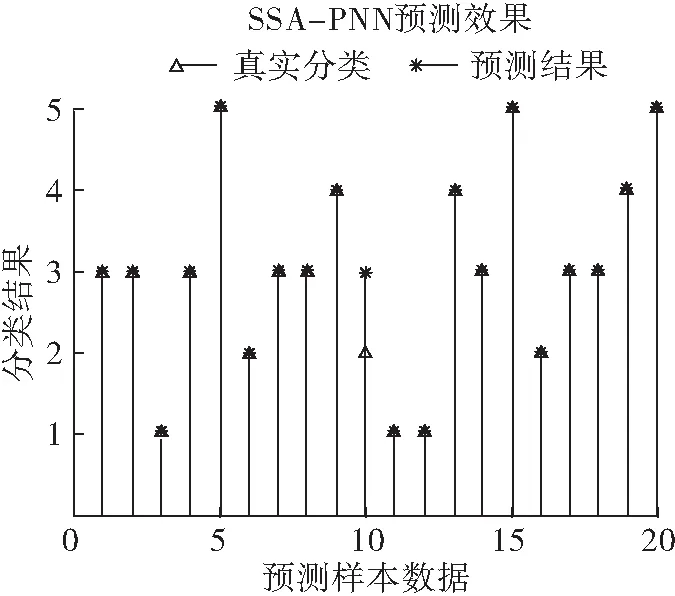
式中:t为种群目前的迭代次数;itermax为整个群体最大迭代次数;Xti,j表示在第t代迭代过程中,第i只麻雀第j维的信息;0 (5) 式中:XP为当前发现者所处于的最佳位置;Xworst为目前群体中的最劣位置;A是一个1×d的矩阵,矩阵元素为1或-1,其取值具有随机性,且满足A+=AT(AAT)-1,A+是一个伪逆矩阵,当i>n/2时表示第i只麻雀此时健康值较低,没有获取食物,需要到其他地方探索以获取食物以提高自身适应度。 通常情况下发现危险的麻雀占麻雀群体数量的10%~20%,当危险来临时,麻雀的位置更新公式为: (6) 在变压器故障诊断中,传统的PNN网络模型首先收集并处理数据,接下来利用训练集训练PNN网络,最后利用测试数据检测模型的泛化程度,为了解决PNN网络平滑因子设定的不确定性问题,建立SSA-PNN变压器故障诊断模型,选取最佳的平滑因子。 SSA优化PNN的变压器故障诊断流程图如图2所示。 图2 SSA优化PNN流程图 (1)在改良三比值法的基础上确定故障诊断模型的输入输出,输入端以油中溶解气体含量的三对比值(CH4/H2,C2H2/C2H4和C2H4/C2H6)作为样本特征向量[15]。输出端以变压器的不同故障类型作为输出向量,并建立相应的训练样本集和测试样本集。 (2)初始化SSA参数,设置种群规模,意识到危险的麻雀数量,最大迭代次数等。 (3)利用麻雀搜索算法对PNN网络的平滑因子进行优化。适应度函数设计为训练集与测试集的分类错误率。 (4)通过公式(4)~(6)更新麻雀种群中发现者、加入者、发现危险的麻雀位置,并计算相应位置的适应度值,更新全局最优信息。 (5)迭代直到最大迭代次数,输出全局最优参数,将测试集样本数据输入至最优PNN网络,输出变压器故障诊断结果。 结合西北某地1#主变压器实际运行中采集的油中溶解气体故障数据,提取其中的50组数据构成50×4维的矩阵,前三列数据为改良三比值法处理后的数值,最后一列为变压器故障类型,前30组数据用作训练集,后20组数据作为测试集。改良三比值法对应的故障类型如表1所示,处理后的前8组数据如表2所示[16-17]。 表1 改良三比值法故障类型判断方法 表2 前8组油中溶解气体比值 SSA-PNN参数设置如下:麻雀种群规模POP设置为20,发现者的比例PD设置为0.7,意识到危险的麻雀比例SD设置为0.2,最大迭代次数设置itermax为20,安全阈值ST设置为0.2,输入层神经元个数为3,样本层神经元个数设置为30,求和层神经元个数设置3。将训练集样本数据分别带入PNN网络和SSA-PNN网络,则网络训练后的效果如图3和图4所示。 图3 PNN网络训练效果 图4 SSA-PNN训练效果 通过对比分析仿真结果可知,将前30组数据分别带入训练好的PNN网络和SSA-PNN网络,PNN网络有两个样本分类出现错误,SSA-PNN网络只有一个样本分类出现错误,分类正确率分别为93.3%和96.6%,两种网络的分类误差图如图5和图6所示。 图5 PNN训练误差 图6 SSA- PNN训练误差 训练后的SSA-PNN网络Fitness为0.083 3,Spread为0.814 0,PNN网络Spread设置为1.5,为了进一步对比验证SSA-PNN网络的变压器故障诊断能力,将测试集20组数据分别带入训练好的SSA-PNN网络和PNN网络,其故障分类预测结果如图7和图8所示。 图7 PNN预测结果 图8 SSA-PNN预测结果 由仿真结果可知,PNN故障预测准确率为85%,错误预测样本数为3,SSA-PNN故障预测准确率为95%,错误预测样本数为1,相对于PNN网络,SSA-PNN网络在变压器故障分类预测准确率上有明显提升,且方法可行度较高,对于变压器故障的快速诊断和判别具有较强的工程实际意义。 该文采用SSA算法对PNN网络平滑因子参数σ进行优化,从仿真结果可以看出,相对于基础PNN网络,改进后的SSA-PNN网络在变压器故障诊断正确率上有明显的提升。另一方面,PNN网络样本层神经元的数量取决于实际样本数量,但在实际应用中,训练样本数量往往较多,所需的样本层神经元的数量也会大幅增加,这将极大地耗费计算机的数据处理能力,在一定程度上限制了PNN网络的实际应用和推广。下一步,将通过对样本层神经元数量进行优化,使PNN网络更加完善。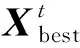
2 SSA优化PNN故障诊断流程

3 算例分析


4 结论
