基于油气弹簧的六臂结构轮对式悬挂分析

冯伟琦，武志博，焦 斌，马铁华

(中北大学 a.电子测试技术重点实验室； b.电气与控制工程学院， 太原 030051)

1 引言

重载车辆轮对式驱动模式拥有比传统车辆优越的机动性，减少动力传递中的损耗，实现单轮独立的转速与转矩控制，但是传统悬挂仅具有垂直方向的单一自由度，设计研究适用于轮毂电机轮对驱动模式的多自由度悬挂装置是当前车辆悬挂领域的一个重要研究热点。本研究以油气弹簧为基础分析一种六臂油气弹簧结构悬挂设计的可行性。油气弹簧由于非线性气体特性使得悬挂刚度随负载发生变化，相比传统被动悬挂能够更好地适应不同路况。目前由于油气弹簧结构相对于传统悬挂复杂生产成本更高，因此并未在普通车辆广泛应用，但是油气弹簧的非线性变刚度和刚度渐增(减)特性及单位储能比大、结构紧凑、参数调整方便、适应负载变化能力强等优点却满足了一部分特种车辆(军工特种车辆、消防车辆等)高性能的要求。油气弹簧良好的非线性特性给车辆性能带来提升的过程中，也由于非线性特性给设计工作带来重复性和不确定性，因此，为了提高油气弹簧在重载车辆的应用范围以及提高重载车辆的悬挂性能减少不必要的重复性试验提高悬挂的设计效率，进行相应的数学建模分析是十分必要的。

2 轮毂电机轮对式模块化驱动设计

随着电机技术的发展，将电机集成至车辆轮毂中作为独立的驱动单元，相比于传统驱动方式需要发动机与传动机构轮毂电机车轮具有结构简单分布驱动的特点。同时传统车辆转向方式依然依靠转向拉杆等机构，而电机控制技术的飞速发展使得利用轮对差速控制转向成为可能，如常见的平衡车，但若要将轮毂电机轮对式驱动模式利用在大载荷的工程应用中必须设计可靠合理的悬挂机构。如图1(a)、(b)所示为轮毂电机轮对式结构示意图。

图1 轮毂电机轮对式结构示意图

独立单元的轮毂电机轮对式模块化驱动对悬挂设计提出了新的要求即悬挂机构也应具有单元化模块化的特点，这就要求单元化的悬挂模块具有承受各向载荷的能力，而非传统的悬挂只具有承受垂直载荷的能力，纵向载荷与横向载荷依赖车架或承载式车身刚性抵抗冲击。同时高灵活性与通过性对悬挂的结构设计同样提出要求。故此基于油气弹簧的六臂结构悬挂可满足以上要求，具体为外四臂与内二臂的组合结构，如图2为六臂悬挂结构示意图。

图2 六臂悬挂示意图

基于油气弹簧六臂结构悬挂将自由度由传统的2自由度放开至6自由度，首先具有承受各向载荷的特点，同时提高了轮对的机动性和灵活性，但却存在轮对差速转向过程中存在不稳定以及轮毂电机车轮导致的簧下质量过高的缺点。在辅以拉伸弹簧的作用下，不仅可有效改善轮对差速转向的不稳定问题，同时拉伸弹簧的作用等效降低了簧下质量提高了悬挂响应速度，而且拉伸弹簧对抵抗横向载荷与纵向载荷也具有辅助作用。图3为拉伸弹簧示意图。

图3 拉伸弹簧示意图

综上基于油气弹簧的六臂结构悬挂结合拉伸弹簧作用下，具有以下特点：

1) 承受纵向载荷：刹车、加速等情况下的纵向载荷通过相应的油气弹簧与拉伸弹簧抵抗并通过阻尼孔卸掉冲击，如图4(a)所示。

2) 承受横向载荷：转弯、侧倾等情况下的横向载荷通过相应的油气弹簧与拉伸弹簧抵抗并通过阻尼孔卸掉冲击，如图4(b)所示。

3) 承受垂直载荷：路面不平整等情况下的和垂直载荷在油气弹簧与拉伸弹簧作用下快速响应，如图4(c)所示。

4) 水平转向：轮对差速转向过程中，油气弹簧随之扭转产生扰动扭转的扭矩，在拉伸弹簧的矫正作用下，具有抵抗扰动力矩的能力，如图4(d)所示。

图4 不同情况下轮对受力示意图

通过上述定性分析六臂结构的轮对式悬挂在辅以拉伸弹簧的作用下，具有承受各项载荷的能力，同时在垂直载荷上拉伸弹簧具有降低簧下质量提高悬挂响应的优点，但转向过程存在的不稳定性问题还需定量研究。

3 油气弹簧数学建模

为适应六臂结构的油气弹簧结构采用单气室油气弹簧结构简单、体积小。单气室油气弹簧结构如图5所示，活塞杆上下运动的过程中液压油通过阻尼孔在内油室和外油室之间往复运动，压缩气室内的高压氮气达到减振作用。

图5 油气弹簧结构示意图

图5中，对应活塞杆氮气腔，对应活塞杆内油室，对应活塞杆外油室。代表氮气腔有效作用面积，代表内油室有效作用面积，代表外油室有效作用面积。则

(1)

(2)

当活塞杆处于静平衡状态时，静平衡力方程为

0·=·=·

(3)

当活塞杆发生运动时，氮气腔与内外两油室的容积变化量为

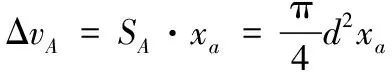
(4)

(5)

(6)

当油气弹簧活塞杆发生相对位移时，其内外油室中的体积变化如下：

Δ=Δ

(7)

(8)

根据体积变化可求得无杆活塞运动位移为

(9)

将氮气腔内的气体看作理想气体，根据理想状态方程有

(10)

由此可得出

(11)

整理得

(12)

综上油气弹簧的负载与位移的关系，即单气室油气弹簧的弹性力方程为

(13)

式中：为氮气腔有效作用面积；为内油室有效作用面积；为外油室有效作用面积；为外缸体内径；为活塞杆内径；0为氮气腔初始气压；为内油室初始油压；为外油室初始油压；Δ为活塞杆内氮气腔容积变化量；Δ为活塞杆内油室容积变化量；Δ为活塞杆外油室容积变化量；为浮动活塞运动位移；为氮气腔初始气体体积；为活塞杆发生位移时对应氮气气腔气压；为活塞发生位移时对应氮气腔体积；为气体多变指数。

表1 油气弹簧初始参数

代入表1中的油气弹簧的初始参数到模型中，得到图6油气弹簧的位移负载曲线。

4 水平旋转稳定分析

六臂油气弹簧结构悬挂装置在水平旋转过程中，由于六臂油气弹簧的伸缩程度各不相同会产生旋转扭矩对于影响悬挂的稳定性，因此分析计算在辅以拉伸弹簧的作用下水平旋转方向的稳定性必不可少。如图7所示为水平旋转示意图其中、、、、、为油气弹簧上端与车体连接球头，、、、、为油气弹簧下端与轮对连接球头，为水平旋转中心，′′′′为4个角油气弹簧下端旋转之后的球头位置。

图6 油气弹簧的位移负载曲线

图7 水平旋转示意图

4.1 油气弹簧位移负载变化分析

如图8所示，规定逆时针方向为正方向，由图7可知在水平旋转过程中油气弹簧位移负载上下对称，因此分析上方3根油气弹簧的位移负载变化。由图8可知旋转过程中即中间油气弹簧不会产生影响悬挂稳定性的旋转扭矩，而左右两根油气弹簧会产生影响悬挂稳定性的旋转扭矩，假设轮对逆时针旋转角度，其中为油气弹簧上下球头垂直距离；为油气弹簧初始长度为；为下球角与旋转中心的距离；为上球角与旋转中心的水平投影距离。

图8 上方3根油气弹簧水平旋转简化模型示意图

4.1.1 左侧油气弹簧位移负载变化分析

静平衡位置处左侧油气弹簧上下球角水平距离

(14)

静平衡位置处油气弹簧下端球头与旋转中心连线和上端球头与旋转中心连接线夹角

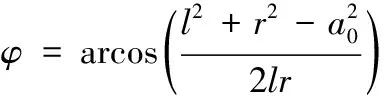
(15)

旋转后，油气弹簧水平投影长度

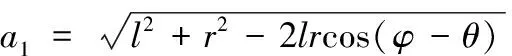
(16)

则变化后的油气弹簧长度

(17)

左侧油气弹簧对应的旋转力臂为

(18)

=sin

(19)

联立式(14)～式(19)得到旋转角后，左侧油气弹簧力负载为

(20)

则左侧油气弹簧提供的不稳定旋转扭矩为

(21)

412 右侧油气弹簧位移负载变化分析

静平衡位置处右侧油气弹簧上下球角水平距离为

(22)

静平衡位置处油气弹簧下端球头与旋转中心连线和上端球头与旋转中心连接线夹角为

(23)

旋转后，油气弹簧水平投影长度为

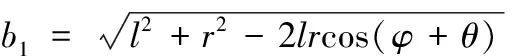
(24)

则变化后的油气弹簧长度为

(25)

右侧油气弹簧对应的旋转力臂为

(26)

=sin

(27)

联立式(22)～式(27)得到旋转角后，右侧油气弹簧力负载为

(28)

则右侧油气弹簧提供的不稳定旋转扭矩为

(29)

联立式(21)和式(29)随着水平旋转角度的变化，不稳定旋转扭矩为

(30)

将表2中的初始参数输入到模型中，得到图9所示的液压杆力随旋转角度变化曲线，图10为旋转液压杆伸缩变化量随旋转角度变化量曲线，图11为旋转力矩、抵抗力矩、合力矩随旋转角度变化曲线。

表2 悬挂初始参数

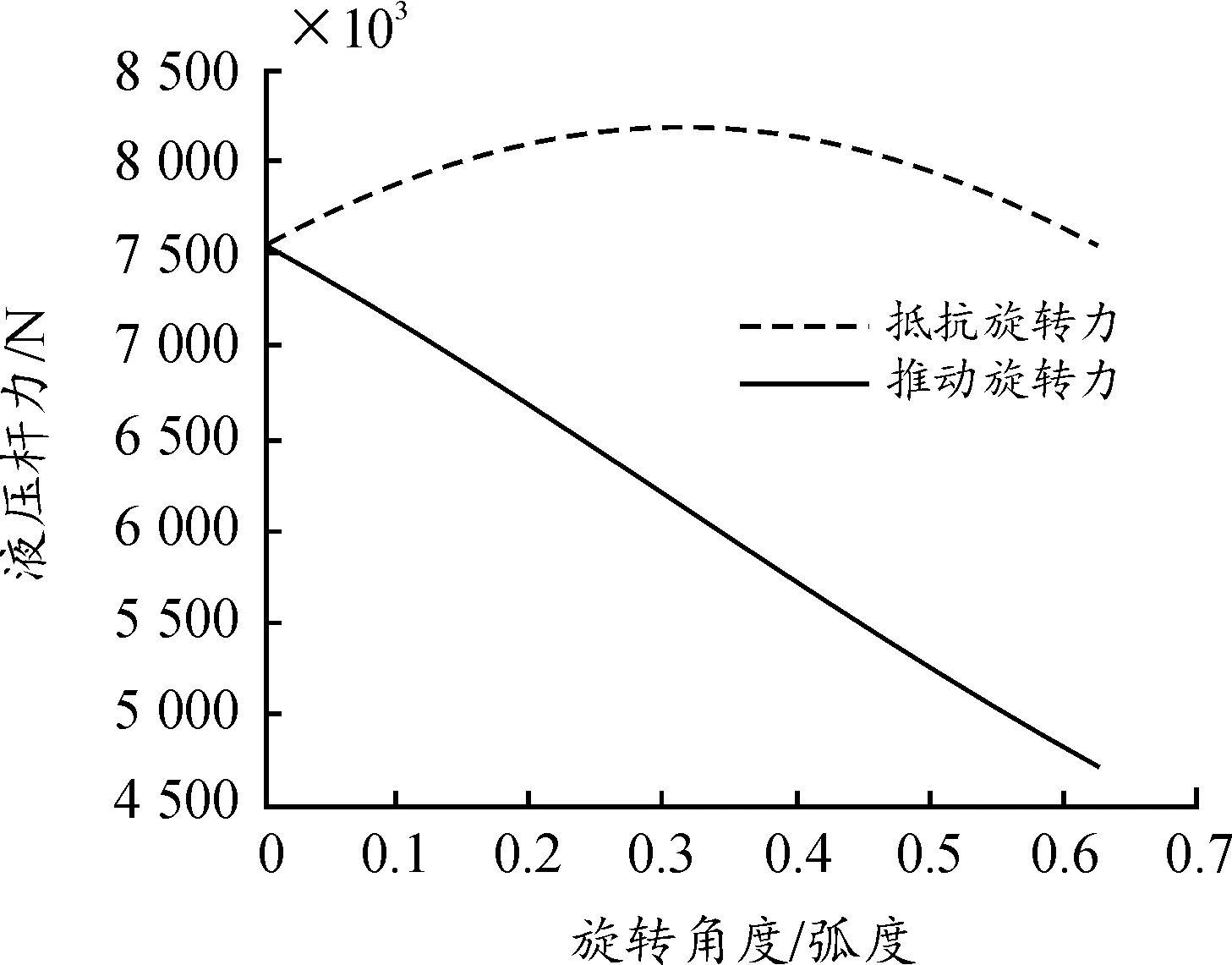
图9 液压杆力随旋转角度变化曲线

图10 旋转液压杆伸缩变化量随旋转角度变化曲线

图11 旋转力矩、抵抗力矩、合力矩随旋转角度变化曲线

根据图11可以得出在不辅以弹簧作用下，六臂油气弹簧结构随水平旋转发生变化即偏离初始位置后，由于六臂油气弹簧的非线性刚度特性，在逆时针旋转的过程中，左侧油气弹簧虽然旋转力臂一直在减小，但是弹性力增加的更快，最终结果是在一定范围内，逆时针旋转的过程中有抵抗旋转的扭矩即六臂油气弹簧具有较强的自稳状态。

4.2 弹簧矫正力分析

如图12所示，4根拉伸弹簧固定端安装在与4个角上油气弹簧上端球头垂直的车体下方，活动端安装在油气弹簧下端球头固定处。故而弹簧受力水平投影分析图与图8一致，但弹簧初始长度及上下两端的垂直距离与油气弹簧不同，规定弹簧初始长度为，弹簧上下两端垂直距离为。

图12 弹簧受力水平投影分析示意图

弹簧刚度计算公式为

(31)

其中：为弹簧材料的剪切模量；为弹簧丝径；为弹簧中径；为弹簧有效圈数。

421 左侧拉伸弹簧位移拉力变化

静平衡位置处左侧拉伸弹簧上下固定端水平距离为

(32)

静平衡位置处拉伸弹簧下固定端与旋转中心连线和上固定端与旋转中心连接线夹角为

(33)

旋转后，拉伸弹簧水平面投影长度为

(34)

则变化后的拉伸弹簧长度为

(35)

左侧油气弹簧对应的旋转力臂为

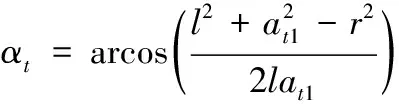
(36)

1=sin

(37)

联立式(32)～式(37)得到旋转角后，左侧拉伸弹簧拉伸力为

(38)

则左侧油气弹簧提供的不稳定旋转扭矩为

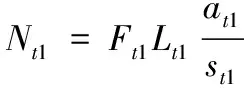
(39)

422 右侧拉伸弹簧位移拉力变化

静平衡位置处右侧拉伸弹簧上下球角水平距离为

(40)

静平衡位置处拉右侧伸弹簧下固定端与旋转中心连线和上端球头与旋转中心连接线夹角为

(41)

旋转后，右侧拉伸弹簧水平投影长度为

(42)

则变化后的右侧拉伸弹簧长度为

(43)

右侧拉伸弹簧对应的旋转力臂为

(44)

2=sin

(45)

联立式(40)～式(45)得到旋转角后，右侧拉伸弹簧拉力为

(46)

则右侧拉伸弹簧提供的矫正旋转扭矩为

(47)

联立式(39)和式(47)随着水平旋转角度的变化，弹簧矫正扭矩为

(48)

4.3 轮对水平旋转扭矩分析

在六臂油气弹簧悬挂结构中辅以拉伸弹簧，轮对最终受到的旋转扭矩为

=+=2(+)+2(1+2)=

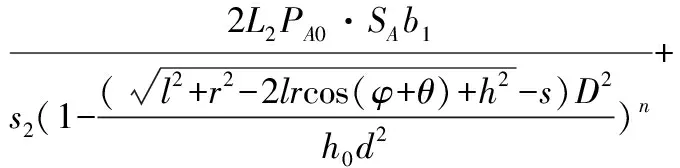
将拉伸弹簧参数(如表3所示)代入到模型中，最终可以得到图13油气弹簧旋转力矩、拉伸抵抗力矩、合力矩随旋转角度变化曲线。

由图13结果表明，六臂油气弹簧结构悬挂装置在水平旋转过程中，由于油气弹簧伸缩程度各不相同而产生的旋转扭矩，在油气弹簧旋转力矩和拉伸弹簧抵抗力矩的共同作用下，轮对受到的合力矩基本维持在0 N·m。

表3 拉伸弹簧参数

图13 油气弹簧旋转力矩、拉伸抵抗力矩、合力矩 随旋转角度变化曲线

4.4 弹簧一致性分析及刚度校准

由于工业生产过程中生产工艺的限制会导致弹簧的丝径、外径以及材料的应力等误差，间接导致弹簧的刚度误差即多组弹簧的不一致性问题。弹簧的不一致性会对六臂结构轮对式悬挂装置的矫正产生与理论计算不适应的问题。通过在弹簧与悬挂机构安装处设计调节机构进行系统性校准将弹簧不一致性降到最低；同时通过左右车轮与地面摩擦力的不同而产生的扭矩动态弥补由于弹簧不一致性导致的非零矫正扭。

在弹簧与模块化轮腿定子连接处设置有可对弹簧初始长度微调的机构，通过对弹簧长度的微调尽可能将弹簧刚度调整为与理论值相同。

以弹簧刚度误差±5%作为计算最大误差进行仿真计算，当分别沿对角线的两组弹簧，一组为+5%，一组为-5%时，产生的矫正扭矩误差最大，进行计算后仿真结果如图14，仿真结果表明，在弹簧刚度±5%误差情况下，弹簧矫正作用会产生抵抗旋转/助推旋转的扭矩，扭矩大小为约±50 N·m，对于轮对式驱动模式，依靠左右车轮动态调节弥补小于50 N·m的力矩仍具有可实现性与实用性。

图14 弹簧不一致情况下各力矩随旋转角度变化曲线

5 结论

随着新型驱动模式不断发展，提出了一种模块化轮对驱动模式，即驱动与悬挂装置一体的驱动模式，并针对此驱动模式设计了一种基于油气弹簧的六臂结构轮对式悬挂装置。对其进行静力学分析，在轮对转向即水平旋转过程中，由于气体的非线性刚度特性，虽然推动旋转的油气弹簧旋转力臂随旋转角增大而阻碍旋转的油气弹簧旋转力臂随旋转角减小，但是阻碍旋转的油气弹簧负载力呈指数增加，使得在一定范围内悬挂结构具有较强的自稳定结构，但同时此结构会严重的影响轮对的差速转向过程，带来极大的负面作用。在辅以拉伸弹簧的作用下，油气弹簧的旋转力矩与拉伸弹簧的拉伸抵抗力矩相互抵消，轮对所受到合力矩基本维持在0 N·m，同时考虑弹簧在加工过程中存在的不一致性，利用调节机构对弹簧不一致性进行校准将弹簧刚度误差保持在±5%内得到最大误差扭矩约50 N·m，依赖轮对差速的动态调节以弥补弹簧的不一致性，依然可达到理想的稳定效果与转向条件。