子母式发烟弹全弹道建模与分析
2022-02-21李红欣盖希强张开创
陈 浩,李红欣,盖希强,赵 新,张开创,杨 洋
(1.军事科学院防化研究院, 北京 102205; 陆军装备部驻北京地区军事代表局, 北京 100071)
1 引言
抛撒技术作为子母弹的核心技术之一,是世界各军事强国研究的重点。围绕子母弹的抛撒过程,国内外学者开展了大量研究。Stalmach等针对子弹旋转分离与抛撒方式等空气动力学问题,在超音速风洞中开展了相关实验的研究与分析,根据确定的气动参数,对子母弹气动外形进行了优化设计。Panneerselvam等建立了风洞实验模型,研究了子弹在不同攻角条件和处于母弹不同位置条件下气动参数的变化规律。通过建立6自由度弹道模型,进一步分析了子母战斗部的弹道特性。蒋建伟等根据格尼公式,建立了包括抛撒速度、自由飞行和落点散布的模型,为工程应用提供了理论指导。孙新利等针对高燃速抛射火药,建立了子弹抛射理论模型,计算了子弹抛射初速,设计了子母弹装置,在实验室条件下,利用高速摄影记录开舱与子弹抛射过程,通过图像处理得到了不同药量下的子弹速度、位移等数据,验证了模型的正确性。郭锦炎等为使子弹在低过载环境下获取较高的抛撒速度,设计了一种活塞式中心抛撒机构,通过建立内弹道模型,计算得到抛撒机构可为子弹提供大于50 m/s的抛撒速度,并控制子弹过载在1 000 g以内。郝辉等通过建立抛撒模型和子弹弹道模型,对引起子母弹抛撒参数偏差的6种因素进行了分析,为子弹散布研究提供了参考。刘静敏针对大口径中心爆管式子母弹抛撒机构的工作原理进行了分析,设计了抛撒机构,通过有限元软件将流体方程与子弹六自由度运动方程耦合在一起,对子母弹分离流场进行了模拟,得到了初始扰动、弹体尺寸参数等对子母弹分离的影响规律,对抛撒机构设计提供了指导。祁少文利用抛撒药燃烧方程、子弹运动方程、能量守恒方程等建立方程组,对子弹过载进行了求解,利用动态测试理论的方法,设计了一套测试系统,对子弹抛撒过程中过载情况进行了模拟,为子母弹战斗部研制与改进提供了很好的依据。李东光等针对高速旋转子母弹定时开舱子弹散布精度低的问题,通过建立子弹全弹道模型,分析了初速、射角、抛撒高度误差的影响,提出基于开舱高度修正的母弹自适应技术来提高子弹落点精度。王金龙等针对子母弹燃气囊抛撒试验中气囊破裂对子弹运动特性的影响,利用Fluent软件建立气囊抛撒三维有限元模型,通过获取不同破口位置气囊内压力变化规律,得到中间位置发生破裂对子弹姿态影响较大,对研究提高子母弹分离的可靠性提供重要参考。
上述文献针对不同类型的子母弹战斗部抛撒与分离过程模型建立、装置设计、抛撒点特征参数影响因素分析等方面进行了创新与改进,但对于大口径平台的子母式特种弹药,由于战斗部壳体较厚,常采用后抛的抛撒模式,全弹道模型的建立、计算与分析过程更复杂,中间开舱式子母弹的抛撒技术并不能完全适用。
基于大口径子母式发烟弹,建立子母式发烟弹的母弹飞行弹道、子弹抛撒内弹道和子弹飞行弹道,采用Matlab软件,分析计算母弹飞行弹道、子弹抛撒内弹道的弹道诸元变化规律,确定子弹抛撒高度、抛撒时间、抛撒点特征点参数;基于横向间隔距离,建立目标函数,分析计算子弹的阻力系数及子弹飞行弹道的弹道诸元变化规律。通过开展子弹静爆试验,验证子弹间隔的合理性及全弹道抛撒方案的正确性。
2 发烟弹全弹道建模
根据子母式发烟弹的弹道特征,将其飞行弹道分为3个阶段,即母弹飞行弹道阶段、子弹抛撒内弹道阶段和子弹飞行弹道阶段,如图1所示。

图1 多频谱干扰弹全弹道示意图
2.1 母弹飞行弹道模型建立
根据经典力学,任意刚体在空间运动,可分解为随质心的平移和绕质心的转动。根据牛顿第二定律,将干扰弹视为刚体,在发射惯性系建立其质心动力学方程为:
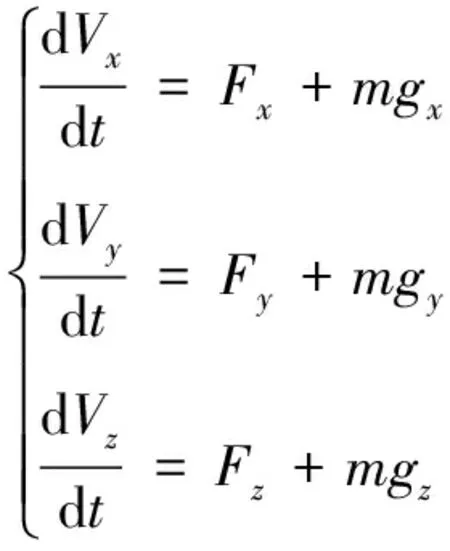
(1)
式(1)中:、、为弹丸在发射惯性系下的位置(m);、、为弹丸在发射惯性系下的速度(m/s);、、为弹丸受到的气动力在发射惯性系下各坐标轴上的分(N);、、为重力加速度在发射惯性系下各坐标轴上的分量(m/s)。
弹丸在发射惯性系内的质心运动学方程为:
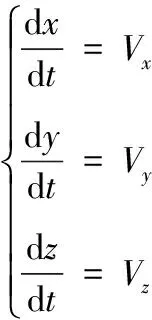
(2)
根据动量矩定理,弹丸相对于质心的动量矩等于所受到的合外力矩,则在准弹体系建立绕心运动的动力学方程为:

(3)
在准弹体系建立绕心运动的运动学方程为:

(4)
2.2 子弹抛撒内弹道模型建立
子弹抛撒与分离过程会影响烟幕遮蔽的连续性和分散性,因此,为进一步建立抛撒与分离过程模型,通常规定:
1) 子弹能够承受抛撒药过载。
2) 子弹尽可能提高抛射速度,从而减小子弹的存速及设计难度。
3) 子弹在抛撒与分离过程中,要避免相互碰撞,防止子弹弹道性能下降,影响烟幕成形与遮蔽。
4) 子弹分开一定横向间隔距离,保证爆炸分散形成的烟幕面积大小最优。
干扰弹到达预定位置后,引信作用,使抛撒药燃爆,并产生大量高温高压气体使得弹体空间压力急剧增大。当达到启动压力后,弹底被剪断,火药燃气推动子弹后抛。将子弹看作弹丸,则子弹抛撒过程可看作内弹道过程,从抛撒药点燃到罐体被抛射出弹底位置,此过程与经典内弹道过程基本一致,选用黑火药作为抛撒药,根据经典内弹道理论,得到抛撒药的燃速模型和抛撒药的已燃百分数的表达式为:
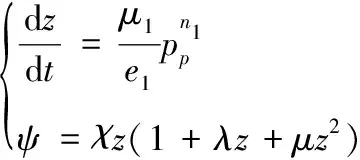
(5)
式(5)中:为抛撒药的相对燃烧厚度,即=,其中,为已经燃烧厚度的12(mm),为初始厚度的12(mm);为抛撒药的燃速系数;为抛撒药的压力系数;为抛射压力(Pa)。
以抛撒点作为惯性坐标系的坐标原点,向右为正、向左为负,惯性坐标系相对大地坐标系以开舱点弹体速度运动。在子弹抛射过程中,近似认为子弹与干扰弹弹体满足动量守恒定理,经整理得到抛撒过程的弹道方程组为:

(6)
式(6)中:为弹体内腔的横截面积(m);为子弹的质量(kg);为干扰弹弹体的质量(kg);为惯性坐标系下子弹的位移(m);为惯性坐标系下干扰弹弹体的位移(m);为子弹的抛射速度(m/s);为干扰弹弹体抛射速度(m/s);为子弹次要功系数;为弹体次要功系数;为药室自由容积缩径长(m);为药室容积缩径比(m);为抛撒药的火药力(J/kg);为抛撒药热力参数;为抛撒药的密度(kg/m);为抛撒药的余容。
2.3 子弹飞行弹道模型建立
子弹经火药燃气作用,相对干扰弹弹体抛出弹底后,罐体翼片张开,使各罐体稳定姿态。如图2所示,从弹底到干扰弹头部方向上依次装填着子弹3、子弹2和子弹1。在子弹1上加装4片翼片,在子弹2上加装2片翼片,在子弹3上不加装翼片。

图2 子弹分离过程的示意图
由于各罐体翼片的不同,使得各自承受的气动阻力各不相同。飞行预定时间后,当罐体间分离的横向距离与单个罐体爆炸形成的初始云团的烟幕宽度一致时,罐体内部的延时装置作用,罐体爆炸形成连续的烟幕云团,如图3所示。根据第4节烟幕初始云团1 s时的膨胀半径的计算与试验结果,子弹起爆后1 s,烟幕初始云团为6 m宽度。因此,以烟幕初始云团宽度作为子弹横向间隔距离,满足快速成烟的实战需求,且各子弹形成的烟幕可连成一片,能对目标实现有效遮蔽。基于以上原因,将烟幕初始云团6 m烟宽作为子弹最佳横向间隔距离,用于后续计算与分析。
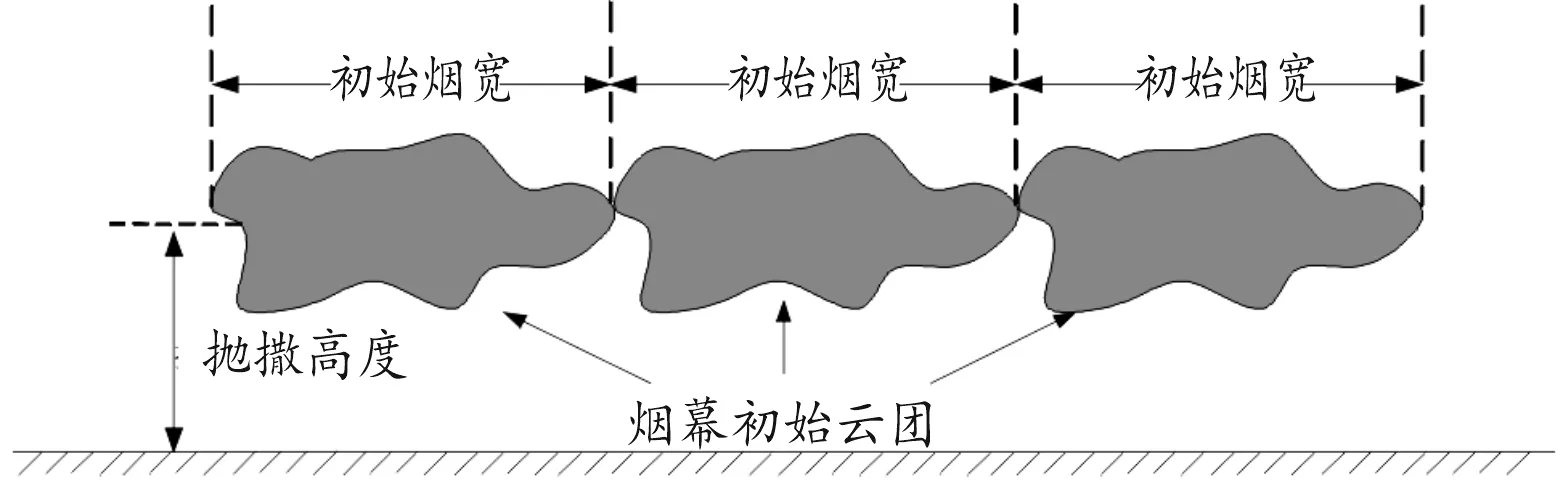
图3 子弹最佳分散效果示意图
上述对子弹分离过程进行了分析,为确定第1组射击条件和第2组射击条件下干扰弹的抛撒策略,下一步将建立子弹分离过程的弹道模型,分析与研究分离过程横向运动距离、时间等参数。
为建立子弹的分离过程模型,假设如下:
1) 各个子弹在此飞行阶段的阻力系数为常数。
2) 子弹被抛出弹体后无扰动,即子弹初始弹道倾角与母弹抛射过程的弹道倾角保持一致。
3) 子弹被抛出后,将其看做质点。
基于以上假设,根据质点弹道理论,可得子弹运动方程为:

(7)
式(7)中:为弹道系数,它等于×10m,为弹形系数;()为空气密度函数;为马赫数,是弹丸速度与声速的比值;0为标准弹的阻力系数。
3 全弹道模型数值计算
3.1 母弹飞行弹道计算
根据弹道射击实际情况,选取最小射程这一极限状态,进行计算。3发子弹药各装填2 kg多频谱发烟剂,发烟弹弹重45.5 kg,战斗部设计参数与杀爆战斗部保持一致性。在标准气象条件下,主要初值如表1所示。

表1 仿真主要初值
采用4阶龙格-库塔法,最小射程条件下发烟弹6自由度外弹道模型进行数值计算,基于烟幕作战需求,发烟弹的各子弹的最佳起爆高度定为10 m,以此作为约束条件,计算得到位置、速度和弹道倾角变化规律如图4~图7所示。

图4 距离x随时间变化曲线

图5 弹道高度y随时间变化曲线

图6 速度v随时间变化曲线
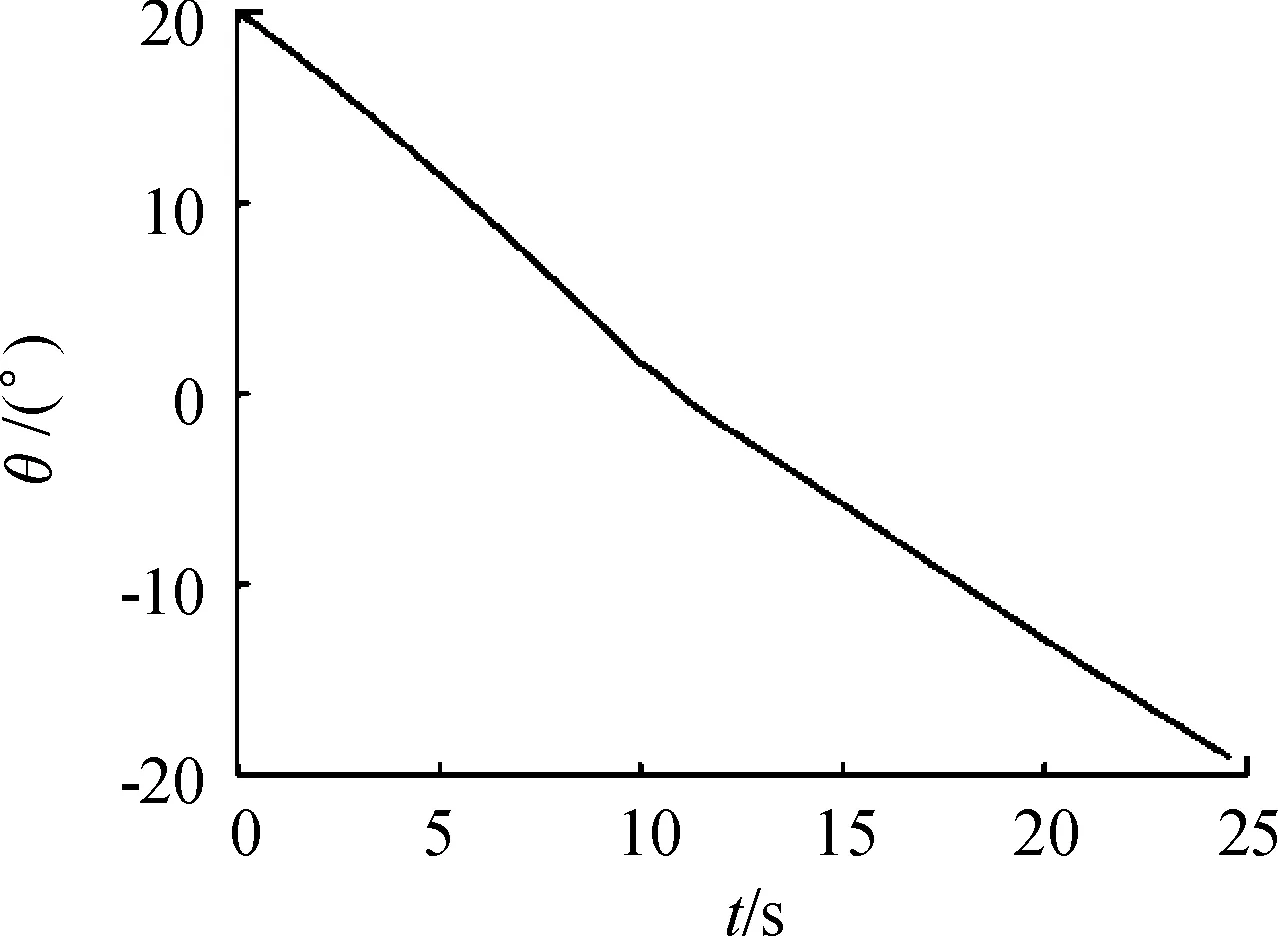
图7 弹道倾角θ随时间变化曲线
在最小射程条件下,基于Matlab计算得到发烟弹飞行弹道的各诸元变化。根据图4~图6可知,发烟弹在全弹道过程中,、方向的速度分量与阻力方向一致相反,速度持续降低;在过弹道顶点前,方向速度分量与重力加速度分量方向相反,方向速度降低;过弹道顶点后,方向速度分量与重力加速度分量方向一致,方向速度升高。当方向速度增量与、方向的速度减量抵消,此时,干扰弹速度达到最小值,因此,干扰弹速度在全弹道过程中呈现先降低后增加,最小值点出现在降弧段。弹道高度达到500 m后,随时间的推移,弹丸水平速度在240~260 m/s,剩余时间小于8 s。基于子母式干扰弹的设计原理及试验经验,在各子弹上加装不同阻力系数的翼片,速度差为5~10 m/s,基于子弹的横向间隔,罐体均匀分散所需时间约为1~2 s。基于以上条件及子弹抛撒与分散的需求,以子弹到达10 m起爆高度的剩余时间2 s为另一约束条件,确定了干扰弹抛撒点的相关弹道诸元,如表2所示。

表2 最小射程条件下抛撒点相关弹道诸元
3.2 子弹抛撒过程计算
抛撒药选用HY-5黑火药,采用四阶龙格-库塔法对抛撒内弹道运动过程进行求解,计算结果如图8~图10所示。
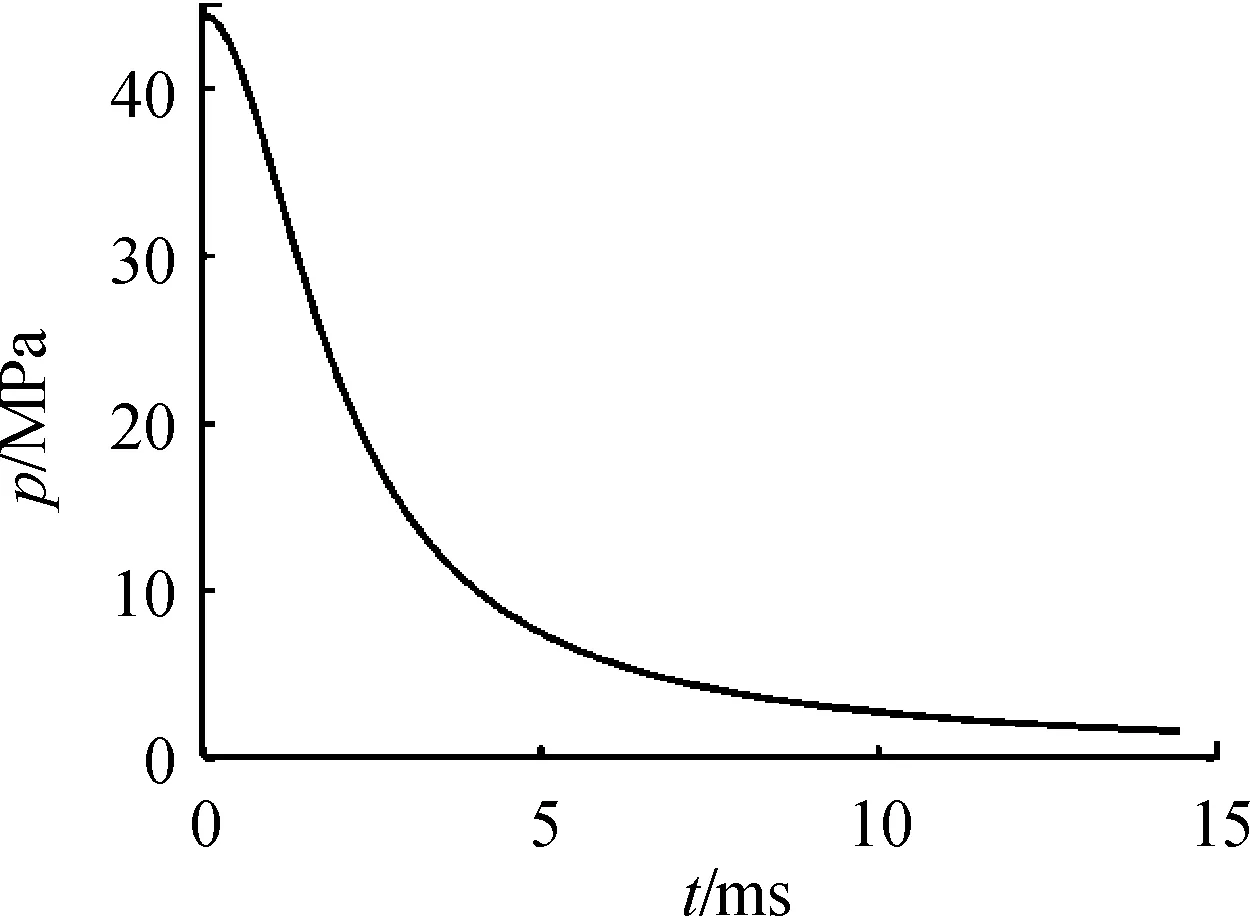
图8 抛射压力随时间的变化曲线

图9 子弹抛射速度随时间的变化曲线

图10 弹体抛射速度随时间的变化曲线
由图8~图10可知,在惯性坐标系内,子弹被抛出弹体的时间为14.4 ms,抛撒结束后,子弹的抛射速度为39.9 m/s,方向与定义的惯性坐标系正方向相反;干扰弹弹体的抛射速度为3.8 m/s,与定义的惯性坐标系正方向一致。
3.3 子弹抛撒内弹道计算
基于干扰弹6自由度刚体弹道模型及子弹抛撒过程内弹道模型,计算得到的抛撒点速度、弹道倾角及高度作为子弹分离过程模型的初始参数,如表3所示。

表3 子弹分离过程模型的初始参数一览表
为有效计算子弹分离过程模型并基于最佳子弹间隔求解各子弹的阻力系数,还需采用各子弹自身的阻力系数取代标准阻力系数0。根据子弹尺寸和外形,采用DATCOM工程计算软件,计算得到射击条件,不加装阻力翼片的子弹3的阻力系数为0.019。
当子弹2和子弹1加装阻力翼片后,二者的阻力系数增加。以子弹3的阻力系数为变量,基于上述分析,以第4节得到的烟幕初始云团1 s时刻烟幕宽度6 m,作为子弹的最佳横向间隔,并以此作为目标函数。以子弹3作为基础弹道,计算弹道高为10 m时,子弹2和子弹1在不同阻力系数下横向间隔距离差的计算公式为:
Δ=|--6|
(8)
式(8)中:和分别为子弹1和子弹2的横向运动距离(m);Δ为横向间隔距离差(m)。
以子弹3的阻力系数作为基础值,以0.001作为阻力系数的固定步长,以式(8)作为判据,通过Matlab编程,计算得到最小射程条件下子弹2和子弹1的阻力系数,及3个子弹弹道诸元。
在该射击条件下,当子弹2和子弹1的阻力系数分别为0.225和0.499时,子弹的横向间隔距离为最佳距离,其弹道诸元变化曲线如图11~图13所示。

图11 子弹纵向距离随时间的变化曲线图
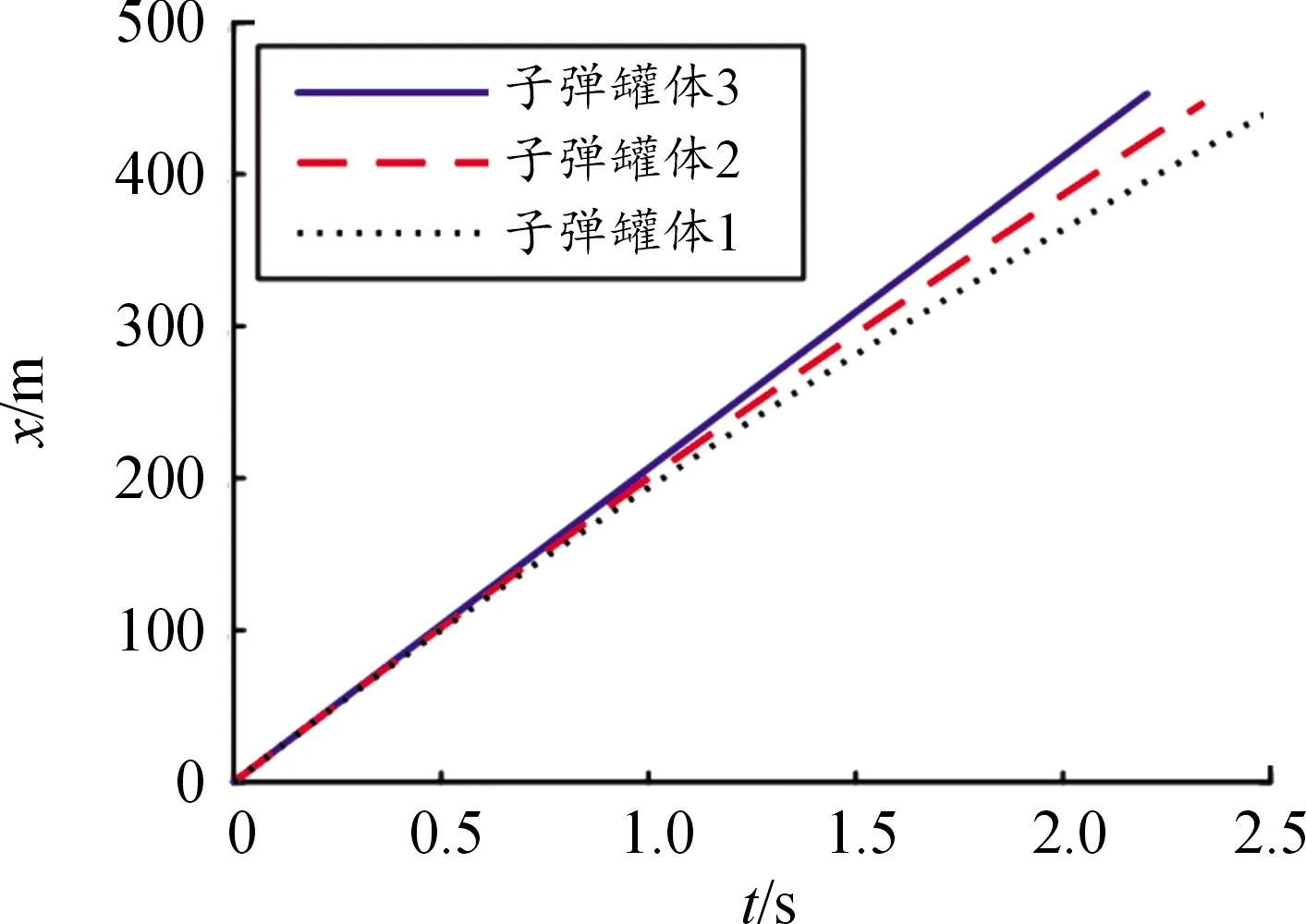
图12 子弹横向距离随时间的变化曲线

图13 子弹运动速度随时间的变化曲线
由图11可知,距离地面高度为10 m时,子弹起爆,子弹1、子弹2和子弹3从抛撒点到达预定高度的时间分别为2.492 s、2.34 s和2.203 s。由图12可知,子弹1、子弹2和子弹3从抛撒点运动到预定的起爆高度,横向距离分别为441.2 m、447.2 m和453.2 m,相邻罐体间的距离差为6 m的最佳距离,与既定条件相符。由图13可知,由于子弹3没有加装阻力翼片,其升力作用小,纵向距离下降最快,由抛撒点运动到起爆高度时间最短,运动速度的改变量小。
4 发烟弹爆炸分散试验与分析
为验证子母式发烟弹装药结构和最佳子弹间隔的合理性,开展了三罐轴向并联间隔起爆的野外测试试验。将3个子弹轴向并联组合且同时起爆,子弹悬挂的横向间隔为6 m。场地布设如图14所示。

图14 三罐轴向并联间隔起爆的试验场地布设示意图
利用8~12 μm远红外热像仪,对遮蔽尺寸和遮蔽效果进行了测试,对烟幕扩散及成形过程进行了分析,烟幕对8~12 μm远红外热像仪的遮蔽效果如图15所示。

图15 三罐轴向并联间隔起爆形成烟幕的遮蔽效果图
由图15可以看出,三罐轴向并联间隔起爆形成的烟幕,在1 s时刻能够较好地弥合在一起,形成连续烟幕,说明子弹起爆间隔设定为6 m较为合理。
5 结论
1) 建立了子母式发烟弹全弹道模型。分析与确定了最小射程下干扰弹全弹道的相关参数,通过静态试验证实了子弹起爆间隔的合理性。
2) 提出了基于横向间隔的目标函数法,计算得到子弹2和子弹1的阻力系数分别为0.225和0.499。
