透·示·行·结：程序性知识的教学模型与实施策略

蒋旭华

【摘 要】程序性知识是指做某事的方法、探究的方法，以及使用技能、算法和方法的準则，它以需要遵循的序列步骤的形式出现。这类知识的教学应遵循“为会用而教”的理念，让学生对所观察的现象、过程或结果进行原理解释，让学生操作演示某一行为动作或动手解答某一算法问题，让学生用所学方案、步骤解决“新”问题，让学生梳理归纳解决问题的步骤或思维流程。在教学过程中，教师应制造认知冲突、创设问题情境、巧用教学支架，以达成学生理解性、迁移性和创造性使用程序性知识。

【关键词】程序性知识 说理 示范 实践 梳理

对于程序性知识的教学，我们不能简单地认为就是让学生识记做某事的操作过程或流程，而是要让学生经历一系列“做”的活动。学生在动手的过程中理解为什么如此做，梳理出做事的相关程序并能学以致用。程序性知识的学习更像旅游中的“自驾游”，学生要经历路线设计、景点选择、食住安排、门票购买等一系列的理性思考活动，然后按照既定的旅游计划亲自游览一个个具有迷人风景的旅游景点并形成“旅游攻略”，即我们所说的“程序性知识”。

一、教学特征

1. 示范性

程序性知识是一套办事的操作方案，是关于“怎么做”的知识。这类知识是根据操作原理和任务要求转化而来的。无论是程序性知识的形成过程，还是其作为最终的结果，教学过程中的操作示范都尤为重要，因为它有利于学习者形成正确、规范、稳定的操作流程。

2. 生成性

程序性知识的构建往往要经历“核心问题—交流讨论—流程显化”这样一个过程。在教学时，学生围绕核心问题主动构建操作思路，通过“试错—纠错—提炼”的学习经历，在交流讨论中逐步形成一套完整的操作流程。所以，程序性知识是逐步析出、动态生成的。

3. 步骤化

依据“做中学”理论，核心问题的解决是在“做”的过程中理解原理、在理解的基础上形成解决方案。学生需要在学习活动中理解为什么要这么做，要讨论梳理该怎样做，进而总结归纳出完成学习任务的步骤。所以，程序性知识的教学呈现出思维路径、操作过程步骤化的特点。

二、表单设计：从原理到操作

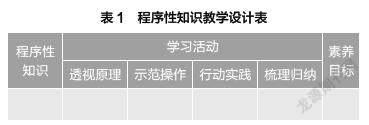
根据程序性知识教学的设计理念与特征，我们可以把它转化为一个教学设计表（如表1）。学生如何获得并形成某一问题解决的程序性操作步骤，需要经历诸如透彻理解原理、操作示范过程、实践体验强化、梳理归纳步骤这样一个从原理到操作的学习活动序列。教师可以根据表1的思路框架进行学习活动与教学目标的设计。

三、教学模型：说理·示范·实践·梳理

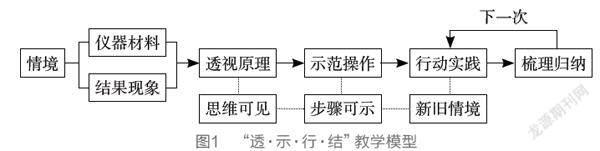
程序性知识的教学要经历说理、示范、实践和梳理等活动环节。说理即学生结合教师的引导对观察的现象、结果或过程进行原理上的解释，能够让即将行动的思想可见;示范即学生能操作演示或表演某一行为动作，或能动手解答某一算法问题;实践即学生能在类似的任务情境中运用所学的方案与步骤解决问题;梳理即学生让操作的程序可见，用流程图的形式或概括性语言把隐含在操作过程中的步骤或“思维”进行小结归纳和外显化，并最终内化到自身的知识结构中去。程序性知识的教学模型如图1所示。

案例：科学九年级上册“找杠杆最小力”操作程序的教学活动。

程序性知识：根据杠杆五要素作图方法，结合杠杆平衡条件，习得在杠杆上作最小力示意图的方法。

教学目标：围绕“如何找杠杆上的最小力”这一核心问题，学生通过“独立思考—尝试作图—交流讨论—纠错优化—程序梳理”等学习活动，总结归纳出作杠杆最小力的一般程序，提升杠杆力臂作图的能力，加深对杠杆平衡条件的理解，初步获得“模型建构”的学科素养。

四个教学活动如下：

（1）明晰杠杆原理，形成操作逻辑。第一，学生结合杠杆平衡条件F1l1=F2l2，经思考、交流、讨论，明确画最小力的关键是画最大力臂;第二，根据直角三角形斜边最长原理，知道最大力臂是支点和力的作用点的连线;第三，根据力臂定义作出该连线的垂线;第四，根据作用在杠杆上动力与阻力的特点确定力的方向。

（2）展开纠错分析，示范操作方法。学生结合操作思路尝试画杠杆上的最小力;教师结合学生作图中的典型错误，引导他们展开纠错分析，并示范（板书）完成最小力的正确作图。

（3）设置问题变式，学会应用提升。教师呈现情境变化的作杠杆最小力的典型例题，让学生操作并展示，进一步巩固并提升作杠杆最小力的操作流程。

（4）采用精练词句，归纳梳理步骤。教师引导学生基于实践过程、采用关键词句归纳作杠杆最小力示意图的一般程序是：明确杠杆支点→确定所画力的作用点→连线作用点与支点→画作用点与支点连线的垂线→确定力的方向。

四、教学变式：提取·应用·构建

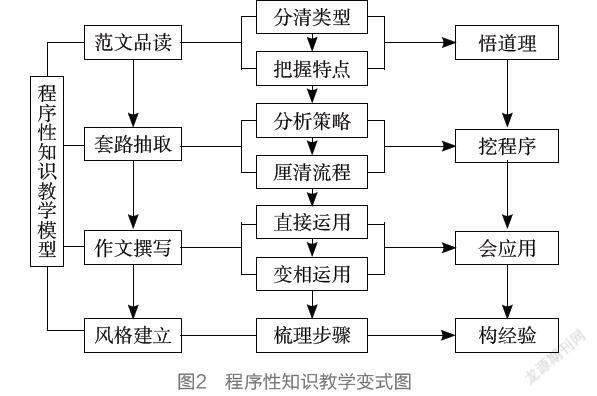
以上教学模型对数学、科学学科的程序性知识教学具有较强的应用性。对语文、英语学科的程序性知识特别是如何写作的程序性知识来说，我们可以基于“透·示·行·结”教学模型的内涵进行转化（如图2）。图2中的“悟道理”“挖程序”“会应用”“构经验”充分体现了程序性知识教学所关注的程序的合“原理性”、可操作性以及重建构性，也与“透·示·行·结”教学模型具有本质上的一致性。

五、教学策略

1. 制造认知冲突，明晰操作原理

程序性知识的背后隐含着丰富的概念性知识。换言之，程序性知识的操作过程是有对应的逻辑和原理作为支撑的。在教学过程中，教师需要制造与程序性知识操作结果相反的认知，顺势让学生理解“为什么不能如此操作”，从而让他们挖掘出正确的操作方法。比如，在浙教版数学七年级上册第二章第四节“有理数除法”的教学中，计算10÷（2+5）时，教师故意采用负迁移—乘法分配律，得出原式=10÷2+10÷5=5+2=7，使学生产生认知上的冲突，以此进一步巩固除法的意义是“把一个数平均分成几份，求一份是多少”，再让学生厘清运算顺序：先算小括号里的数，再算除法，得到的答案是  。

2. 创设问题情境，分解操作过程

教学实践表明，学生理解了操作原理，绝不等于他们学会了“如何操作”。在教学过程中，教师还需要将程序性知识分解在一系列相互关联的“小问题”中。学生在解决每个小问题的过程中，会探索出相应的操作经验，多个操作经验的逻辑组合即构成了解决某一问题的程序性知识。比如，在物体的受力分析教学中，教师可通过问题链层层设问、析问、释问，从而让学生完成对物体的受力分析。是对哪个物体进行受力分析？该物体是否受重力？该物体与另外哪些物体相接触？这些接触的物体对该物体是否有弹力（推力、拉力、提力、压力、支持力）作用？该物体与其接触的物体间是否存在摩擦力？教师逐步引导学生思考，并在思考的过程中逐渐清晰受力分析的一般流程：找准研究对象—判断是否受重力—分析周边接触力。

3. 巧用教学支架，构建操作流程

程序性知识其实是一套解决问题的办法。这套“如何做”的經验是由多个连续的操作步骤组成的，具有一定的结构性。如果学生所学的程序性知识是零散无序的，将不利于他们解决与之相关的同类问题。在教学过程中，教师可提供操作流程的半成品让学生填空，可提供操作流程的要素让学生逻辑排序，也可让学生借助教师的板书或同伴的讨论成果把操作流程用思维导图的形式进行可视化的搭建等。比如，在“抓住细节”这节作文课的教学中，教师出示一幅人物油画《父亲》，让学生观察人物细节。教师板书时归类细节，让学生生成人物细节观察的不同角度，以启发写作思维，形成人物细节描写的策略支架，即拉长时间、延展空间和放大细节。学生可以明确地获取一般人物描写的思维路径：第一层，从人物本身出发，通过放大细节的方式，从外貌、动作、语言、神态、心理等角度捕捉人物细节，其中外貌是值得重点描绘的部分;第二层，通过延展空间的方式，发现与中心人物相关的人物、环境等，再通过拉长时间的联想，为一个平面的人物加入充满时间张力的故事。如此一来，学生就能够真真切切地知道如何去为自己的文章拾取瓦片，且在遇到瓶颈时，不断回溯这一思维路径，从不同角度发现不同的写作素材。

六、检验评价

1. 理解性使用—能正确实施特定的操作程序

程序性知识表现为各具体学科的操作技能、技术和算法的知识。如果学生能准确使用这些“算法”解决各学科的具体问题，就表明他们基本理解、会用那些特定的程序性知识。比如，在道德与法治八年级上册第五课“法不可违”的学习中，对于行政违法、民事违法、刑事违法的区分，如果学生能采用列表的方式融合案例、法律归属、承担责任以及对社会的危害程度来辨别各种违法情况，就表明他们已经习得了区分不同概念性知识的操作程序。

2. 迁移性使用—能用程序解决同类实际问题

程序性知识的“算法”从原理上说是“不变”的、从操作上看是“固化”的，但需要解决的问题往往具有情境性、内外不一致性。如果学生能从原理的视角研究“新”问题，然后从操作的视角解决“新”问题，就表明他们能透过现象看本质、能真正地迁移知识。比如，在浙教版数学九年级上册第1章二次函数的教学中，要解决的二次函数问题是：“若二次函数y = ‒2x2– 20x + k –50，当x<m时，y随x的增大而增大，则m的取值范围是—。”问题的解决首先要将二次函数的一般式转化为顶点式，然后画对称轴，判断抛物线开口方向，再利用图形结合的思想判断m的取值范围（m≤—5）。学生如果能认识到这是二次函数的增减问题，就会采用相应的问题解决程序。实际上，学生得出正确结果的过程就是他们正确迁移程序性知识的过程。

3. 创造性使用—能把程序物化为新颖性作品

有些程序性知识不仅能解决学科问题，还能转化为现实生活中的优秀“作品”。这些作品充分体现了程序性知识的操作原理与过程。如果学生能用技术和方法制作出具有科学性、创造性的作品，则充分体现了他们的知识理解力和生产力。比如，学生在学习了滑动变阻器的工作原理后，依据“观察实物、分析原理、模范制作”的流程去破解“电子秤”的工作原理，利用弹簧、定值电阻、电源、开关、导线等常见器材设计制作出有一定创意的“电子秤”。

七、教学结论：为会用而教

1. 程序性知识的教学不是让学生记住操作流程

在学科教学中，让学生记住做某事的操作流程很“简单”，效率也很“高”。这样的学习结果就是学生采用“依葫芦画瓢”的方式去解决面临的问题。教学实践表明，这样的程序性知识教学由于缺少原理的支撑、缺少知识发生的过程性、缺少学生学习的体验性，导致学生当时“会”、下课“忘”、做题“错”。

2. 程序性知识的教学应该指向素养，为会用而教

解决问题的过程是一个分析问题特征、寻找工作原理、遵循操作方法的实现过程。这里的程序实质上是一种计算思维。计算思维的背后往往蕴含着原理，原理不通，则思路不顺、方法不当。所以，程序性知识的教学要以问题解决为载体，让学生在问题串中习得原理（如此操作的理由）、转化操作（过程步骤化）、活用流程（能抓住问题本质予以解决），从而培养学生的“计算思维”素养。

本文系2019年浙江省教育科学规划课题“初中学科‘素养态’教学设计与实践研究”（课题编号：2019SC048）的部分研究成果。

（作者单位：浙江省杭州市富阳区永兴学校初中部）

责任编辑：赵继莹