一道中考数学新定义问题的多角度分析

北京市三帆中学 陈立雪 王丽萍

2011年起，新定义问题作为北京中考数学试题的最后一道压轴题，一直受到高度的关注。这类问题“要求学生通过现场学习，理解新定义，结合所掌握的知识和思想方法分析新定义的几何含义，借助几何直观，探索问题与问题之间在数量和空间上的关系，发现解决问题的方法”，不仅能考查学生对数学基本知识、技能和思想方法的掌握情况，还能考查学生运用所学知识分析和解决问题的能力。本文以2012年北京中考数学压轴题的一道新定义问题为例，从定义本身、轨迹、函数、不等式四个不同的角度探讨该问题的解法，挖掘其中的数学内涵。

一、问题及分析

问题（2012北京中考数学第25题）在平面直角坐标系xOy中，对于任意两点P1（x1，y1）与P2（x2，y2）的“非常距离”，给出如下定义：若｜x1-x2｜≥｜y1-y2｜，则点P1与P2的“非常距离”为｜x1-x2｜；若｜x1-x2｜＜｜y1-y2｜，则点P1与P2的“非常距离”为｜y1-y2｜。例如，点P1（1，2），点P2（3，5），因为｜1-3｜＜｜2-5｜，所以点P1与P2的“非常距离”为｜2-5｜＝3，也就是图1中线段P1Q与线段P2Q长度的较大值（点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点）。

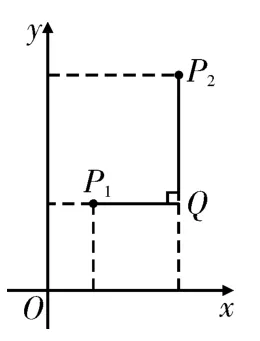
图1

①若点A与点B的“非常距离”为2，写出一个满足条件的点B的坐标；

②直接写出点A与点B的“非常距离”的最小值；

（2）已知C是直线上的一个动点，

①如图2所示，点D的坐标是（0，1），求点C与点D的“非常距离”的最小值及相应的点C的坐标；

图2

②如图3所示，E是以原点O为圆心，1为半径的圆上的一个动点，求点C与点E的“非常距离”的最小值及相应的点E和点C的坐标。

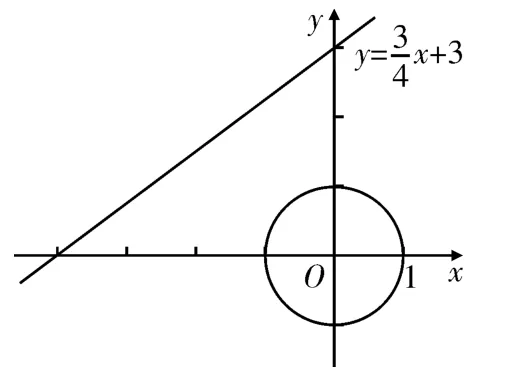
图3

（一）从定义本身的角度解决问题

新定义问题的核心就是定义本身，学生通过题目的叙述认识定义的内涵，通过对实例的辨析来认识定义的外延。但是数学定义本身的抽象性、表述的多样性、内涵的深刻性都是理解的难点。在初中数学中，通常用“文”或“图”的形式表述数学定义，而“式”的表述形式相对较少且比较简单。在高中数学中主要用“文”和“式”的形式表述数学定义，不过“式”的形式更复杂、内涵更深刻。比如，在初中数学中，用“在一个平面内，一条线段绕它的一个端点旋转一周，另一个端点所形成的图形”“到定点的距离等于定长的点的集合”等“文”的形式表示圆的定义，没有出现圆的“式”的定义形式，而在高中数学中出现了用方程（x-x0）2＋（y-y0）2＝r2表示圆心在（x0，y0）且半径为r的圆。又如，直线方程在初中数学中只有斜截式，而在高中数学中还有“一般式”“点斜式”“截距式”等形式。

这道中考题给出了平面直角坐标系中2个点的“非常距离”的定义，即平面内两点P1（x1，y1）与P2（x2，y2）的“非常距离”为max｛｜x1-x2｜，｜y1-y2｜｝，这是属于“式”的表述形式。若用“文”的形式，则可表述为平面内两点P1（x1，y1）与P2（x2，y2）的“非常距离”为这两点在水平方向的距离｜x1-x2｜与竖直方向的距离｜y1-y2｜的最大值。这两种表述形式都比较抽象，不好理解。如果能将定义的“式”或“文”的表述形式进一步转化为“图”的表述形式，则有助于学生理解这个定义和解决问题。

如图4所示，过点P1（x1，y1）画直线y＝x＋b与直线y＝-x＋d，则：

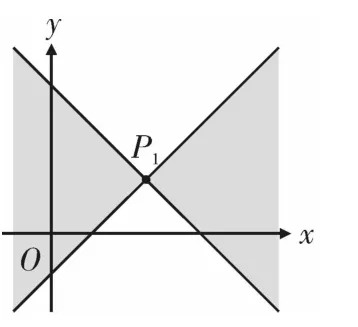
图4

当点P2（x2，y2）在这两条直线上或位于图中阴影区域时，｜x1-x2｜≥｜y1-y2｜，此时点P1（x1，y1）与点P2（x2，y2）的“非常距离”为｜x1-x2｜；

当点P2（x2，y2）位于图中白色区域时，｜x1-x2｜＜｜y1-y2｜，此时点P1（x1，y1）与点P2（x2，y2）的“非常距离”为｜y1-y2｜。

以上就得到了“非常距离”定义更为直观的“图”的表述形式。下面，我们综合运用该定义的三种表述形式解决问题。

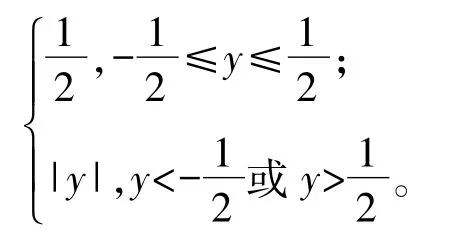
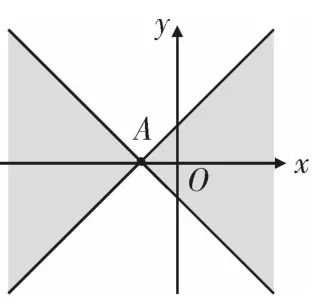
图5

所以，点B坐标为（0，2）或（0，-2），点A与点B的“非常距离”的最小值为

（二）从轨迹的角度解决问题

在初中数学中虽然没有出现“轨迹”一词，但是学生仍然接触了一些描述点的轨迹的概念。例如，圆是到定点的距离等于定长的点的集合（轨迹），角平分线是到角两边距离相等的点的集合（轨迹）。这些与高中解析几何中的某些概念可以联系起来，例如，椭圆是到两个定点的距离之和为定长的点的轨迹，抛物线是到定点和定直线距离相等的点的轨迹。需要指出的是，初中研究点的轨迹，多着眼图形的几何性质，而高中则是从对“轨迹”的直观认识上升到图形与方程的关系，用代数的语言来描述图形的几何特征。

下面，我们从动点轨迹的角度解决这个新定义问题。

设P1（x1，y1）为平面上的定点，动点P2（x2，y2）到P1（x1，y1）的“非常距离”为定值d。由定义可知，如果｜x1-x2｜≥｜y1-y2｜，则｜x1-x2｜＝d，｜y1-y2｜≤d；如果｜x1-x2｜＜｜y1-y2｜，则｜y1-y2｜＝d，｜x1-x2｜＜d。所以，与定点P1的“非常距离”恒为d的动点轨迹是如图8所示的正方形。

图8

根据上面的分析，我们可以得到这个新定义问题的如下解法。

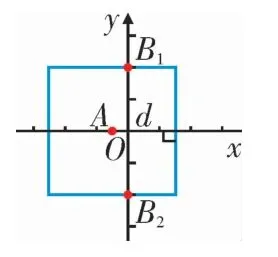
图9

②当正方形的边长从0逐渐增大，且刚好与y轴有公共点时，如图10所示，得到点A与点B的“非常距离”的最小值为

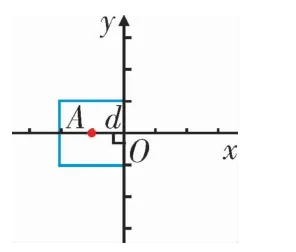
图10

（2）①当动点到定点D（0，1）的“非常距离”d从0逐渐增大时，如果所得的动点轨迹刚好与直线有公共点，则这个公共点就是所求的点C，如图11所示。解方程组，则点C和点D的“非常距离”最小，且最小值为

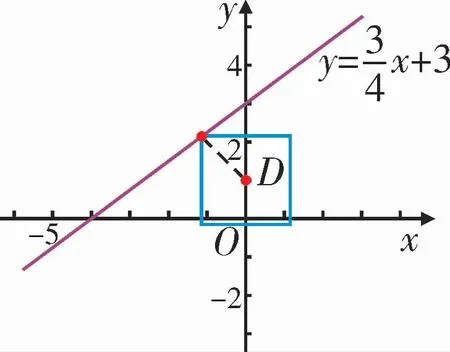
图11

②当点E是圆O上任意一点时，类似于①的情形，可以找到“非常距离”最小时对应的点C。如图12所示，过点E作直线的垂线段EF，垂足是F。由于∠CEF的大小不变，故当EF最短时，CE也最短，相应的“非常距离”也最小。

图12

如图13所示，过点O作直线的垂线段OF，交圆O于E。容易计算得则点C与点E的“非常距离”最小，最小值为1。

图13

在本部分，我们将“非常距离”的定义从“式”的形式转化为“图”的形式，使定义更加直观，进而可以采用数形结合的方法解决问题。2013年，屈奇峰深入地研究了“非常距离”下的圆、中垂线和第一定义下的圆锥曲线。

（三）从函数的角度解决问题

函数的学习贯穿了整个中学阶段，初中阶段学习函数要求理解函数与对应的方程、不等式的关系；而高中阶段学习函数要求能对简单的实际问题，选择适当的函数构建数学模型来解决问题。

下面，我们从函数的角度解决前面的新定义问题。

在平面直角坐标系xOy中，对任意两点P1（x1，y1）与P2（x2，y2），记z1＝｜x1-x2｜，z2＝｜y1-y2｜，则点P1与P2的“非常距离”为z3＝max｛z1，z2｝．借助函数z1，z2，z3的在平面直角坐标系下的图象，我们便可以得到这个新定义问题的一种解法。

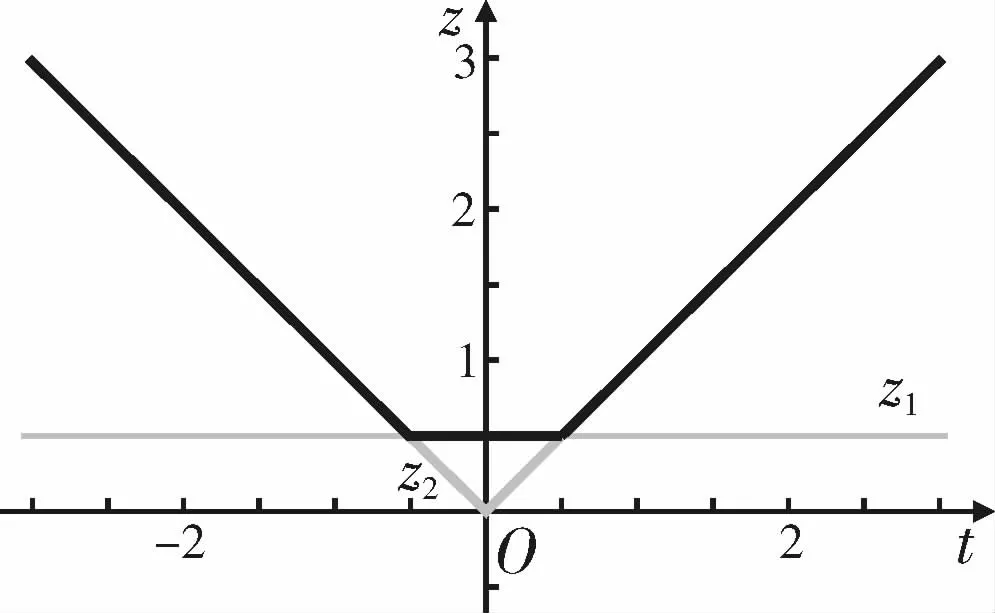
图14

①由图象知，当z3＝2时，｜t｜＝2，t＝±2，所以点B的坐标为（0，±2）；

②由图象知，z3的最小值为

（2）设点C的坐标为

①已知D（0，1），则它们都是关于x的函数，其图象如图15所示。由此可以得到z3＝max｛z1，z2｝的图象（图15所示粗线部分）。

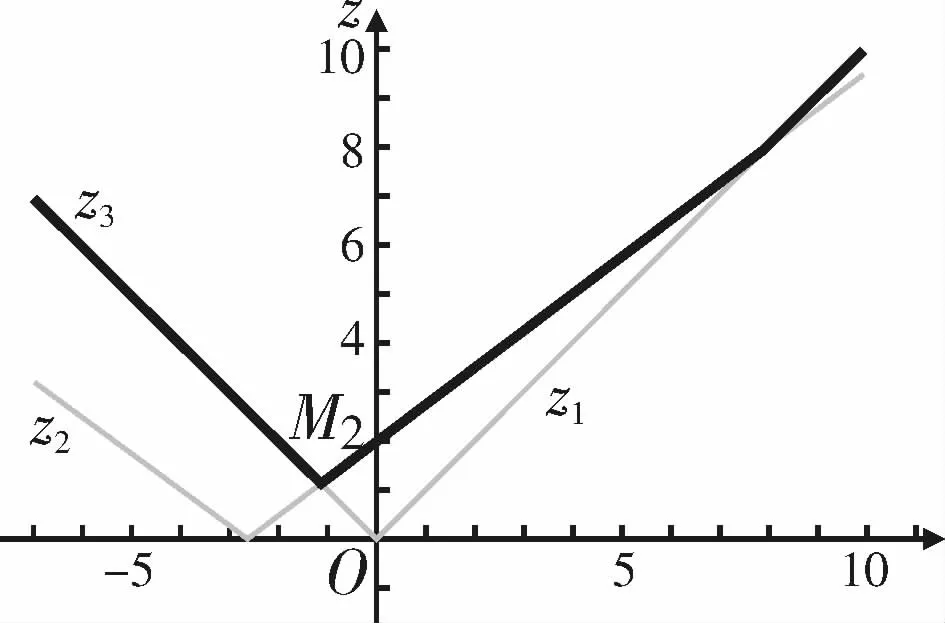
图15

由z3的图象知，函数z3在点M取最小值。

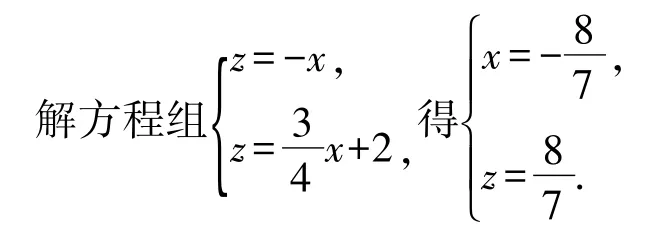
所以，点C与点D的“非常距离”的最小值为此时

②设点E（u，v），则z1＝其中u2＋v2＝1。将它们视作关于x的函数，画出图象，如图16所示，由此可得到z3＝max｛z1，z2｝的图象，图16所示粗线部分。

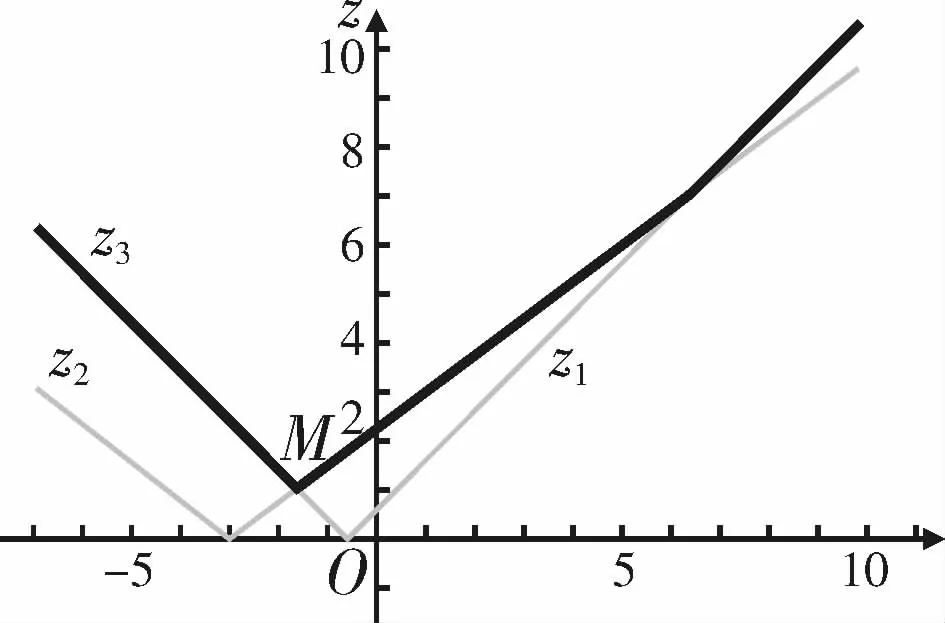
图16

由z3的图象知，z3在点M处取最小值。下面来求点M的坐标。

令a＝3u-4v，则要使z3的值最小，即要使a＝3u-4v的值最小。

考虑点E的坐标为（u，v），所以点E在一组平行直线上。又因为点E在单位圆O上，所以要使直线与圆O有公共点。如图17所示，当a取最小值时，直线与圆相切于点E。

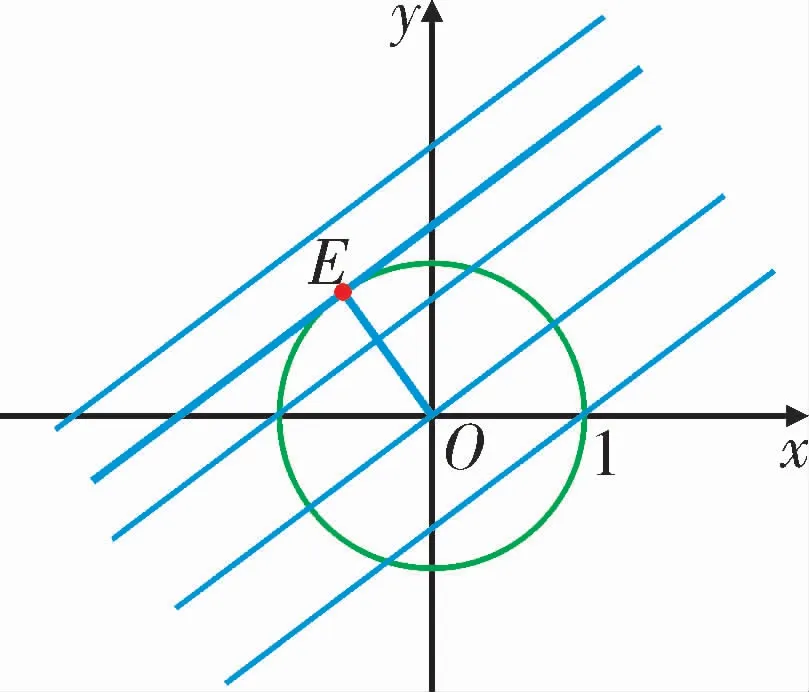
图17

此时，点E的坐标为

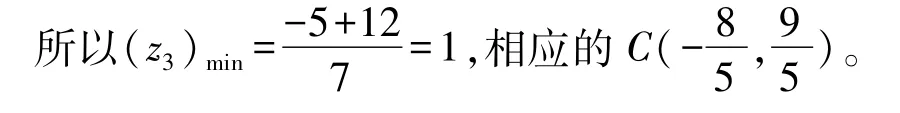
初中阶段学习的函数概念突出了“变化”的特征。本部分内容从函数的角度解决问题，首先通过构造函数，描述“非常距离”随点的位置的变化而变化的情况，然后通过求函数的最小值使问题得到解决。其中，构造函数是关键，将函数的解析式和图象结合起来完成这个过程，既使“变化”的情况精确、直观，又符合初中学生的认知特点。

（四）从不等式的角度解决问题

对于前面a＝3u-4v的最小值，我们还可以从不等式的角度来解决。众所周知，对任意实数a，b，c，d，下面的式子始终成立：

其中等号成立当且仅当ad＝bc。

因为点E（u，v）在单位圆O上，所以u2＋v2＝1。于是，

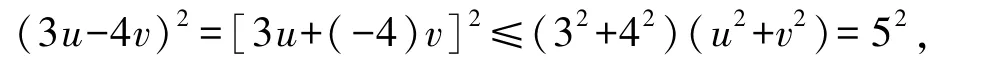
所以｜3u-4v｜≤5，即-5≤3u-4v≤5。

接下来，我们考虑等号成立的条件。

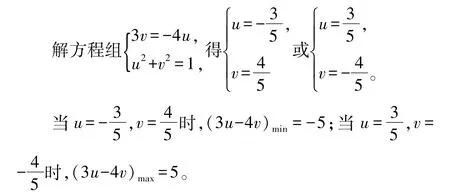
从不等式的角度解决问题，突出了对代数式进行变形和推理的过程，难点在于对等号成立的条件的分析。相比前两种方法，这种方法是对纯粹的数量关系进行分析和推理，具有较强的技巧性和抽象性。

二、对问题的回顾与反思

本文选取了一道与“距离”有关的新定义问题，以初中学生可以接受的知识为载体，分别从定义本身、动点的轨迹、函数与不等式的角度探究问题解法。从这道题的不同解法中，我们可以看到分析和解决新定义问题的一些典型思想和方法，希望对初三备考及初高中知识衔接有积极的意义。

（一）用不同的语言描述数学概念

在新定义问题中，新的数学概念的出现，通常是建立在学生已有数学知识的基础上的，而描述这个新概念的内涵，可以用图、文、式等形式。如果学生能通过自己的理解加工，将新概念转化成不同的表述方式，就能更全面地把握概念的内涵与外延。尤其当这个概念既有“式”或“文”的表述，又有“图”的表述时，就更便于从形的方面直观认识和分析，从数的方面准确计算和验证，使问题解决起来更加得心应手。

（二）用运动的视角分析变化过程

动点的位置发生变化，数量关系也会发生变化，这是很多新定义问题的特点。此时可以从全局着眼，考查动点在完整运动过程中的变化趋势，以便找到普遍规律或抓住关键节点。比如，在这道中考题中，多处出现了“某点是某图形上的一个动点”这样的条件。在第一种方法中，考查动点C的完整运动过程：从形的角度看，点C是从直线的左侧无穷远向右一直运动；从数的角度看，点C的横坐标取值可以为全体实数。

（三）用函数的方法解决变化问题

函数是描述变化过程的数学工具，在分析变化过程后，借助函数的方法刻画这个过程。一方面，函数的解析式能准确刻画变量之间的数量关系；另一方面，函数的图象可以把复杂的变化过程直观化。在上面的第三种解法中，我们把函数的解析式和图象有机地结合起来，更加精确且直观地刻画了动点C的变化过程。

（四）用更高的观点看待问题背景

这道中考题中的“非常距离”可以看作平面上两点的闵可夫斯基距离的一种特殊情形。具体设p≥1为常数，A（x1，y1）与B（x2，y2）是平面上任意两点，则点A与B的闵氏距离定义为

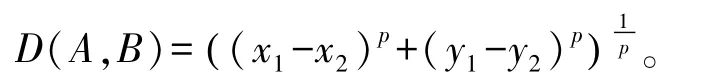
特别地，当p＝2时，点A与B的闵可夫斯基距离就是大家常用的欧氏距离；当p＝1时，点A与B的闵可夫斯基距离又叫“曼哈顿距离”，它被形象地称为“出租车距离”或“城市街区距离”；当p→∞时，点A与B的闵可夫斯基距离又叫“切比雪夫距离”，也就是这道中考题中的“非常距离”。

需要指出的是，闵可夫斯基距离的定义可以推广到高维空间中，它在机器学习、聚类分析、仓库物流等方面有广泛的应用。