基于PQCD 框架下双光子到标量介子对过程中波函数模型研究

余秀

（西南大学，重庆 400715）

双光子到标量介子对的散射过程定义为遍举过程（Exclusive process），对于该过程的研究一直是微扰量子色动力学（PQCD）最具有挑战性的测试领域之一。当微扰QCD 应用到遍举过程时，我们可以发现，强子（介子或者重子）过程的散射振幅可以因子化为部分子硬散射振幅TH和强子分布振幅 ϕ的卷积形式，其中TH部分是微扰论可计算的，而强子价夸克态分布振幅 ϕ由于不能利用跑动耦合常数来计算，需要依赖相应的波函数模型作光锥展开近似处理，本文便介绍了PQCD 框架下对双光子到标量介子对SS 过程中波函数模型的研究。

众所周知，夸克模型在描述强子的性质时非常成功。早在1964 年，M.Gell-Mann 和G.Zweig 就分别独立地提出了“Quark/Aces”模型。他们认为强子（介子和重子）是由三种更基本的费米子“Quark”或“Aces”组成的。而对于标量介子的识别在实验上是困难的，同时标量介子的底层结构也没有建立，在理论上也还不确定。所以虽然轻标量介子被广泛认为主要是四夸克束缚态，但在实践中，很难根据四夸克的轻标量图进行定量预测。因此，我们对标量介子的两夸克模型进行了预测。

因此我们在两夸克态模型下，由FeynArts 程序包，在Mathematica 软件中得到双光子到标量介子对SS 散射过程的拓扑结构，将费曼图可视化，共有20 个树图阶费曼图对rr→SS 过程有贡献，可见附录。下面主要列出两个典型的对该过程领头阶QCD 有贡献的最低阶费曼图。

图1 中，上边的费曼图对应8 种结构，下边的费曼图对应12 种结构。其余的费曼图可以通过初末态粒子交换，胶子传播子的插入位置等对称性分析得到。

图1

在两夸克模型中，轻标量介子的味道波函数被记为：

等式（6）中给出的LCDAs 的定义可以组合成一个矩阵元素

表1

表2

表3

在mHSA 中，硬散射振幅和波函数的卷积存在于横向动量表示的b 空间中，因此我们需要在b 空间中将波函数进行傅里叶变换

在整个计算过程中，将末态标量介子展开为不同的twist光锥波函数，最高讨论已经展开到twist-3 波函数的部分。以上便是我们得到的twist-2 和twist-3 波函数模型以及相关参数的值，可以观察到，在进行傅里叶变换部分，我们初步可以利用指数部分，可以将端点x=0 和x=1 区域的发散压低，但后续计算发现，这种压低还不够明显，计算出的端点值大大超过预期值，也就是说，仅仅利用指数部分还并不能完全消除端点发散的问题，因此在后续的工作中，我们还讨论了从以下两方面来消除端点发散的问题。

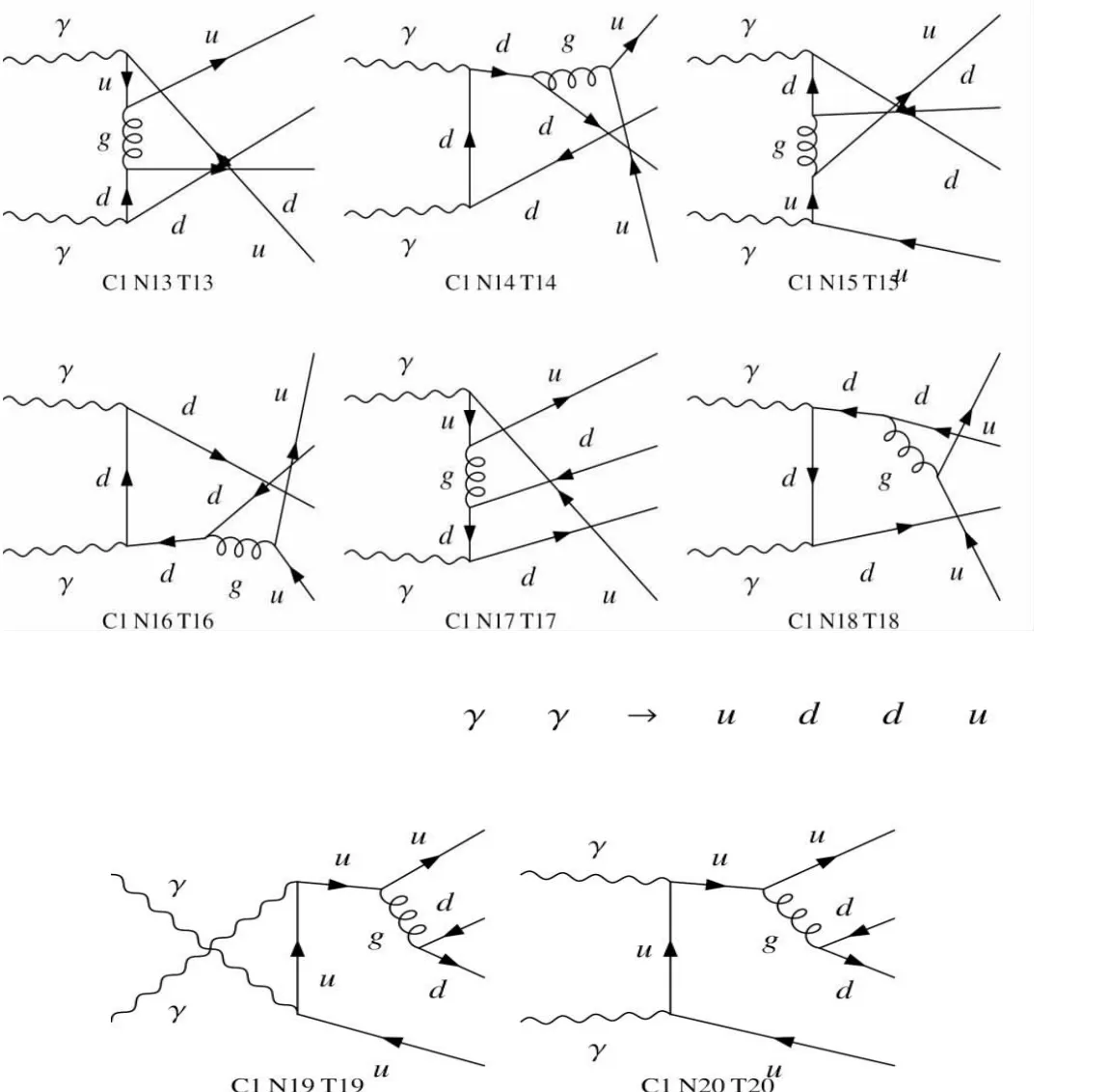
图2