基于频谱和瞬时自相关的雷达信号调制识别

王国涛，姜秋喜，刘方正，孙 兵

(国防科技大学 电子对抗学院， 合肥 230037)

1 引言

雷达信号的侦察识别是战场电磁对抗的一项重要内容。随着电子技术的飞速发展，新体制、新用途雷达不断投入使用，信号的形式也愈加复杂，基于辐射源描述字(emitter description word，EDW)的传统信号识别方法已经不能满足现代战场的需求[1]。如何有效拦截敌人发出的雷达信号，快速地提取出目标信号的脉内调制特征，已经成为电子情报(electronic intelligence，ELINT)系统非常重要的一个环节[2]。雷达信号脉内调制识别常用的方法包括小波变换法、瞬时自相关法、短时傅里叶分析法、二维时频分析法和神经网络法等[3-8]。在这些方法中，时域自相关法具有实时性强、原理简单，易于工程实现等显著优势，特别适用于需要对脉内调制方式实时识别的场景。文献[3]提出了基于信号瞬时频率的脉内调制识别技术，对NS、FSK、PSK和LFM四种信号识别效果较好，但是该方法在低信噪比条件下识别成功率不高，而且识别信号的类型也较少；文献[9]基于信号的时域和频域特征对5种信号进行识别，并在FPGA平台上进行现实，满足高采样率电子战数字接收的需求，但是不能对NLFM等复杂信号进行识别；文献[10]基于信号瞬时频率特征对6种典型类型的调制信号进行识别，能够快速完成信号的分类识别，但是文中并没有给出具体的识别方法；文献[11]利用改进的瞬时频率计算方法实现了对4种类型调制信号的识别，该方法提高了低信噪比条件下频率提取的精度，并抑制了频率模糊问题，但是在低信噪比下对信号调制方式识别成功率仍不是很高。在此研究基础上，为解决雷达信号脉内调制方式的快速识别问题，提出了一种基于信号瞬时自相关的幅度和相位特征的识别方法。具体以NS、BPSK、QPSK、FSK、LFM和NLFM这6种调制信号为研究对象，首先根据3 dB带宽将信号粗分为调相信号和调频信号，然后采用累加法和滑动平均法改进瞬时自相关幅度的抗噪性能，通过增大时延值和采样小区间取均值的方法改善瞬时自相关相位的线性特征，最后分别基于瞬时自相关的幅度和相位特征分别对调相信号和调频信号进行类型细分。通过与文献[11]对比，结果显示文中算法的识别率有了较大的提高，在较低信噪比条件下，有良好的识别成功率。

2 信号的瞬时自相关特征分析

假设侦察接收机截获的雷达信号经过下变频、数字采样后得到的解析信号为

s(n)=Aexp{j[(2πnf0+φ(n))/fs+φ0]}

(1)

式中:A为信号的幅度，f0为信号的载频或者是初始频率，φ0为信号的初始相位，fs为采样频率，φ(n)为信号的相位调制函数，不同的调制信号对应的相位调制函数不同。

瞬时自相关是信号自身的共轭与信号时延后的乘积，其表达式为：

(2)

式中，m为时延时间，为大于0的整数，s*(n)为信号s(n)的共轭。由式中形式可知，信号自相关的瞬时相位与时延时间、信号的初始频率和相位调制函数有关，与信号的初始相位无关。

提取R(n，m)的相位如下：

(3)

式中，lm[R(n，m)]和Re[R(n，m)]分别为复数R(n，m)的虚部和实部，arctan(·)为反正切运算。通过反正切运算后得到的瞬时相位取值范围取值被限制在[-π，π]区间，是信号的模糊相位，通过解模糊运算可以得到无模糊的相位值[12]，由此信号的瞬时频率可表示为：

(4)

不同调制信号的瞬时相关函数呈现不同的特征，分析如下：

1) 常规信号(NS)

相位函数为φ(n)=c(c是常数)，瞬时自相关函数为

R(n，m)=A2exp(j2πmf0/fs)

(5)

由公式可知，其信号形式为直流。

2) 相位编码信号(PSK)

相位函数为φ(n)=πφ(k)，其中，φ(k)是相位编码序列，其瞬时自相关函数为

R(n，m)=A2exp{jπ[2mf0/fs+φ(k)-φ(k′)]}

(6)

式中，φ(k)表示在n时刻信号的码元值，φ(k′)表示在n+m时刻的码元值。对BPSK而言，φ(k)的取值范围为0和1；对QPSK而言，φ(k)的取值范围为0、1/2、1和3/2；由此，差值φ(k)-φ(k′)对BPSK信号而言，只有0和1两种，而对于QPSK信号而言则有0、1/2、1和3/2四种。

3)线性调频信号(LFM)

其相位函数φ(n)=kπn2，式中k是调频斜率。其瞬时自相关函数为

R(n，m)=A2exp{jπ[2mf0+2kmn+m2]/fs}

(7)

由表示式可以看出，LFM信号的瞬时自相关为单载频信号，其相位连续且与时间呈线性关系。

4) 频率编码信号(FSK)

以二频编码信号为例，信号有2个频率成分，码元0和1分别对应频率f0和f1，由此可得到二频编码信号的瞬时自相关为

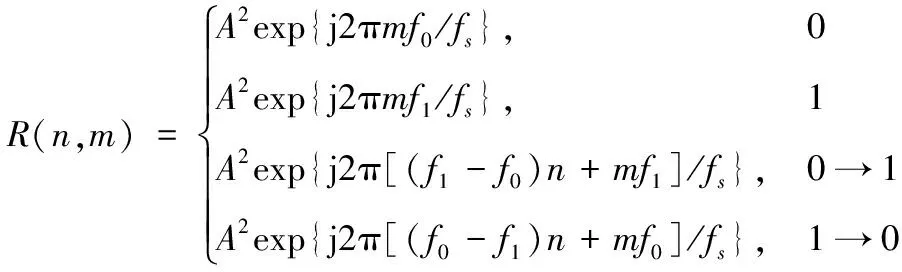
(8)

式中，前两行是n时刻和n+m时刻码元均为0或1时的情况，后两行是两时刻码元跳变的情况，即码元无跳变时信号呈直流状，只有在码元跳变处信号呈单频交流信号。

5) 非线性调频信号(NLFM)

相位函数为φ(t)=π(a0t2+a1t3+…+aN-2tN)，其中，a1、a2、…、aN-2是非线性调频系数，其取值不全为0。为研究方便，本文取3阶非线性，即φ(t)=π(a0t2+a1t3)。由此得到瞬时自相关函数为：

R(n，m)=

(9)

由表达式可知，R(n，m)的瞬时相位连续，与时间n呈二次非线性关系。

3 脉内调制类型的识别算法

6种信号的频谱特征中，NS、BPSK和QPSK信号的带宽较窄；LFM信号的频谱类似一个矩形，信号的带宽较大；FSK信号中有2种不同的频率，频谱图中有2个峰值，2个频率也占用一定带宽；而NLFM也有较大的带宽。由此可以根据信号的3 dB带宽将信号分为调相信号和调频信号两大类，本文称这2种信号分别为PSK信号和FM信号，PSK信号包括NS、BPSK和QPSK信号，FM信号包括FSK、LFM和NLFM信号[10]。对两类信号的细分类均采用基于瞬时自相关特征的识别方法。

3.1 改进的瞬时自相关幅值特征识别法

由第1节分析可知，BPSK与QPSK信号瞬时自相关时域有跳变，但理论上BPSK信号只有一种跳变值，而QPSK信号则有2种跳变值，而常规信号可以看作是一种没有进行相位调制的信号，因此可以通过时域波形跳变点的幅度来区分PSK信号。

图1是信噪比为10 dB的QPSK信号取不同时延m值的瞬时自相关函数时域波形图。从图1中可以看到，只使用单个瞬时自相关特征来识别PSK信号的方法性能较差，一方面是因为相位的变化对噪声比较敏感，直接提取瞬时自相关的幅度或相位特征的抗噪能力不强；另一方面是因为跳变特征受相位偏移量2πmf0的影响，这使得算法存在不稳定性，如图中m=2时跳变处幅度为负值，m=4时跳变峰值特征不明显，m=6时跳变处幅度为正值。

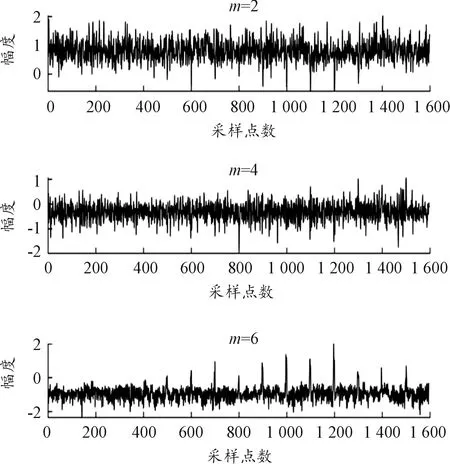
图1 不同m值的瞬时相关函数波形图

基于上述原因，本文改进了瞬时自相关幅度特征的提取方法，以此来提高算法的抗噪性和稳定性：一是采用瞬时自相关累加法；二是对累加自相关进行平滑处理。具体处理过程如下：

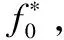
(10)

y(n)=A2exp{jπ[φ(k)-φ(k′)]}

(11)

2) 瞬时自相关累加。假设信号s(n)的n时刻到n+m时刻发生了相位跳变，分别取不同的m值，依次增大并在时域叠加。如果在时延m上取的间隔相等，那么上述过程可以采用如下公式表示：

(12)

式中，L是叠加的总次数。

3) 滑动降噪。滑动降噪法适用于载频较低的信号处理中，能够极大的抑制噪声的影响。滑动降噪处理过程公式如下：

(13)

式中，p是平滑窗宽度。

3.2 改进的瞬时自相关相位特征识别法

从式(7)～式(9)可知：经过瞬时自相关运算后，LFM信号相位与时间呈线性关系，而FSK信号只在码元跳变处与时间呈线性关系，没有跳变的地方相位为常数，NLFM信号与时间呈二次非线性相关。由此可以将瞬时相关函数的相位与时间的最小二乘相关系数r作为信号的识别特征。但是信号相位的变化对噪声比较敏感，由瞬时自相关直接求得的相位抗噪能力较差；而且时延如果取值过小，会使低信噪比条件下信号的特性难以被区分出来[13]，因此直接提取相关系数的识别方法性能较差。如图2所示为SNR=6 dB，m=8时FM信号的瞬时自相关经解模糊运算后得到的相位波形图，可以看到此时的相位受噪声影响较严重，LFM和NLFM信号相位的线性特征被噪声引起的跳变掩盖，这就造成在信噪比较低的情况下算法的性能急剧下降。

为了更好地提取出信号瞬时自相关相位的线性特征，本文做了两点改进：一是增大时延m的取值，增强信号相位的线性特征；二是对相位序列采用小区间取均值的方法来提高算法的抗噪性能。在提取瞬时自相关的无模糊相位后，具体信号处理过程如下：

1) 样本小区间取均值。将采样序列每p个采样点划分为一个区间，共分为M个区间，取每个区间的均值为新的序列，过程表达式为

(14)

式中，θ*(k)为序列的新值。

2) 计算相位序列与时间序列的最小二乘相关系数。相关系数r的计算公式如下：

(15)

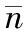
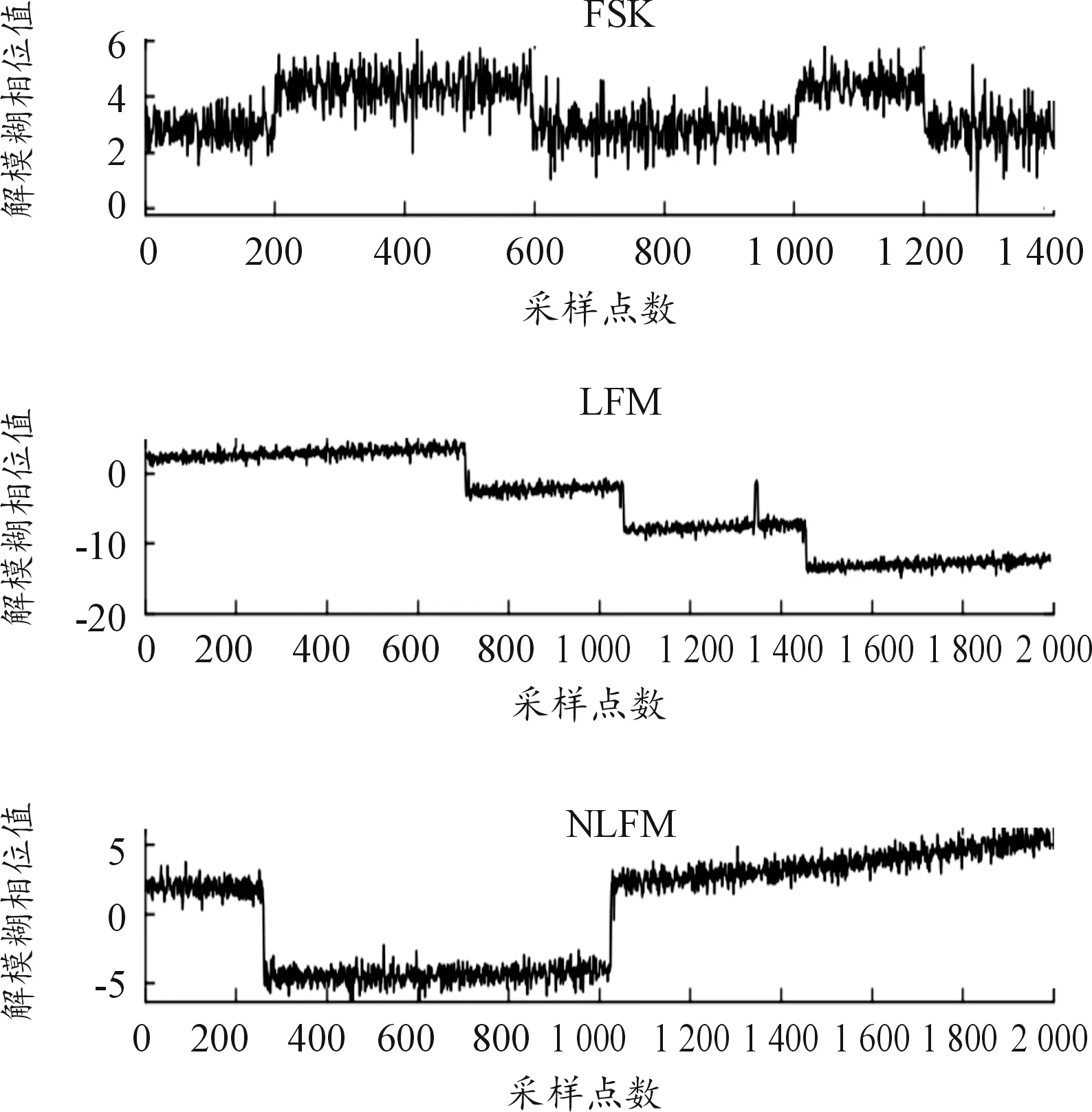
图2 FM信号的瞬时自相关解模糊相位波形图

4 识别算法及实验仿真

4.1 识别算法流程

综合上述分析，将雷达信号脉内调制识别过程总结如下：

1) 对信号做FFT变换提取其功率谱，并对功率谱进行平滑去噪。

2) 提取信号的3 dB带宽，根据带宽将信号粗分为PSK信号和FM信号。提取出PSK信号的载频。

3) 对PSK信号，首先使用载频估计值对信号瞬时自相关的相位偏移进行修正，然后在时域进行累加，最后进行平滑处理，根据过门限的峰值个数实现对NS、BPSK和QPSK信号的识别分类。

4) 对FM信号，首先提取信号自瞬时相关的无模糊相位，然后对相位采用区间平均取样的方法，最后计算相位序列与时间序列的相关系数，根据设定的相关系数阈值区分出FSK、LFM和NLFM信号。

4.2 实验仿真

实验参数设置如下：采样频率200 MHz；NS，BPSK和QPSK信号的载频为20 MHz，BPSK信号采用7位巴克码，子码元宽度为1 μs，QPSK信号采用16位Frank码，子码元宽度为0.5 μs，NS信号脉宽为10 μs；LFM信号初始频率为20 MHz，带宽为40 MHz，脉宽为10 μs；NLFM信号的初始频率为10 MHz，相位调制函数中a0=8.0×1011，a1=2.0×1017，脉宽为10 μs。

图3是信噪比为6 dB时，NS、BPSK和QPSK信号8次累加的结果，时延时间从6个采样点到20个采样点，步长为2。对比图1可以发现改进后的方法信号特征增强明显，从波形图中可以看出，BPSK信号的跳变幅值只有-5一种，QPSK信号的跳变幅值有0和-5两种，而常规信号则基本没有低于0的跳变幅度值，因此可以设置2个门限，一个是σ/2，另一个是σ/2-E(σ是波形的统计标准差，E是序列的统计均值)，统计过2个门限的峰值个数，若过2个门限的峰值个数均为0，则是常规信号；若均大于0，且个数相等则是BPSK信号；若均大于0，且个数差别较大则是QPSK信号。

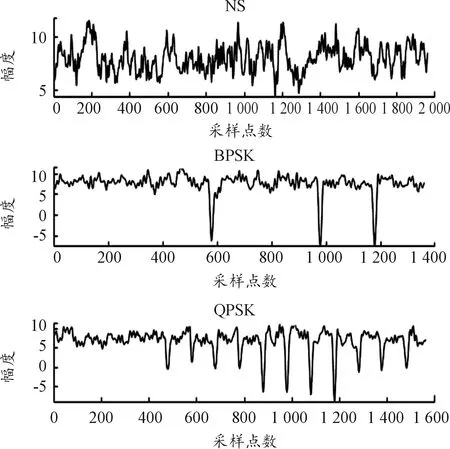
图3 改进后PSK信号的幅度特征曲线

图4显示了使用改进方法提取的FM信号瞬时自相关的相位特征，其中SNR=6 dB，m=128。从波形图中可以明显的看出，在低信噪比条件下虽然受噪声影响，部分相位在解模糊时出现跳变，但是相对于整体影响较小，信号的线性特征有了明显的改善。

图5是FM信号的相关系数随信噪比变化的曲线，该实验中时延为128个采样点。由图中曲线可以看出，当信噪比达到2 dB以上时，3种FM信号的相关系数特征就可以明显地区分出。其中FSK信号的相关系数小于0.3，呈弱相关性，NLFM信号大于0.3且小于0.8，呈中度相关性，而LFM信号大于0.8，呈强相关性，依此可将3种信号进行分类识别。

图6为6种信号在不同信噪比下得到的识别成功概率曲线，该结果为每种信号信噪比每隔1 dB经过200次蒙特卡洛实验得到的统计值。从图中可以看出NS信号由于信号无相位跳变，在信噪比为-2 dB时，即可根据跳变幅值识别出。BPSK和QPSK信号当信噪比大于3 dB时可100%识别出信号。FM信号提取相位后改善性能有限，当信噪比达到5 dB时有近100%的正确识别率。综合以上分析，文中算法可以成功的识别出6种信号，当信噪比大于5 dB时，信号的识别概率接近100%。

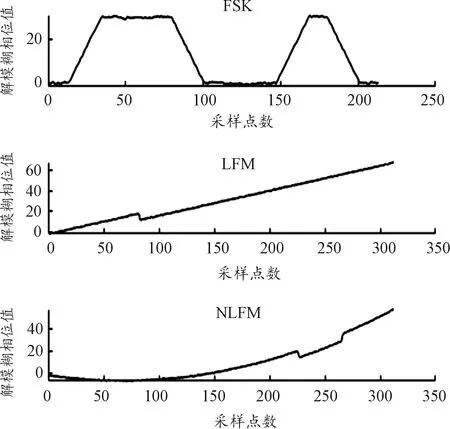
图4 改进后FM信号的相位特征曲线

图5 FM信号相关系数随信噪比变化的曲线

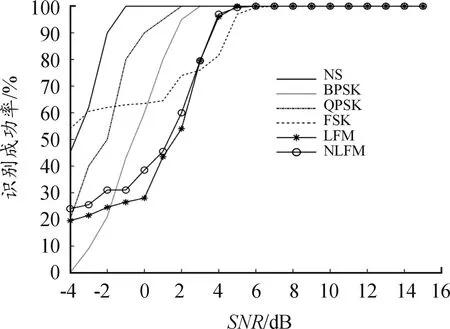
图6 不同信噪比下识别的成功概率曲线

5 结论

文中以NS、BPSK、QPSK、FSK、LFM和NLFM六种调制信号为研究对象，提出了一种基于瞬时自相关幅度和相位特征的信号快速识别方法，该方法将信号瞬时自相关的幅度和相位特征分别应用于调相信号和调频信号的识别。首先根据信号带宽将信号粗分为PSK和FM两大类信号，然后通过时域累加法后进行平滑处理的方法增强调相信号的幅度跳变特征，通过增大时延后对相位进行解相位模糊和采用采样区间取均值的方法增强了低信噪比下调频信号的特征，最后分别根据瞬时自相关的幅度和相位特征完成PSK和FM信号的细分类识别。仿真实验表明：文中方法能够识别6种典型的雷达信号，信噪比高于5 dB时能100%识别出信号，该方法具有低计算复杂度的同时兼有良好的成功识别率。