基于背景差法的网球运动员击球运动轨迹线形捕捉方法

卫扬平

(安徽国际商务职业学院，安徽 合肥 231131)

引 言

随着体育运动的发展，信息技术在体育领域的应用程度越来越深[1-2]，其中将捕捉技术引入网球运动，不仅能捕捉网球运动员的各项动作，并且可以以此为基础，校正运动员动作，提高运动员技术动作的规范程度，强化训练效果[3].但是，对于现阶段而言，由于网球运动员击球运动轨迹特征提取效果不佳，导致击球运动线性轨迹捕捉效果差.相关专家针对该方面的问题进行了大量的研究，例如余乐[4]等人对人手臂末端的Marker标记点位姿矩阵中的信息结构进行全面分解，同时在数据处理过程中获取不同标记点的距离，进而实现位姿矩阵对人体行为的捕捉.程宁波[5]等人通过运动捕捉系统采集人体标记点的位置变化情况，并且分解人体的动态行为，实现运动轨迹捕捉.以上两种方法虽然取得了十分满意的研究成果，但是其仍然无法满足现阶段的高精度运动轨迹捕捉需求.为此，提出一种基于背景差法的网球运动员击球运动轨迹线形捕捉方法.经测试表明，该方法能提高捕捉的准确率，减少计算开销.

1 方法

1.1 小波去噪

首先采集网球运动员击球运动轨迹线形图像，其次，利用小波变换对采集到的图像进行去噪[6-7].小波(mother wavelet)是一个由局限领域内的函数φ(χ)构建的，当傅里叶的转变φ(χ)能够满足式(1)中的条件时，函数φ(χ)被称之为小波，亦可被称之为基本小波：

(1)

将基本小波函数进行拉伸以及平移操作，获取对应小波基函数，如式(2)所示：

(2)

式(2)中，参数a的主要作用是控制收缩范围，有效强化基函数的宽度；参数b主要代表平移，通过该参数能够确定x轴的平移间距取值.因此，针对随机函数f(χ)∈L2(R)，它的无限小波变换能够表示为式(3)的形式：

(3)

其中，Wa,b(χ)是代表函数f(χ)与φa,b(χ)两者之间的内积.同时，在频域上也存在：

(4)

分析连续小波变换的相关理论可知，当参数a的取值过大时，则Wa,b会被无限制拉长；反之，当a的取值过小时，Wa,b则会被无限制压缩.由此可见，参数a为比例因子，能够实时对小波函数的形状进行调整.

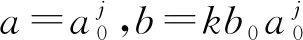
(5)

式(5)中，a0表示大于1的单位拉伸；b0被称为正实数；j、k的取值为整数.函数f(t)的离散小波变换表示如下：

(6)

当a0=2，b0=1时，则离散小波函数可以表示为：

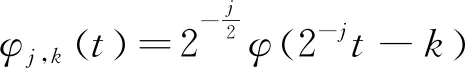
(7)

离散小波函数也能够被称为二进小波，构建如下的小波函数：

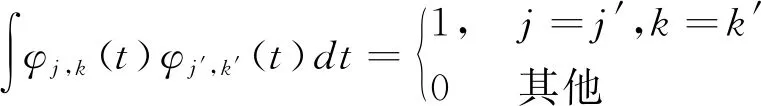
(8)

近似估计小波函数的精度，公式为：

(9)

式(9)的系数被表示为：

(10)

三维图像的小波解析与重构的整个过程主要是在一维信号和重构算法的基础上得到的，具体的操作过程为：首先利用两个滤波器分别对不同图像进行滤波处理，然后进行二取一采样，获取两个相同规格的子图像，接着采用低通滤波和高通滤波同时对子图像进行滤波处理以及采样，获取四个规格相同的子图像[9]，从而实现一层小波分解；其次对一层小波分解中的子图像重复上述操作过程，完成二次小波分解；最后继续重复上述全部操作过程，直至满足最终的需求，以下给出小波去噪的具体操作示意图(如图1所示)：

图1 小波去噪示意图

1.2 网球运动员击球运动轨迹线形特征提取

采用小波变换去噪处理图像为预处理环节，但是仅预处理运动员运动图像无法精准捕捉运动员的击球轨迹，因此，以提取网球运动员击球运动轨迹线形特征为基础，引入背景差法，实现击球运动轨迹线性捕捉，为运动员提供有效的参考.首先，提取网球运动员击球轨迹周围的轮廓特征点，得到网球运动员击球轨迹线性滤波的母小波函数，如式(11)所示：

(11)

对于R个邻近点，当采用母小波中的基函数进行网球运动员击球运动轨迹线形图谱解析时，经过小波转换的网球运动员击球运动轨迹线形的动作像素特征为(θe,pe)，通过多尺度的小波变换方式完成网球运动员击球运动轨迹线形的动态滤波，获取网球运动员击球运动轨迹线形对应的灰度像素集：

(12)

式(12)中，dij(z)表示网球运动员正手击球动作轨迹线形对应像素点的欧式距离；dx(xi,xj)表示图像在4×4的网格中的局限领域活跃轮廓分量[10-14].

通过灰度直方图方法对图像中的灰度信息进行增强，获取对应的像素集和边缘集合，以下给出具体的表达式：

式(13)中，G(χ,y,σi)代表网球运动员击球运动轨迹线形的相似性特征.

上述设计通过小波变换方法获取了网球运动员击球运动轨迹线形的特征向量，完成网球运动员击球运动轨迹线形特征提取.

1.3 基于背景差法的网球运动员击球运动轨迹线形捕捉

在以Iχ为中心的情况下，进行网球运动员击球动作轨迹线形分块特征匹配，提取网球运动员正手击球动作轨迹线形包络线f(gi)，即：

(16)

通过灰度直方图方法可以全面提升运动轨迹线性捕捉结果的准确性.以下是针对不同的灰度量进行的计算，即：

(17)

如果网球运动员正手击球动作轨迹线形的边缘尺度为σ0，采用RGB分解的方法得到网球运动员正手运动轨迹中线形像素特征点为：

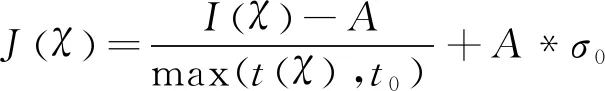
(18)

式(18)中，网球运动员正手击球动作轨迹线形的边缘自相关特征量采用t0表示，边缘自相关特征向量的特征函数采用t(χ)表示.

通过像素自适应方法定位网球运动员击球运动轨迹的线性特征点，公式为：

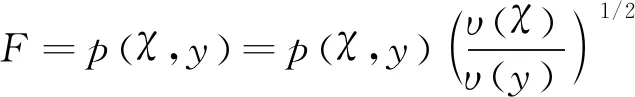
(19)

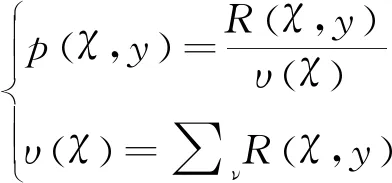
(20)

引入小波变换方法进行尺度寻优，获取网球运动员击球运动轨迹线形的特征向量，完成网球运动员击球运动轨迹线形特征提取：

(21)

式(21)中，f(z)是网球正手击球动作轨迹线形的纹理特征；*代表卷积运算.

设定Iχ代表多分辨的网球运动员正手击球动作轨迹线形，当χ=(P,N)时，网球正手击球动作轨迹线形的活动轮廓为：

(22)

(23)

式(22)中，网球运动员正手击球动作轨迹线形的边缘尺度用Q表示，式(23)中，图像弱边缘的特征用W表示.通过背景差分对网球运动员击球运动轨迹线形进行捕捉，具体的计算式为：

(24)

(25)

通过背景差分法对网球运动员击球运动轨迹线形图像分块进行融合，输出最终的捕捉图谱如下：

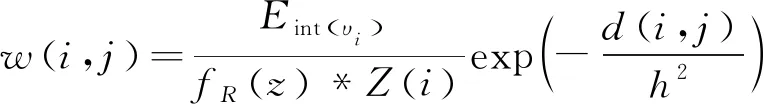
(26)

结合上述分析，通过背景差法可以修正捕捉到的运动员击球运动轨迹线形误差，从而完成精准捕捉运动轨迹线形.

2 仿真实验

为验证基于背景差法的网球运动员击球运动轨迹线形捕捉方法的有效性和可行性，设计对比分析实验.实验在Matlab平台中进行，运动轨迹采样频率为32 kHz，同时调用实验平台中不同函数进行运动轨迹采集，其中测试样本集为200幅图像，通过上述实验环境和参数进行测试.

实验首先对网球运动员击球运动轨迹线形捕捉结果准确性进行对比，将图2作为测试对象，利用图3给出3种不同方法的实验对比结果.

图2 测试对象

(a)本文所提方法的运动轨迹线形捕捉结果 (b)文献[4]方法的运动轨迹线形捕捉结果 (c)文献[5]方法的运动轨迹线形捕捉结果

分析图3中的实验数据可知，本文所提方法能够全面捕捉运动员击球运动轨迹线形.但是文献[4]方法和文献[5]方法仅捕捉到击球运动轨迹的局部过程，说明文献方法的捕捉结果准确性较低，本文所提方法的捕捉结果准确性较高.

为了进一步验证本文所提方法的优越性，以计算开销为实验性能指标，该指标值越低，表明捕捉方法的性能越好，实验采用20个样本，实验共计测试次数为4次，实验过程分别为本文所提方法、文献[4]方法和文献[5]方法，对比三种不同方法的计算开销，具体的实验对比结果，如图4所示.

(a)本文所提方法的计算开销变化情况

分析图4的实验数据可知，本文所提方法的计算开销明显低于另外两种方法，主要原因是：在进行运动轨迹线形捕捉的过程中，本文所提方法对图像进行小波变换，有效滤除图像中的噪声，促使计算开销得到有效降低.

3 结语

本文针对传统方法存在运动轨迹线形捕捉结果准确性较低和计算开销较大等问题，结合背景差分法，提出一种网球运动员击球运动轨迹线形捕捉方法.仿真实验结果表明，本文所提方法捕捉网球运动员击球运动轨迹线形结果更加准确，并且有效降低了计算开销，该方法具备了可行性和有效性，实际应用价值更高.