基于改进贝叶斯方法的基因调控网络构建

饶臻, 郑明

(1.广西大学 计算机与电子信息学院, 广西 南宁 530004;2.梧州学院 大数据与软件工程学院, 广西 梧州 543003)

0 引言

随着人类基因组计划的开始,生物信息学作为一门新的交叉学科而兴起，内容包括对分子生物学数据库的研究和推理、基因之间的调控关系研究等。研究基因之间的调控关系对生物医药的研究有着重大意义,例如人类常见的疾病的发生归根溯源都是基因的异常表达结果,且在基因之间存在促进和抑制的调控关系,调控与被调控的基因之间构成了基因调控网络[1]。传统的通过实验对比进行基因调控网络验证的方法的耗费巨大,因此利用现有的实验样本中的基因表达数据，使用机器学习或统计分析的方法构建基因调控网络，取得对生物研究者有一定指导作用的成果,成为许多研究者广泛关注的问题[2]。

贝叶斯网络[3]模型是一种可以反映变量之间的依赖关系的网络模型,具有可以进行图形化表示,因果关系清楚,可以进行不确定推理等优点,在相当多的领域都有着广泛的应用,研究者们先后将各个领域的问题引入到贝叶斯网络模型中求解,取得了不错的成果。本文采用贝叶斯网络的结构学习来构建基因调控网络,而学习一个由离散变量组成的贝叶斯网络的最优结构在几乎所有情形下都是NP问题,其网络空间随着节点个数的增加呈指数增加,所以只能用启发搜索算法来寻找接近最优的网络,目前主流方向有以下3种:①基于约束的统计分析方法；②基于评分搜索的方法；③前述2种算法结合的混合搜索算法。

基于统计分析的方法通过检测互信息值的方式判定在网络中节点的边是否存在并构建有向图,如最早的SGS[4]算法、改进后的PC[5]算法、FCNSLA[6]算法等。该类学习算法需要依次判别各节点之间的条件独立性,随着网络规模增加,时间复杂度指数级增长,因此该类算法只能适用于较小的稀疏网络。

基于评分搜索的方法则使用启发式搜索来构建有向图,搜索算法和评分函数决定了生成网络的准确度,目前常用的经典搜索算法有爬山(Hill Climbing)算法,需要提供节点序的K2[7]算法等;评分函数有BIC[8]、BDe[9]、MDL[10]等。近几年,评分搜索广泛使用了基于仿生学理论的优化方法,如蚁群算法[11]、人工免疫算法等[12]。

上述2种方法各有其缺点,适用场景也有限，因此,混合学习的方法成为现今研究的重点,此类方法利用独立性测试分析效率较高的优势来约束搜索空间的大小,然后再用评分搜索进行最优网络结构的寻找,最终完成一个最优网络结构。第一个混合学习算法是CB[13]算法,通过PC算法确定节点间的先后顺序,之后再使用K2算法对结构进行学习;MMHC算法[14]是结合稀疏候选算法思想的另一种经典混合学习算法,使用MMPC算法构建贝叶斯网络的搜索结构,再用K2算法来确定最优的网络。已有实验表明,无论从网络的质量还是时间复杂度上来看,MMHC算法都要较优。

本文提出了贝叶斯网络的混合学习算法构建基因调控网络的方法,基于最大信息系数MIC[15]估算各个基因变量之间的关联程度并据此构建初始网络,通过在缩小搜索空间的初始网络上进行评分搜索,构建更加准确的基因调控网络，并在规模较小的单细胞的蛋白质因果表达网络(SACHS)和规模较大的大肠杆菌表达网络(ECOLI)数据集进行了不同样本数量的多次实验,与Hill Climbing算法、MMHC算法等经典算法在3个性能指标上进行对比,验证了该方法的有效性和优越性。

1 理论与方法

1.1 贝叶斯网络

定义1 贝叶斯网络[3]由一个无环的有向图G=(V,E)和一个条件概率表θ构成,在图G=(V,E)中,V={x1,x2,…,xn},表示一个网络中的随机变量集合,xi为随机变量。E是以V中随机变量的有向边的集合,如表示网络中存在x1到x2的边,当存在xi到xj的边时,称xi是xj的父节点。条件概率表θ则表示了各个父子节点之间的条件概率,θi∈θ表示网络中随机变量xi的条件概率分布。

贝叶斯网络的结构学习就是根据给定的数据集D尽可能找出与其最拟合的网络结构模型,并将其用有向无环图表示的过程。拟合程度的评分标准以评分函数计算,本文使用的评分函数为BDe评分函数[9],BDe评分函数使用数据和先验知识查找后验概率最大的网络结构,方便使用且有直观意义。其定义如下:

(1)

1.2 最大信息系数

为了尽量消除对2个变量进行互信息检测时其他变量对相关性判定的影响,使用MIC检测网络中各个基因节点的依赖关系。MIC是针对2个具有一定相关性的变量,利用这2个变量的散点图上进行某种网格划分后的近似概率密度分布进行互信息计算并正则化的值,可衡量这2个向量的相关程度。相较于互信息,MIC具有更高的准确度,不受数据的影响,也不会限定在特定的关联函数种,能够广泛应用且更有公平性,是一种优秀的数据关联性的计算方式。

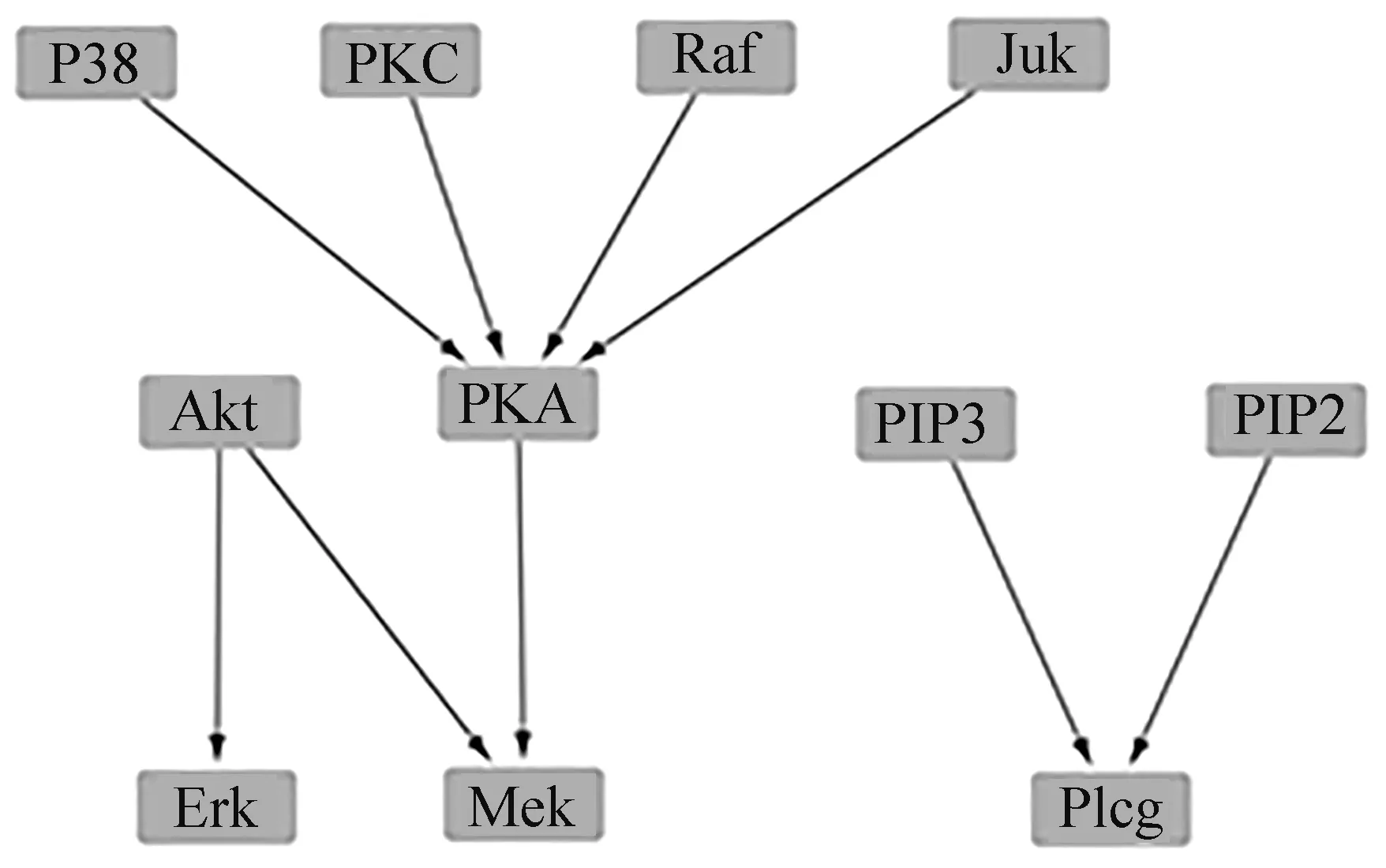
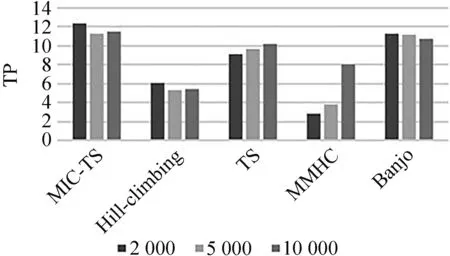
定义2 对于一个含有随机变量X和Y的数据集D,按i行和j列将一坐标平面划分成网格Gr,i*j

(2)

定义3 有限数据集D中的2个节点X和Y的特征矩阵M(D)的公式定义为

(3)

式中I*(X,Y,D,i,j)表示有限数据集D中变量X和Y在网格Gr中的最大互信息值,也即I*(X,Y,D,i,j)=maxI(X,Y,D|Gr)。I(X,Y,D|Gr)为网格Gr下变量X和Y的互信息值,i和j为使得I(X,Y,D|Gr)达到最大值的网格的行和列。

定义4 2个节点变量X和Y在坐标平面的最大信息系数的定义如下:

M(X,Y|D)=maxi*j

(4)

由于随机变量之间的MI存在对称性质,MIC也具有对称性。

1.3 融合方法的贝叶斯网络学习

根据1.2所述的MIC定义,可知MIC值与2个随机变量之间的依赖程度是正相关的,也就是说，如果随机变量X和Y之间的MIC值越大,二者的依赖程度就越高,说明它们在网络中可能相连。反之,如果随机变量X和Y之间的MIC值越小,则依赖程度越低,当2个变量间的MIC值为0时,表示变量相互独立,说明二者在网络中不存在调控关系。本文提出MIC-TS算法,根据MIC构建初始网络以缩小搜索空间并使用优化算法进行评分搜索。下面以蛋白质因果表达数据集(SACHS)为例说明初始网络构建的过程。

首先根据最大信息系数的定义计算数据集中变量之间的MIC值(表1)并根据MIC值进行初始网络的构建。

表1 SACHS网络的MIC表Tab.1 MIC table of SACHS network

根据计算出的MIC值(表1),将每一列(行)中值最大的MIC记为MICmax,如果表中存在变量X和Y的MIC满足式(5),那么变量X和变量Y在网络中可能存在一条边,表中用粗体标注所示。

(5)

式中μ为控制因子。根据Zhang等的研究[12],对于此类稀疏图,μ取值为0.9时,能使得初始网络中添加尽量多的可能存在的边的同时添加尽量少的无关边。

根据表1的标注对所有满足式(5)的MIC值从大到小进行排序,并根据大小顺序在空图G的节点间依次添加有向边以构建初始网络,这样可以最大限度地将关联性更强的边添加到网络中,边的方向为列节点指向行节点,如Erk→Ark,此步骤到所有满足式(5)的MIC值全部判断完毕,得到一个非连通的有向图为止,在添加有向边的时候,有3条规则:

① 在根据MIC值向网络中添加有向边的时候,为了避免出现冗余的边,如果该节点有其他有向边,则跳过该列的判断。

② 如果在添加有向边时,该边的反向边已经存在,则跳过继续判断下一对满足条件的节点对。

③ 当往网络中添加有向边的操作会导致出现环时,则跳过该边继续判断下一对满足条件的节点对。

根据以上的加边规则构造出的有向图如图1(a)所示,可发现使用上述方法并不一定能获得一个连通的有向图,为获得一个连通的有向图,需要继续在图中的连通分量中添加有向边。

假设一个非连通图G由N个连通分量组成,记为G={G1,G2,…,Gn},Gi=Vi,Ei,为了将图G修复成连通图,要在N个连通分量之间添加N-1条边,具体方式如下:设有变量集Vi、Vj,为使两变量集之间相连通,需要在Vi、Vj间添加一条边,并使其满足

MICmax(Vi,Vj)=max MIC(Xi,Xj)。

(6)

计算非连通图中的2个连通分量任意节点的MIC值,并且根据(6)式选取连通分量之间MIC值最大的2个连通分量Xi、Xj,在Xi、Xj之间添加一条有向边,并以此类推直到图G变为连通图为止,如图1(b)所示。

(a) 连通前

(b) 连通后

根据MIC计算出的初始网络能够有效的缩减评分搜索过程中的搜索空间,减少计算过程中的随机性,有效的提高最终网络的准确性。随后以该初始网络作为起点,引入Tabu算法的思想和使用BDe评分函数进行基于评分的网络搜索,在Tabu算法运行中,通过将一些可能使得算法产生重复循环的解置入禁忌表,提高算法效率跳出局部最优,生成最终的基因调控网络(图2),算法如下所示。

算法1 MIC-TS

输入:矩阵化MIC表MIClist,MICmax,E={},DAG={},数据集D

输出:贝叶斯网络DAG

1.For col=1:n

2. For row=1:n

3. IF MIC(Xi,Yj)≥μMICmax(Y)

4. List=sort(MIC(Xi,Yj))//将节点之间的MIC值从大到小排序

5. FOR len=1:len(list)

6. IF(Xj,Xi)∈Eor isCycle(Xi,Yj) // isCycle(Xi、Yj)检查Xi、Yj之间连接边是否会导致图中出现环

7. CONTINUE

8. ELSE

9. add(Xi,Yj) to E//将Xi→Yj的有向边添加到边集合中

10.E→BN

11.DAG=tabu(BN,bde,D)//以BN为初始网络,bde为评分函数,D为拟合数据集进行Tabu搜索

12.Return DAG

2 实验结果与分析

2.1 实验准备

本文中实验使用R语言的Bnlearn包,通过R语言进行编程完成算法进行网络结构学习。R语言的Bnlearn包是一个贝叶斯网络工具包,内置各种评分函数和用于比较的经典算法,主要用于贝叶斯网络结构学习和参数学习等方面,本文使用4.6.1版本。实验的运行环境:Windows10操作系统,64bit,Intel i5-9300H处理器,2.40 GHz,8 GB内存。

为了便于进行性能对比,实验采用了已经验证过的蛋白质因果表达网络(SACHS)和大肠杆菌表达网络(ECOLI)2个标准网络数据集,在Bayesian Network Repository下载标准网络的rda文件,随机生成相应大小的数据集进行实验，见表2。

表2 本文实验使用数据集Tab.2 Data sets are used in this experiment

2.2 实验指标

为了能够评估基因调控网络建立的效率,本文将使用F值和汉明距离值(Hamming distance, HD)对算法生成的网络进行评价以验证算法的有效性。式(7)中,TPR表示真阳率(true positive rate),反映了算法对标准网络中存在的边的预测正确率,TP表示在标准网络和算法生成网络中均存在的边数,FN表示在标准网络中存在,但是算法并没有生成的边数,(8)式中,PPV表示查准率(sitive predicted value),反映了算法预测出来的网络边的准确度,FP表示标准算法中不存在但是算法生成了的边数。由(9)(10)式可知,TP值和F值越高,HD值越低,算法生成的网络就越贴近真实网络。

(7)

(8)

(9)

HD=FP+FN。

(10)

2.3 结果分析

实验中对2个不同大小的标准网络:小型网络SACHS数据集,大型网络大肠杆菌表达网络数据集(ECOLI)进行了对比,将其按照2 000、5 000、1 000的样本量进行采样,与其他经典贝叶斯算法，如 MMHC[14]、Hill Climbing[17]、Banjo[18]、TS[19]等在F值、HD值(汉明距离)、TP(正确边数)这3个指标进行了对比分析,为使实验结果尽量排除随机因素影响,对每个样本量都进行10次采样学习,最后使用10次交叉验证结果的指标的平均值和标准差对比(表3、4),表中括号内的值为10次实验结果的标准差。

表3 MIC-TS与各个算法在SACHS数据集上的实验结果Tab.3 Experimental results of MIC-TS and various algorithms on SACHS data set

对于规模较小的SACHS网络,从表3的数据中可以直观的看出,本文中的MIC-TS算法与其他的结构算法相比,取得了较优的实验结果。从样本数量为2 000、5 000、10 000的实验结果可以看出,本文算法的TP与F值与其他算法相比均为最高,HD值为最低,并且在样本量为2 000时,就学习到了与标准网络完全相同的网络结构(图3所示),说明了本文算法在该数据集上生成的网络相较于其他经典算法更接近于真实网络,相较于Hill Climbing、MMHC算法有明显的优越性;MMHC算法由于其仅在缩减后的搜索空间进行搜索,在样本量不足(2 000、5 000)时,构建的搜索空间并不准确,在减少假阳率的同时,能搜索到的正确边也会变少,导致在性能上不如Hill Climbing算法,而样本量充足时(10 000),MMHC的性能会有较大的提升,生成网络稳定,实验标准差为0,此时各项指标优于Hill Climbing算法。表中的Banjo算法和TS算法在该数据集上的实验也取得了相对较好的结果,略低于本文的MIC-TS算法,图4以条状图的形式展示了不同算法在样本数量为2 000、5 000、10 000的实验时的F值和正确边数。另外MIC-TS和TS算法构建网络的指标的对比证明了初始网络的选取会较大程度的影响算法性能,通过MIC构建初始网络,在一定程度上有效地排除了评分搜索阶段中的随机因素的影响,增强了算法的鲁棒性。

图3 MIC-TS算法生成的SACHS网络Fig.3 SACHS network generated by MIC-TS

(a) F值

(b) TP

对于ECOLI网络数据集,因为其属于连续型数据,需要进行预处理才能使用。将得到的数据集进行归一化、标准化,随后进行离散化处理,Yu等[17]研究表明,对于贝叶斯网络,三值离散化方法有较高的准确率和稳定性,因此本文采用“均值-方差”的三值离散化方法对ECOLI数据集进行处理。

设随机变量i在第j个数据样本中的取值为xij,变量i在不同数据样本中表达均值为μi,方差为σi,则对xij有

(11)

离散化后,取值2表示与实验中表达量对比,出现了高水平表达;取值1表示正常水平表达,取值0表示低水平表达,在处理后的ECOLI数据集上进行不同样本量的交叉验证的结果见表4。

表4 MIC-TS与各个算法在ECOLI数据集上的实验结果Tab.4 Experimental results of MIC-TS and various algorithms on ECOLI data set

从表4可以看出, MIC-TS算法在较大的ECOLI网络下相比经典算法也存在优势,在样本数量为2 000、5 000、10 000的实验结果中,F值和TP值都显著高于其他算法,但HD值相比于MMHC和Banjo算法的结果也偏高,图5为MIC-TS算法生成的SACHS基因调控网络图。随着样本数量的增多,MIC-TS算法学习的更加充分,性能的提升幅度也更高。在数据量较少(2 000)时,MIC-TS学习的基因调控网络各项指标与TS,Hill Climbing算法差距不大,推测是因为低数据量时通过最大信息系数构建的初始网络较不准确,生成了标准网络中没有的边所导致,随着数据量的增多(5 000,10 000),MIC-TS的实验指标中的TP值明显增大,生成网络与真实网络更加接近,提升明显。MIC-TS算法的实验结果在HD值上略大于MMHC以及Banjo算法,推测是因为MMHC算法因其仅在筛选后的网络空间内搜索,较为有效的降低了HD值,但同时学习到的正确边也会减少,TP值略小,图6以条状图的形式给出了不同样本量下各个算法在F值以及正确边数(TP)上的数据对比,可以直观地看出,本文的MIC-TS算法的数据相比其他算法更为优秀,随着数据量的增多,学习到的正确边数增长明显。

图5 MIC-TS算法生成的ECOLI网络Fig.5 ECOLI network generated by MIC-TS

(a) F

为了验证本文的MIC-TS算法是否优于其他使用MIC构建初始网络时的评分搜索算法,在上文2个数据集的不同样本量上对本文MIC-TS算法和在MIC初始网络上进行评分搜索的Hill Climbing算法(以下简称MIC-HC)进行实验对比(表5),表中的数据显示在2个不同大小数据集的各个样本量上,MIC-TS的数据都要更优秀,和上文的实验结果对比,证明了MIC-TS算法在评分搜索阶段使用禁忌表跳出局部最优的方式能得到更为优秀的结果,有效提高了算法的性能。

表5 MIC-TS与MIC-HC算法在不同数据集的实验结果Tab.5 Experimental results of MIC-TS and MIC-HC algorithms in different datasets

3 结语

本文将贝叶斯网络的结构学习和最大信息系数MIC结合生成的MIC-TS算法应用于基因调控网络的构建。通过计算网络中各个节点的MIC值,筛出网络中可能性较大的边来构成初始网络结构,进一步使用Tabu搜索和BDe评分函数学习最终的贝叶斯网络结构,有效地提高了算法的性能。经过在2个不同规模的基因调控网络数据上进行实验,并与若干经典算法进行指标上的对比,验证了文中算法的准确性和普适性。如何使用其他算法与MIC构成的初始网络进行结合,充分利用不同算法的优势提高算法的准确性以进行基因调控网络的构建仍需要进行进一步的研究。