随机需求下多危险品定位库存路径问题建模与算法研究

马检, 靳文舟

( 华南理工大学 土木与交通学院, 广东 广州 510641)

0 引言

近年来,我国的危险品物流产业维持了高速增长的态势,但无论是在理论研究还是生产实践上,都仍处于初级阶段,尚有很多待解决的问题。目前学界关于危险品物流方面的研究,如配送中心选址、配送路线优化等,都还停留在理论阶段，没有与生产实际进行进一步的结合。而生产中的各个危险品供应链上的企业各自为政,沿用着传统普通货物的物流系统进行危险品的运输。这种方式不仅不能有效降低物流的成本,还因缺乏安全管理意识和能力而引发危险品泄露、燃烧甚至爆炸的事故。如2018年发生的致22人死亡的石家庄危险品运输车爆炸、2019年发生的江苏响水化工厂爆炸等事故,就是物流中不同环节安全管理不善的直接后果，为群众生命财产安全、政治稳定、社会经济、环境保护等方面都造成了很大的负面影响，因此,危险品物流理论和产业的相关研究日益为管理部门、企业界及学术界所关注。

早期对危险品物流的研究主要集中在配送运输路径优化上,Dantzig等[1]于1959年首先提出,作为车辆调度问题的延伸。目前,对危险品运输的研究普遍已从早年的单目标问题转变为双目标乃至多目标问题,成本、风险、风险公平性[2]、客户满意度[3]等均成为研究中的目标。精确算法[4]、禁忌搜索算法[5]、粒子群算法[6]、多目标遗传算法[7-9]等求解方法也被应用于求解。其中,由于运输路径问题的NP-hard问题特性和遗传算法良好的适用性,启发式算法中的多目标遗传算法应用最为广泛。

在模型上,越来越多的约束条件被加入到研究中，如时间窗[10]、风险公平性[11]、多种类[12]等。朱伟等[3]根据随机需求的概率密度函数,将随机需求转化为一个约束,从而消除了模型的不确定性。风险的表征方面,Toumazis等[13]将在险价值理论应用在危险品风险模型上(CVaR)。代存杰等[14]通过事故发生概率、影响半径和事故发生点的人口计算风险,而考虑了风险分布特征。柴获等[15]将事故发生点和人口聚集点分离开来,并定义冲击系数,使风险大小与两点间欧氏距离有关。上述过往研究中的风险模型距离现实仍有一定距离。

本文将在产地-配送中心-客户三级供应链系统中,从最优库存模型出发,对需求的不确定性进行处理,提出应对一条路线上多客户需求不确定的配送和仓储量公式，并研究危险品风险表征中影响半径和衰减系数的关系,提出计算风险的更为一般化、可实践的方法。最后开发并测试种群结构控制选择算子(PSC),提出适用于其他多目标整数规划问题的改进型算法。

1 模型建立

1.1 问题描述与假设

本文以不确定需求的多种类危险品物流管理的配送中心定位-配送中心及需求点的库存策略制定-配送路线设计为研究对象。每种危险品对应一个产地和若干备选配送中心、客户,而每个产地、配送中心和客户也对应一种危险品,危险品从产地运输到配送中心的过程称补货,从配送中心运输到客户的过程称配送。因为产地和危险品一一对应,配送中心和补货车辆一一对应,所以各用相同符号表示。

优化的双目标为总成本及风险值的最小化。总成本包括配送中心开放成本、危险品的储存成本、订货成本和运输成本,与危险品种类、库存计划、运输路径等有关。总风险考虑的是危险品的爆炸风险,根据危险品储存和运输时发生爆炸的可能性、爆炸强度和衰减特性等来计算,与危险品特性、库存计划、运输路径、车辆速度、人口分布等有关。

决策变量Wm=1时配送中心m开放,否则为0。Xi,k=1时车辆k服务于节点i,否则为0,i,j∈M∪N。Yi,j,k=1时车辆k先后在节点i,j作业,否则为0,i,j∈M∪N。

1.2 配送策略分析

(1)

(2)

令总成本最小,求得客户的订货周期和最优订货批量分别为

(3)

(4)

(5)

取其期望值为车辆k实际的配送周期Pk，即

(6)

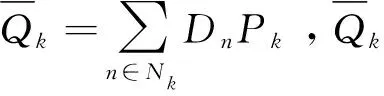
(7)

设置信度α的分位数为zα,上式可写作

(8)

(9)

(10)

(11)

(12)

则总补货运输CR为

(13)

配送中心和客户的平均库存成本CI为

(14)

另外,设每个配送中心的开放成本为cm,则总开放成本为

(15)

1.3 风险模型

定义危险品对平面任意坐标的造成的风险与种类、距离、受影响人口有关。根据(Carotenuto等, 2007),给定危险品坐标(x0,y0),则其影响衰减公式为e-τl[(x-x0)2+(y-y0)2],其中τl为种类l危险品的影响衰减系数。对上式在整个平面上进行二重积分,可求得危险品的全部影响为

(16)

库存风险空间分布如图1所示。若给定一个以险品坐标(x0,y0)为圆心的圆,分布在该圆形区域内的影响大小与全部影响之比大于一定比例β(如99%),则认为影响全部分布在该区域中。此时可求得该圆形区域的半径,即为危险品l的影响半径λl,与影响衰减系数有关。

(17)

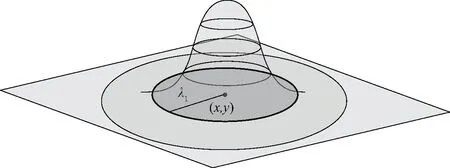
图1 库存风险空间分布示意图Fig.1 Impact distribution of hazmat’s inventory

与库存成本公式相似,配送中心和客户库存总风险RI为

(18)

在运输中,车辆就是图1中钟型风险场的中心,这个风险场随车辆移动,擦过道路旁的某个点(x,y),那么点(x,y)的风险为随时间变化的曲线,与风险空间分布的钟型的竖直截面具有相同形状。运输风险模型的构建如图2所示，运输风险的形成如图2(a)所示。

e-τl(d2+z2)= e-τl(d2+v2t2)。

(19)

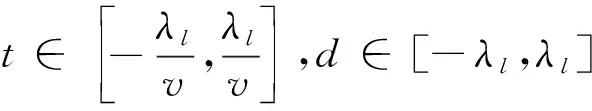
(20)

(21)

补货运输风险为:(l既表示危险品种类,也表示产地节点)

(22)

模型为

min(CD+CR+CI+CL),

(23)

min(RD+RR+RI),

(24)

s.t.

(37)

式(22)表示总成本最小化,式(24)表示总风险最小化,式(25)表示每种危险品至少开放一个配送中心,式(26)表示未开放的配送中心没有车辆,开放的配送中心至少有1台车辆，式(27)、(28)表示出发的车辆至少经过一个配送中心和一个客户，式(29)表示每个客户都有车辆服务，式(30)表示每个客户只被服务一次,且车辆形成闭合回路，式(31)表示同一车辆的配送中心和客户危险品种类相同，式(32)、(33)、(34)分别是配送中心、客户和车辆容量约束，式(35)、(36)、(37)为决策变量。

2 算法与算例分析

2.1 编码、杂交和变异方法

首先采用NSGA-Ⅱ算法,即带有精英选择策略的非支配排序多目标遗传算法(non-dominated sorting genetic algorithm-Ⅱ，NSGA-Ⅱ),尝试求解该问题。

编码方式:将所有配送车辆路线排列成2行矩阵,第1行为车辆经过的节点编号,第2行为该节点所属的危险品种类。每辆车的起终点均为配送中心,在个体矩阵中出现的配送中心则说明已启用,未出现则说明不启用。

杂交方式:

步骤①:将个体1所有客户序列提取出来,每种危险品保留前一半序列,得到半成品序列。

步骤②:剔除个体2中半成品序列已出现过的客户,分种类将个体2剩余客户依次填入半成品的后半段。

步骤③:将合成的新序列回填个体1空位,得到新的子代1。

编码及杂交方式演示如图3所示。

图3 编码及杂交方式演示Fig.3 Coding and crossover operator

变异方式1:随机选择同一车辆配送的2个客户,互换位置；

变异方式2:随机选择一个客户,移到另一辆同类车辆路线上；

变异方式3:随机取消一辆车,所服务的客户移到其他同类车辆路线上(如果配送中心上只有这一辆车,则关闭这个配送中心)；

变异方式4:随机选择一个配送中心生成一辆车,从其他同类车辆中随机抽取客户。

2.2 求解效果与分析

创建一个3类危险品-每种危险品3个候选配送中心-共30客户的算例,其路网及节点性质如图4所示:

图4 算例路网Fig.4 Road network of the example

运用NSGA-Ⅱ算法求解该算例,种群规模为200,迭代200次,迭代过程及结果如图5所示。

其中,一个非支配等级中互不相同的个体数量称为该等级的有效规模。可以看出,随着迭代的进行,最高等级规模迅速增大,到70次迭代时已基本占据整个种群,同时最高等级的有效规模的增长也骤然减慢,风险和成本的降低趋于平缓,可以认为算法已达到收敛。此后虽有优化,但非常缓慢。最终等级1的规模为200,而Pareto解集的规模仅为30。

在传统NSGA-Ⅱ中,父代和杂交变异产生的子代会进行合并,合并种群根据非支配等级和拥挤度进行排序,排名在预设种群规模以内的个体都会被选中,组成新一代种群。假设父代中的一个最高等级个体(称个体1)经过杂交变异后,仍存在于子代中,那么个体1就会在合并种群中出现2次,而精英选择会将这2个相同的个体1都保留下来。这种情况的连续出现会让个体1数量指数增大,而更多的相同个体1意味着下一代中出现个体1的概率越大——2个个体1杂交后仍是个体1。这种数量和出现概率的互相促进,会让个体1在短时间内大量复制,占据大量空间,排挤掉低等级的个体。显然,在图5(a)中,这种最高等级规模急速增长的现象出现了数次。

这种现象有利有弊：一方面,加速了算法的收敛；另一方面,仅靠少量重复的优秀个体进行杂交变异,此后算法对解空间的探索能力也会大大下降。

这种现象在用整数规划模型研究的多目标实际问题中影响更大。非整数规划通常有无穷多解,杂交变异后的子代中,出现与父代相同个体的概率很低。而整数规划中可行解的总数可能是很有限的。并且,在对实际问题的研究中,研究者要根据问题来设计个体的编码、解码及种群的初始化、变异和遗传,特别是在种群初始化时,常常不能保证对潜在解空间的覆盖程度,进一步减少了算法实际运行时可行解的总数,导致算法在合并种群和精英选择的作用下提前收敛。

对此,很有必要将种群中各等级个体的数量控制在合理的范围内,控制该现象,才能平衡算法收敛速度和对解空间的覆盖度。基于此,本文提出带种群结构控制的非支配排序遗传算法(non-dominated sorting genetic algorithm-Ⅱ with population structure control， NSGA-Ⅱ-PSC),在第三节中阐述。

3 基于种群结构控制的选择策略改进

3.1 选择算子模型

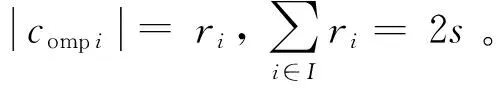
(38)

(39)

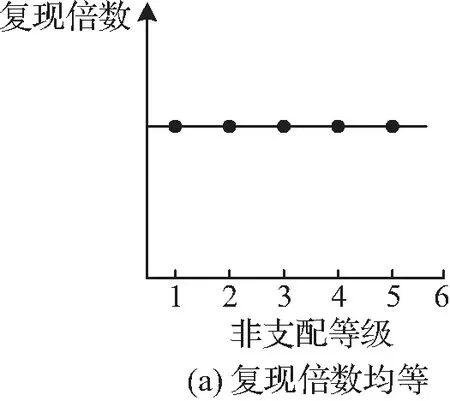
通过对各等级的复现倍数μi进行控制,就可以合理地规划种群等级结构,将各等级规模控制在合理的范围内。如图6所示,本文设置复现倍数均等、线性递减和负指数递减3种带种群结构控制的选择模型,以进行种群结构的控制,并观察算法的表现:

3.2 模型表达式及其参数

① 复现倍数均等(NSGA-Ⅱ-PSC-Ⅰ)

在复现倍数均等的种群结构中,所有非支配等级的复现倍数相同,所以μi表达式中仅有一个常数a作为参数，因此,均等复现倍数模型为

μi=a,∀i∈I。

(40)

该常数的表达式为

(41)

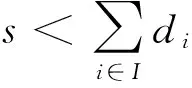
② 复现倍数线性递减(NSGA-Ⅱ-PSC-Ⅱ)

设复现倍数线性递减的模型为

μi=ai+b,∀i∈I,a<0。

(42)

(43)

③ 复现倍数负指数递减(NSGA-Ⅱ-PSC-Ⅲ)

设复现倍数负指数递减的模型为

μi=ba-i,a>1,b>0。

(44)

I中元素最小值为1,设其最大值Imax=j,前四分之一分位数l=(1+j)/4,中值k=(1+j)/2。

(45)

(46)

3种模型的计算流程如图7所示。

图7 3种模型的计算流程Fig.7 Flow chart of three models

3.3 PSC选择流程

在实际计算中,根据2.2中模型求得的μi可能仍不满足约束(39)，而且s和ui都应该是整数,但μi往往不是整数。为解决这2个问题,采用以下步骤进行进一步的修整。

图8 NSGA-Ⅱ-PSC流程图 Fig.8 Flow chart of NSGA-Ⅱ-PSC

步骤1：i=1,根据上述流程计算μi的值。

步骤2：对μi向下取整得到[μi],使reffi复制[μi]次得到集合rseqi；

步骤3：对di(μi-[μi])向上取整得到[di(μi-[μi])],取qeffi中拥挤度最大的[di(μi-[μi])]个体,得到补充集合rsupi；

步骤4：步骤2和步骤3的集合相加得到新的等级i个体集合rnewi=rseqi+rsupi；

步骤6：新种群的规模为s′=|pnew|,此时有s′≥s。根据非支配等级和拥挤度,在pnew中选出最优的s个个体组成最终种群psel。

NSGA-Ⅱ-PSC的总体流程及其中的PSC选择流程如图8所示。

3.4 模型效果对比

设计随机路网并给定各节点的供应链相关参数,分别应用带传统快速非支配选择算子和3种种群结构控制选择算子的NSGA-Ⅱ进行模型求解。种群规模设定为100,迭代次数设定为150次。

路网规模分3种,具体如下:

3*:3类危险品-每种危险品3个候选配送中心共30个客户；

4*:4类危险品-每种危险品4个候选配送中心共40个客户；

5*:5类危险品-每种危险品5个候选配送中心共50个客户。

4种算法在3* 规模下,种群规模200和150次迭代的某次求解的迭代过程如图9所示。

由于每个路网参数不一,因此为了方便比较,将所有结果进行归一化处理，将经典NSGA-Ⅱ求得的Pareto最优解集中各指标值调整为设定值,其他值调整为其实际值与NSGA-Ⅱ实际值之比乘以NSGA-Ⅱ设定值。各设定值见表1。

表1 归一化处理中的设定值Tab.1 Set values in normalization processing

将种群规模设定为100,迭代次数设定为150次,并分别记录其第50、100、150次迭代时的目标函数最小值。每种路网规模随机生成10个路网,每个路网重复求解10次,详细的求解综合对比见表2。

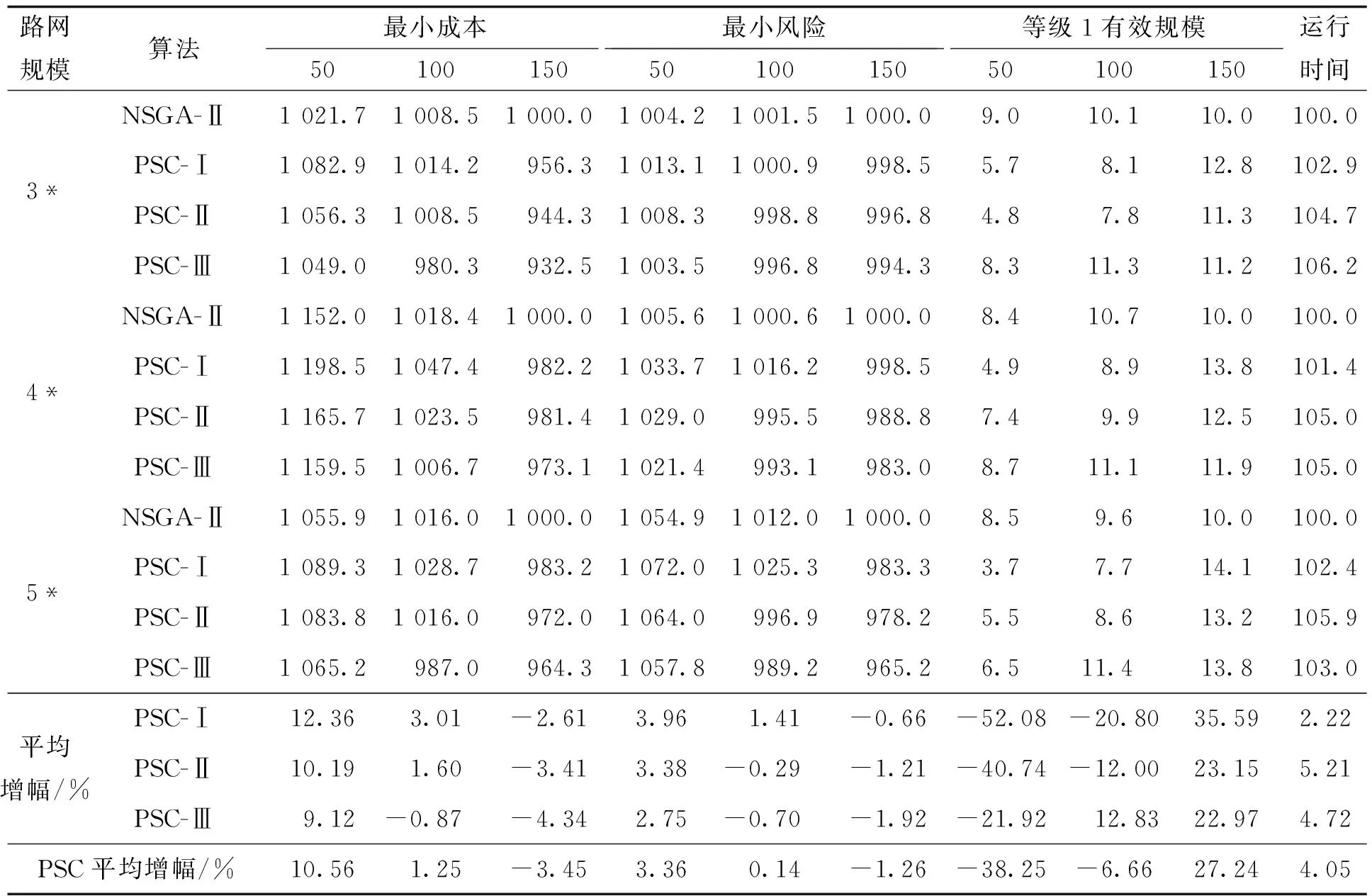
表2 不同迭代次数下4种算法性能比较Tab.2 Comparison of four algorithms under different iterations

可以看出,带PSC算子的NSGA-Ⅱ比传统NSGA-Ⅱ初期收敛较慢,在50次迭代时,PSC算子的最小成本和风险平均比传统NSGA-Ⅱ高10.56%和3.36%,等级1有效规模低38.25%。而从相对传统NSGA-Ⅱ的平均增幅看,在PSC算法中,收敛最慢的是PSC-Ⅰ,最快的是PSC-Ⅲ。150次迭代时,PSC算子的表现则明显反超传统NSGA-Ⅱ选择算子,成本和风险平均比传统NSGA-Ⅱ低3.45%和1.26%,Pareto解集规模则高出27.24%。

其中,在目标函数最小化上表现最优的是PSC-Ⅲ算子,2个目标函数平均比传统NSGA-Ⅱ低4.34%和1.92%。而在Pareto解集规模上表现最好的是PSC-Ⅰ,平均比传统NSGA-Ⅱ高了35.59%,PSC-Ⅱ和PSC-Ⅲ则相差不多。

另外可以看出,随着算例规模的增大,也就是问题的复杂化,PSC算子在Pareto解集规模上的优势越明显,相比传统NSGA-Ⅱ能得到更多的Pareto最优解。

这是由于,在种群结构上,高等级解占比由大到小分别是传统NSGA-Ⅱ、PSC-Ⅲ、PSC-Ⅱ、PSC-Ⅰ。高等级占比大的种群结构能够加速算法的收敛,而等级占比小的种群结构能让算法探索更大的解空间。在问题太复杂时,收敛速度快的算法更有效率,而随着问题变复杂,对解空间探索更为充分的算法往往能获得更好的解集，因此,对种群结构施加控制是提高遗传算法质量的一种思路。

最后,在运行时间上,PSC算法平均只多出4.05%,在可接受的范围内。

根据上述分析,平衡收敛速度和解集质量,采用NSGA-Ⅱ-PSC-Ⅲ算法重新求解2.2节图4的3*算例,图10为求得的Pareto最优解集。Pareto解集规模为44,比NSGA-Ⅱ提高46.7%,最低成本解的成本和风险值分别为1 975.08和4 015.19,比NSGA-Ⅱ分别降低了4.64%和1.20%；最低风险值的成本和风险值分别为3 373.04和2 434.34,比NSGA-Ⅱ分别降低了2.31%和0.89%。图11为Pareto解集中最低成本解、最低风险解分别的运输路线。

最低成本解共有3台配送车辆,平均行驶里程为508.39 km,总里程为1525.16 km；最低风险解共有5台配送车辆,平均行驶里程为363.41 km,总里程为1 817.08 km；运输车辆的增加不仅减少了单台车辆的装载量,降低了驾驶员的风险,而且使得风险得以分散化分布,也提高了整个区域的风险公平性。

图10 Pareto最优解集Fig.10 Pareto optimal set

4 结语

本文结合需求不确定性与库存理论,构建了危险品定位库存路径模型,并提出了基于风险分布特性和人口分布特性的风险模型。此外,本文设计了能一次性求解LRP问题的算法,并在传统NSGA-Ⅱ的基础上提出了NSGA-Ⅱ-PSC及其3种类型。算例表明,对种群结构进行控制能够影响NSGA-Ⅱ的性能,NSGA-Ⅱ-PSC在解集质量上明显优于传统NSGA-Ⅱ,且在复杂问题上优势更明显，其中,PSC-Ⅰ能获得最好的解集质量,而PSC-Ⅲ的收敛速度最快。