凸面恒温基底上固着液滴蒸发特性研究

张舒蕾，李冰杰，蒋健，董新宇，2，刘璐，2

（1 华北电力大学动力工程系，河北 保定 071003； 2华北电力大学，河北省低碳高效发电技术重点实验室，河北 保定 071003）

引 言

固体基底上固着液滴的蒸发广泛应用于化工[1-2]、喷淋冷却[3-4]、电子器件散热[5-6]等领域。液滴蒸发过程包含的传热传质机制有：基底内部导热、液滴内部由于温度梯度和表面张力梯度而产生的对流、液滴与基底间界面换热、液滴周围蒸气的传质扩散，以及蒸发引起的气液界面演化[7]。其中，需要考虑的问题涉及三相接触线动力学、界面演化、液滴内部Marangoni流动等。

近年来，对固着液滴蒸发过程的研究多集中于工质种类[8-9]、基底性质[10-11]及外界环境[12-15]等因素对液滴蒸发特性的影响，主要分为实验研究和理论研究两个方面。实验研究方面，Rowan等[8]实验研究发现，聚甲基丙烯酸甲酯表面上水滴和特氟龙表面上的醇类液滴蒸发过程的高度和接触角均随时间线性变化，当初始接触角小于90°时，蒸发初始阶段为恒定接触半径蒸发模式。闫鑫等[9]研究了金纳米流体液滴的蒸发模式，发现纳米粒子在接触线上的沉淀导致接触线钉扎，蒸发过程中接触角不断减小。金艳艳等[10]选用单晶硅片和聚四氟乙烯膜作为基底，采用四种浓度的乙醇水溶液，研究了水-乙醇二元混合液滴在固体表面上的蒸发规律。实验结果表明，添加乙醇缩短了液滴的蒸发时间，减弱了液滴的钉扎效应，使得液滴更容易发生滑移。Gurrala等[11]实验研究了不同基底温度下乙醇-水二元混合物固着液滴的蒸发特性，发现提高基底温度会迅速降低液滴寿命。Liu 等[15]进行了降压过程中固着水滴蒸发的实验和理论研究，结果表明，由于基底的润湿性不同，水滴在载玻片表面蒸发最快，在特氟龙表面蒸发最慢。理论研究方面，董佰扬等[16]通过引入动态接触角模型模拟液滴蒸发过程，分析了液滴体积和接触角随时间的变化。Nguyen等[17]采用分离变量法求解了液滴蒸发准稳态传热扩散与传质扩散的双向耦合模型，提出了固着液滴蒸发与界面蒸发冷却效应耦合的解析解。Zhu 等[18]建立了恒定接触角蒸发模式下固着液滴的三维蒸发模型，该模型可直接通过局部蒸发通量计算液滴界面演化。Shen等[19]对固着液滴蒸发过程进行了理论分析和数值模拟，研究了接触角、蒸发冷却效应和基底过热对液滴蒸发的影响。

尽管学者们对固着液滴蒸发过程开展了大量研究，但大多集中于水平刚性基底上的液滴蒸发现象，而对于固着液滴在曲面基底上的研究则较少涉及。液滴在曲面基底上的蒸发现象在工业生产中非常常见，例如：液滴撞击加热管壁的汽化过程、内燃机燃料液滴撞击弯曲壁面的汽化过程等[20]。对于曲面基底，基底导热[21]、液滴周围蒸气扩散[22-24]和界面演化[25-28]对液滴蒸发的影响与平面基底存在差异。Dhar等[21]研究了超疏水表面上的固着液滴蒸发过程中其内部流动速度与基底表面曲率的关系，发现增加基底曲率可以提高液滴内部流速。Paul 等[24]研究了固着液滴在亲水和超疏水弯曲表面上的蒸发过程，利用粒子图像测速技术获得了蒸发液滴内部的流场，并分析了弯曲基底上液滴蒸发的形态变化。Petsi等[26]研究了在弯曲和水平恒温基底上的二维固着液滴蒸发过程其内部温度分布，发现液滴在凸面基底上的温度变化大于在水平和凹面基底上的温度变化。Shen等[27]建立了固着液滴在弯曲基底上蒸发的传热传质理论模型，采用环形坐标系将蒸发传质与气/液界面传热和固/液界面传热三者耦合，分析了蒸发冷却效应、基底热导率和液滴初始形状对蒸发过程的影响。

针对曲面基底上液滴蒸发特性的研究还较少，且对于凸面恒温基底上液滴蒸发传热传质理论模型缺乏实验验证。本文搭建凸面恒温基底上蒸馏水液滴蒸发的可视化实验系统，研究液滴蒸发模式，采用红外热像仪捕获液滴表面温度分布。采用环形坐标系建立凸面恒温基底上固着液滴蒸发的传热传质模型，在Shen 等[27]研究的基础上，理论推导液滴内部温度分布以及周围蒸气浓度分布的解析解。将模型计算结果与实验结果对比，验证模型的可靠性。

1 实验系统

本文搭建了凸面恒温基底上固着液滴蒸发的可视化实验系统，如图1所示。该系统由加热模块、温度控制模块以及图像采集模块组成。加热模块包括不同曲率直径的铜圆柱（D0=20、30、40 mm）和加热棒（额定功率80 W）；温度控制模块包括PID 温度控制器和热电偶，用于控制基底表面温度，其中PID 温度控制器精度为0.1℃，热电偶的绝对测量误差为±0.2℃；图像采集模块包括CMOS 相机、红外热成像仪和冷光源。

其中，CMOS 相机（Point Grey，分辨率1280×960，帧率90 帧/秒）记录液滴蒸发过程中的形态演变，红外热成像仪（FLIR T620，绝对测量误差±2℃，帧率60 帧/秒）记录液滴表面温度分布。为确保红外热像仪捕获温度的准确性，在加热铜柱表面贴一层厚度为10 μm 的亲水性黑膜（Nitto UTD-10B），黑膜表面粗糙度Ra= 0.023 μm。实验中，在铜柱侧面做好中心位置标定，使用ImageJ 软件对图像进行分析处理，测量误差为0.026 mm。实验采用蒸馏水作为液滴工质，初始体积为1、3 和5 μl，基底温度分别为62.6、72.6、82.6℃，环境温度为（26.3±0.2）℃，相对湿度为52%±3%。实验过程中，通过恒温恒湿空调调节实验室内温湿度恒定，尽可能减小环境因素变化对实验过程的影响。每组工况实验重复3 次，保证实验的可重复性。

2 理论模型

对于曲面基底，引入圆环坐标系(α,β)以描述液滴蒸发过程的界面演化，如图2 所示。液滴/基底界面和液滴/空气界面分别由（0 ≤α＜∞,π -θsub）和（0 ≤α＜∞,π -θ）进行描述。其中，θ和θsub分别为液滴球冠、基底球冠与水平面在接触线上的夹角；R为液滴接触半径；T∞和C∞分别为无穷远处环境温度和蒸气浓度；Tw为基底表面温度；iα和iβ分别为沿α轴和β轴方向的单位向量。

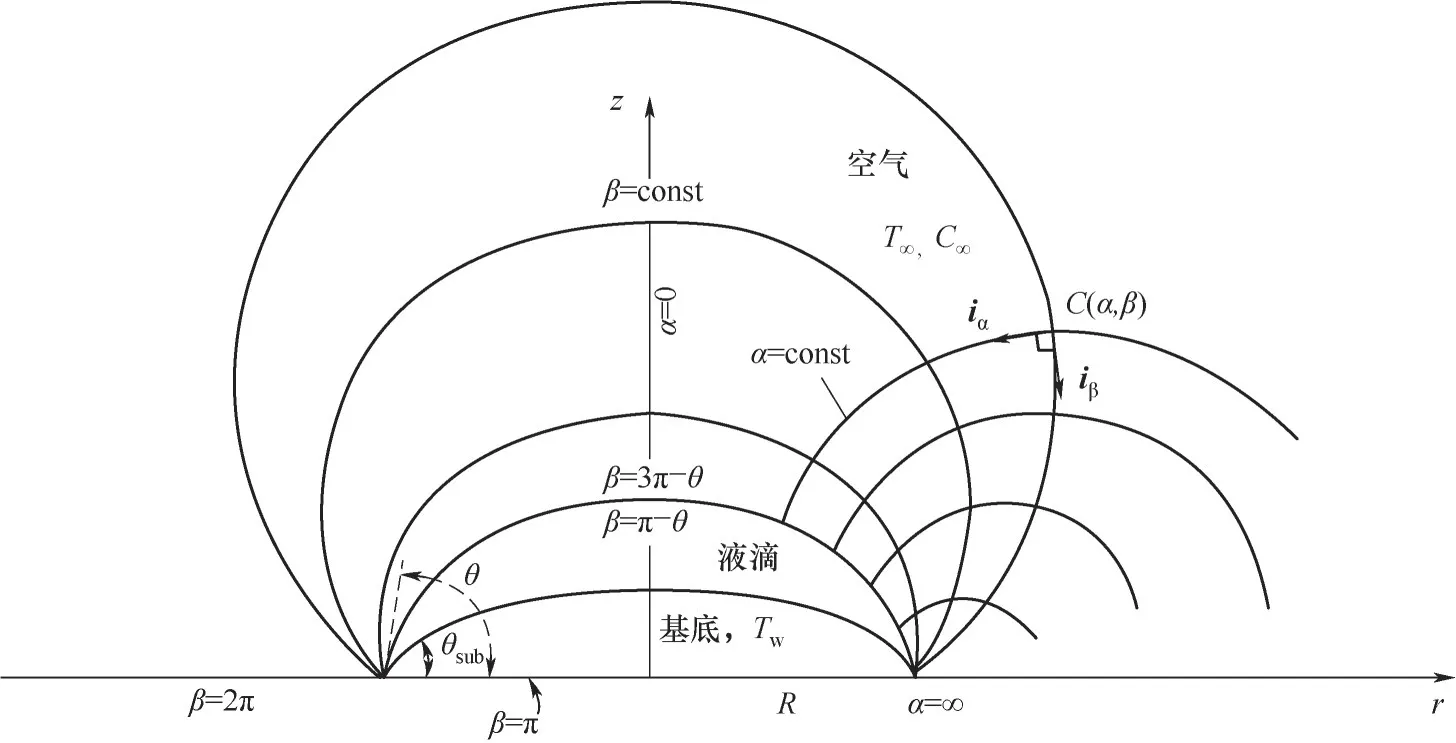
图2 物理模型示意图[27]Fig.2 Schematic diagram of physical model[27]

边界条件为：

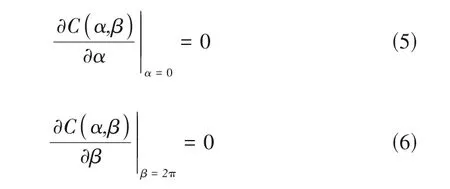
传热与传质耦合的边界条件为：

式中，q为热通量；L为液滴的汽化潜热；J为液滴/空气界面处的蒸发通量。

对上述方程进行求解可得[27]：

式中，E0为蒸发冷却数（E0=bLD/k），b= dCsat/dT，k为液滴热导率，D为蒸气在空气中的扩散系数[29]。当E0= 0时，不考虑蒸发冷却效应。

液滴的质量蒸发率为：

其中

3 结果与分析

3.1 实验结果

3.1.1 液滴形态变化 图3 所示为基底温度为72.6℃时5 μl 固着水滴在凸面基底上蒸发过程的形态变化，图4 为凸面基底上不同初始体积的液滴接触半径随蒸发时间的变化。

图3 凸面基底上固着水滴蒸发过程的形态演化（V0 = 5 μl，Tw = 72.6℃，D0 = 40 mm）Fig.3 Morphological evolution of sessile water droplet evaporation on convex substrate(V0 = 5 μl，Tw = 72.6℃，D0 = 40 mm)

图4 凸面基底上不同初始体积固着水滴蒸发过程接触半径随时间的变化（Tw = 72.6℃，D0 = 40 mm）Fig.4 Variation of contact radius with time during sessile water droplet evaporation with different initial volumes on convex substrate(Tw = 72.6℃，D0 = 40 mm)

分析图3、图4 可得：水滴在凸面基底上蒸发分为三个阶段，即铺展阶段、恒定接触半径蒸发阶段和混合蒸发阶段。铺展阶段指液滴在基底上铺展直至最大接触半径，当液滴体积分别为1、3、5 μl时，其最大铺展半径分别为0.71、1.46、2.05 mm，铺展阶段占总蒸发时间的比例为4.3%、3.2%、2.8%。恒定接触半径蒸发阶段指液滴在蒸发过程中接触半径保持不变而接触角不断减小，当液滴体积分别为1、3、5 μl 时，该阶段占液滴总蒸发时间比例分别为89.3%、92.5%、93.7%。混合蒸发阶段指液滴接触半径和接触角均随时间不断减小，液滴接触线开始“去钉扎”，当液滴体积分别为1、3、5 μl时，混合蒸发阶段占总蒸发时间的比例为6.4%、4.3%、3.5%。综合来看，凸面恒温基底上蒸馏水液滴的蒸发主要遵循恒定接触半径蒸发模式。

为对比凸面与平面基底上液滴蒸发的区别，进行基底温度为72.6℃时5 μl固着水滴在平面基底上的蒸发实验。图5所示为液滴蒸发过程中的形态变化，图6 为两种不同基底表面上液滴蒸发过程的接触半径随时间的变化。可以看出，平面基底上的水滴铺展后，进入恒定接触半径蒸发阶段，其后接触线缓慢收缩，蒸发后期接触线快速收缩直至液滴完全蒸发。相较于凸面基底，平面基底上的液滴最大铺展半径较小，钉扎时间缩短，总蒸发时间较长。这是由于基底表面曲率的存在促进了液滴的铺展，同时延缓了接触线收缩行为的发生。凸面基底上液滴的铺展面积较大，增强了基底向气液界面的传热，提高了液滴的蒸发速率。

图5 平面基底上固着水滴蒸发过程的形态演化（V0 = 5 μl，Tw = 72.6℃）Fig.5 Morphological evolution of evaporation process of sessile water droplet on flat substrate(V0 = 5 μl，Tw = 72.6℃)

图6 不同基底表面上固着水滴蒸发过程接触半径随时间的变化（V0 = 5 μl，Tw = 72.6℃）Fig.6 Variation of contact radius with time during water droplet evaporation on different substrate surfaces(V0 = 5 μl，Tw = 72.6℃)

3.1.2 液滴表面温度分布 图7所示为凸面基底温度72.6℃时，5 μl 蒸馏水液滴蒸发过程的红外热成像图。蒸馏水在红外热像仪的工作波段下发射率为0.96，接近1[30]，故可认为红外热像仪所测温度为液滴表面温度。从图中可以看出，当液滴铺展到最大半径后，液滴表面沿径向有较大温度梯度，沿液滴表面从中心到接触线方向温度单调递增，液滴表面中心温度最低。由于液滴蒸发冷却作用，接触线附近基底温度明显低于周围基底温度。随后，液滴内部整体温度升高，径向温度梯度减小，接触线附近基底温度与周围基底温度差值减小。这是由于液滴接触角减小，液滴气液界面与基底表面之间的距离减小，从而促进了从基底到气液界面的传热，造成液滴温度升高，表面整体温度趋于均匀。当进行到蒸发后期，液滴整体表面温度分布均匀，接触线附近基底温度接近周围基底温度。

图7 凸面基底上固着水滴蒸发过程的红外热成像图（V0 = 5 μl，Tw = 72.6℃，D0 = 40 mm）Fig.7 Infrared thermography of evaporation process of water droplets on convex substrate(V0 = 5 μl，Tw = 72.6℃，D0 = 40 mm)

3.2 模型计算结果

3.2.1 影响液滴蒸发速率的因素 使用Matlab 软件对理论模型进行计算，图8对不同液滴初始体积、凸面基底温度及凸面基底曲率下液滴蒸发体积变化的模型计算值与实验结果进行了比较。图中，将液滴体积无量纲化处理，V为液滴剩余体积，V0为液滴初始体积。

图8（a）比较了液滴初始体积对液滴蒸发过程的影响。可以看出，当不考虑蒸发冷却效应即E0= 0时，液滴体积变化速率较实验结果更快，液滴蒸发时间更短，这与Xu 等[31]的理论分析结果相一致，表明模型考虑蒸发冷却效应可使计算结果更加准确。

图8（b）比较了凸面基底温度对液滴蒸发过程的影响。根据计算，当基底温度为62.6、72.6、82.6℃时，蒸发冷却数E0的取值分别为0.52、0.72、0.95。如图所示，随着基底温度的升高，液滴的蒸发速率加快。这是由于基底温度越高，气液界面温度也越高，液滴蒸气浓度越大，蒸发速率越快。

图8 模型计算值与实验值的比较Fig.8 Comparison between calculated results and experimental data

图8（c）比较了凸面基底曲率对液滴蒸发过程的影响。可以看出，当基底曲率直径D0= 20 mm时，液滴蒸发速率最快。这是由于基底曲率直径越小，液滴重力沿基底切向的分力越大，使得液滴在凸面上的铺展半径更大，基底向气液界面的传热增强，加快了液滴的蒸发。

由图8 可以看出，模型计算值与实验结果吻合较好，验证了本文模型的可靠性。

3.2.2 液滴内部温度分布 图9所示为凸面基底上液滴蒸发过程的内部温度分布。由于本文模型不考虑液滴铺展过程，故模型计算的初始时刻为液滴铺展到最大接触半径的时刻。图中t͂为无量纲蒸发时间。可以看出，由于液滴/基底界面与液滴/空气界面之间的距离沿径向递减，导致液滴径向产生较大温度梯度，且温度从液滴中心向接触线方向递增。此外，由于液滴沿高度方向距离越大，气液界面与基底间的热阻就越大，基底热量无法迅速传递至液滴顶部[27]，液滴内部沿高度方向产生较大温度梯度，从接触线到液滴顶部温度逐渐减小，最低温度位于液滴顶部中心位置。随着蒸发不断进行，液滴厚度减小，固液接触角逐渐减小，加快了基底与液滴间的传热，使得液滴内部温度梯度减小，整体温度分布趋于均匀，最终接近基底表面温度。

图9 模型计算液滴内部温度分布（V0 = 5 μl，Tw = 72.6℃，D0 = 40 mm）Fig.9 Temperature distribution of droplet evaporation calculated by the model(V0 = 5 μl，Tw = 72.6℃，D0 = 40 mm)

图10 对比了不同曲率直径基底表面上液滴气液界面过余温度的模型计算值与实验结果。可以看出，当凸面曲率直径D0= 20 mm 时，液滴顶部中心温度更高，且液滴的径向温度梯度更小。这是由于液滴铺展半径的增大缩短了液滴气液界面到基底的距离，增强了基底向气液界面的传热，使得气液界面温度分布更为均匀。此外，液滴气液界面处的过余温度沿液滴表面从中心到接触线方向单调递增。随着蒸发过程的进行，液滴体积逐渐减小，液滴内部整体温度趋于均匀。

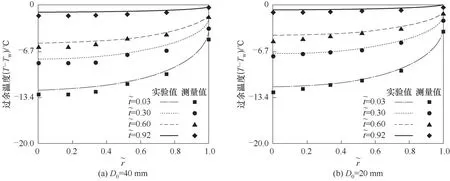
图10 不同曲率直径基底上液滴气液界面过余温度计算值与实验值的对比（V0 = 5 μl，Tw = 72.6℃）Fig.10 Comparison between calculated and experimental values of excess temperature of liquid droplet gas-liquid interface on substrates with different curvature diameters(V0 = 5 μl，Tw = 72.6℃)

4 结 论

本文搭建了凸面恒温基底上的蒸馏水液滴蒸发可视化实验系统，捕获了液滴蒸发过程形态变化和液滴表面温度分布。基于环形坐标系建立了凸面恒温基底上固着液滴蒸发的传热传质模型，推导出液滴内部温度分布及其周围蒸气浓度分布的解析解。将实验数据与模型结果进行对比，验证了模型计算的可靠性。分析了凸面恒温基底上蒸馏水液滴的蒸发特性，得到如下结论。

（1）模型计算中，需考虑蒸发冷却，使模型计算结果与实验值吻合较好。同时，提高基底温度和减小基底曲率直径均可加快液滴蒸发速率。

（2）相较于平面基底，凸面基底上液滴的铺展半径更大，钉扎时间延长，总蒸发时间减小，液滴蒸发主要遵循恒定接触半径蒸发模式。

（3）凸面基底曲率直径越小，液滴蒸发过程内部径向温度梯度越小。这是由于液滴铺展半径的增大缩短了液滴气液界面到基底的距离，增强了基底向气液界面的传热，使得气液界面温度分布更为均匀。液滴气液界面过余温度从中心到接触线方向单调递增。随着蒸发过程的进行，液滴整体温度分布趋于均匀。

符 号 说 明

Ce——接触线处液滴的饱和蒸气浓度，mol/L

C∞——无穷远处环境中的蒸气浓度，mol/L

D——蒸气在空气中的扩散系数，m2/s

D0——凸面基底曲率直径，mm

E0——蒸发冷却数

iα(iβ)——沿α(β)轴方向的单位向量

J——液滴/空气界面处的蒸发通量，kg/(m2·s)

k——液滴热导率，W/(m·K)

L——液滴汽化潜热，kJ/kg

dm/dt——质量蒸发率，kg/s

q——热通量，W/m2

R——三相接触线接触半径，mm

Tw——基底上表面温度，K

T∞——无穷远处环境中的温度，K

T(α,β)——液滴内部温度值，K

V——液滴体积，mm3

θ——液滴球冠与水平面在接触线上的夹角，rad

θsub——基底球冠与水平面在接触线上的夹角，rad

下角标

sub——基底

w——壁面