浮环密封端面分形磨损预估模型及数值分析

张志敏，丁雪兴，张兰霞，力宁，司佳鑫

（1 兰州理工大学石油化工学院，甘肃 兰州 730050； 2 青海民族大学土木与交通工程学院，青海 西宁810007；3 中国航发湖南动力机械研究所，湖南 株洲 412002）

引 言

航空发动机是衡量一个国家军事力量、制造业水平及综合国力的重要指标[1]。随着航空发动机技术的不断进步，航空发动机的密封问题已成为影响其性能及寿命的重要因素[2]。浮环气膜密封是一种非接触式密封，因结构紧凑、轴向尺寸小、质量轻及安全性高等优点[3-4]，常用于航空发动机级间、轴间及轴承腔等关键部位[5]。随着航空发动机性能的不断提升，浮环密封的工况愈加恶劣，其中浮环密封径向间隙动压不足引起的孔柱面碰磨[6-7]和浮环径向振动引起的端面磨损是导致密封失效的两个主要因素。

对于孔柱面碰磨问题，国内外学者对气膜流场进行理论及模拟研究，以提高浮升力，降低孔柱面碰磨失效概率[8-10]。但对于浮环密封端面磨损理论研究鲜有报道，目前仅有关于机械密封磨损预估模型的相关报道。Zhou 等[11-12]首次将分形接触理论和Archard磨损理论结合，提出机械接触面磨损分形模型，为研究密封面磨损问题提供新思路；房桂芳等[13]基于M-B 接触分形模型，通过计算接触面微凸体的变形体积，结合Archard磨损理论建立机械密封面黏着磨损分形模型；魏龙等[14-15]基于Archard 磨损理论及M-B分形模型，建立密封端面磨损分形模型，发现密封端面形貌对磨损特性有较大影响；Kim等[16]使用响应面法(RSM)建立石墨密封环磨损率数学模型，分析了载荷、滑动速度和温度对于石墨磨损率的影响规律；李小彭等[17]结合分形接触理论和塑性变形理论，推导出密封面磨损预测模型，并讨论各参数对于磨损率的影响；惠玉祥等[18]针对油润滑接触式窄端面密封，利用Archard磨损理论，建立考虑接触面磨损的密封性能分析模型。综上所述，目前没有应用于浮环密封端面磨损的相关分形模型，应用于机械密封面的磨损分形模型大部分基于M-B 模型构建，微凸体弹塑性变形阶段、微凸体多尺度性及密封面摩擦因数变化对于磨损率的影响均没有考虑。

针对以上问题，基于分形接触理论和Archard磨损理论，考虑浮环密封端面微凸体弹塑性变形阶段、微凸体多尺度性及变摩擦因数三个因素，提出一种应用于航空发动机浮环密封端面的分形磨损预估模型，探寻浮环密封端面表面形貌参数和运行工况对于磨损率的影响规律，以期对航空发动机石墨浮环的设计、材料选择及工况优化提供一定的理论支撑。

1 浮环密封结构及工作原理

浮环密封主要由石墨浮环、挡圈、波形弹簧、垫片及壳体组成，如图1 所示。其中浮环由钢圈和石墨环镶装而成，工作前石墨浮环由于自重与主轴跑道外壁贴合，此时石墨浮环圆心与轴圆心存在最大偏心距。当工作时，密封气体动压效应使浮环沿径向浮动，并与主轴跑道之间形成刚性流体膜，形成主密封面，阻止气体由高压侧向低压侧泄漏。同时，波形弹簧及高压侧气体将浮环端面压紧于壳体上形成次密封面，防止高压侧气体沿着径向泄漏。

图1 石墨浮环密封结构示意图Fig.1 Schematic diagram of graphite floating ring seal structure

浮环工作过程中由于偏心距会一直变化，导致浮环沿着径向方向存在高频的上下浮动，造成浮环端面与壳体进行对磨产生磨损，由于浮环端面在高速运转下泄漏量很小，可忽略不计，所以浮环端面属于干摩擦。干摩擦运动产生的磨损不仅会改变石墨浮环端面的形状，还会引起应力集中，形成微观裂纹，导致次密封面泄漏量增大，发动机效率下降，严重时会引发重大事故，因此本文重点研究浮环密封装置次密封面磨损问题。

2 浮环密封端面磨损分形预估模型的建立

2.1 基本假设

采用表面形貌仪提取的石墨材料磨损后表面形貌如图2 所示，采用结构函数法可求得石墨材料的分形维数D及特征尺度G，该结果表明，磨损后石墨表面轮廓均具有各向同性的分形特征[14]，因此采用Majumdar 等[19]提出的W-M 分形函数来描述石墨浮环密封端面磨损后的轮廓曲线，表达式如式(1)所示。

图2 石墨浮环表面采样图Fig.2 Surface sampling diagram of graphite floating ring

式中，Z(x)表示密封面轮廓曲线的高度；D表示轮廓曲线的分形维数（对于连续二维表面，1＜D＜2）；G表示轮廓曲线的特征尺度；γ表示剖面的最低截止频率（一般取γ= 1.5）；γn表示随机轮廓的空间频率。

根据上述分析及相关研究成果[13-15,17]，建立浮环密封端面磨损分形预估模型时做以下假设：（1）将浮环端面等效为柔性粗糙表面，壳体平面等效为刚性光滑表面；（2）浮环端面微凸体与壳体平面的接触为半球体与刚性平面的接触；（3）接触表面各向同性；（4）忽略各微凸体间的作用力，且微凸体基底不会发生任何变形，接触示意图如图3所示。

图3 浮环密封端面接触示意图Fig.3 Schematic diagram of floating ring seal end face contact

2.2 浮环密封端面分形接触模型的建立

2.2.1 浮环密封端面微凸体的分形表征 基于第2.1节假设，首先从微观角度建立浮环密封端面单微凸体与刚性平面接触模型，其接触示意图如图4 所示。图中R为微凸体变形前最大的曲率半径，ω为变形前微凸体的高度，l为微凸体的基底长度，l′为微凸体变形后最大的接触直径，δ为微凸体受刚性平面挤压后的变形量。

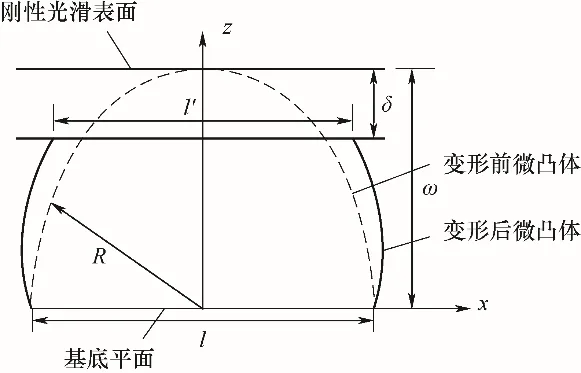
图4 单个微凸体与刚性平面接触示意图Fig.4 Schematic diagram of contact between asperity and smooth rigid surface

根据式(1)，未变形前单个微凸体的外形可表示为

2.2.2 浮环密封端面微凸体的变形机制 根据第

2.2.1 节建立的单微凸体接触模型，计算浮环密封端面微凸体在各个变形阶段的真实接触力及接触面积。由文献[20]可知，接触面微凸体会经历弹性变形、弹塑性变形及塑性变形。

当a ＜ aec时，微凸体处于弹性变形阶段，结合式(3)及式(4)，微凸体在该阶段的接触面积aec及接触力Pec分别为

式中，σy为石墨浮环的屈服应力；E为材料弹性模量。

当aec＜a＜apc时，微凸体处于弹塑性变形阶段，KE 模型[21]将微凸体弹塑性变形阶段分为第一弹塑性变形阶段和第二弹塑性变形阶段，其接触力及接触面积分别为

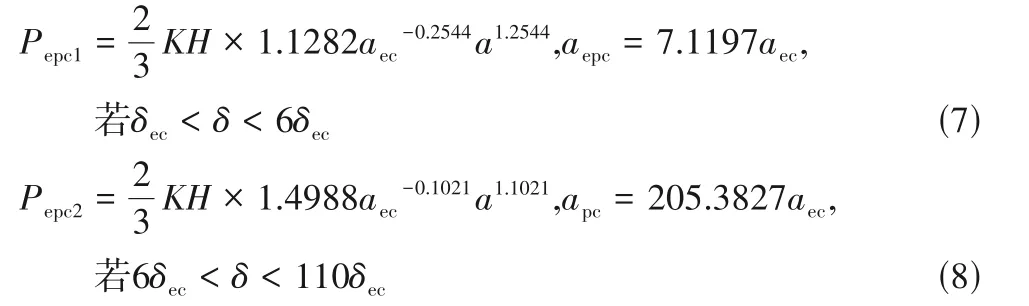
式中，K=0.454+0.4ν，ν为泊松比；H为石墨浮环的硬度；Pepc1及Pepc2分别为微凸体发生第一阶段弹塑性变形和第二阶段弹塑性变形对应的临界接触力；aepc和apc分别为微凸体发生第一阶段弹塑性变形和第二阶段弹塑性变形对应的临界接触面积。

当a＞apc，微凸体进入完全塑性变形阶段，该阶段实际接触面积a及接触力Ppc分别为

2.2.3 浮环密封端面微凸体多尺度分析 由W-M

函数可知，当微凸体频率指数n=nmin时，微凸体基底长度取得最大值lmax= 1/γnmin，当n=nmax时，微凸体基底长度取得最小值lmin= 1/γnmax，所以不同的频率指数n对应不同的微凸体基底长度。根据第2.2.2节分析，不同基底长度的微凸体与刚性平面接触时产生的真实接触力及接触面积也不相同。为了讨论密封端面微凸体多尺度性对于磨损率的影响，采用频率指数n将处于不同变形阶段的微凸体区分开。由文献[20]可知，当微凸体达到弹性变形临界点时，对应的频率指数为

当微凸体达到弹塑性变形临界点时，对应的频率指数为

当微凸体达到塑性变形临界点时，对应的频率指数为

综上可知，频率指数n与微凸体变形特性有关。当接触面频率指数nmin＜n＜nec时，接触载荷作用下微凸体发生弹性变形；当频率指数nec＜n＜npc时，接触载荷作用下微凸体会发生弹塑性变形；当频率指数npc＜n＜nmax时，微凸体发生塑性变形。

2.2.4 密封面实际接触面积和接触载荷 为了计算浮环密封端面总的真实接触面积Ar和接触载荷F，在求得单微凸体各个变形阶段的真实接触力及接触面积的基础上，引用由Wang 等[22-23]提出的改进后的面积分布函数n(a)，结合积分思想，可求得浮环密封端面三个变形阶段真实的接触面积Ar及接触力F。由第2.2.3节可知，当nmin＜n＜nec时，微凸体处于弹性变形，该阶段浮环密封端面的接触面积Aec及接触力Fec分别为

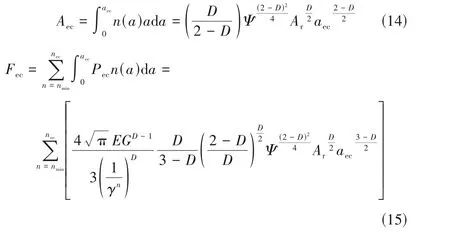
式中，a为微凸体实际接触面积；Ψ为区域扩展系数。

当nec＜n＜nepc时，微凸体处于第一阶段弹塑性变形，可得浮环密封端面第一弹塑性阶段接触面积Aepc1及接触力Fepc1分别为

当npc＜n＜nmax时，微凸体处于完全塑性变形，可得浮环密封端面塑性阶段接触面积Apc及接触力Fpc分别为

2.3 浮环密封端面磨损深度率分形模型的建立

摩擦副在对磨时主要磨损机理是黏着磨损和磨粒磨损[24]，大量的研究表明[25-26]，这两种磨损机理产生的磨损量与法向力和滑移距离成正比，与较软材料的屈服应力成反比，表达式为

式中，M为接触面磨损量；Ke为较软材料的磨损系数；S为滑移距离；σy为较软材料屈服应力。

因为石墨浮环在工作过程中会与壳体形成摩擦副产生持续的滑动摩擦，所以利用式(24)可以计算石墨浮环端面磨损量。对于滑动摩擦，由于同时存在法向正应力和切向剪应力，法向载荷和切向载荷共同作用产生真实接触面积，依据修正黏着理论[27]，屈服应力σy与法向应力σ和切向应力τ之间的关系为

Archard[28]研究发现，磨损系数与接触表面形貌有关，因此本研究中将磨损系数Ke分解为弹性接触磨损系数Ke1，弹塑性接触磨损系数Ke2及塑性接触磨损系数Ke3。将式(14)、式(16)、式(18)及式(20)求得的各个阶段真实接触面积代入式(26)中，并且两边同除以密封端面名义接触面积Aa及时间t，可得浮环密封端面平均磨损深度率计算公式。

式中，h*为平均磨损深度率。

结合式（22）及式（27），可得浮环密封端面平均磨损深度率分形模型为

3 分形模型的验证

为了验证模型的正确性及合理性，本文选用文献[29]中30 钢销和45 钢盘的对磨实验数据进行模型验证，该实验选用的材料参数及工况参数如表1所示。

将表1相关参数代入本文磨损分形预估模型中进行数值计算，求得本文模型在考虑弹塑性阶段及不考虑弹塑性阶段的磨损深度率值，并将理论计算值与文献[29]的磨损实验值进行对比，结果如图5 所示。从图中可以看出考虑弹塑性阶段的模型计算结果与实验数据在总体变化趋势及数值上基本一致，均随着分形维数D的增大，磨损率逐渐减小。文献实验值与本文模型理论计算结果之间最大差值为2.070 × 10-3m/s，最小差值为0.229 × 10-3m/s，在可接受误差范围之内。而不考虑弹塑性变形阶段的模型计算结果与实验数据总体变化趋势差别较大，并且其计算结果与文献实验数据最大差值达到6.070 × 10-3m/s，是考虑弹塑性阶段模型计算结果的3倍，误差很大，不能真实地反映磨损过程。综上所述，考虑弹塑性阶段的磨损分形模型更能反映材料实际磨损规律，并且更加接近于实际的磨损率，具有较好的可用性及预测性。

图5 文献实验数据及本文模型对比Fig.5 Comparison between experimental data in literature and this model

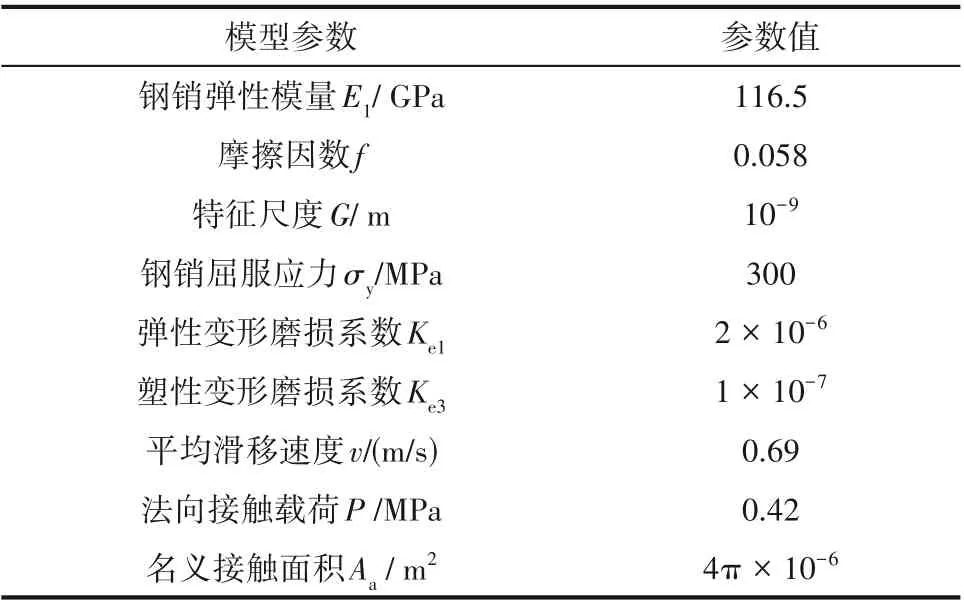
表1 文献实验参数［29］Table 1 Literature test parameter［29］

4 理论计算结果及分析

选用航空发动机密封系统中常用的GH4169 合金钢-石墨组件进行数值分析研究，将石墨浮环密封端面的工况参数、形貌参数及材料参数代入本文磨损率分形预估模型式（28）中进行数值分析，具体参数如表2所示。

4.1 密封端面轮廓分形参数对磨损率的影响

为了分析石墨浮环密封端面的形貌参数对其磨损率的影响。选取不同的分形维数D及特征尺度G计算对应的磨损率，计算结果如图6 所示。随着分形维数D增加，石墨浮环磨损率先减小后增大，造成这一现象的原因是：石墨浮环端面与壳体刚开始相对滑动时，浮环端面比较粗糙，分形维数D较小，单位面积上的微凸体较少，因此单位面积上的法向载荷较大，很容易造成磨屑在反复滑移过程中从微凸体脱落，造成接触表面磨损率较高。随着对磨次数增多，浮环端面逐渐光滑，即分形维数D增大，单位面积上的微凸体增多，表面的支撑能力增强，单位面积法向载荷减小，从微凸体磨损脱落的磨屑减小，从而使磨损率逐渐降低。当浮环端面轮廓分形维数达到某一值Dn时，由于表面过于光滑，接触面间的分子作用力增强，黏着趋势逐渐增大，造成磨损率增大。

从图6 中还可看出随着特征尺度G的增加，石墨浮环磨损率h增大，其原因是特征尺度G表征轮廓曲线上微凸体纵向高度的大小，值越大说明表面越粗糙，密封面相对滑移时造成材料发生大的塑性变形，导致磨损率增大。并且发现当D＜Dn时，特征尺度G对于材料磨损率影响很显著，当D ＞ Dn时，特征尺度G对于材料磨损率影响不明显。其主要原因是：D较小时表面较粗糙，G增大造成材料发生大的塑性变形，所以G对于磨损率的影响很明显；当D ＞ Dn时，密封面被磨得很光滑，这时分子之间的作用力占主导地位，所以G对于磨损率的影响不明显。

从图6(a)、(b)可看出不同的特征尺度G对应不同的D。为了求得最优分形维数D，可对式(28)求导并令其为0，求得一个最优分形维数Dn，使得浮环密封端面磨损率最小。根据石墨摩擦特性，取最大特征 尺 度 为G= 1 × 10-9m，最 小 特 征 尺 度G= 1 ×10-10m，计算结果如图7 所示，最优分形维数Dn随着特征尺度G的增大而增大，并且石墨材料最优分形维数范围为1.45 ≤Dn≤1.65，该结果可用于指导石墨浮环的加工设计及后期维护。

图6 D-G-h关系Fig.6 Relationship of D-h-G

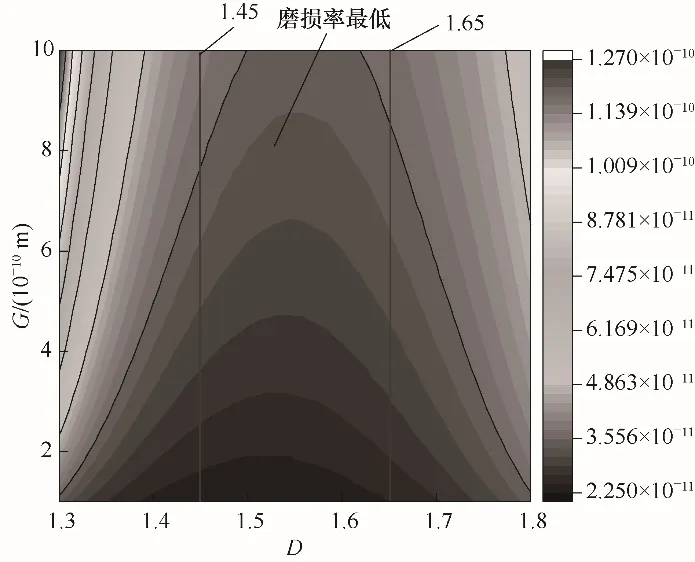
图7 最优分形维数Fig.7 The diagram of optimal fractal dimension

4.2 摩擦因数对磨损率的影响

研究资料表明，石墨材料与金属对磨时摩擦因数变化范围是0.01～0.3，为了分析摩擦因数对于浮环密封端面磨损率的影响，假定摩擦因数会因滑移次数、表面形貌、滑移辐值等原因在0.01～0.3之间变化。理论计算时选用分形维数D=1.5，图8所示为浮环端面磨损率随摩擦因数f的变化规律，磨损率h随着摩擦因数f的增大而按照指数方式增大。其原因是依据能量耗散磨损理论，摩擦因数f越大，滑动过程中产生的摩擦力越大，造成摩擦力做的功越多，这部分功一部分随着热量散失，另一部分储存到密封面微凸体上，当储存于微凸体上的能量达到一个临界值时，磨粒就会从微凸体脱落，所以摩擦因数增大会造成密封面磨损加剧，磨损率增加。该结论可以指导石墨浮环的制造，在保证其正常工作前提下，加工制造时尽可能保证浮环端面具有小的摩擦因数。

图8 摩擦因数-磨损率关系Fig.8 Relationship of friction coefficient and wear rate

4.3 频率指数对磨损率的影响

研究频率指数n对于浮环密封端面磨损率h的影响规律时，取特征尺度G= 1 × 10-9m，密封端面摩擦因数f= 0.07[4,7]。由式(11)、式(12)和式(13)分别求出不同的分形维数D对应的微凸体弹性变形临界频率指数值nec、弹塑性变形临界频率指数值nepc和完全塑性变形临界频率指数值npc，计算结果如表3所示。由石墨浮环粗糙断面采样长度l求得微凸体最小频率指数nmin为9。

表3 微凸体临界频率指数Table 3 The critical frequency index of asperities

由文献[20]可知对于不同大小的微凸体（即频率指数不同），nmin～nmin+5 频率指数水平的粗糙表面微凸体对实际接触面积和接触载荷的贡献是最大的。本文通过选取不同的分形维数D，计算不同频率指数水平的微凸体对密封端面磨损率的影响规律，计算结果如图9所示。从图中可以看出随着频率指数n的增大，不同频率指数水平的微凸体对磨损率的影响越来越小，当n达到16 时，频率指数的大小对磨损率的影响可以忽略不计。其主要原因是随着频率指数n的增大，微凸体基底长度l越来越小（即微凸体越来越小），当频率指数超过一定值时，由于微凸体过小，其对磨损率的影响可忽略不计。并且从图中可以看出分形维数D越大，频率指数n对于磨损率的影响越小，其主要原因是当分形维数D超过1.7 时，浮环端面表面特别光滑，分子间黏着作用占主导地位，频率指数n对于磨损率几乎没有影响，可忽略不计。

图9 频率指数-磨损率关系Fig.9 Relationship of frequency index and wear rate

4.4 滑移速度对磨损率的影响

在研究滑移速度v对石墨浮环磨损率h的影响时，取分形维数D=1.5。如图10所示，在同一特征尺度G下，随着滑移速度v的升高，石墨浮环端面磨损率h会升高。其原因是：随着滑移速度的增大，相同时间内微凸体与刚性平面磨损次数增多，导致浮环端面磨损率增大。

图10 滑移速度-磨损率关系Fig.10 Relationship of slip velocity and wear rate

5 结 论

（1）基于石墨浮环密封端面分形接触模型，考虑微凸体多尺度性、弹塑性变形阶段及密封端面变摩擦因数三个因素，采用Archard 磨损理论及修正黏着理论推导出石墨浮环密封端面分形磨损预估模型，揭示浮环密封端面形貌参数及工况参数对于密封端面磨损率的影响规律。并且通过文献实验数据验证提出的浮环密封端面分形磨损预估模型的可行性。

（2）分形维数对石墨浮环密封端面磨损率的影响具有一定的规律性，随着分形维数D增大，磨损率h先减小后增大，并且存在最优分形维数值，当D=1.45～1.65 时，浮环密封端面磨损率最小，该结论可为石墨浮环生产制造提供一定的理论依据。

（3）当分形维数D一定时，石墨浮环密封端面磨损率h随特征尺度G、表面摩擦因数f及滑移速度v的增大而增大。该结论可以指导浮环的生产设计，在保证其正常工作的前提下，加工时尽可能使浮环端面具有小的摩擦因数及特征尺度，同时尽量减小浮环浮动频率。

（4）石墨浮环端面磨损率仅与最小等级及后续7 个等级的微凸体相关。当密封面的分形维数D＞1.7 时，频率指数n对于浮环端面磨损率的影响可以忽略不计。

为进一步符合航空发动机的浮环密封运行工况，下一步还需考虑温度对于密封端面磨损率的影响，从而建立更精确的浮环端面分形磨损预测模型。

符 号 说 明

Aa——密封端面名义接触面积，m2

Aec——弹性变形阶段浮环密封端面的接触面积，m2

Aepc1——第一弹塑性变形阶段浮环密封端面的接触面积，m2

Aepc2——第二弹塑性变形阶段浮环密封端面的接触面积，m2

Apc——塑性阶段浮环密封端面接触面积，m2

Ar——浮环密封面总的真实接触面积，m2

a——塑性变形阶段微凸体实际接触面积，m2

aec——弹性阶段微凸体接触面积，m2

aepc——微凸体发生第一阶段弹塑性变形对应的临界接触面积，m2

al——微凸体最大接触面积，m2

apc——微凸体发生第二阶段弹塑性变形对应的临界接触面积，m2

D——轮廓曲线分形维数

d1——石墨浮环密封端面内径，m

d2——石墨浮环密封端面外径，m

E——材料弹性模量，GPa

E1——钢销弹性模量，GPa

E2——合金钢弹性模量，GPa

E3——石墨弹性模量，GPa

F——浮环密封端面总接触载荷，N

Fec——弹性变形阶段浮环密封端面的接触力，N

Fepc1——第一弹塑性变形阶段浮环密封端面的接触力，N

Fepc2——第二弹塑性变形阶段浮环密封端面的接触力，N

Fpc——塑性阶段浮环密封端面的接触力，N

f——摩擦因数

G——轮廓曲线的特征尺度，m

H——石墨浮环的硬度，kgf/m2

h*——平均磨损深度率，m/s

Ke——材料磨损系数

Ke1——弹性阶段材料磨损系数

Ke2——弹塑性阶段材料磨损系数

Ke3——塑性阶段材料磨损系数

l——样本的基底长度，m

l′——微凸体变形后最大接触直径，m

lmax——微凸体最大基底长度，m

lmin——微凸体最小基底长度，m

M——接触面磨损量，kg

n——微凸体频率指数

nec——微凸体达到弹性变形临界点时对应的频率指数

nepc——微凸体达到弹塑性变形临界点时对应的频率指数

nmax——微凸体最高频率指数

nmin——微凸体最低频率指数

npc——微凸体达到塑性变形临界点时对应的频率指数

P——法向接触力，N

Pec——弹性阶段接触力，N

Pepc1——微凸体发生第一阶段弹塑性变形对应的临界接触力，N

Pepc2——微凸体发生第二阶段弹塑性变形对应的临界接触力，N

Ppc——塑性变形阶段微凸体接触力，N

R——微凸体变形前最大的曲率半径，m

S——滑移距离，m

v——平均滑移速度，m/s

Z——轮廓曲线高度，m

γ——剖面最低截止频率

γn——随机轮廓的空间频率

δ——微凸体受刚性平面挤压后的变形量，m

ν——材料泊松比

ν1——合金钢泊松比

ν2——石墨泊松比

σy——材料屈服应力，MPa

τb——较软材料的剪切屈服强度，MPa

Ψ——区域扩展系数

ω——变形前微凸体的高度，m

下角标

ec——弹性阶段

epc1——第一弹塑性阶段

epc2——第二弹塑性阶段

pc——塑性阶段