航空发动机振动标准研究
2022-02-18葛向东安中彦
路 阳,葛向东,高 强,武 鹏,安中彦
(中国航发沈阳发动机研究所,沈阳 110015)
1 引言
吊装于飞机或者安装在台架上的航空发动机,是一个具有无限多个自由度的复杂振动系统[1-4],发动机的整机振动是这一系统在各种不同激励同时作用下所产生的复杂振动响应[5-7]。为了推进故障诊断技术的发展,深入研究航空发动机整机振动特征及其变化规律,已成为重要和迫切的课题[8-9]。
当前,航空发动机振动标准采用的是固定标准,即采用单一数值作为发动机全转速范围内的振动限制值[10-12]。但在实际试车过程中,发动机处于不同工作状态下,不同主机测点处的振动水平差异较大[13-14]。因此,单一标准很难保证航空发动机的试车安全,同时对发动机是否存在问题的判断也不够准确。
本文统计了某型航空发动机台架试车过程中主机测点的振动数据,分析了其满足的统计学规律。通过绘制不同转速下振动平均值和瞬时值包络图方法,对该航空发动机的振动特性进行了研究,给出了振动基线[15]。
2 分析方法
研究主要分析了航空发动机台架试车振动数据的正态分布规律。通过绘制参数的概率图和拟合优度检验,来判断数据是否符合正态分布规律,用AD 值和P 值两个指标反映检验效果的好坏。如果样本数据满足分布特征,则采用传统的统计方法,以概率论为基础对数据进行评价,进而根据样本数据对总体进行估计,得出其分布特征参数。样本数据不符合分布特征时,则采用与分布类型无关的方法对参数进行检验,即非参数检验进行数据分析。利用中位数、极值的四分位数、最小值和最大值来描述,并用平均值和中位数的95%置信区间来描述样本特点,得到整个数据列的主要信息。
3 分布规律验证
随机选取该型发动机台架试车过程中,16 次试车数据进行统计学分析。通过绘制参数的概率图,对其进行分布规律拟合优度检验,以判断其是否满足正态分布规律。图1~图5分别为发动机处于慢车、80%、90%、中间和全加力状态时,各测点振动数据在正态分布下95%置信区间的概率图。图中,X轴为选取各个测点的样本数据,Y 轴为数据的累计概率;测点1、测点3 跟踪低压转子,数据单位为mm;测点2、测点4 跟踪高压转子,数据单位为mm/s。概率图与Y 轴为线性的经验累积分布函数图并不相同,通过变换Y 轴,使拟合分布线(中心的蓝线)形成直线。同时显示拟合分布的大约95%的置信区间(左右侧弯曲的蓝线)。拟合分布线表示具有所指参数的所选理论分布的累计分布函数。对于正态分布,使用最小二乘法来估计参数。

图1 慢车状态下各测点振动数据的正态分布概率图Fig.1 Normal probability plot of vibration data under idling rating

图2 80%状态下各测点振动数据的正态分布概率图Fig.2 Normal probability plot of vibration data under 80% status
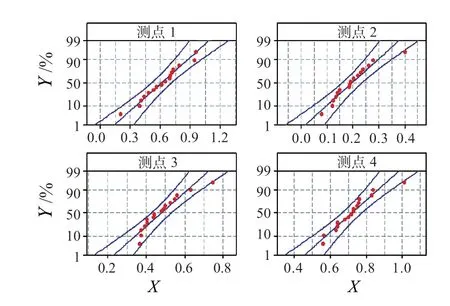
图3 90%状态下各测点振动数据的正态分布概率图Fig.3 Normal probability plot of vibration data under 90% status
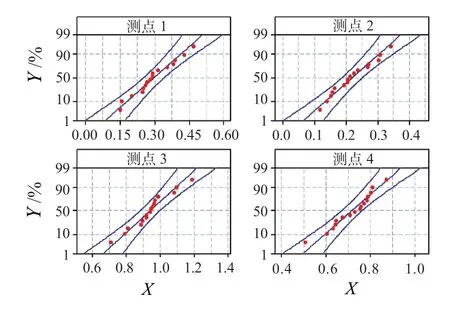
图4 中间状态下各测点振动数据的正态分布概率图Fig.4 Normal probability plot of vibration data under intermediate state
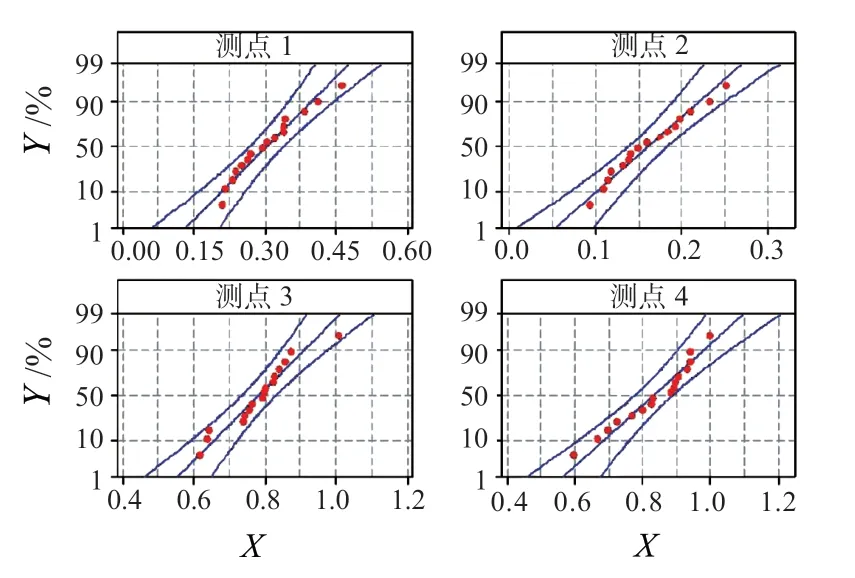
图5 全加力状态下各测点振动数据的正态分布概率图Fig.5 Normal probability plot of vibration data under full augmentation
根据正态分布的概率图进行拟合优度检验,以Anderson-Darling 统计量较小且关联的P 值较大作为拟合度较好的标准。本文取α 水平为0.10,即当P ≥0.10 时,认为测点的振动数据满足正态分布规律。发动机不同状态下试车振动数据的P值如表1 所示。
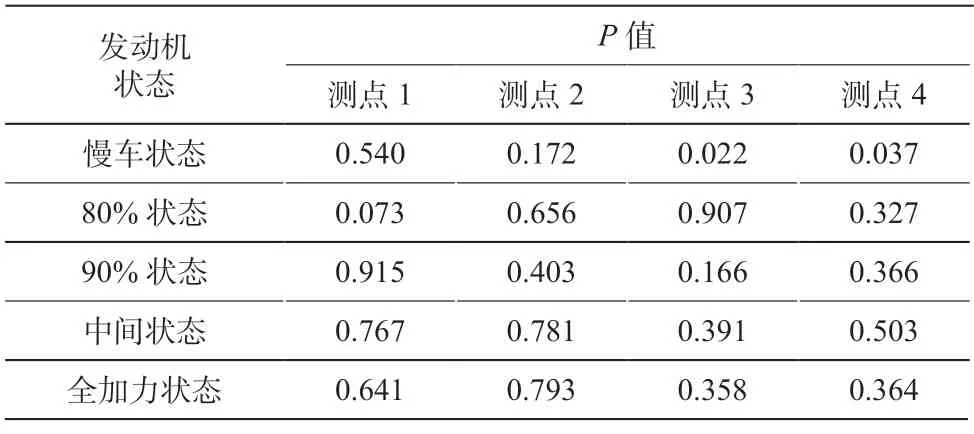
表1 不同发动机状态下各测点振动数据 P 值Table 1 P -value of vibration data of measurement points under different aero-engine conditions
由上述测点振动数据正态分布概率图及拟合优度检验结果可知,绝大多数情况下的振动数值通过了拟合优度检验,满足正态分布规律,可以用于总体样本的推断。仅慢车状态测点3、测点4 和80%状态下测点1 振动数据不满足正态分布,只得到非参数检验的分析结果,需进行后续的数据变换或利用特定的分布函数,来对总体样本进行分析与评估。对不满足正态分布规律的测点振动数据样本,非参数检验分析结果见表2。

表2 非参数化分布特征Table 2 Non-parametric distribution features
4 振动基线
通过绘制振动数据均值和瞬时值95%置信区间包络图的方法,给出各个测点的振动基线。
4.1 振动数据均值包络图

为判定发动机试车过程中,不同状态下振动数据的平均值是否合理,计算测点振动数据均值的95%置信区间。计算公式如下:为发动机各测点振动数据的95%置信区间上限或下限(测点1 和测点3(mm)或测点2 和测点4(mm/s));µ 为样本均值(测点1 和测点3(mm)或测点2 和测点4(mm/s));σ 为标准差(测点1和测点3(mm)或测点2 和测点4(mm/s));n 为样式中:本个数。
根据公式(1),绘制试车过程中发动机不同状态时,各个测点振动值均值的95%置信区间包络图,见图6 。

图6 各测点均值的振动包络图Fig.6 Vibration envelope plot of the mean of measurement points
4.2 振动数据瞬时值包络图
为判断具体的发动机状态下,测点的瞬时振动数值是否正常,计算振动数据样本的95%置信区间。计算公式如下:

式中:σ样本为样本的95%置信区间上限或下限。
根据公式(2),绘制试车过程中发动机不同状态时,各个测点振动值瞬时值的95%置信区间的包络图,见图7。

图7 各测点瞬时值的振动包络图Fig.7 Vibration envelope plot of the instantaneous value of measurement points
4.3 实际应用
利用所得到的振动基线,对同一型号的另一台航空发动机,在台架试车过程中的整机振动进行了监控。整个试车过程中,发动机各主机测点的瞬时和平均振动值均未超过振动包络图的限值,保证了发动机的试车安全。
5 结论
统计了某型航空发动机台架试车过程中主机测点的振动数据,通过绘制概率图及拟合优度检验的方法,分析了其是否符合正态分布规律。利用绘制振动数值均值和瞬时值的95%置信区间包络图的方法,给出了振动基线。归纳、总结的该型航空发动机振动特性,为航空发动机振动标准的制定和优化提供了依据。
