基于西原体模型的非定常岩石蠕变模型
2022-02-18王游卢小雨翟国良
王游, 卢小雨, 翟国良
(1.安徽理工大学土木建筑学院, 淮南 232001; 2.安徽理工大学力学与光电物理学院, 淮南 232001)
许多工程问题如巷道的变形、围岩的失稳、地基的不均匀沉降都表现出较强的时效性[1],即与岩石的蠕变性能有关,作为岩石重要的力学特性,岩石的蠕变性能对于地下工程的开挖、支护、沉降变形观测产生重要影响,而建立合适的蠕变模型是研究岩石蠕变力学特性重要手段,因为它可以揭示岩石的应力-应变-时间三者之间的函数关系。
由于传统蠕变模型存在着不能准确反映岩石蠕变的高度非线性的缺陷,许多学者在传统蠕变模型的基础上通过引入非线性函数和构建损伤元件使其可以更好地模拟岩石蠕变曲线。文献[2]通过把传统西原体模型中的黏性元件改为牛顿体-蠕变体元件进而建立了可以充分描述泥岩蠕变特性的改进西原体模型,该模型不仅参数较少且可以提出模型的破坏的判据。文献[3]建立了以应变作为损伤起始条件并考虑岩石的初始损伤效应的损伤黏性元件,建立了加速蠕变模型。文献[4]用具有硬化效应的非线性黏性元件和损伤弹性元件分别替换Maxwell模型中的相对应元件,建立了可以准确模拟盐岩蠕变曲线的模型。文献[5]进行了不同温度下的盐岩蠕变试验研究,建立了关于温度效应的蠕变模型。文献[6]分析了轴压、水压对裂隙砂岩蠕变性能的影响,建立了关于水压的非线性蠕变模型。文献[7]把黏滞系数修正为应力、时间的函数并引入损伤弹性元件,构建一种新的非线性损伤蠕变模型。文献[8]将分数阶函数应用于结构面的剪切蠕变模型研究中并依据Lemaitre应变等价假说建立了非定常化的加速蠕变模型,该模型可以较好地反映结构面岩体的蠕变特性。文献[9]利用元件模型和分数阶模型来分别描述蠕变的线性、非线性变形,并把加载应力和时间引入到弹性模量和黏滞系数中,建立了适用于成都黏土的非定常蠕变模型,该模型是科学合理的。
综上所述,无论采用哪种方法建立非线性蠕变模型,本质上都是揭示岩石蠕变参数的变化规律,但是现有的蠕变模型往往注重于对加速蠕变阶段的非线性特性的研究,而很少对稳定蠕变阶段的非线性特性进行研究,同时蠕变破坏时间作为岩石重要的力学参数,对正确预测岩体破坏时间有着重要的意义,但基于岩石蠕变破坏时间而建立的加速蠕变模型还不多。基于此,现以西原体模型为基础,构建可以表征岩石稳定阶段蠕变参数非线性特性的黏性元件和关于蠕变破坏时间的损伤黏性元件,建立模拟性能良好的加速蠕变模型,并验证该模型的适用性,同时分析模型参数对蠕变曲线的影响,以期为蠕变模型的建立提供参考价值。
1 非线性模型建立
1.1 典型蠕变曲线
根据应力水平不同,岩石蠕变曲线可大致分为两类[10](图1):①当岩石加载应力处于中等水平及以下时,岩石的蠕变曲线为稳定蠕变,此时岩石蠕变曲线有一个较大的初始蠕变变形,岩石的蠕变速率刚开始较大,随后蠕变速率一直衰减直至岩石变形保持稳定,岩石蠕变变形主要为弹性变形、黏弹性变形;②当岩石加载应力水平处于较高水平时,岩石的蠕变曲线为不稳定蠕变,此时岩石蠕变曲线不仅包括稳定蠕变,还包括不稳定蠕变,这时岩石蠕变变形包括弹性变形、黏弹性变形、黏塑性变形,岩石在这一阶段会发生蠕变破坏。为了表征岩石的变形的复杂性,往往采用多种线性元进行串并联组合,但基于线性元件而建立的蠕变模型无法表征岩石加速蠕变的非线性特征。
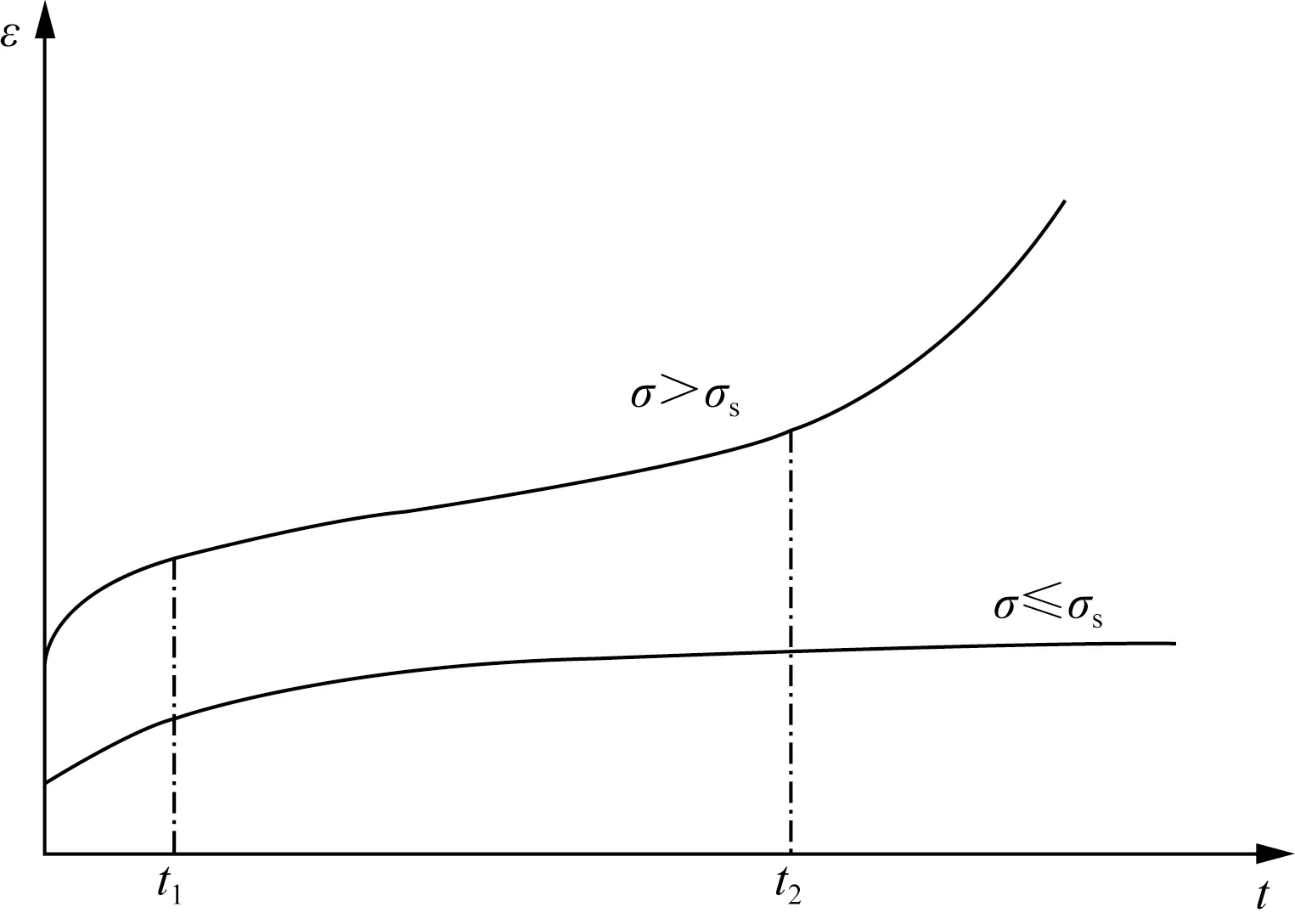
t1、t2分别为等速蠕变、不稳定蠕变启动时间;σ、σs分别为加 载应力、岩石长期强度;ε为蠕变应变;t为加载时间图1 典型蠕变曲线图Fig.1 Typical creep curve
1.2 非线性损伤西原体模型
在蠕变模型中常用Kelvin模型来模拟岩石的稳定蠕变阶段,但有时Kelvin模型对岩石稳定蠕变的模拟效果并不精准,其原因是Kelvin模型的参数是定常的,但岩石作为多种矿物成分和不同孔隙组成的集合体,其力学特性复杂,同时岩石蠕变参数在岩石蠕变过程中不断发生变化,因此为了准确表征岩石蠕变的非线性特征必须对模型元件进行非线性改进。大量研究成果表明岩石在稳定蠕变阶段存在明显的蠕变硬化效应,即黏滞系数随时间不断增加直至达到定值[11]。因此为了更加准确、合理地反映岩石蠕变的力学机理和模拟岩石稳定蠕变曲线,假定在Kelvin模型中黏性元件的黏滞系数符合以下表达式:
(1)
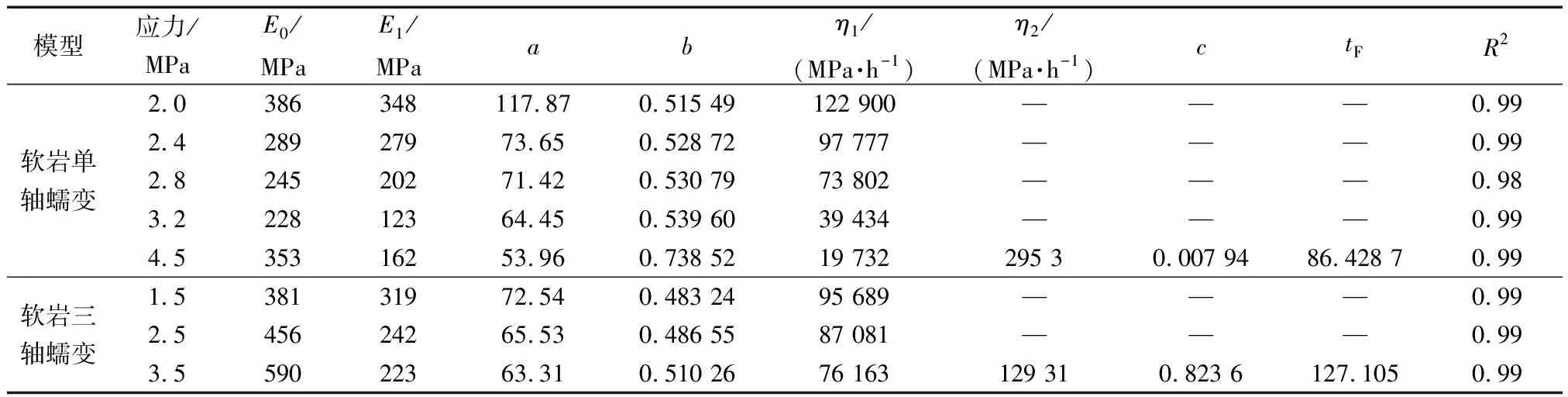
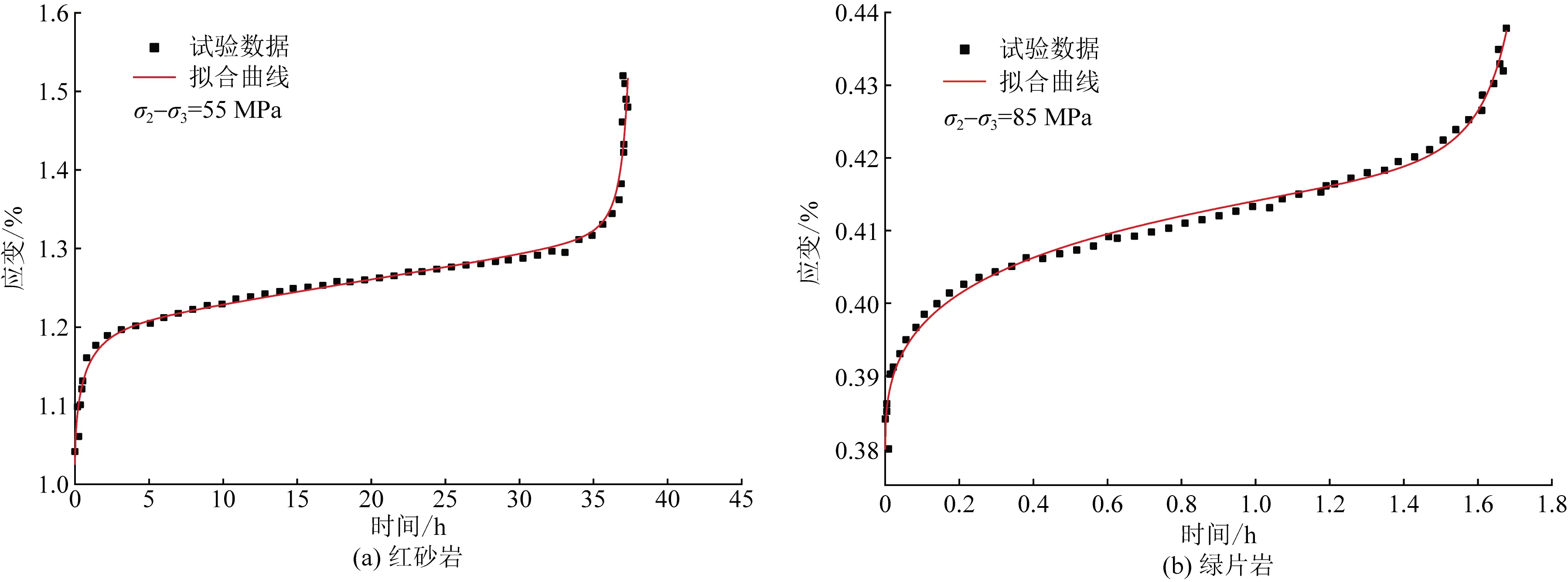
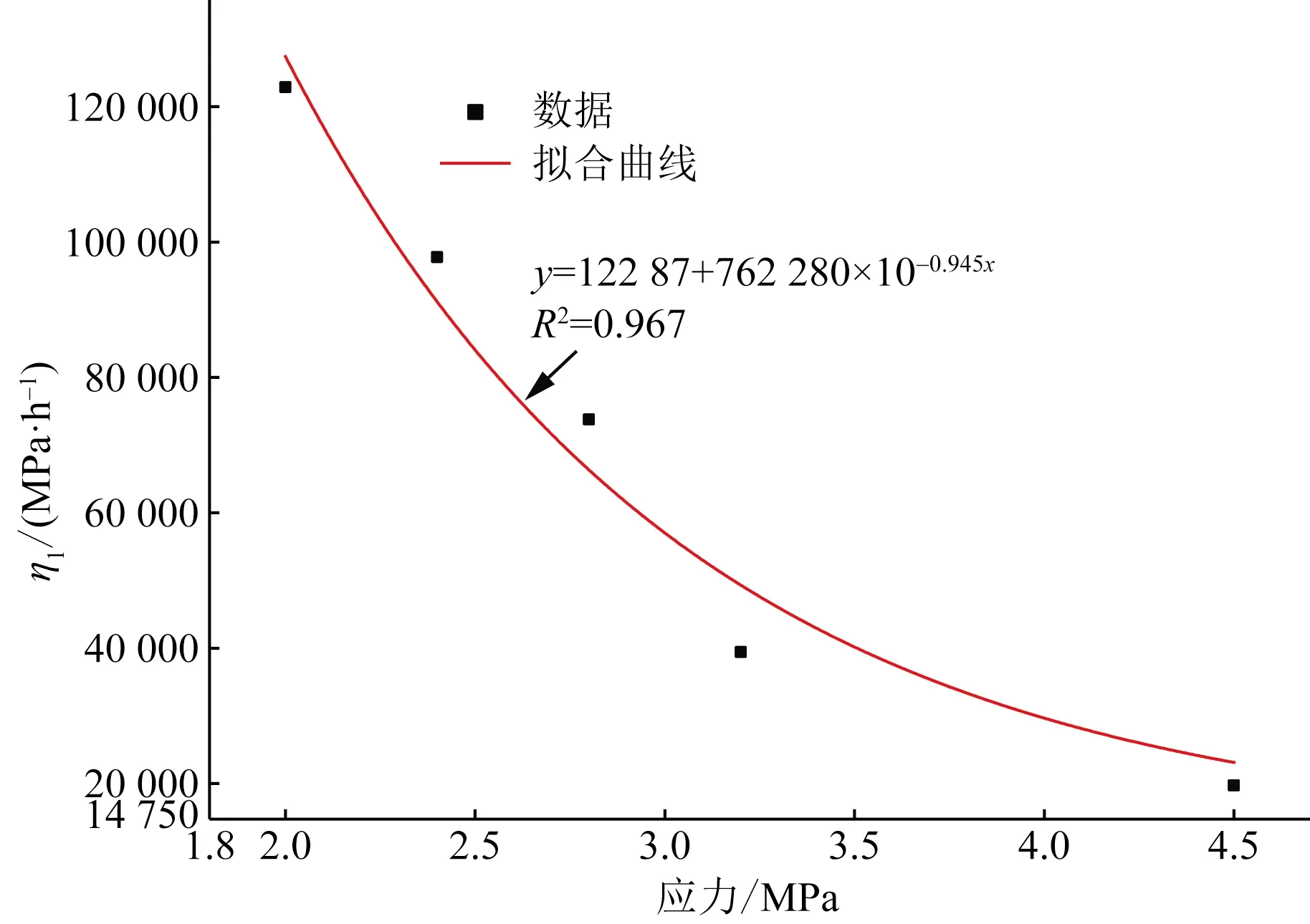
式(1)中:η(t)为表征t时刻Kelvin模型的黏性元件的黏滞系数;η1为Kelvin模型的黏性元件的初始黏滞系数;a、b为蠕变参数;a>0,0 式(1)对时间求导可得 (2) 当岩石加载应力超过岩石的长期强度时,岩石内部裂纹会发生不稳定扩展,导致岩石的力学性质逐渐劣化,岩石产生损伤继而引起蠕变变形迅速增加,导致岩石发生蠕变破坏。现提出一个损伤变量表达式[式(3)],即加载时间、蠕变破坏时间的表达式: (3) 式(3)中:c为损伤参数;tF为蠕变破坏时间;t为蠕变时间。 当t=0时,D=0,对应岩石无损伤或者损伤效应很小可以忽略不计;当t→tF时,D→1,对应着岩石完全破坏。 西原体模型[12]可以描述岩石的衰减蠕变和应力超过长期强度的等速蠕变,但无法模拟岩石的加速蠕变,为了使模型可以反映岩石蠕变的非线性特征和能对岩石加速蠕变曲线进行模拟,将非线性黏性元件引入Kelvin模型中和构建损伤黏性元件进而建立非线性损伤西原体模型,模型如图2所示。 图2 非线性损伤西原体模型Fig.2 Nonlinear damage Nishihara model 相应的状态方程如下。 (1)当σ≤σs时,模型的状态方程为 (4) (2)当σ>σs时,模型的状态方程为 (5) 1.3.1 一维蠕变方程 由式(4)和式(5)的状态方程可得相应的一维本构方程。 (1)当σ≤σs时,模型的一维本构方程为 (6) (2)当σ>σs时,模型的一维本构方程为 (7) 式(6)和式(7)经过Laplace变换和Laplace逆变换后可得相应的一维蠕变方程为 σ≤σs (8) σ>σs (9) 1.3.2 三维蠕变方程 对于一般的岩土工程,岩石的应力状态往往是三向受压的,因此建立三维蠕变方程更加有利于在工程上推广。由弹性力学可知,岩石内部一点的应力σij可分为偏应力张量Sij和球应力张量σm,同理应变εij可分为偏应变张量eij和球应变张量εm[13]。对于绝大多数材料来说,偏应力张量只会引起偏应变张量,球应力张量只会引起球应变张量,并且在岩石蠕变过程中,岩石的蠕变变形只与偏应力张量有关,而与球应力张量无关。由弹性力学可以写出弹性体的三维本构方程为 (10) 式(10)中:E为弹性体弹性模量;K为弹性体的体积模量;G0为弹性体的剪切模量;μ为泊松比。 当岩石进入到加速蠕变阶段时,其变形不仅包括黏弹性变形,还包括黏塑性变形。对于黏弹性变形部分可以类比于一维蠕变方程的推导方法,但黏塑性变形部分的蠕变方程的推导不仅与屈服函数有关,还与流动法则有关[14]。由广义塑性力学可知,对于岩石类材料,其流动法则应采用相关联流动法则,则黏塑性变形的本构方程为 (11) 在常规三轴压缩试验中,一般有σ2=σ3,则 (12) 式(12)中:J2为偏应力第二不变量。 由前面的假设可知,其屈服函数F为 (13) 将式(10)~式(13)代入式(8)和式(9)可得非线性损伤西原体模型的三维蠕变方程: σ>σs (15) 岩石蠕变模型参数包含E0、E1、η1、η2、a、b、c、tF8个参数,其中tF为岩石蠕变破坏时间,可由岩石蠕变曲线直接得到,E0可由岩石蠕变曲线的瞬时弹性变形得到,剩余参数利用Origin软件自带的Levenberg-Marquardt算法求解。引入文献[15]在冻结温度T=-10 ℃所做的软岩单轴和三轴蠕变试验数据来验证该模型的适用性及进行参数辨识,得到的拟合曲线如图3所示,拟合参数如表1所示。 引入文献[14]和文献[16]的加速蠕变数据进一步验证该模型的适用性并对三维蠕变方程系数进行简化,简化得到的方程为式(16)所示,拟合曲线如图4所示,模型参数如表2所示。 ε(t)=a0+a1{1-exp[-a2(t+atb)]}+ (16) 图3 拟合曲线与试验曲线对比Fig.3 Comparison of fitted curve and test curve 表1 软岩蠕变拟合参数Table 1 Soft rock creep fitting parameters 图4 拟合曲线与加速蠕变试验曲线对比Fig.4 Comparison of fitting curve and accelerated creep test curve 表2 加速蠕变拟合参数Table 2 Fitting parameters of accelerated creep 从图3和图4中的拟合曲线与蠕变试验曲线的对比情况来看,建立的非线性损伤西原体模型对不同应力下的岩石蠕变曲线的模拟性能都良好,且模型参数的取值也在合理范围之内。 图5是参数a和参数b不同取值对岩石蠕变曲线的影响;图6是参数η1与应力的关系图;其余参数如表1所示,加载应力为2.8 MPa。 由图5可知:随着参数a、b取值的增大,岩石衰减蠕变曲线越不明显,持续时间也较短,岩石越快的进入稳态蠕变阶段,岩石的稳态蠕变速率也相应减小且随蠕变时间一直衰减,但在相同时刻下岩石的蠕变变形量相应变大。这说明非线性Kelvin模型具有明显的衰减蠕变和稳态蠕变且蠕变速率的变化也可以表征岩石蠕变硬化的非线性特征。 由图6可知,黏滞系数η1随应力呈指数衰减,而黏滞系数η1直接影响岩石的衰减蠕变曲线半径和进入稳态蠕变阶段的时间,图6表明,随着应力的增加,岩石的衰减蠕变曲线越发明显,岩石进入稳态蠕变的时间越晚。 图7为参数c不同取值对岩石蠕变曲线的影响,其余参数如表1所示,加载应力为4.5 MPa。 由图7可知,参数c的取值对岩石稳定蠕变的影响较小,主要影响岩石的加速蠕变曲线形态;随着参数c取值的增大,岩石的蠕变变形和蠕变速率也相应非线性增加,参数c可以表征岩石加速蠕变的非线性特征。 图5 不同参数取值下对蠕变曲线的影响Fig.5 The influence of different parameter values on the creep curve 图6 参数η1与应力关系图Fig.6 Relationship between parameter η1 and stress 图7 参数c对岩石蠕变曲线的影响Fig.7 Influence of parameter c on creep curve (1)在西原体模型的基础上,将非线性黏性元件替换Kelvin中常规黏性元件和构建了关于蠕变破坏时间的损伤黏性元件,得到了非线性损伤西原体模型,并同时推导了该模型的本构方程、一维和三维蠕变方程。 (2)引入前人所做的蠕变试验数据对建立的蠕变模型进行验证。结果表明理论曲线和试验曲线吻合程度较高,非线性蠕变模型可以模拟不同应力下的岩石蠕变曲线。 (3)对模型参数进行分析表明,随着参数a、b的增加,岩石衰减蠕变曲线越不明显,岩石的稳态蠕变速率也相应较小,由于引入非线性函数,Kelvin对岩石稳定蠕变曲线可以更加精准的描述,且能适应岩石蠕变的非线性特征;参数c主要影响岩石的加速蠕变曲线,随着参数c取值的增加,岩石蠕变变形量和蠕变速率也相应增加。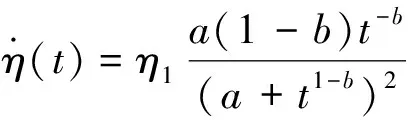
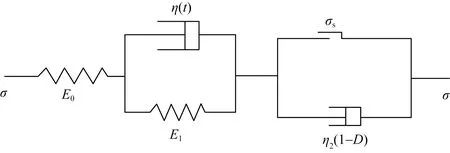
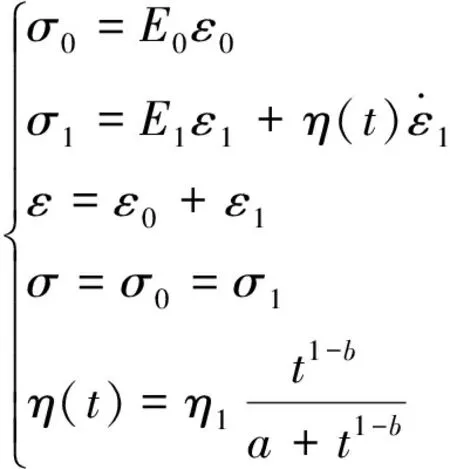
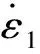
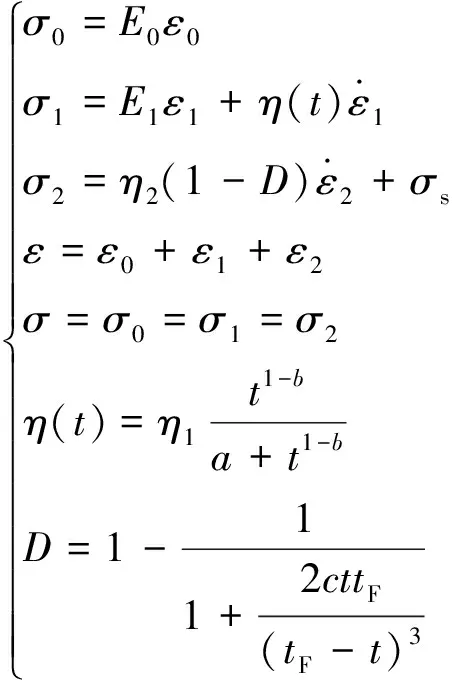
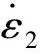
1.3 蠕变方程

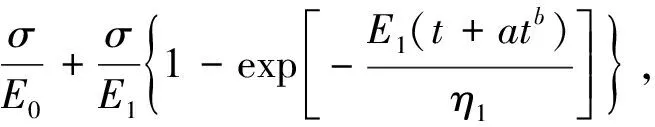
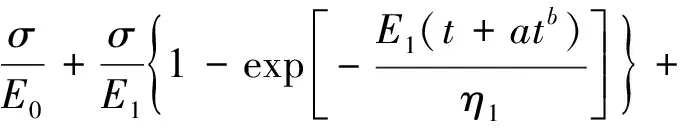


2 模型验证及参数辨识



3 参数分析
3.1 参数a、b、η1分析
3.2 参数c分析


4 结论
