基于螺旋理论对4-URU并联机构自由度分析*

王 远

（1.山西工程职业学院机械电子工程系，山西 太原 030009；2.中北大学机械工程学院，山西 太原 030051）

0 引言

近年来，并联机器人的性能特点逐渐被机器人科研工作者所研究，和串联机器人相比，并联机器人因其突出的稳定性、刚度、承载能力以及精度等结构特性被应用到工业、航天、农业等领域[1]。并联机器人首次进入大众视野是Stewart提出的Stewart并联机器人的形式，该机构的设计是用来对飞行员进行训练的[2]，后来被众多研究者继续开发出各种不同形式的并联机构[3]；Delta机器人是目前在工业生产线上应用较为广泛的并联机器人，具有四个自由度，由三条臂组成，这三条机械臂通过万向关节和基座相连[4]，根据该并联机器人的结构组成及特点，可认为是平行四杆机构的延伸与拓展[5]。由于机器人的研究需要大量的数学理论作为研究基础，随着数学理论和机构学理论的不断融合，使得串联、并联机器人的研究有了一系列不同程度的突破[6]。拓扑图论、旋量理论、李群、李代数、四元数等各种数学工具不断被研究人员引入机构学理论，使机构学理论有了大量的创新与发展[7]。

螺旋理论（也称为旋量理论）的引入对机器人的构型及自由度类型的研究有着举足轻重的作用[8]。螺旋理论在创立之初一直无人问津，直到20世纪中叶，Dimentberg应用螺旋理论对空间机构进行分析时才被研究人员所了解[9]。

目前，针对串联、并联以及混联机器人的研究大多数对机器人的构型、自由度、运动学、动力学以及工作空间等进行分析，这些性能指标的好坏将直接影响机器人的工作精度、工作速度以及工作稳定性[10]。作为这些指标的基础，机器人自由度的研究已经有了较为全面的发展，本研究采用旋量理论对一种4-URU并联机构进行自由度分析，通过传统的G-K自由度公式和旋量理论进行对比，得出旋量理论的应用对自由度的求解具有较好的直观性，具有很大的科学研究价值。

1 自由度计算

4-URU空间并联机构简图如图1所示，该机构由四个相同的URU支链、动平台n1以及静平台n2组成，和静平台n2连接的是虎克铰（U副）。初始状态下，其中的一个R副轴线垂直于静平台。和该运动副相连接的是连杆l1，连杆l1和l2通过R副相连接，R副轴线平行于静平台。连杆l2的另一端通过U副与动平台相连接。

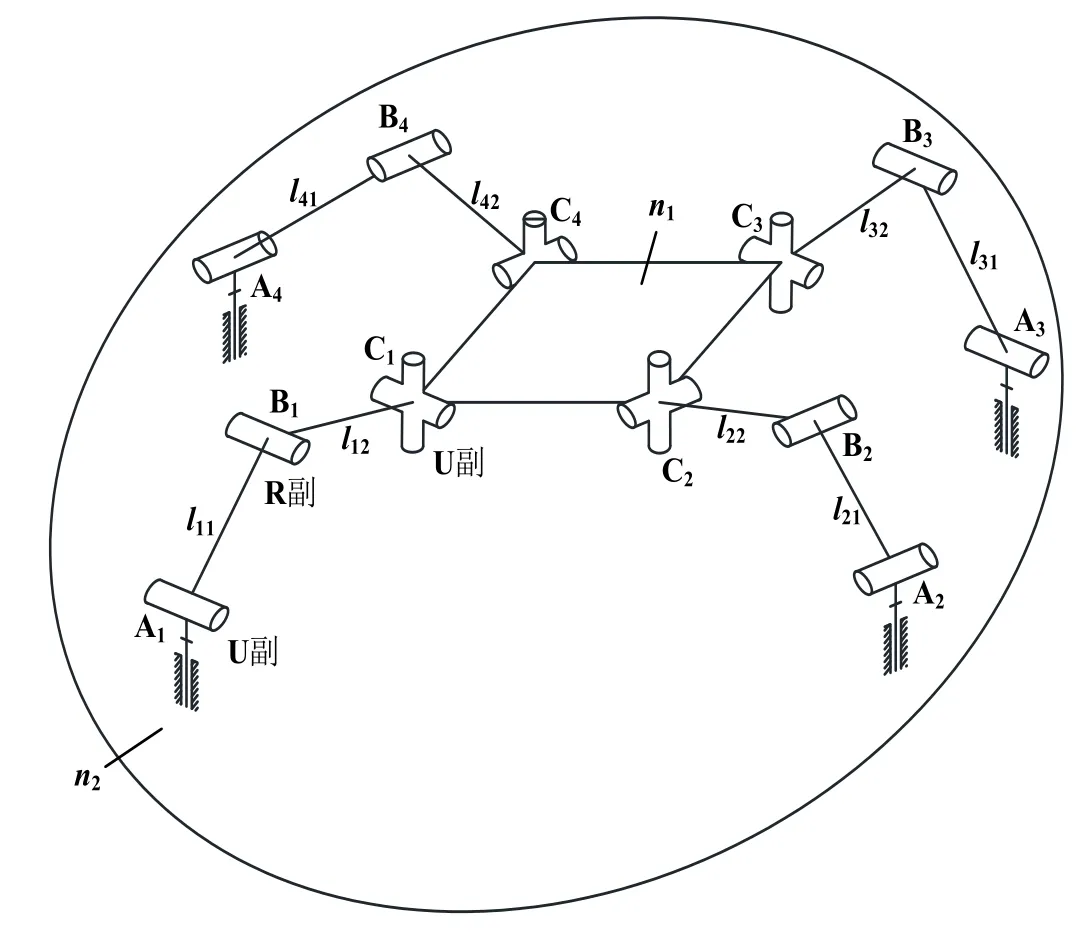
图1 空间4-URU并联机构简图

在该机构的四条支链中，支链A1B1C1和支链A3B3C3相对应的运动副的轴线平行，支链A2B2C2和支链A4B4C4相对应的运动副的轴线平行，支链A1B1C1和支链A2B2C2相对应的运动副的轴线相互垂直。从图1中可以看出，这四条支链的自由度数都是相同的，因此只需要对其中的一条支链进行分析。现以支链A1B1C1作为研究对象开始分析。

支链A1B1C1的旋量分析示意图如图2所示。该支链由两个U副和一个R副组成，U副可看作由两个轴线相互垂直的R副组成。因此，该支链的运动副可认为由5个R副组成，其中有3个R副的轴向是相互平行的。最下面的R副轴向与静平台垂直。

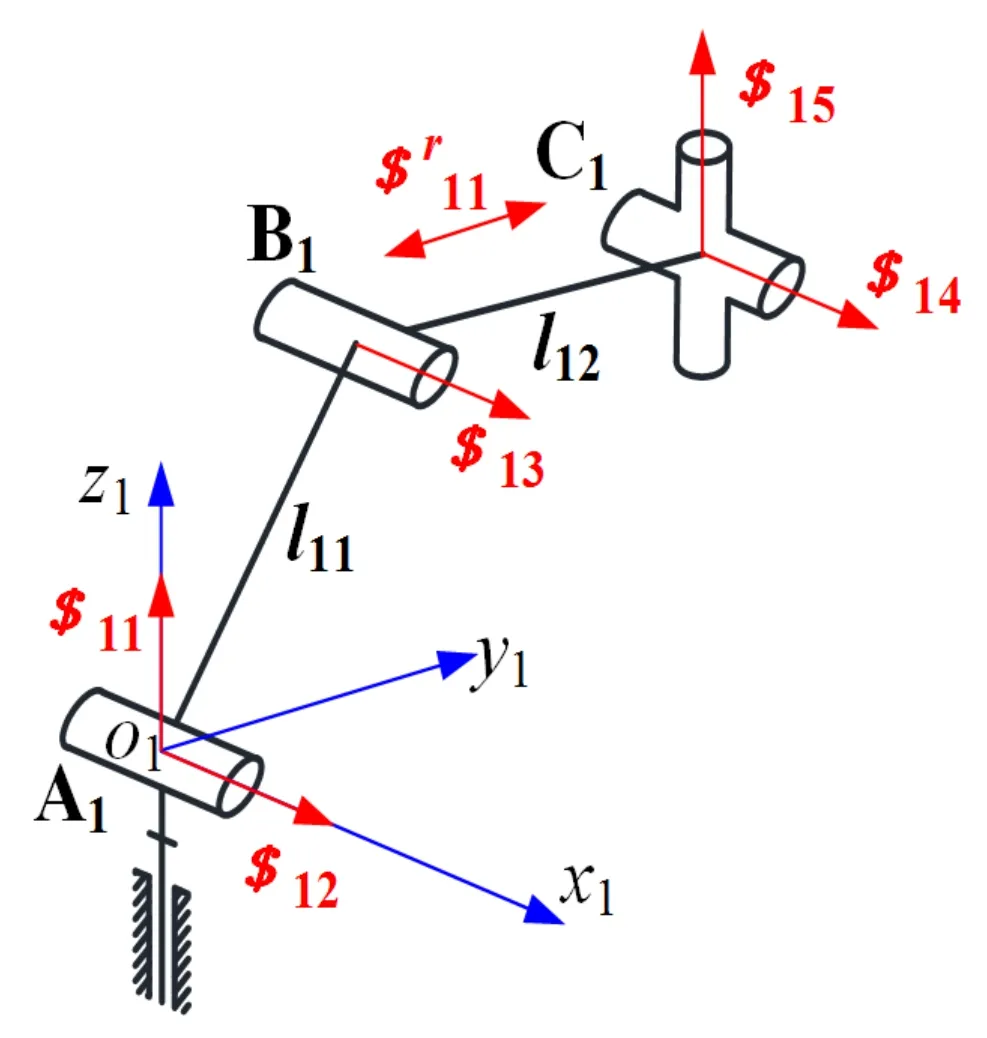
图2 支链A1B1C1的旋量分析图

在支链A1B1C1上建立坐标系o1-x1y1z1，根据旋量理论，一个螺旋如$=（S，S0），S表示的是转动，S0表示移动，由于该支链只有转动副，因此这5个R副可通过5个螺旋来表示。

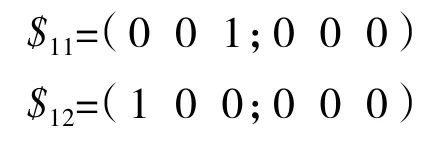
以上这5个螺旋组成支链A1B1C1的运动螺旋系。欲求出该支链的自由度，只需要求出该螺旋系的反螺旋即可。式（1）中e3、f3、e4、f4、d5均为标量，这些标量的取值不影响反螺旋的求解。由于该反螺旋与式（1）中任意一个螺旋的互易积都为零，因此可得到：

根据式（1）和式（2）可求出该反螺旋：

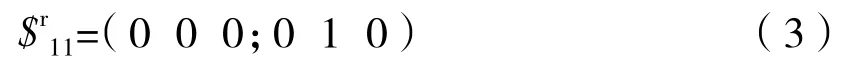
观察该反螺旋可知，该螺旋是个约束力偶，如图2中用双箭头所表示的力偶该力偶平行于y1轴，并且该力偶垂直于U副中两个R副的轴线。因此可知，支链A1B1C1具有一个沿y1轴线方向的约束力偶，即限制了绕着y1轴线的转动。由于该4-URU机构具有四个相同的支链，因此可以建立如下反螺旋系：

可以看出该反螺旋系线性相关，因此该反螺旋系中有两个虚约束。若继续对式（4）进行反螺旋求解，将会得到该机构需要的自由度，如式（5）所示：

从式（5）可以很明显看出，该4-URU并联机构具有4个自由度，分别是3个移动自由度以及1个绕着Z轴的转动自由度[11]。

该自由度结果可通过修正的G-K公式进行验证。式（6）中，d=6，n表示构建的总数，g表示运动副的数目，fi表示第i个运动副的自由度数。由于该机构具有两个过约束，v=2，可得：

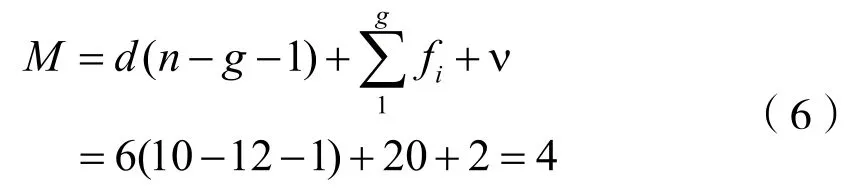
2 结论

尽管通过修正的G-K公式可解出并联机构的自由度数目，却无法求出每个自由度的类型，而通过旋量理论不仅可解出机构的自由度数目，还能判断出每个自由度的类型。因此，利用旋量理论来求解机构的自由度具有非常大的优势。