基于混合内点罚函数法和牛顿法的减速器齿轮传动参数优化分析

2022-02-18曹劲飞

南方农机 2022年4期

曹劲飞

（长安大学工程机械学院，陕西西安 710064）

齿轮机构由于其传动比为常数，所以有传动平稳、冲击振动小、噪声低等特点，故在工程上有着广泛的应用。而针对齿轮传动的结构优化方面，近年来提出的新型算法应用研究较多，对其具体结构的适用性和可靠性的讨论甚少[1]。针对相关研究的不足，笔者对实际齿轮结构应用混合内点罚函数法和牛顿法优化其核心六个参数，讨论算法的可靠性以及优越性，并且将优化之后的参数同之前进行对比，得到优化率。

1 模型介绍

单级减速器齿轮传动的示意图如图1所示[2]：

图1 单级减速器齿轮传动示意图

图中，L1、L2、Lz分别为主动轴伸出长度、从动轴伸出长度和支承长度；d1、d2分别为主动轮和从动轮的节圆直径，d3、d4分别为主动轴和从动轴的直径。考虑实际减速器的结构和常用齿轮形式，因主动轮直径较小，故拟选用实心轮形式；从动轮拟选用腹板式齿轮。主、从动轮如图2所示。

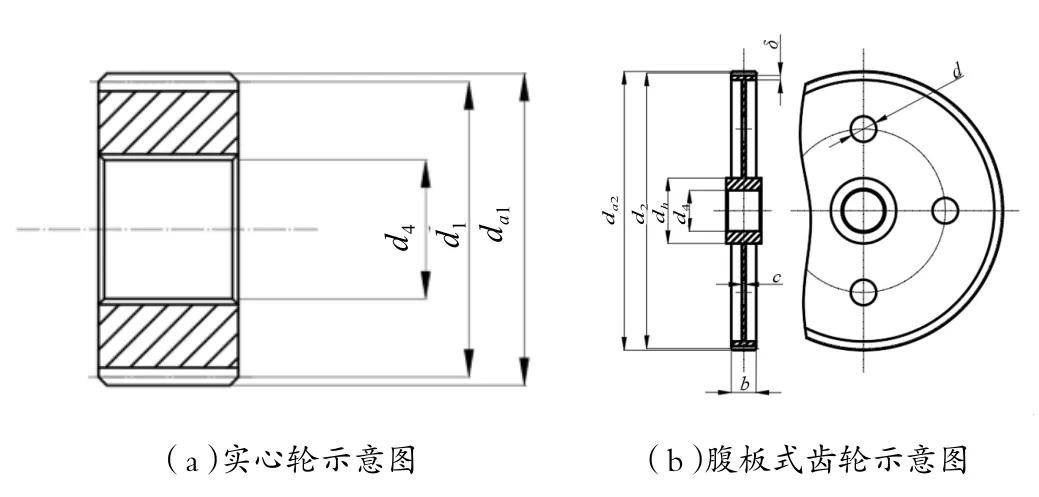
图2 主、从动轮示意图

图中的符号表示参数和计算公式如表1所示定义。

表1 符号定义

2 优化过程分析

2.1 优化设计理论

每个优化问题的具体要求和约束条件各不相同，但抽象出来的数学模型通常都是由设计变量、目标函数和约束条件构成。而优化设计问题通常可以归纳为：选取适当的设计变量，在使所有设计变量满足所需要的约束条件情况下，选取设计变量的最优取值，使得目标函数表达式取到可行域内的最值。整个优化过程利用数学模型表达和解释如下。

选取设计变量：

使设计变量满足所有等式约束和不等式约束条件。而约束条件又分为边界约束和性能约束两种。所谓边界约束是指根据设计要求，设计变量必须满足的几何条件以及只对设计变量的取值范围加以限制的约束。例如将x1变量长度限制在[Lmin,Lmax]范围之内，则有约束条件：

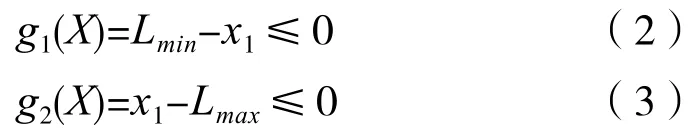
性能约束则是指根据性能要求而建立的限制条件。例如构件的实际工作应力σ与许用应力[σ]之间的约束、梁挠度y与许用挠度[y]之间的要求。据此，约束条件可表述为：

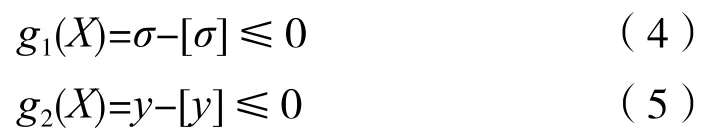
在设计变量满足所有约束条件的前提下，使得目标函数f(X)=f(x1,x2,x3,…,xn)取得极值。因此，最终优化设计数学模型为[3]：

2.2 设计变量的确定

众所周知，在优化设计中，设计变量的个数越多，设计空间的维数越高，设计的自由度也越大，可供选择的设计方案也就越多，但是随之而来的是设计难度的陡增和计算程序的复杂化。因此，在建立优化设计的数学模型时，应尽可能地只把对优化目标影响显著的参数作为设计变量，以减少设计变量数目，而又尽量不影响优化效果。

如表1所示，在单级齿轮传动中，包括主动轮、主动轴、从动轮和从动轴的多个设计参数。需要选取其中的核心设计参数。基于轻量化的目的，首先，确定齿轮的质量需要齿宽、齿数和齿轮模数，所以此处选取主动轮的齿宽、齿数和模数作为三个核心设计参数[4]。根据传动比、正确啮合条件和选取齿轮的形式，便可以计算出从动轮的设计参数和两个齿轮的质量。正确啮合条件如下所示。

1）啮合齿轮的模数必须相等并且等于标准模数[5]。2）啮合齿轮的压力角必须相等并且等于标准压力角。3）主、从动轴设计参数的确定。每根轴的长度都可以分为两个部分，分别是减速器内轴的支撑长度和减速器外轴的附属长度。由于两根轴的附属长度往往由上级传动和下级传动确定，所以不必选为设计参数；又由于主、从动轴的支撑长度相等，所以只需将支撑长度设为一个设计参数即可。支撑部分质量还需要两根轴的直径才能确定，所以又选取主动轴直径和从动轴直径作为设计参数。

综上所述，确定了六个核心参数，减速器的质量可以完全确定。将这六个参数设置为设计变量，有：

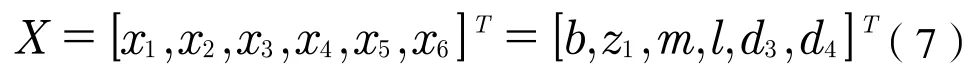
2.3 目标函数的确定

由上述可知，对于减速器来说，在保证约束条件要求的情况下，降低减速器质量成为本次优化设计要求的目标。所以，将减速器总质量最小作为目标函数，如式（8）～（11）所示。

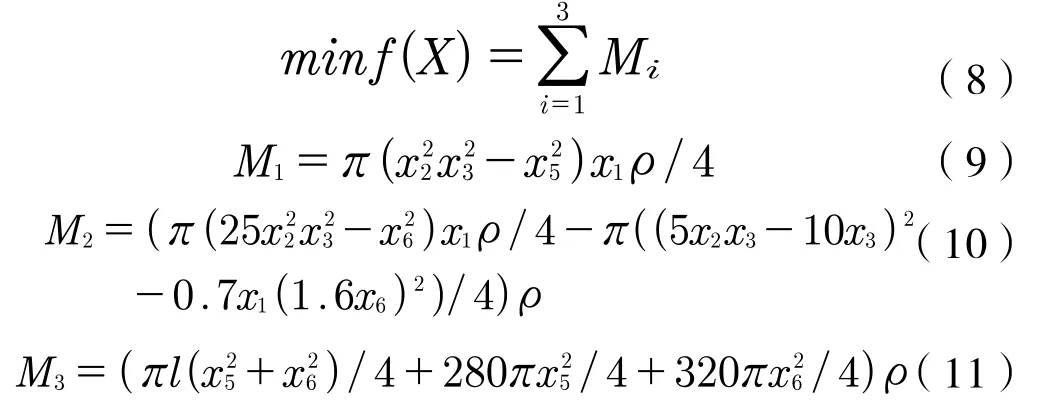
其中，M1、M2分别为主、从动轮质量计算公式，M3为主、从动轴质量计算公式。此处假设主、从动轴和齿轮使用同样的结构钢进行制作，所以材料密度相等，故目标函数可以转化为体积最小化。

2.4 约束条件的建立

2.4.1 齿轮模数约束

减速器中主动轮和从动轮均为传力齿轮，用来传递动力的齿轮模数不宜过小，模数取值一般以超过2 mm的标准模数为优，如式（12）所示：

2.4.2 齿轮齿数约束

在模数和传动比已经确定的情况下，主动轮的齿数越少，从动轮的齿数也越少，齿轮机构的中心距、尺寸和质量也会减小。但是对于渐开线标准齿轮，其最少齿数是有限制的，齿顶线不应该超过啮合线的极限点。若超过顶点，超过部分不仅不能展开成渐开线齿廓，还会将根部已加工出的渐开线切去一小部分，这种现象称为根切。为了避免根切，查阅设计手册[6]，对于压力角取20°和齿顶高系数取1的正常齿制标准渐开线齿轮，其最少齿数为17，故可以转化为如式（13）：

2.4.3 齿轮齿宽系数约束

约束主动轮的齿数和模数之后，确定齿轮结构还需要约束其齿宽系数，如式（14）所示：

式中d为大齿轮直径，此式常用来确定大齿轮齿宽，小齿轮齿宽在大齿轮齿宽的基础上加上5 mm ~10 mm即可。齿宽系数的范围通过查阅文献获得。本研究中齿轮属于非对称布置，并且对于减速器中齿轮一般选用闭式软齿面齿轮传动。故对齿宽系数的约束如式（15）～（16）所示：

由于大齿轮选用腹板式齿轮，小齿轮选择实心式齿轮，故对两者的齿顶圆直径都有相应的约束。查阅设计手册，对于腹板式齿轮结构，其齿顶圆直径一般小于等于500 mm；对于实心式齿轮，其齿顶圆直径一般小于等于160 mm。可以转化为式（17）～（18）：

齿轮的主要边界约束条件基本得到约束，继续列写主动轴和从动轴的边界约束条件。按设计经验，单机圆柱齿轮减速器的主动轴和从动轴的取值范围一般为[100,150]和[130,200]，如式（19）～（22）所示：

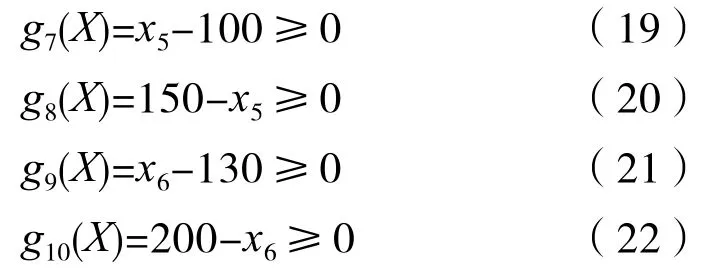
对于传动轴来说，其直径应该小于齿轮的齿根圆直径。所以对于两根轴还有如式（23）～（24）的约束：

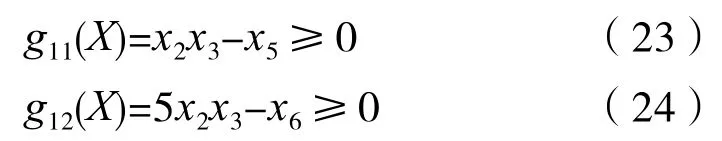
在齿轮的设计计算方法中，针对本研究中选择的闭式软齿面齿轮传动，齿面接触强度较弱，先按齿面接触强度进行设计计算，然后校核齿根弯曲疲劳强度[7]。故在此需要对两个齿轮的齿面接触强度和齿根弯曲疲劳强度进行约束。小齿轮的材料选用40MnB调质，大齿轮采用ZG35SiMn调质。则小齿轮的齿面接触强度和齿根弯曲疲劳强度分别为720 MPa和595 MPa；大齿轮的分别为615 MPa和510 MPa，最小安全系数SH和SF分别取1.1和1.25[8]。许用应力如式（25）～（28）：

齿轮的齿面接触强度和齿根弯曲疲劳强度计算公式如式（29）～（30）：

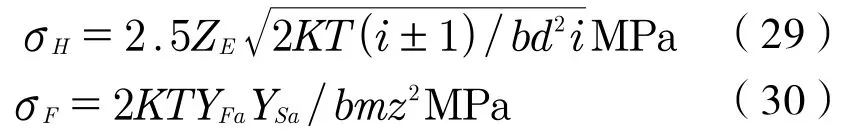
式中K称为载荷系数，由于减速器的原动机为电动机而且工作室载荷特性较为均匀，故K取1；系数ZE称为弹性系数，根据本文中齿轮所选材料参数，取189.8；T为主动轴上输入扭矩，取2.674×106N·mm；YFa、YSa分别为外齿轮的齿形系数和外齿轮的应力修正系数，其取值应该根据齿数而定，在此根据减速器未经优化的数据进行取值。对于小齿轮分别为2.9和1.5；对于大齿轮分别为2.2和1.8。确定了公式和其中参数的取值之后便可以依据式（31）写出约束[9]：

寻找传动轴的性能约束。强度约束条件表述的是在承受载荷时轴的结构不至于失效；刚度约束条件表述的是在承受载荷时轴的实际挠度、转角和扭角不应该超过许用挠度、转角和扭角。

主动轴的受力情况为弯扭组合情况，所以应该按弯扭合成强度理论计算，具体可以采用第三强度理论来进行计算。危险截面上当量应力计算如式（36）：

使其小于主动轴许用的弯曲应力。许用应力应取静应力状态下，铸钢的许用弯曲应力，此处取40 MPa，约束条件如式（37）：

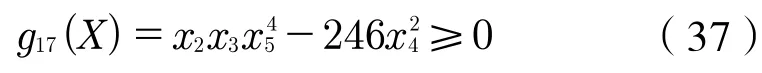
接下来列写刚度约束。轴的许用变形量可以根据机械设计手册查询，本文中，仅对轴的许用挠度进行约束即可。对于一般用途的轴而言，许用挠度一般为轴长度的0.000 3~0.000 5倍，在此取0.000 4，故主动轴刚度约束条件为：

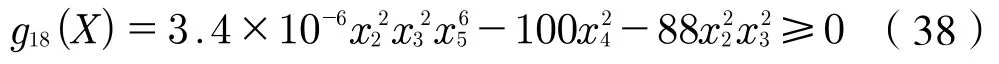
到此，已经成功地将优化问题转化为数学模型。

3 有约束单目标优化问题方案的选取

经过分析可知本文为一个有约束单目标优化问题，选用内点罚函数法进行求解[10]。

内点罚函数法属于罚函数法的一种。罚函数法的基本思想就是用所有的约束条件构造一个制约函数，当约束条件不满足时，该函数就会受到制约。反之，当约束条件满足时，则不受到制约。内点罚函数法要求迭代过程均在可行域内进行，在可行域的边界上设置制约，使得迭代点靠近边界时给出的函数值很大；距离边界较远的可行域内，约束函数几乎不起作用。因此，惩罚函数法构造的形式如下所示：

可以看出当函数接近边界点上时，罚函数接近无穷大，相当于在边界上设置了一道障碍，使得迭代过程不得超越出去，所以内点法也称障碍函数法[11-12]。

式中的rk称为惩罚因子，是递减的正数序列。由此可见，在迭代过程中惩罚因子逐渐减小，相当于目标函数中的惩罚项的作用越来越小，函数的最优点也会逐渐靠近可行域的边界，当惩罚因子等于0时，就得到原问题的最优解。

此处，利用Matlab编写相应内点罚函数法的迭代程序，并且进行求解。初始点应用原本减速器的六个设计变量取值，分别为[100 32 6 420 120 160]；c取0.5；ε取10-4；r0取1。将数据带入Matlab程序中进行计算。在对构造得到的内点罚函数进行无约束优化时发现，若利用罚函数分别对六个设计变量求一阶导数再联立方程组求解时间花费较长，运行一次r值大约需要1.5 h时间；故在此处选用牛顿法进行罚函数的无约束优化的最优点求解[13]。

经过大致1 h，结果矩阵求解得到。将六个设计变量、目标函数值和改进率计算，结果如表2所示。